Dauw en rijp nu stijgen niet tot de hoogste lucht, ook al is de lucht daar dichter, omdat de lucht bij de Aarde dan dichter is dan de middenlucht, om de genoemde redenen. Zodra dauw dus de middenlucht bereikt, kan hij niet opstijgen wegens de dunheid van de lucht ter plaatse (en deze plaats is niet in het midden van de lucht volgens Aristoteles*), maar lucht midden tussen de wolken en de Aarde), want warmte bereikt die in de nacht en de weerkaatsing van koude is bij de Aarde groter dan op die plaats.
Over deze opstijging door dichtheid en dunheid is hetzelfde te denken als over zoet en zout water°). De hoogste lucht kan namelijk vergeleken worden met zout water, de lagere met zoet water. En de lagere is zeer veranderlijk wegens weerkaatsing van de verschillende krachten van sterren en dampen, niet de vermengingen, maar de krachten: vermenging doet immers niets om een ding te steunen, tenzij iets zo met een vloeibaar lichaam vermengd wordt, als zout met water.
Den 2en Junij, in Noordtgouw.#) [<,>]
*) Meteorol. I, 3 en 4 (dauw en rijp: 10). Vergelijk Kepler, Ad Vitellionem Paralip., 129 (1604) en Epitome Astr. Copern., I, pars 3, 74 (1618). [Beeckman over de drie luchtlagen: II, p. 3.]
°) Vergelijk p. 289 en 292.
#) Afgezien van enkele onderbrekingen (p. 314, 322, 329) lijkt het verblijf van Beeckman bij zijn zwager Jacques Schouten [<] geduurd te hebben tot eind juli (p. 333).
Orgelpijpen
Waarom grotere buizen zwaardere geluiden geven en hoe dit gebeurt.Van klinkende pijpen geven grotere buizen zwaardere geluiden, zodanig dat die, welke tweemaal zoveel ruimte hebben, een octaaf lager klinken. Zo zijn twee buizen, waarvan de ene twee maten water bevat, en de andere drie maten van dezelfde inhoud*), een kwint van elkaar af en laat de kleinste buis een klank horen die een kwint scherper is dan de klank van de grootste buis.
Maar hoe worden buizen overeenkomstig met de verdelingen van muzikale samenklanken?
De reden hiervan is deze. Als de buizen leeg waren, zou een grotere niet verschillen van een kleinere in zwaarte, omdat het blazen, dat uit de mond komt, altijd van dezelfde soort zou zijn, en de snede bij de opening van de buizen steeds gelijk en dezelfde: deeltjes en bolletjes, dat wil zeggen van dezelfde grootte, zouden overal door de snede worden gekliefd.#)
Nu echter, terwijl de buizen vol lucht zijn, is het noodzakelijk dat deze door het blazen verwijderd wordt; en daar dit gelijk is, wordt de lucht des te moeilijker verwijderd naarmate hij zwaarder is, op de manier waarop water in grotere buizen zwaarder is dan in kleinere buizen.
Toch verschilt deze verwijdering van de zwaarte van water dat ergens op ligt, omdat water, hoe groot ook, op eenzelfde bodem°) liggend, van dezelfde zwaarte is op die bodem, wat komt omdat het water slechts ligt op de bodem; bij blazen door buizen moet echter lucht worden verwijderd. Aldus namelijk, als in de buizen water verwijderd zou moeten worden, zou ook zijn zwaarte veranderen naar de grootte van de buizen, omdat dan de bodem zou veranderen, of liever:
 [ *) Niet de inhoud, maar de lengte bepaalt de toonhoogte, zie Voetmaat in 'Register (orgel)'.]
[ *) Niet de inhoud, maar de lengte bepaalt de toonhoogte, zie Voetmaat in 'Register (orgel)'.][ #) Zie figuur: labiaalpijpen van metaal en van hout.
Het 'labium' bestaat uit twee delen: d, e (lower lip, upper lip); de lucht wordt van onder geblazen door de 'kernspleet' tussen c en d, en wordt dan gekliefd door het bovenlabium; hierbij ontstaan wervelingen en komt de lange luchtkolom tot een staande golf.]
°) Zie over de hydrostatische paradox: p. 48n; 73n; 75-76 en 108.
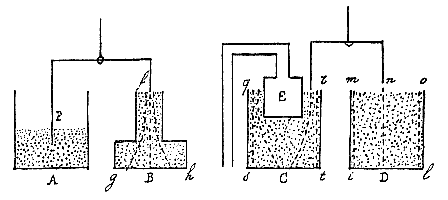


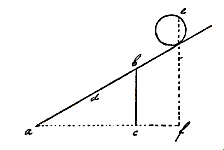 Bij voorbeeld: het stijgt veel langzamer door een buis ab dan door een buis cb, op geheel dezelfde manier als een steen sneller valt langs bc dan langs ab.
Bij voorbeeld: het stijgt veel langzamer door een buis ab dan door een buis cb, op geheel dezelfde manier als een steen sneller valt langs bc dan langs ab. 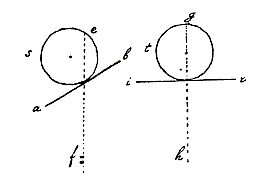 De reden waarom een steen s op een schuine lijn ab niet zo zwaar is, is de volgende. Alle atomen in de steen worden door de Aarde naar beneden getrokken, maar in de steen t loodrecht op gh, die door het contactpunt gaat, gaat deze lijn ook door het zwaartepunt van de steen en daarom beweegt hij naar geen van beide kanten, omdat ir evenwijdig is met de horizon, en daarom wordt de helft van de steen naar links getrokken, de andere helft naar rechts, dus blijft hij in rust.
De reden waarom een steen s op een schuine lijn ab niet zo zwaar is, is de volgende. Alle atomen in de steen worden door de Aarde naar beneden getrokken, maar in de steen t loodrecht op gh, die door het contactpunt gaat, gaat deze lijn ook door het zwaartepunt van de steen en daarom beweegt hij naar geen van beide kanten, omdat ir evenwijdig is met de horizon, en daarom wordt de helft van de steen naar links getrokken, de andere helft naar rechts, dus blijft hij in rust. 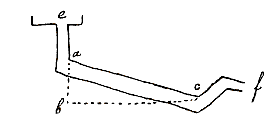 De buizen zijn twee duim breed en ze dalen zodanig, dat de buizen zich ten opzichte van de horizontale lijn verhouden als ac tot bc; en laat de hoogte zijn be. Als je dan ziet dat alle lucht die tussen a en c zit, weggaat via f, en dat niets van de lucht via e weer opborrelt, zal het mogelijk zijn zulke buizen, hoe lang ook, zo aan te leggen dat, als ac 10 voet is, en bc 8, dat dan ac ook 1000 voet zou kunnen zijn en bc 800, met inachtneming van dezelfde verhouding. De hoogte boven de schuine buizen moet dezelfde zijn als ae, maar de hoogte ab varieert met de lengte van de weg. [
De buizen zijn twee duim breed en ze dalen zodanig, dat de buizen zich ten opzichte van de horizontale lijn verhouden als ac tot bc; en laat de hoogte zijn be. Als je dan ziet dat alle lucht die tussen a en c zit, weggaat via f, en dat niets van de lucht via e weer opborrelt, zal het mogelijk zijn zulke buizen, hoe lang ook, zo aan te leggen dat, als ac 10 voet is, en bc 8, dat dan ac ook 1000 voet zou kunnen zijn en bc 800, met inachtneming van dezelfde verhouding. De hoogte boven de schuine buizen moet dezelfde zijn als ae, maar de hoogte ab varieert met de lengte van de weg. [