Hoeveel een steen, vallend in vacuüm, in de richting van het middelpunt van de Aarde, per afzonderlijk moment groeit in beweging, redenering van Descartes.   Op de voorgelegde vraag, waarbij men zich voorstelt dat in afzonderlijke tijden een nieuwe kracht wordt toegevoegd waarmee het zware lichaam omlaag gaat, zeg ik dat deze kracht op dezelfde manier vergroot wordt als de dwarsliggende lijnstukken de, fg, hi, en oneindig veel andere dwarsliggende lijnstukken, die men zich ertussen kan voorstellen.*) 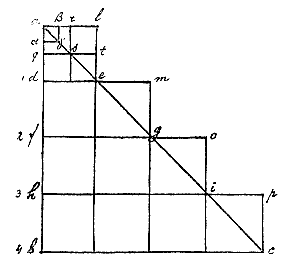  Laat ik, om dit aan te tonen, aannemen voor het eerste minimum of punt van beweging, dat veroorzaakt wordt door de eerste aantrekkende kracht van de Aarde die men zich kan voorstellen, het vierkant alde °). Voor het tweede minimum van beweging krijgen we het dubbele, namelijk dmgf: de kracht immers die er bij het eerste minimum was gaat door, en een andere nieuwe komt daarbij die gelijk is. Evenzo zullen er in het derde minimum van beweging drie krachten zijn, namelijk van het eerste, tweede en derde minimum van tijd, enz. En dit aantal is driehoekig, zoals ik elders zonodig uitgebreider zal uitleggen, en het blijkt deze driehoekige figuur abc te maken.   Integendeel, zult u zeggen, er zijn delen ale, emg, goi, etc., die uitsteken buiten de driehoekvorm; dus met die driehoekvorm moet deze reeks niet uitgelegd worden.   Maar ik antwoord dat die uitstekende delen daaruit voortkomen dat we een breedte gegeven hebben aan de minima, die we ons ondeelbaar moeten voorstellen, en niet uit delen bestaand. Wat als volgt wordt aangetoond:   Laat ik dat minimum ad verdelen in twee gelijke, in q; en nu is arsq <het eerste> minimum van beweging, en qted het tweede minimum van beweging, waarin twee minima zullen zijn van de krachten. Laten we op dezelfde manier verdelen df, fh, enz. Dan hebben we de uitstekende delen ars, ste, enz. Ze zijn kleiner dan het uitstekende deel ale, zoals blijkt. En als ik voor het kleinste weer een kleinere neem, zoals aα, zullen de uitstekende delen nog kleiner zijn, zoals αβγ, enz. En als ik tenslotte voor dat minimum het werkelijke minimum neem, namelijk een punt, dan zullen die uitstekende delen er niet zijn, omdat ze niet geheel een punt kunnen zijn, zoals blijkt, maar slechts de helft van het minimum alde; en de helft van een punt is er niet.   *)  Terwijl Beeckman uitgaat van behoud van beweging [<] en het optellen van verkregen snelheden, gaat Descartes uit van het idee dat de kracht behouden wordt en dat deze op elk moment evenredig is met de snelheid.   °)  Anders dan bij Beeckman [<] is hier langs de vertikale as de doorlopen weg uitgezet, en de oppervlakte stelt voor de som van gemiddelde snelheden.

[ 51 ]

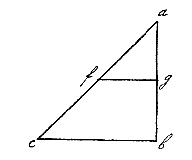Waaruit blijkt, als we ons bijvoorbeeld voorstellen dat de steen van a naar b getrokken wordt door de Aarde in vacuüm, met een kracht die er steeds gelijkmatig uit voortkomt, terwijl de vorige voortdurend blijft, dat de eerste beweging in a zich verhoudt tot de laatste die in b is, zoals punt a zich verhoudt tot het lijnstuk bc; en dat de helft gb door de steen driemaal zo snel doorlopen wordt als de andere helft ag, omdat hij met een driemaal zo grote kracht wordt aangetrokken door de Aarde: de ruimte fgbc is immers driemaal de ruimte afg, zoals gemakkelijk te bewijzen is. En hetzelfde is verhoudingsgewijs te zeggen over andere delen*).   En deze kwestie kan anders gesteld worden, en moeilijker, op de volgende manier: [<]   Laat men zich voorstellen dat de steen nog in het punt a blijft, met de ruimte tussen a en b vacuüm. En laat nu eerst, bijvoorbeeld vandaag het negende uur, God in b een kracht scheppen die de steen aantrekt, en daarna op afzondelijke momenten steeds een nieuwe, die gelijk is aan die welke hij in het eerste moment geschapen heeft. Deze wordt toegevoegd aan de eerder geschapen kracht, en trekt sterker aan de steen en weer sterker, omdat wat in vacuüm eenmaal beweegt, altijd beweegt [<]. En tenslotte komt de steen, die in a was, in b aan vandaag het tiende uur.   Als men vraagt in hoeveel tijd de eerste helft van de afstand afgelegd wordt, namelijk ag, en in hoeveel tijd de rest, antwoord ik dat de steen gedaald is over het lijnstuk ag in een tijd van 7/8 uur, en over de afstand gb in 1/8 uur. Dan moet namelijk een piramide gemaakt worden op driehoekige basis, waarvan de hoogte ab is, die op welke manier dan ook te verdelen is, samen met de gehele piramide, door middel van dwarsliggende lijnen even ver van de horizon. De steen zal des te sneller de onderste delen van lijnstuk ab doorlopen, naarmate de doorsnijdingen van de hele piramide groter zijn°).   Tenslotte kan het anders gesteld worden als met samengestelde interest [<]. Als men zich voorstelt dat deze op elk moment toeneemt, en als gevraagd wordt wat er verschuldigd is op het ene of andere tijdstip, wordt deze kwestie ook opgelost met verhoudingen afgeleid van een driehoek. Maar het lijnstuk ab moet niet verdeeld worden in rekenkundige delen, dat is gelijke, maar in meetkundige, of evenredige delen. Dit alles zou ik het duidelijkst kunnen bewijzen met mijn meetkundige Algebra, maar dit zou te ver voeren.   *)  Descartes bleef de snelheid zien als functie van de afstand (Beeckman: van de tijd), ook in zijn brieven van 1629.   °)  Dan zou dus de snelheid [?] toenemen met de derde macht en niet met het kwadraat. [ Als de kracht evenredig is met de tijd, is de versnelling het ook, dan wordt de afgelegde weg evenredig met de derde macht van de tijd, i.p.v. met het kwadraat, zie Eenparig versnelde beweging.]

[ 52 ]

Hydrostatische paradox   Tijdens hun ontmoetingen vroeg Beeckman aan Descartes de hydrostatische paradox aan te tonen, die al uitgelegd was door Stevin [<], en bekend aan Beeckman [<]. Onderstaand stuk was het resultaat, ook genoemd in 'Parnassus' [<]. Beeckman vermeldde het in 1619 [<], en liet het kopiëren omstreeks 1628. Redenering over samendrukkend water in een vat gegeven door de heer Descartes.   Om duidelijk mijn gedachten uiteen te zetten over de voorgelegde kwesties, zou ik veel van mijn grondslagen van de Mechanica vooraf moeten laten gaan, maar omdat de tijd het niet toelaat zal ik proberen ze kort uit te leggen, voorzover nu mogelijk is.   En ten eerste wel:  bij de verschillende manieren van zwaar zijn, die nu niet allemaal opgenoemd behoeven te worden, zijn er hier twee verschillende te onderscheiden, namelijk hoe water in een vat drukt op de bodem van dit vat, en hoe dit hele vat zwaar is, tegelijk met het water dat erin is. Die twee zijn namelijk geheel verschillend, zodat het zeker is dat het ene meer of minder zwaar kan zijn dan het andere.   Ten tweede:  om te begrijpen wat de uitdrukking zwaar zijn betekent, moet men zich voorstellen dat een lichaam, waarvan gezegd wordt dat het zwaar is, omlaag beweegt, en dit moet beschouwd worden op het eerste ogenblik van beweging. De kracht namelijk waardoor in het eerste ogenblik de beweging wordt aangezet, die is het die gravitatie genoemd wordt, niet die welke het tijdens de gehele beweging omlaag brengt, die zeer verschillend kan zijn van de eerste. We zullen dus zeggen dat gravitatie de kracht is waarmee het oppervlak dat het dichtst onder het zware lichaam ligt, erdoor naar beneden gedrukt wordt.   Ten derde:  bij die denkbeeldige oorsprong van beweging moet ook gelet worden op het denkbeeldige begin van snelheid, waarmee delen van het zware lichaam dalen; deze levert immers evenzeer een bijdrage aan het zwaar zijn als de omvang van het lichaam zelf. Bijvoorbeeld, als het ene wateratoom tweemaal zo snel daalt als twee andere atomen, zal dit op zijn eentje evenveel zwaarte geven als de twee andere.   Met deze vooronderstellingen nemen we vier vaten, van dezelfde breedte op de bodem, van hetzelfde gewicht als ze leeg zijn, en van dezelfde hoogte. In A wordt niet meer water gegoten dan B kan bevatten; de overige drie worden gevuld voorzover mogelijk.   Ten eerste zal het water samen met vat A evenveel zwaarte hebben als het water samen met B.   Ten tweede zal het water alleen op de bodem van vat B evenveel zwaarte hebben als het water alleen op de bodem van vat D, en dientengevolge meer dan het water op de bodem van vat A; eveneens gelijk aan het water op de bodem van vat C.

[ 53 ]

Compendium Musicae   Descartes gaf zijn 'Samenvatting van de Muziektheorie' als nieuwjaarsgeschenk voor 1619*) aan Beeckman [<]. Deze liet het later kopiëren, en hij nam het op in zijn 'boek'. De kopiist (dezelfde als van de vorige stukken) liet de achternaam weg, terwijl Beeckman geschreven had [<] deze juist via dit geschrift vernomen te hebben; deze vulde dan ook aan: Du Peron of Des Chartes. De tekst is elders beschikbaar°), en hier volgt alleen het eind, dat van persoonlijke aard is: het stuk was niet voor andere ogen bedoeld.   *)  Beeckman schijnt in het bezit van het stuk geweest te zijn toen hij Breda verliet op 2 jan. 1619 [<]. In elk geval schreef hij in zijn brief aan Mersenne van 1 oktober 1629 [>]: "De heer Descartes, onze vriend, in zijn boekje dat hij over de Muziek geschreven had en mij toezond ...".   °)  Cf. I, p. xxxviii met noot 2.  [1650;  Ned. 1661;  Fr: 1668;  txt AT.] Musicae Compendium des Cartes   [...]   En ik zie al land, ik haast me naar de kust; en veel laat ik hier weg door het streven naar kortheid, veel door vergeetachtigheid, maar zeker het meeste door onwetendheid. Ik laat toch toe dat deze boreling van mijn talent zo misvormd en als het ware als een pas tevoorschijn gebracht berenjong, naar u gaat, opdat het een herinnering is aan onze vertrouwelijkheid, en het zekerste aandenken van mijn liefde voor u: evenwel op deze voorwaarde alstublieft, dat het voortdurend in de schuilplaatsen van uw boekenkasten of studeerkamer verborgen blijft, en niet aan het oordeel van anderen onderworpen wordt. Zij zouden niet, zoals ik me voorhoud dat u wel zult doen, van verminkte delen hiervan de welwillende ogen afwenden naar die, waarin ik de omtrekken van mijn talent, naar het leven weergegeven, zeker niet verpest; en ze zouden niet weten dat het hier onder het onwetende soldatenvolk door een lui en vrijmoedig man, die verschillende dingen diep doordenkt en behandelt, in haast ter wille van u alleen is opgesteld.   Te Breda in Brabant, 31 december, aan het eind van het jaar 1618. Brieven René Descartes te Breda, aan Isaac Beeckman, te Middelburg. 24 januari 1619. *)   Uw brief °) was voor mij èn welkom èn verwacht, en bij de eerste blik was ik blij toen ik muzieknoten zag: hoe kon u immers ook duidelijker tonen dat u aan mij denkt? En er is iets anders dat ik ook met verwachtte, en vooral wat u gedaan hebt, wat u doet, hoe het met u gaat. En u hebt moeten geloven dat niet alleen de wetenschap mij ter harte gaat, maar ook u zelf; en niet alleen het verstand, ook al is dit het belangrijkste deel, maar de hele mens.   Wat mij aangaat, lui zoals ik ben, heb ik nauwelijks een titel gegeven aan de boeken die ik op uw aanraden ga schrijven. En toch u moet niet denken dat ik zo lui ben dat ik de tijd geheel nutteloos verslijt; ja zelfs nuttiger dan ooit, maar met zaken die uw verstand, bezig met hogere zaken, zonder twijfel zal geringschatten en waarop het vanuit de hoge hemel der wetenschappen zal neerzien, en wel met schilderkunst, militaire bouwkunde en vooral de Nederlandse taal, waarvan u binnenkort zult zien welke vorderingen ik erin gemaakt heb; ik zal namelijk naar Middelburg gaan, als God het toelaat, op de veertiende van de volgende maand.+)   *)  Journal, fol. 287v. [Ook bij www.chmtl.indiana.edu, evenals: Descartes aan Beeckman van 26 maart, 20, 23 et 29 april 1619; Beeckman aan Descartes, 6 mei 1619.]   °)  Verloren gegane brief van Beeckman, zoals de andere die hij aan Descartes schreef. Zie over Descaartes' Musica: T. I, p. 269.   +)  Aswoensdag viel dat jaar op 14 febr. Niet gebleken is dat het plan van Descartes is uitgevoerd; wel is op te merken dat we geen brieven hebben tussen 24 jan. en 26 maart 1619. [ Misschien had Descartes 14 maart in gedachten; de reis schijnt wel gemaakt te zijn, zie 26 maart: "die ik u bij mijn vertrek niet heb kunnen aanbieden. Zes dagen geleden ben ik hier teruggekomen" en: "naar Vlissingen ... bij het weggaan uit Middelburg". T. 1, p. XII: Descartes trof Beeckman niet aan in Middelburg. Op p. 280 een notitie van 2 maart, ook een van 7 maart (zonder plaats); na "De schippers seggen" volgt: Dordrecht, 22 maart; Rotterdam, 25 maart; p. 282: Leiden; en p. 283: Middelburg, 2 april.]

[ 57 ]

René Descartes te Breda, aan Isaac Beeckman, te Middelburg. 26 maart 1619.   Ik zal tenminste, denk ik, per brief de groet kunnen sturen, die ik u bij mijn vertrek niet heb kunnen aanbieden. Zes dagen geleden ben ik hier teruggekomen, waar ik mijn Muzen zorgvuldiger heb vereerd dan ooit tevoren. In zo korte tijd heb ik namelijk vier buitengewone en geheel nieuwe bewijzen gevonden, met behulp van mijn passers. Enige algebra van Descartes.   Het eerste is het zeer bekende over het verdelen van een hoek in een aantal gelijke delen.

[ 59 ]

Drie andere hebben betrekking op derdemachtsvergelijkingen, waarvan de eerste soort is tussen een absoluut getal, wartels en derde machten, de tweede tussen een absoluut getal kwadraten en derde machten, de derde tenslotte tussen een absoluut getal, wortels, kwadraten en derde machten. Hiervoor heb ik drie bewijzen gevonden, waarvan elk uit te breiden is tot de verschillende leden door verandering van de tekens + en −. Die heb ik nog niet allemaal onderzocht, maar ik zal gemakkelijk, naar ik meen, dat wat ik in het ene heb gevonden kunnen toepassen op de andere. En met deze wetenschap zullen viermaal zoveel en veel moeilijkere vragen kunnen worden opgelost, dan met de gewone Algebra; ik tel namelijk dertien verschillende soorten derdemachts­vergelijkingen*), zoals er slechts drie zijn van de gewone vergelijkingen, namelijk tussen  1 en  o + o N,  of  o − o N,  of tenslotte  o N − o.°) Iets anders is wat ik nu zoek over wortels die tegelijk getrokken moeten worden uit wat samengesteld is met meer verschillende namen +), omdat, als ik het zal vinden, zoals ik hoop, ik die wetenschap geheel op orde kan krijgen, als ik de ingeboren luiheid kan overwinnen en het lot me een vrij leven gunt.   *)  Het gaat om de vergelijkingen: ± a ± bx = x3,  ± a ± bx2 = x3  et  ± a ± bx ± cx2 = x3,  waarin a, b, c positieve grootheden zijn. Er zijn 16 combinaties van + et − mogelijk. Uitgezonderd moeten worden:  −a − bx = x3,  −a − bx2 = x3  en  −a − bx − cx2 = x3  die geen positieve wortel hebben.   °)  Voor de 'cossische' tekens, zie, T. 1, p. 5-6. Het gaat hier over vergelijkingen van de 2e graad: x2 = ax + b,  x2 = ax − b  en  x2 = b − ax,  waaraan hij niet toevoegt  x2 = −ax − b,  aangezien deze negatieve of imaginaire wortels heeft en bijgevolg beschouwd werd als onmogelijk.   +)  Het gaat om veeltermen van de vorm  a + √b + √c + .... Algemene wetenschap gezocht om alle vragen op te lossen.   En zeker, om u zonder meer te onthullen wat ik van plan ben, niet de Ars brevis van Llull*), maar een geheel nieuwe wetenschap wens ik te leveren, waarmee in het algemeen alle vragen zijn op te lossen die bij elke soort grootheid, zowel continu als discreet, kunnen worden voorgelegd. Maar elk naar zijn aard: zoals immers in de Rekenkunde sommige vragen met rationale getallen worden afgehandeld, andere alleen met onbevattelijke°), andere tenslotte wel bedacht kunnen worden, maar niet opgelost, zo hoop ik te zullen aantonen dat bij een continue grootheid sommige problemen kunnen worden opgelost met alleen rechte lijnen of cirkels. En dat andere alleen opgelost kunnen worden met andere kromme lijnen, maar die ontstaan uit een enkele beweging, en daarom met nieuwe passers getrokken kunnen worden, die ik voor even zeker en meetkundig houd als de gewone, waarmee cirkels worden getrokken. Tenslotte dat andere problemen alleen kunnen worden opgelost met kromme lijnen, voortgebracht met verschillende bewegingen die niet van elkaar afhankelijk zijn, die zeker slechts denkbeeldig zijn: de quadratrix is zo'n lijn, een vrij bekende. En ik denk dat er niets bedacht kan worden, dat niet tenminste met zulke lijnen kan worden opgelost, maar ik hoop dat het zo zal zijn dat ik bewijs welke soort vragen zijn op te lossen   *)  Raymond Lulle [Llull] (ca. 1232-1315) dacht een logische methode te hebben ontdekt, die hij scientia generalis noemde, en die de gemeenschappelijke ideologie van de scholastici zou vervolmaken. Zijn automatische bewerkingen trokken de aandacht van allen die de filosofie wilden opbouwen volgens een deductieve en wiskundige methode. Zie hierna p. 63 en 64-65.   [ °)  Irrationale of onmeetbare getallen. Lat. surdus (zie 'surd' in nth root). Stevin, L'Arithmetique (1585), p. 33: "racine quelconque est nombre", elke wortel is een getal.]

[ 60 ]

op deze of die manier en niet op de andere manier, zodat er vrijwel niets in de Meetkunde overblijft om uit te vinden. Het is wel eindeloos veel werk, en niet van één persoon. Ongelooflijk hoe ambitieus, maar ik weet niet wat voor licht ik heb gezien door de duistere chaos van deze wetenschap, met behulp waarvan alle dichtste duisternis uit de weg geruimd kan worden, denk ik. Voorgenomen reis van Descartes.   Wat betreft mijn reizen, die van kort geleden was gelukkig, en des te gelukkiger naarmate hij gevaarlijker was, vooral bij het vertrek van uw eiland. Want de eerste dag ben ik naar Vlissingen teruggegaan, door winden gedwongen; en de volgende dag, ingescheept op een heel klein bootje, heb ik een nog meer stormachtige zee ervaren, en toch met meer plezier dan angst. Ik heb namelijk mezelf op de proef gesteld, en na de zeegolven, die ik nooit eerder had beproefd, te zijn overgestoken zonder zeeziekte, ben ik moediger geworden om aan een grotere reis te beginnen. En de plotselinge roering in Duitsland heeft mijn plan niet gewijzigd, maar zorgt wel voor enige vertraging.*) Ik zal namelijk niet binnen drie weken hier vandaan vertrekken, maar ik hoop dat ik dan Amsterdam zal bezoeken, daar vandaan naar Danzig, daarna zal ik door Polen en een deel van Hongarije naar Oostenrijk en Bohemen gaan, welke weg zeker heel lang is, maar mijns inziens de veiligste. Bovendien neem ik mijn bediende mee en misschien metgezellen die mij bekend zijn. Ik schrijf dit opdat u niet bezorgd bent over mij, omdat u me waardeert. Doch ik zal zeker niet voor de vijftiende april hier vandaan vertrekken. U zult zelf bezien of ik voor die tijd een brief van u kan krijgen; anders zal ik die immers een lange tijd niet ontvangen. Maar als u schrijft, stuur dan wat u vindt van mijn Mechanica en of u het met mij eens bent.   *)  ... [Oeuvres, T. X (1908), p. 158n: Keizer Matthias was kinderloos overleden op 20 maart 1619.] "Oost ende West te seylen" door Descartes uitgevonden.   Bij het weggaan uit Middelburg heb ik nagedacht over uw navigatiekunde [<], en ik heb inderdaad een manier gevonden waarmee ik, overal ter wereld waar ik heen gevoerd zou worden, ook slapend en zonder kennis van de tijdens mijn reis verstreken tijd, door alleen naar de sterren te kijken, te weten zou kunnen komen hoeveel graden naar het Oosten of Westen ik verwijderd zou zijn van een ander gebied dat mij bekend is. Het is echter een niet zo vernuftige uitvinding, en daarom kan ik me moeilijk voorstellen dat ze tot nu toe door niemand is bedacht, maar ik zou veeleer menen dat ze veronachtzaamd is wegens de moeilijkheid in het gebruik. Op daartoe bruikbare instrumenten is één graad

[ 61 ]

niet groter dan twee minuten op andere instrumenten, voor het vinden van de poolshoogte; en daarom kunnen ze niet zo nauwkeurig zijn, terwijl Astrologen toch ook minuten en seconden, en nog kleinere delen, meten met hun instrumenten. Het zou me inderdaad verbazen, als zo'n uitvinding voor zeevaarders onbruikbaar zou lijken, waarbij zich geen ander nadeel voordoet. En daarom zou ik nauwkeuriger willen weten of er niet iets dergelijks is uitgevonden; en als u het weet, schrijf het me: ik zou namelijk deze overdenking, die nog verward in mijn hoofd zit, verder ontwikkelen, als ik zou vermoeden dat ze even nieuw is als zeker.   Blijf mij ondertussen genegen, leef gelukkig en het ga u goed. U zult nog een brief van me ontvangen voor mijn vertrek.   Bredae Brab., 7o Kal. Aprilis. Tuus si suus    DU PERRON.   (het opschrift was:)     A Monsieur   Monsieur Isaac Beeckman Docteur en medecine, in de Twe Hanen by de Beestemarckt     à Middelburgh. René Descartes te Breda, aan Isaac Beeckman, te Middelbourg. 20 april 1619.   Ik heb deze bode niet naar u willen sturen zonder een brief, ook al heb ik nu geen tijd om veel te schrijven. Maar ik vraag alleen dat u mij via hem, die mijn bediende is, terugschrijft: hoe het met u gaat, en wat u doet, of u nog bezig bent met een bruiloft*), maar nu niet van een ander°)? Ik zal volgende woensdag +) hier vandaan vertrekken, meteen als de bode teruggekeerd is van u naar mij. Drie weken geleden heb ik meer geschreven.   Het ga u goed en wees mij genegen.   Bredae Brabant., 12 Kal. Maij 1619 Tuus aequè ac suus   DU PERRON     *)  Beeckman was half oktober naar Breda gekomen (zie T. 1, p. 228), ongetwijfeld om zijn uitverkoren meisje te ontmoeten, en Descartes lijkt het geweten te hebben. Nu dacht Beeckman in Middelburg aan een huwelijk. Maar hij vertrok in november 1619 naar Utrecht, tot zijn huwelijk, 20 april 1620 te Middelburg, met Cateline de Cerf. Het vermoeden van T. 1, p. X) lijkt bevestigd: dat het verblijf in Breda te maken had met zijn toekomstige vrouw.   °)  Ongetwijfeld het huwelijk van Jacob Beeckman (zie hierboven, p. 58). Beeckman lijkt veel bezig te zijn geweest met dit huwelijk van zijn broer.   +)  24 april 1619. Descartes vertrok op 29 april per schip uit Amsterdam (zie p. 64 hierna).

[ 62 ]

(het opschrift was:)     A Monsieur   Monsieur Isaac Beeckman, in de Twee Haenen by de Beestemarckt     à Middelb. René Descartes te Breda, aan Isaac Beeckman, te Middelburg. 23 april 1619.   Ik heb uw brief bijna op dezelfde dag ontvangen als waarop hij geschreven is, en ik wilde niet hier vandaan vertrekken zonder nog eenmaal per brief onze vriendschap te vernieuwen, die zal blijven bestaan. Toch moet u nu niet iets van onze Muzen verwachten; mijn hoofd is nu op reis, terwijl ik me aangord om morgen op weg te gaan. Ik ben nog onzeker waarheen het lot ons zou voeren en waar het vergund zou worden ons te vestigen.*) Want de oorlogsroeringen roepen me beslist nog niet naar Duitsland, en ik vermoed dat er wel veel mensen onder de wapenen zullen zijn, maar dat er geen slag zal zijn. Als dit zo is, zal ik intussen in Denemarken, Polen en Hongarije wandelen, totdat in Duitsland hetzij de route veiliger is en niet in beslag genomen door rovende soldaten, hetzij een oorlog voor mij met meer zekerheid te verkrijgen is.   Als ik ergens langer blijf, zoals ik hoop dat ik zal doen, beloof ik u dat ik terstond zal beginnen de Mechanica of de Meetkunde te ordenen, en ik zal u als bevorderaar van mijn studie en als eerste ontwerper opnemen. Descartes over mij.   U bent namelijk inderdaad de enige die een lui iemand als mij in beweging hebt gebracht, de geleerdheid die al bijna uit het geheugen geglipt was weer hebt opgeroepen, en het verstand dat van ernstige bezigheden afgedwaald was naar iets beters hebt teruggebracht. En als dan iets van mij uitgaat dat misschien niet van weinig betekenis te achten is, zult u dat met recht geheel voor u kunnen opeisen; en ik zal zelf niet nalaten het aan u te zenden, zowel om ervan te genieten, als om het te verbeteren. Oost ende West niet gevonden. Zoals zeer onlangs over wat ik aan u schreef over de scheepvaart, het is hetzelfde dat u, alsof u helderziend bent, aan mij hebt gestuurd: die vinding van u over de Maan is namelijk hetzelfde [<]. Waarvan ik echter meende dat het met instrumenten vergemakkelijkt zou kunnen worden, maar dat was een vergissing.   Dat, waarop ik me beroemde te hebben gevonden bij het andere dat hierboven staat, heb ik echt gevonden met nieuwe passers, en ik vergis me niet. Maar ik zal het niet stuk voor stuk aan u schrijven, omdat ik dit hele werk hierover een keer zal overdenken, mijns inziens is het nieuw, en niet van weinig betekenis te achten. Doch nu heb ik bijna een maand niet gestudeerd, omdat namelijk het verstand door die uitvindingen zo uitgeput was,   *)  Vergilius, Aen., Lib. III, 7. [Ned. van Ben Bijnsdorp.]

[ 63 ]

dat het niet voldoende was om andere dingen te vinden, die ik nog besloten had te onderzoeken. Doch het zal voldoende zijn om de herinnering aan u altijd te bewaren. Vale. 9o Kal. Maij 1619 Tuus aeque ac suus   DU PERRON.   (het opschrift was:)     A Monsieur   Monsieur Isaac Beecman, in de Twee Haenen, by de Beestemarckt,   à Middelborgh. René Descartes te Amsterdam, aan Isaac Beeckman, te Middelburg. 29 april 1619.   Ik wil geen enkele gelegenheid u te schrijven voorbij laten gaan, opdat ik datgene wat ik tot stand heb gebracht in verband met u en ook de herinnering laat zien, door geen bezigheden onderweg belemmerd. Wetenschap van Llull.   Eergisteren heb ik een geleerd iemand gevonden in een Dordrechtse herberg, met wie ik heb gesproken over de Ars parva*) van Llull: hij beroemde zich erop deze te kunnen gebruiken, en wel met zoveel succes dat hij over welke materie dan ook een uur met praten zou kunnen vullen, en vervolgens, als hij nog een uur over dezelfde zaak zou handelen, heel andere dingen dan de voorgaande zou vinden, en zo twintig uur achtereen. Of u het kunt geloven, zult u zelf gezien hebben. Het was een oude man, een beetje spraakzaam, en wiens eruditie, kennelijk uit boeken gehaald, veeleer op het puntje van zijn tong zat dan in de hersenen.   En ik vroeg nauwkeuriger of die wetenschap niet bestond in enige volgorde van dialectische onderwerpen, waaraan redeneringen worden ontleend; en hij zei van wel, maar voegde er bovendien aan toe dat noch Llull noch Agrippa°) in hun boeken enige sleutels hebben geleverd, die noodzakelijk zijn, naar hij zei, om de geheimen van die wetenschap toegankelijk te maken. Dat heeft hij zeker gezegd, vermoed ik, om bewondering te krijgen van een onwetende, veeleer dan overeenkomstig de waarheid te spreken.   Ik zou toch willen nagaan of ik het boek zou kunnen krijgen; maar daar u het hebt [>], als u tijd hebt, ga het dan na, alstublieft, en schrijf of u iets scherpzinnigs vindt in die wetenschap. Ik heb zoveel vertrouwen in uw verstand, dat ik er zeker van ben dat u makkelijk zult zien hoe die zijn, als ze er tenminste zijn,   *)  De Ars brevis, zie p. 59 hierboven, en T. I, p. 294.   °)  Het aantal Commentaren op de Ars generalis van Llull is groot, maar aan Io. Henr. Alstedius is te danken een Clavis artis Lullianae et verae Logicae (Argentorati, 1609), in-8o.

[ 64 ]

die weggelaten punten die noodzakelijk zijn om de andere te begrijpen, die hij sleutels noemt. En ik heb u dit willen schrijven, opdat ik nooit nalaat over uw geleerdheid te spreken, omdat u het verlangt. En als ik hetzelfde van u vraag, wilt u het dan alstublieft niet weigeren.   Vandaag scheep ik me in, om Denemarken te bezoeken, ik zal enige tijd in Kopenhagen zijn, waar ik een brief van u verwacht. Elke dag gaan hier namelijk schepen vandaan, en ook al kent u de naam van mijn gastheer niet, toch zal ik zo zorgvuldig zijn bij het vragen of zeevaarders een brief voor mij brengen, dat ze onderweg niet gemakkelijk verloren kunnen gaan. Zorg ervoor, alstublieft, dat mijn hier bijgevoegde brief terstond geleverd wordt aan Pieter van der Merckt*). Verder heb ik niets meer, behalve dat ik wil dat u mij genegen bent en dat u gelukkig bent.   Vale. Amsterodami, 29 Aprilis 1619. Tuus si suus DU PERRON. (het opschrift was:)     A Monsieur   Monsieur Beecman, Docteur en medecine     à Middelb. Isaac Beeckman, te Middelburg, aan René Descartes, te Kopenhagen. 6 mei 1619.   Ik heb uw brief ontvangen en de ingesloten brief heb ik afgeleverd aan Pieter van der Merckt*), zoals u aan mij had geschreven. En hoewel er niets is waarop ik u kan antwoorden, toch heb ik dit weinige toegevoegd, opdat u weet dat ik de uwe ontvangen heb. Wetenschap van Llull. U schrijft dat u in Dordrecht een geleerd man hebt gevonden, die u daarna toch niet geleerd wilt noemen om enkel de kennis van de wetenschap van Llull, waarop hij zich liet voorstaan. U vraagt me de Commentaren van Agrippa zorgvuldig door te nemen en de sleutels, zoals uw oude man ze noemde, er uit te vissen, waarmee die wetenschap toegankelijk wordt gemaakt door Agrippa of Llull zelf, niet aan deze wetenschap toegevoegd opdat niet iemand zo maar erin bedreven zou worden; u hebt namelijk zoveel vertrouwen in mijn verstand dat, als er iets in deze wetenschap is verborgen, het mij niet onbekend kan blijven wanneer ik me zorgvuldiger wil toeleggen op de Commentaren. En ik zou u zeker gehoorzamen, buitengewone vriend van mij, als gebrek aan tijd het niet zou verhinderen. Ik vrees namelijk dat u niet zo lang kunt blijven in   *)  Pieter van der Merckt ... (1587-1625), reder te Middelburg. Het gaat waarschijnlijk om een wisselbrief.

[ 65 ]

Kopenhagen, aangezien brieven onderweg vrij vaak blijven steken voordat ze op de plaats van bestemming aankomen.   Bovendien, tenzij me geheel ontvallen is wat ik een aantal jaren geleden over deze zaak had opgenomen uit een oppervlakkige lezing van deze Commentaren van Agrippa, deze lang gezochte sleutels zijn er niet; uit die Agrippa zou u ze immers zelf, als u het onlangs had gewild, precies hebben kunnen opmaken. Want alles wat er is, verdeelt hij in algemene plaatsen, en deze afzonderlijk verdeelt hij weer verder in andere, zodat er niets van een zaak bedacht kan worden dat niet bevat is in die cirkels [<], in het algemeen en in het bijzonder; tenslotte verbindt hij met letters de plaatsen van verschillende cirkels met elkaar. En zo, als een willekeurige zaak is voorgesteld, zal door combinatie van alle termen de tijd van opnoemen uitgerekt kunnen worden tot bijna oneindig veel uren; maar het is noodzakelijk dat degene die ze opnoemt van veel zaken op de hoogte is, en dat wie langer spreekt veel lachwekkends zal zeggen, en dingen die weinig ter zake doen, en tenslotte helemaal een fantast wordt en het hele geheugen zo volstopt met de lettertekens, dat hij nauwelijks geschikt is om iets wezenlijks te overdenken.   Dit zij genoeg over deze zaak, tenzij u nog iets anders wilt. God geve dat we enige tijd samen kunnen doorbrengen, om het wetenschappelijk strijdperk tot in het midden te betreden*). Let intussen op uw gezondheid, en wees verstandig op uw gehele reis, opdat u niet juist de beoefening van die wetenschap, waaraan u zoveel waarde hecht, lijkt te verwaarlozen. Vergeet niet mijn en uw Mechanica die moet worden beschreven; u bent immers gewend uw beloften nauwkeurig gestand te doen, vooral als u ze hebt opgeschreven. Och, had u daar ook maar tijd aan gegeven! U vertoeft nu in de belangrijkste stad van dat koninkrijk; zie erop toe dat er niet iets aan kennis is dat u niet onderzoekt, of een geleerd iemand die u niet bezoekt, opdat er niet iets goeds in Europa voor u verborgen blijft, of liever opdat u zich een voorstelling maakt van de verhouding van u tot andere geleerden. Met mij gaat het goed.   Pridie Nonarum Maij [6 mei] 1619, stylo novo.   Uit uw vaderland is een Fransman naar hier gekomen, iemand die in het openbaar de schoonste kunsten verkondigde, voortdurend springende bronnen van hetzelfde water, krijgskunde, geneeskunde, toename van de huishouding bij het vermenig­vuldigen van brood, terwijl hij zelf aan alles gebrek had. Deze heb ik gesproken en aan een onderzoek onderworpen; ik heb hem onwetend bevonden van bijna alle zaken, ook die welke hij verkondigde. Dus hier zal hij niets uitrichten en hij moet verwezen worden naar noordelijker streken, waar botte verstanden meer openstaan voor misleiding.°) Tuus ut suus       ISACK BEECKMAN (het opschrift was)     A Monsieur   Monsieur René Du Perron estant in Denemarcken     Coppenhaghen. port.   *)  De twee vrienden zouden elkaar pas weer ontmoeten in oktober 1628.   [ °)  Zie over dit postscriptum: Klaas van Berkel, Isaac Beeckman on Matter and Motion. Mechanical Philosophy in the Making, Baltimore 2013, p. 27:] Was this simply a nice story, or a warning disguised as a joke ... Or was this a fictional version of Beeckman's true impression of Descartes? Although it is hard to imagine that Beeckman meant it this way, Descartes would have viewed the story as an unexpected and painful rebuke by someone whom he regarded as a trusted friend. But ... we are not sure that Descartes actually received this letter, so further speculation is best left to others.   [ Het waren wel twee 'fantasten' bij elkaar, zie Beeckman over de tol, waarom deze rechtop blijft staan (T. 1, p. 242-243, nov. 1618), met de gedachte aan een bord, draaiend op de punt van een mes:   "sy en sal soo ras, al drayende, niet beneden syn alse van een solder valt, dan niet drayende." Descartes ging verder: misschien kan een mens zich zo in de lucht houden.]