Compendium Musicae
[ Descartes gaf zijn Compendium Musicae als nieuwjaarsgeschenk voor 1619 aan Beeckman [<]. Deze liet het later kopiëren, en hij nam het op in zijn 'boek'. De kopiist (dezelfde als van de vorige stukken) liet de achternaam weg, terwijl Beeckman geschreven had [<] deze juist via dit geschrift vernomen te hebben; deze vulde dan ook aan: Du Peron sive Des Chartes.
De tekst is elders beschikbaar°), en hier volgt alleen het eind, dat van persoonlijke aard is: het stuk was niet voor andere ogen bedoeld.]
Descartes offrit encore à Beeckman, pour ses étrennes de 1619, le Compendium Musicae qu'il avait composé à la fin de 1618*). Plus tard, vers 1626, Beeckman fit copier l'original par le copiste de la main gothique qui avait déjà transcrit les documents précédents et il l'inséra dans son Journal, où la copie occupe fol. 163recto - 178verso. Comme nous l'avons déjà remarqué le copiste avait mis en haut de la première page: René Isaco Beeckman, sans mentionner le nom de famille de l'auteur; en effet Beeckman avait appris ce nom précisément au moyen de cet écrit [<]. Aussi Beeckman ajouta-t-il avec un signe d'intercalation après René: Du Peron sive Des Chartes, et mit-il encore ensuite à la marge gauche: Musicae Compendium des Cartes.
En supprimant le texte de l'écrit dont on a plusieurs éditions°), nous reproduisons ici seulement la fin très personnelle.
*) Beeckman semble avoir été en possession de l'écrit lorsqu'il quitta Breda le 2 janvier 1619 [<]. Toutefois, il écrivit dans sa lettre à Mersenne du 1er octobre 1629 [>]: "D. des Chartes, amicus noster, in libello suo quem de Musica conscriptum ad me misit ...".
°) Cf. t. I, p. xxxviii avec la note 2. [www.chmtl.indiana.edu (txt AT); 1650, p. 57; Fr: 1668, fin.]
Musicae Compendium des Cartes
[...]
Jamque terram video, festino ad littus; multaque brevitatis studio, multa oblivione, sed plura certe ignorantiâ hîc omitto. Patior tamen hunc ingenij mei partum ita informem et quasi ursae foetum nuper editum, ad te exire, ut sit familiaritatis nostrae mnemosynon, et certissimum mei in te amoris monimentum: hac tamen, si placet, conditione, ut perpetuo in scriniorum vel Musaei tui umbraculis delitescens, aliorum judicia non perferat. Qui, sicut te facturum mihi polliceor, ab hujus truncis partibus benevolos oculos non diverterent ad illas, in quibus nonnulla certe ingenij mei lineamenta ad vivum expressa non inficior; nec scirent hic inter ignorantiam militarem ab homine desidioso et libero, penitusque diversa cogitante et agente, tumultuose tui solius gratiâ esse compositum.
Bredae Brabantinorum, pridie Calendas Ianuarias. Anno MDCXVIII completo.
[ Ned. (vert. J. H. Glazemaker, 1661), p. 45-6:]
|
Ik zie nu lant, en spoed my naar de strant. Ik sla veel over om kort te zijn, en veel uit vergetenheit, en noch meer uit onkunde. Ik lijd nochtans dat deze vrucht van mijn vernuft, dus wanstaltig, en gelijk het jong van een beer, onlangs geworpen, voor u verschijnt, op dat het een pant van onze vrientschap, en een zeer zeker gedenkteeken van mijn liefde tot u zou zijn, doch echter, zo 't u belieft, met deze voorwaarde, dat het, eeuwiglijk in de schaduw uwer koffers en kassen verborgen, d'oordelen van anderen niet behoeft uit te staan, die, gelijk ik vertrou dat gy doen zult, hun ogen niet jonstelijk van des zelfs kreupele of verminkte delen naar de genen zouden keren, in de welken (ik wil 't niet ontkennen) enige trekken van mijn vernuft naar 't leven uitgedrukt zijn, en die ook niet zouden weten dat het onder een oorlogsche onkunde van een onbekommert en ledig man, en die geheellijk iets anders denkt en doet, met 'er haast, en alleenlijk u te geval, gemaakt is.
|
Brieven
Journal, fol. 287v. *)
René Descartes à Breda, à Isaac Beeckman, à Middelbourg.
24 janvier 1619.
Et acceptae et expectatae mihi fuerunt tuae litterae°), gavisusque sum primo intuitu cum Musicae notas inspexi: quo enim pacto et memorem mei clarius ostenderes? Aliud autem est quod etiam expectabam et praecipue quid egeris, quid agas, ut valeas. Neque enim scientiam solam, sed te ipsum mihi curae esse debuisti credere; nec ingenium solum, etiamsi pars sit maxima, sed hominem totum.
Quod ad me pertinet, desidiosus meo more, vix titulum libris, quos te monente scripturus sum, imposui. Neque tamen me ita desidiosum existimes, ut plane tempus inutiliter conteram; imo nunquam utilius, sed in rebus quas ingenium tuum, altioribus occupatum, haud dubie contemnet et ex edito scientiarum coelo despiciet, nempe in pictura, architectura militari et praecipue sermone Belgico, in quo quid profecerim, brevi visurus es; petam enim Middelburgum, si Deus sinat, quadragesima ineunte.+)
[ *) Cf. www.chmtl.indiana.edu, aussi pour: Descartes à Beeckman de 26 mars, 20, 23 et 29 avril 1619; Beeckman à Descartes, 6 mai 1619.]
°) Lettre perdue de Beeckman, comme les autres qu'il écrivit à Descartes. Cf. t. I, p. 269 [Musica].
+) Le mercredi des cendres, premier jour du Carème, tomba cette année le 14 février. Il n'apparait pas que le projet de Descartes fut exécuté; toutefois il est bien remarquable que nous n'ayons pas de lettres échangées entre les deux amis pendant un assez long laps de temps (24 janvier-26 mars 1619).
[ 26 mars: "quod tibi discedens dicere non potui. Ante sex dies huc redij", "Vlessigam ... Middelburgo exiens".
T. 1, p. XII: "N'ayant pas trouvé Beeckman à Middelbourg, en mars 1619, - ce dernier étant alors à Dordrecht, à Rotterdam et à Leyde - Descartes prit congé de lui par des lettres datées d'avril 1619".
T. 1, p. 280: 2 mars, Middelburg; 7 mars (s.l.); p. 281: "De schippers seggen"; 22 mars, Dordrecht; 25 mars, Rotterdam; p. 282: Leiden; et p. 283: Middelburg, 2 avril.]
|
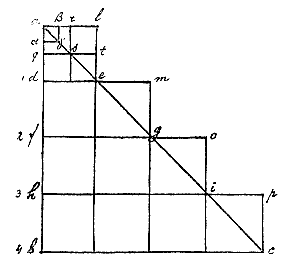 Quod ut demonstrem, assumam pro primo minimo vel puncto motûs, quod causatur a prima quae imaginari potest attractiva vi Terrae, quadratum alde °). Pro secundo minimo motus, habebimus duplum, nempe dmgf : pergit enim ea vis quae erat in primo minimo, et alia nova accedit illi aequalis. Item in tertio minimo motus erunt tres vires, nempe primi, secundi et tertij minimi temporis, etc. Hic autem numerus est triangularis, ut alias forte fusius explicabo, et apparet hunc figuram triangularem abc repraesentare.
Quod ut demonstrem, assumam pro primo minimo vel puncto motûs, quod causatur a prima quae imaginari potest attractiva vi Terrae, quadratum alde °). Pro secundo minimo motus, habebimus duplum, nempe dmgf : pergit enim ea vis quae erat in primo minimo, et alia nova accedit illi aequalis. Item in tertio minimo motus erunt tres vires, nempe primi, secundi et tertij minimi temporis, etc. Hic autem numerus est triangularis, ut alias forte fusius explicabo, et apparet hunc figuram triangularem abc repraesentare.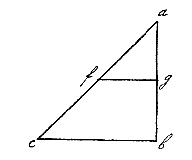 Ex quibus patet, si imaginetur, verbi gratia, lapis ex a ad b trahi a Terra in vacuo per vim quae aequaliter ab illa semper fluat, priori remanente, motum primum in a se habere ad ultimum qui est in b, ut punctum a se habet ad lineam bc; mediam vero partem gb triplo celerius pertransiri a lapide quam alia media pars ag, quia triplo majori vi a Terra trahitur: spatium enim fgbc triplum est spatij afg, ut facile probatur. Et sic proportione dicendum de caeteris partibus.*)
Ex quibus patet, si imaginetur, verbi gratia, lapis ex a ad b trahi a Terra in vacuo per vim quae aequaliter ab illa semper fluat, priori remanente, motum primum in a se habere ad ultimum qui est in b, ut punctum a se habet ad lineam bc; mediam vero partem gb triplo celerius pertransiri a lapide quam alia media pars ag, quia triplo majori vi a Terra trahitur: spatium enim fgbc triplum est spatij afg, ut facile probatur. Et sic proportione dicendum de caeteris partibus.*)