Drie kwarten
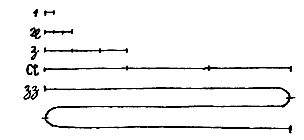
Reden van b dur, b mol en natuurlijk.* Drie soorten kwarten hebben aanleiding gegeven tot drie soorten gezang: b mol, het natuurlijke en b dur; de drie soorten zijn ut fa, re sol, mi la. [<]
De reden nu waarom ut fa genoemd wordt mol, is omdat in een toonladder van Guido, die loopt volgens b dur*), wanneer hij is aangekomen bij b, altijd gezongen wordt mi; maar wanneer daar in het hele gezang fa wordt gezongen, noemt men het gezang b mol. Dan wordt daar namelijk de eerste soort kwart ut fa gevormd; daar zeg ik, want op andere plaatsen van de toonladder wordt even goed ut fa herhaald als hier; en in een mol gezang wordt even goed b dur herhaald als in het genoemde dur gezang.
Ze worden dus niet zo genoemd omdat het ene harder is dan het andere, maar, zoals gezegd, omdat de fa op deze plaats gezet wordt, die daar niet werd gezet in het harde, slechts ter onderscheiding en verscheidenheid tussen de verschillende toonladders.
Waarom nu ut fa genoemd worden zoete noten, re sol natuurlijke, en mi la harde, hebben we elders gezegd [<]. Maar we zien een duidelijk verschil, omdat ut wordt voorgedragen als fa; deze heeft immers altijd een halve toon onder zich, terwijl ut die kan hebben. Verondersteld wordt te hebben, omdat er niets onder is, en bij diminuties van de spraak lijkt er altijd veeleer een halve dan een hele toon op te duiken, omdat de eerste het dichtst bij is en de terugkeer naar de noot ut daarom makkelijker is.
De mi heeft altijd een halve toon boven zich, waaraan de la gelijkend is, omdat die ook een halve toon boven zich kan hebben, ja zelfs altijd heeft, wanneer hij slechts één noot boven zich heeft, en dit opdat een grote kwart tegen de fa eronder vermeden wordt. De re noch de sol heeft noch onder, noch boven zich een halve toon, dus deze twee zijn gelijkend. Vandaar dat, zoals Maillart zegt [<], de kwart heel makkelijk is bij het zingen, dat wil zeggen dat we makkelijker ut fa voordragen dan ut sol.
Waarom nu ut fa genoemd wordt zoet, mi la hard enz. heb ik al eerder gevraagd of zal ik nog eens vragen.
Zo zijn dus noten op zich zoeter, het gezang toch niet, behalve met het oog op de verscheidenheid.
[ *) Symbool: de "vierkante" b die er eerder als een h uitziet (♮), nu ons herstellingsteken. Zie:
Nic. Listenius, Musica, 1537 ... (Engl., ed. Sion M. Honea, 2016), figuren: 'Scala ♮duralis' en 'Scala b mollaris', beide voor stijgen en dalen, links:"♮quadratum mi format", rechts: "b rotundum fa notat".]


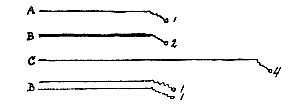
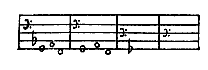 Want in de bas, zoals je hier ziet, kan gezongen worden de eerste, derde en vijfde toonsoort, die bij
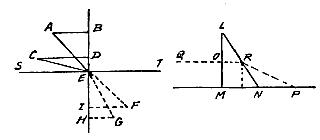
Want in de bas, zoals je hier ziet, kan gezongen worden de eerste, derde en vijfde toonsoort, die bij 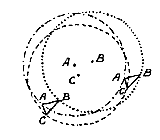 Laat driehoek ABC een bewegend lichaam zijn, dat beweegt om drie middelpunten A, B en C, dan zullen door de hoeken van de driehoek drie gelijke cirkels beschreven worden. En op elke plaats blijven dan alle lijnen evenwijdig aan elkaar, dat wil zeggen AB evenwijdig aan AB en AC evenwijdig aan Ac en BC evenwijdig aan BC.
Laat driehoek ABC een bewegend lichaam zijn, dat beweegt om drie middelpunten A, B en C, dan zullen door de hoeken van de driehoek drie gelijke cirkels beschreven worden. En op elke plaats blijven dan alle lijnen evenwijdig aan elkaar, dat wil zeggen AB evenwijdig aan AB en AC evenwijdig aan Ac en BC evenwijdig aan BC. 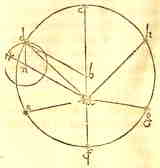
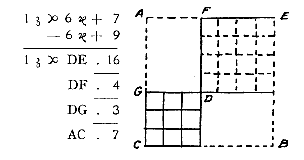
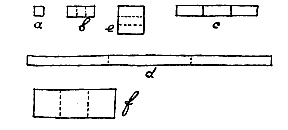 Hij vat de eenheid op als een klein vierkantje; zo vat hij ook een punt op°). En een lijn of wortel#) vat hij op als een rechthoek, opgebouwd met één zijde van dat vierkantje en de vereiste lengte.
Hij vat de eenheid op als een klein vierkantje; zo vat hij ook een punt op°). En een lijn of wortel#) vat hij op als een rechthoek, opgebouwd met één zijde van dat vierkantje en de vereiste lengte.