Isack Beeckman

Home | Beeckman | < Vertaling > | Brontekst | Index

Klein, verbeelding , tellurium , vacuüm , beweging , zwaar , druk , oneindig , geest , licht , geluid , spiegels

Isack Beeckman - 1613 v

[ < 17 ] [ nov. 1612 - maart 1613 ]

Wonderlijk klein
Hoe klein dingen zijn.
Verwonderlijk is de fijnheid van dingen in de dingen.
"Want een dinck in een man, dat maer een aesken en weecht, en weecht qualick het 2413^de deel van een aesken in een" voor het eerst gevormd kind.
"Denckt hoe kleyn dat moet syn, ende denckt, hoe kleyn dat is datter alle ure aenwast totdattet so groot is als in een volwassen man."
Zodat de mening van Anaxagoras: "Alle dingen zijn in alle dingen" niet wonderlijker lijkt te zijn.

Verbeelding
Verbeelding verbonden met een figuur.*)
Wanneer ik de maanden van het jaar beschouw, beschouw ik die alsof de winter, de zomer enz. rondom mij zou staan, als in een langwerpige cirkel, waarin de afzonderlijke gedeelten zijn geplaatst. En ik ga daarin zo ver, dat ik me elke maand in een ander gedeelte van de cirkel opstel. En ik kan niet anders over het jaar denken dan met zo'n hulpmiddel.
nummers bij gebogen lijn
Mijn verbeelding van getallen.
Evenzo wanneer ik getallen beschouw, kan ik niet anders dan de plaats ervan op deze manier te beschouwen, zodat de eenheid onderaan staat, en zo opstijgend naar rechts en naar links tot aan het midden.

Mijn verbeelding van beweging langs een spiraal.
Nog eens evenzo, bij het beschouwen van een vat dat men gebruikt bij het afkoelen van wijngeest°), waar binnenin pijpen of buisjes rondgaan in de vorm van een spiraal, en het onderste deel buiten het vat uitsteekt — ik zeg: als ik bedenk dat in die pijp een bolletje wordt losgelaten, dat door die pijp in het rond omlaag loopt, stel ik me die baan zo sterk voor^#) dat ik het niet naar wens kan onderdrukken, zodat ik kan denken dat het bolletje er uitspringt, maar door mij wordt erbij gedacht dat het bolletje voortdurend blijft ronddraaien, ook buiten de betreffende opening.
Wat dit kan bijdragen aan de 'pneumatologie' van onze geesten, kunnen de geleerden bekijken.

[ *) Zie: Mnemotechniek.]
[ °) Lat. 'spiritus vini' (alcohol), "voorloop van den gebranden Wyn", volgens Medicina pharmaceutica (1681), p. 88; figuur op p. 66: koper-ketel met de slange.]
[ ^#) Lat.: "adeo mei spiritus in gyrum aguntur", worden mijn geesten zo in een kringloop gebracht. Zie ook het gebruik van 'spiritus' op p. 28 hierna.
Met 'pneumatologie' zal bedoeld worden de theorie van Erasistratos en Galenus over een 'pneuma psychikon', zie:
C. U. M. Smith, The Problem of Life: An Essay in the Origins of Biological Thought (1976), p. 105-111, m.n. 110.]

[ Ned. ]

[ 21 ] [ juli 1613 - april 1614 ]

Wandelende steen
Steen die rondwandelt in azijn.

Ik heb een witachtige steen in azijn zien rondwandelen, in Saumur bij de heer Du Fos [<].

[ Vgl. Giambattista della Porta, Magia naturalis (Napels 1589), Natural Magick (Londen 1658): 20.IV: "like a Tortois crawling", als een kruipende schildpad.]

Tellurium
Derde aardbeweging uitgelegd met een instrument.

Toen Willebrord Snellius*) de trepidatie-beweging°) in de aarde ging verklaren hield hij in zijn linkerhand een houten bol voor de stilstaande zon, en in zijn rechterhand een andere bol, door langwerpig hout met de eerste verbonden, voor de beweeglijke aarde.
Hij liet deze om de zon draaien, zodanig dat de polen van de aarde steeds in dezelfde richting wezen, zoals bij de echte aarde, waarbij eenzelfde streek (hoe de beweging ook is) voortdurend gericht blijft naar de stilstaande polen van de achtste hemel. Dit kan misschien op deze manier gedaan zijn:

In de figuur was gd doorgetrokken voorbij d tot het 2e
snijpunt met cirkel def, ook d genoemd; daarna is dd
doorgestreept. [NB: de linker e zal f moeten zijn.]

De zon is abc, de beweeglijke aarde dfe, en gd en he zijn twee houtjes beweegbaar op de punten g, h, d, e. De lijn lm zal steeds evenwijdig met het papier blijven als dfe omhoog komt^#). Aangezien immers gd en he gelijk zijn, zal, als dfe boven abc geheven wordt, vlak dfe evenwijdig zijn met vlak abc, dus ook lm, enz. [>]

*) Willebrord Snellius (1580 - 1626), zoon van de Leidse wiskunde-hoogleraar Rudolph Snellius, doceerde vanaf 1600 de Almagest, en bezocht Tycho Brahe en Kepler in Praag. Vanaf 1605 publiceerde hij een Latijnse vertaling van het werk van Stevin. In 1613 volgde hij zijn vader op [>].
°) Meer over deze kwestie op p. 253. [Deze 'derde beweging' is geen beweging.]
[ Bedoeld wordt: de 'derde beweging' die Copernicus aannam voor het constant blijven van de aardas tijdens een jaarlijkse omloop (De revolutionibus, 1543, fol. 10v-11v).
Zie hiervoor de uitleg bij Stevin, en in W. J. Blaeu, Tweevoudigh onderwijs, 1634, p. 9: 'Van de drievoudige loop des Aerdkloots' (Lat., Fr.).
Meestal werd met de 'trepidatie' bedoeld een heen en weer gaan van het lentepunt, zie b.v, Thabit volgens Maurolyco, De sphaera liber unus, 1575, p. 24: "Tebitius ... prius commentus est trepidationis motum".]

[ ^#) En: g gaat van je af, h komt naar je toe.

Het mechaniek is hier te zien (groot) in een tellurium van A. J. Bokma, 1844 (Planetarium-boek Eisee Eisinga, 1928, p. 372).

Andere mogelijkheid: met katrollen, zoals uitgelegd in de beschrijving (uit 1617) van Adriaan Anthonisz' tellurium.

Beeckman kende later Blaeu's tellurium, waarbij drie raderen de aardas constant hielden.]

Kaarsvet

Gesmolten kaarsvet neemt meer ruimte in dan wanneer het koud is..
* Ik vraag me af waarom gesmolten kaarsvet meer ruimte inneemt dan wanneer het koud is, en water meer dan ijs*). Kan soms een substantie, die alle gedeelten van een plaats geheel omvat, verder samengedrukt worden, zodat ze met dezelfde hoeveelheid minder ruimte beslaat, of dan weer meer? Of wordt er veeleer vuursubstantie bijgemengd wanneer ze gesmolten wordt, en neemt het daarom meer ruimte in? En als die ontsnapt verandert water in ijs enz. [>]

*) [Later andersom.] De laatste woorden later onderstreept, misschien aanduiding bij verbetering.

[ 22 ]

Kopglas

Aantrekking van kopglaasjes.
Hoe komt het dat een koude doek, bij kopglaasjes*) gelegd, vrij sterk wordt aangetrokken?

[ *) Lat.: 'cucurbitula', pompoentje; zie ook 'koppen' en 'kopglas' bij WNT. De cucrbitula libellus, Par. 1541.]

[ Ned. ]

Warmte in kopglaasje en in een glas.
Fernel, Lib. 4, 3*) zegt dat, als in een gesloten kopglaasje aangestoken vuur is, en dan een spleet wordt geopend, er terstond met zeer grote kracht lucht zal binnendringen.

En ik heb een glas, voor de helft gevuld met water, afgesloten en dichtbij een zacht vuurtje gebracht; toen kwam er bij het openen van een spleet walm uit met grote kracht. Denk dus maar dat wat daar ontbrak, hier teveel was.

*) Jean F. Fernel [>], Universa Medicina (Parijs 1554, Frankfurt 1581).
[ Lugd. 1602 (in Cat. Med., fol. 1), zie daar p. 97, r. 40.
John M. Forrester (transl.), The Physiologia of Jean Fernel (1567), Phil. 2003, p. 265.]

[ 23 ]

Vacuüm

Vacuüm schijnt te bestaan.

De natuurfilosofen zeggen dat lichamen elkaar niet kunnen binnendringen en anderzijds dat één deel water, als het lucht wordt, spoedig een tienmaal grotere ruimte vult*). Waaruit schijnt te volgen dat de lucht bestaat uit zoveel materie als er water was, en overgebleven lege ruimte.

Vacuüm wordt bewezen door beweging.

Hetzelfde bewijzen ze uit de beweging van lichamen. Als immers lucht in een of ander deel bewogen is, zal, als de delen zonder tussenruimte verbonden zijn, tegelijk en ineens het uiterste van de lucht bewegen dat recht tegenover het bewogen deel is.
Want stel je je bolletjes voor die zonder iets ertussen tegen elkaar gelegd zijn, dan zul je zien dat als het eerste bewogen is ook het laatste tegelijkertijd beweegt, wat in lucht ongerijmd zou zijn. En je zult niet zeggen dat delen van lucht niet vast zijn, maar ijl, zodat ze samengeperst kunnen worden; maar, zeg ik, ze kunnen niet samengeperst worden als ertussen niet vacuüm is, waarin de zijden van de delen moeten gaan.

Vacuüm wegens luchtstromingen.

En ook, het is werkelijk ongerijmd dat er in lucht stroming komt zonder vacuüm, wat de rede zeker niet toelaat: lucht stroomt toch rechtstreeks weg van de stoot van een bewegend ding waarmee een vrij groot deel van de lucht weggeduwd wordt; maar er achter blijft hij ijler over. Want meteen weggehaald, keert hij niet snel terug, en hij trekt niet meteen andere aan, tenzij je zegt dat die ook meteen een derde aantrekt en dat hij zo meteen tot in het oneindige beweegt.

*) Vergelijk Aristoteles, de Gen. et Corrupt., Lib. II, cap. 6. [>]
[ Eind 1613 had Beeckman een briefwisseling over o.a. het vacuüm (met het voorbeeld van de rij bolletjes) met Jeremias van Laren, student in Franeker, zie T. 4, p. 26-31.
In 1633 deed Beeckman een proef om aan te tonen dat water niet verandert in lucht (>).]

Buskruit

Hoeveel verdunning.
* Buskruit dient als bewijs ervan, hoezeer dingen zich samentrekken en verspreiden. Als het is aangestoken zoekt het immers met zoveel drang een grotere plaatsruimte, dat het vaak grote gewichten over een enorme afstand voortstoot, en dat het zich in die toestand weinig lijkt te kunnen samentrekken. [>]

Terugkeer uit samentrekking naar de eerste toestand.
Zo kun je ook niet makkelijk lucht, hoewel die midden in zich niet weinig vacuüm bevat, merkbaar samenpersen tot een beperktere plaats. De delen ervan verhouden zich namelijk zo tot elkaar, dat ze niet in de lege ruimtes ertussen gaan, en dat bolheid en holheid niet in elkaar passen.

Poriën en scherpe kanten: sleutel en slot

Poriën passen bij scherpte kanten, en andersom.
* Wat moeten we dus van dit alles vinden? Natuurlijk — zoals een bouwmeester zich de eerste beginselen*) van een huis verschaft, een deur, een venster, deurposten, balken, dakbedekking, stenen; en zoals koning Salomo de eerste beginselen van de tempel zodaning heeft ontworpen, dat de delen zonder een hamerslag samengingen, en heel voortreffelijk bij elkaar pasten — dat God zo de natuurlijke eerste beginselen van de natuur heeft gemaakt, die zodanig met elkaar overeenkomen, met openingen die bij sleutels passen, dat daaruit bepaalde dingen ontstaan: stenen, bomen, dieren.
Zo laten de eerste beginselen van water vuur toe, hetzij binnenin, hetzij rondom, en als dit helemaal vervliegt wordt het daardoor ijs. Zo passen de beginselen van water bij meel, zodat voor een deel de aan alle kanten verschillende beginselen, of samengestelde, in het meel komen en dan zo met elkaar verenigd een consistentie geven, die ze apart niet zouden kunnen geven.

[ *) Lat. 'primordia'.]

[ 24 ]

Zo past water bij te besproeien aarde, kwikzilver bij metalen, hetzij omdat die eerste beginselen zelf zo poreus zijn, of als ze vast zijn, omdat daaruit samengestelde wegens zo'n vorm van de beginselen noodzakelijk zulke doorgangen bevatten, die alleen deze beginselen in zich opnemen, en niet andere, of zulke daaruit samengestelde wegens zo'n vorm daarvan.

* Het gebeurt ook soms dat zilver, gebroken door sterk water, een grote ruimte inneemt, omdat dit water het verdeelt in delen die niet bij elkaar passen; het zilver wordt immers op deze manier niet gebroken tot op de beginselen zelf. Daarom is het niet vreemd als de grootte verandert, al naar gelang de verschilende wijze van breken en van de delen.
Zo wordt buskruit gebroken in zeer kleine delen die niet passen; in veel gevallen ook verdwijnt de band terstond en keert die nooit terug. Zo wordt pottenbakkersaarde steen, hetzij omdat die door vuur wordt ontbonden in de juiste beginselen, of omdat de band die ze bindt van meer naar binnen gelegen deeltjes komt, en het vuur de poriën van de aarde opent. Gesmolten zilver trekt zich samen, omdat het in zulke deeltjes wordt ontbonden. Vloeibaar gemaakt glas is taaier omdat de punten van het vuur zo goed passen bij de poriën daarvan. IJzer wordt gehamerd omdat dit is tot smelten brengen, terwijl vuur de deeltjes ervan scheidt.

Vna willekeurige substabties zijn de eerste beginselen zo groot, dat ze de poriën van willekeurige substanties niet binnendringen. Uit zo stompe delen bestaan willekeurige substanties, zoals hout, dat door kwik niet gescheiden kan worden; of het is van zo zachte delen dat ze door de zwaarte ervan buigen, en zo wordt de doorgang verhinderd.

Ongeremde beweging

Eens bewogen voorwerpen komen nooit tot rust tenzij ze geremd worden.

Elk ding dat eenmaal bewogen is, komt nooit tot rust behalve door belemmering van buiten.*) En hoe zwakker de belemmering is, des te langduriger het bewogene beweegt.
Als immers iets omhoog geworpen wordt en tegelijk in het rond bewogen, zal het volgens de waarneming niet tot rust komen voordat het terug is op de grond; en als het eindelijk tot rust komt, gebeurt dat niet door een gelijkmatige belemmering, maar door een ongelijkmatige belemmering, omdat nu eens dit deel van de lucht en dan weer dat deel het bewegende ding raakt.

*) Eerste vermelding van het traagheidsbeginsel (vgl. draaiende hemel [<]).
[ Bij vrije val [>]; in een cirkel, Aarde om Zon [>]. Ned. [>]: "dat eens roert, roert altyt, soot niet belet en wort".]

Zon

Eens bewogen Zon komt nooit tot rust.

Je moet je een vacuüm voorstellen waarin alles sneller en langzamer beweegt naar gelang de grootte van de bewegende oorzaak. Zo beweegt de Zon, hoewel niet gesteld wordt dat hij aan de hemel vastzit, omdat hij toch niet dichterbij het middelpunt van zijn denkbeeldige cirkel kan komen, noch er verder vandaan kan zijn dan hij nu al is, als hij eenmaal bewogen is altijd volgens de snelheid van de bewegende oorzaak, zoals deze de Zon bewoog en wel in een cirkelbaan alsof hij aan de straal hing.

Steen

Een in vacuüm weggegooide steen komt niet tot rust.

Zo beweegt een steen, weggegooid in het vacuüm, voortdurend; doch lucht hindert hem, die hem steeds opnieuw tegemoet komt, en die zo maakt dat zijn beweging wordt verminderd. Wat echter de Filosofen zeggen, dat de kracht in de steen is gedrukt, lijkt zonder reden.

[ 25 ]

Wie kan immers vatten wat die kracht is, of hoe die de steen in beweging houdt, of in welk deel van de steen die zit? Maar het is heel gemakkelijk te vatten, dat een beweging in vacuüm nooit tot rust komt, omdat er geen oorzaak optreedt die de beweging verandert; niets wordt immers veranderd zonder een of andere oorzaak van de verandering. Als je er bijvoorbeeld een ding op legt en beide tegelijk in beweging brengt, en plotseling één van beide wegtrekt, zal het andere niettemin in de beweging volharden.

Opvangen

Hoe een steen zachter opgevangen kan worden.

* Als je een steen in de hoogte gooit en deze opvangt met een schaaltje in rust, zal hij een harde val maken. Als je echter, wanneer de vallende steen dichtbij het schaaltje is, het schaaltje op het laatste ogenblik omlaag beweegt, zal de val in het schaaltje zachter zijn, wat je kunt opmaken uit de klop. De oorzaak is dat door het omlaag bewegende schaaltje de lucht bij de plaats ervan terstond breekt en gaat wervelen, en wervelend de aankomende steen ontmoet, en op deze manier een hevige val verhindert.

Breken

Gehelen kunnen niet breken.

Wat geen poriën heeft lijkt niet te kunnen breken. Geen enkele scherpe punt zal er immers in doordringen tenzij delen wijken; doch de delen kunnen niet wijken, als de punt nog niet is binnengedrongen. Ook als iemand beweert dat het kan breken op andere manieren: wanneer delen niet verder samengetrokken kunnen worden, zullen ze alle tegelijk invloed ondervinden, zodat het noodzakelijk zou zijn dat het ineens zou barsten, wat absurd is.
Als echter iets zodanig tegen iets anders is geplaatst dat er geen vacuüm tussen is, lijkt het te kunnen worden gescheiden, omdat het niet zo is dat alle delen één geheel zijn zoals bij de eerste beginselen, waarvan alle delen, die daarin te bedenken zijn, één en hetzelfde zijn; welke eenheid een geschapen substantie is, niet samengevoegd, maar enkelvoudig.

Zwaar en licht

Beweging van zware dingen omlaag.

* Waarom bewegen zware dingen omlaag? Is het soms omdat het hogere in voortdurende beweging is, en bij de Aarde hetzelfde gebeurt als bij een steen die naar het midden van een waterkolk gaat? Of is er soms een ijle stroom omlaag van subtiele lichamen, vanaf de hoogste delen gelijkmatig rondom, die alles wat in de weg komt neerdrukt? En omdat deze stroom omlaag van subtiele delen is dringt deze door de meeste dingen heen, en drukt niet op de gehele substantie wegens de vrij grote poriën, en deze worden licht van gewicht genoemd.
De overige dingen, die compacter van aard zijn, worden zwaar genoemd omdat deze stroom omlaag er sterker tegenaan komt: wegens de compactheid immers vliegt er weinig van deze delen door, ook al zijn ze subtiel. [>]

Veer wordt niet ver gegooid.

Dat nu bij het omhoog gooien van een steen en een veer met dezelfde of even grote kracht, de steen hoger komt, heeft een andere reden. Hier is immers meer van belang de dichte lucht dan de genoemde stroom omlaag. Doordat dus de lucht niet doordringt, maar slechts het oppervlak treft, en aangezien van iets dat lichter is, d.w.z. minder dicht, het oppervlak groter is, volgt dat de lucht het lichtere meer in de weg zit en verhindert dat het blijft bewegen, zoals in vacuüm. Maar het dichtere wordt bij het vallen minder belemmerd door de lucht.

[ 26 ]

Geen vlucht voor vacuüm

Vlucht voor vacuüm wordt bestreden.

* Waarom stijgen zware dingen wegens afkeer van vacuüm? Kan vacuüm dan iets doen? Of zitten de dingen soms met een band aan elkaar vast? Maar waarom, als er één (hoe ook) beweegt, volgen dan niet de andere door de gemeenschappelijke band?

Laat het dus zo gezegd worden: die stroom omlaag (zie hierboven) is niet zacht en niet zwak, maar hevig en geweldig, zoals wanneer door ons op iets zachts gedrukt wordt: als daarin lege ruimte is, wordt deze meteen gevuld; zoals duidelijk wordt aan wie het probeert.

Maar, zul je zeggen, als die druk zo hevig is, waarom beïnvloedt hij ons lichaam dan niet? Ik antwoord: omdat die druk van alle kanten gelijkmatig is, en geen deel van zijn plaats bewogen wordt omdat ze alle evenzeer beïnvloed worden. Zo wordt ook op zwemmers en duikers een grote kracht van het water gezet, die ze anders buiten het water niet kunnen verdragen; maar omdat het water van alle kanten in gelijke mate op hen drukt, hebben ze geen pijn.
En dat het omringende met zo'n geweld drukt op een lege ruimte, gebeurt niet anders dan wanneer iemand op de bodem ligt van een vat vol met water, boven een opening in de bodem: want dan pas voelt hij de kracht van het water dat van boven op hem drukt.
Zie Stevin, boek 5, Van de Weeghconst.*) [>]

*) Wisconstighe Ghedachtnissen, 4e stuk (1605), 'Waterwichtdaet', p. 168.

[ Met nevenstaande figuur. Eerdere editie: 1586, p. 62-3.]

Aarde

Aarde in het midden van de wereld.

Waarom is de Aarde in het midden van het heelal? Ik antwoord weer: aangezien de hemel alles omvat.
Als sommige materie in de ruimte samenkomt met andere, is er meer vacuüm;, dus wat de Aarde is trekt die materie naar zich toe. En aangezien alle delen van de wereld zo trekken, is er geen dat overwint en laten ze de Aarde in het midden staan, en als er iets van het midden zou weggaan, dringt het naar het midden omdat dan in een deel er tegenover het vacuuüm oveerwint.
— Dit terloops, tenzij er een reden wordt gegeven waarom vacuüm kan trekken. [<,>]

Kwadratuur

Kwadratuur van de cirkel is natuurkundig mogelijk, wiskundig niet.
* Is de kwadratuur van de cirkel mogelijk?
Mijn antwoord is: Als je bedoelt natuurkundig, welzeker. Want niets natuurkundigs wordt tot in het oneindige verdeeld; de natuurkundige eerste beginselen zullen dan een gemeenschappelijke maat zijn van cirkel en vierkant, dus een gelijk aantal van deze maat-eenheden maken een cirkel en een vierkant.
Maar aangezien deze zelfde natuurkundige beginselen niet tot in het oneindige verdeeld kunnen worden, is er wiskundig gezien twijfel, hoewel een groter en een kleiner vierkant kan worden gegeven, of natuurkundig kan worden gedacht dat het gelijk is.
En geen wonder. Een rechte is immers onmeetbaar met een rechte, en een rechtlijnige figuur met een rechtlijnige figuur. Waarom zou dan niet gezegd kunnen worden dat een cirkelvormige lijn onmeetbaar is met een rechte, en een cirkel met een rechtlijnige figuur?
En wat meer zegt: de hoek tussen een raaklijn en de omtrek is volstrekt onmeetbaar met een hoek tussen rechte lijnen, al kan deze groter en kleiner dan de eerste worden gegeven.

[ 27 ]

Maantje

Kwadratuur van maantje heeft niets te maken met cirkel

* De kwadratuur van het maantje van Hippocrates*) is helemaal niet verbazend, en geen argument voor de kwadratuur van de cirkel. Het maantje is namelijk samengesteld uit een bolle en een holle lijn, en wel met een rationale verhouding°).
Alsof iemand de kwadratuur zou vinden van de rechtlijnige figuur, die er is bij een cirkel tussen het ingeschreven en het omgeschreven vierkant, waarvan het ene deel wordt omvat door de binnenkant van de cirkel en rechten, het andere door de buitenkant van de cirkel en rechten.

*) De 'maantjes van Hippocrates' worden genoemd door Clavius in Geometria practica [1604], 357 [figuur]. Later citeert Beeckman uit dit werk [1614].
[ °) Dit geldt niet voor de linkerfiguur hier onder, wel voor de rechter, maar de kwadratuur van deze drie maantjes was volgens Clavius nog niet gevonden.]

Clavius, maantjes van Hippocrates

Irrationaal

Irrationale verhouding van lijnen.
* Waarom zijn twee lijnen ten opzichte van elkaar irrationaal?
Mijn antwoord is: omdat een willekeurige lijn in gedachten tot in het oneindige verdeeld kan worden; en aangezien een verdeling die werkelijk met een gedachte plaatsvindt, eindig is, blijft een oneindig iets over; er is immers iets eindigs afgetrokken van iets oneindigs. Wanneer dus een kleinste maat of een kleinste lijn, die metterdaad gevonden is, in oneindig veel kleinere is te delen, volgt dat deze kleinere oneindig veel van elkaar verschillen en dat van alle lijnen, die na elke werkelijke gedachte nog een verdeling overlaten, het onderlinge verschil oneindig groot is.

Deling tot in het oneindige.
Doch hoe een lijn in gedachten tot in het oneindige deelbaar kan zijn, misschien zal iemand er profijt van hebben het zich op deze manier voor te stellen.
Dat een lijn en delen van een lijn tot in het oneindige vergroot kunnen worden, stellen we ons voor als we denken dat vanaf één punt twee lijnen, die een hoek maken, tot in het oneindige lopen. Waarmee we ons voorstellen dat de basis en delen van de basis tot in het oneindige uitgroeien en oneindig ver van dat punt of middelpunt verwijderd zijn.
Als dan de genoemde basis, oneindig ver van het punt van samenkomst, eindig wordt gesteld, kunnen we ons zonder moeite oneindig veel lijnen voorstellen, kleiner dan de basis, die we nooit werkelijk in gedachten kunnen verdelen.
Want stel dat die kleinere lijnen van het genoemde punt een voet verwijderd zijn, twee voeten, en zo voorts, tot zo ver als het werkelijk in gedachten kan. Aangezien nu gedachten in werkelijkheid eindig zijn, en gesteld is dat de genoemde basis oneindig ver weg staat, is elke afstand tot het genoemde punt die in een werkelijke gedachte wordt vastgesteld, oneindig ver van de basis; als iets eindigs wordt afgetrokken van iets oneindigs, is het resultaat immers oneindig.

Oneindig

Iets eindigs beweegt niet door iets oneindigs van dezelfde soort.
* Gevraagd wordt: hoe kan iets in een enkel uur, wat een eindige tijd is, bewegen over een lijn, terwijl die in oneindig veel delen deelbaar is?

Ik antwoord: Tijd is niet eindiger dan een lijn, en een enkel uur is even goed in oneindig veel delen te delen*) als een lijn. Of, als je een uur eindig stelt, moet ook een lijn van een el eindig gesteld worden.
Het is dus geen wonder als iets eindigs in een eindige tijd over iets eindigs beweegt; of iets dat in gedachten oneindig deelbaar is, in een tijd die in gedachten oneindig deelbaar is, over iets dat in gedachten oneindig deelbaar is.
Zo wordt door de beweging van een bol een lijn beschreven, en dit is niet: door iets ondeelbaars in de bol, iets deelbaars beschreven; maar: door iets deelbaars in de bol, iets deelbaars, en door iets ondeelbaars in de bol, als er iets van is in de bol, iets ondeelbaars, als er iets van is in de lijn.

[ *) Dit was al bedacht door Zeno: Achilles en de schildpad — een wiskundige uitleg is hier niet nodig, de redenering is alleen: tijdens het inhalen wordt niet ingehaald.]

[ 28 ]

Oneindig bij verdeling en oneindig bij samenstelling.

Dus iets dat slechts oneindig is bij verdeling, zoals een bol, zal nooit verder komen dan iets dat oneindig is bij samenstelling — nooit verder komen, wil zeggen: verder komen in een oneindige tijd.
Een punt echter, of iets dat slechts oneindig is bij verdeling, zoals een bol, zal tenslotte verder komen dan iets anders dat slechts oneindig is bij verdeling, zoals een enkele mijl — tenslotte verder komen, wil zeggen: verder komen in een tijd, die slechts oneindig is bij verdeling, zoals in een enkel uur, namelijk iets eindigs over iets eindigs in een eindige tijd.

Geest

Wijsvinger en middelvinger over elkaar gelegd, doen menen dat één bol twee zijn.
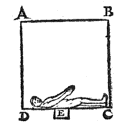
* Te onderzoeken de reden waarom, als wijsvinger en middelvinger over elkaar zijn gelegd en als ze een enkel bolletje aanraken, er twee lijken te worden aangeraakt [>]. En welk deel van de wijsvinger de bol gewoonlijk niet aanneemt van dat deel van de middelvinger, en welk deel van de middelvinger de bol gewoonlijk niet opneemt van dat deel van de wijsvinger. Waarom het voor de ene lijkt alsof hij een andere bol aanneemt dan die welke in de andere vinger was.
Is er soms een of andere continuïteit in de geesten*) van de mens, die wil dat het verband zo is en niet anders? En lijkt een aanraking enkelvoudig als die volgens die continuïteit van de geest beweegt, en samengesteld of meervoudig als dit niet zo is?

Hierbij: of dat niet die geest is die, als zaad in de baarmoeder is samengegaan, van nature op een bijzondere manier aan de afzonderlijke delen de eigen plaatsen toebedeelt? Omdat de geest van elk deel met zijn eigen deel bekleed is en de geesten zich zo en niet anders met elkaar verbinden.

Tenslotte: wat bij een magneet [>] de reden is, waarom afzonderlijke gescheiden delen niet in een willekeurige opstelling bij elkaar komen, maar met inachtneming van de hemelstreken, waarnaar ze vanaf het begin van nature beschikt zijn geweest.

[ *) Lat.: 'spiritibus', vluchtige stoffen. Vergelijk p. 17 hierboven: 'wijngeest' en 'mijn geesten'. Op p. 103v: "zenuwen, daar ze vol met geest zijn".
Enkele andere notities waarin 'spiritus' voorkomt:
1614: "Nu gaat er van een magneet een soort geest uit" (p. 36v).
1617: "... de hele structuur van ons lichaam lijdt. Want er zijn levensgeesten verspreid over de hele microkosmos ... dat in de hersenen gerijpte geesten een dergelijke aard krijgen als zenuwen, die ook door materie van de hersenen gemaakt worden" (p. 124v).
1617: "En het is niet wonderlijker dat er een geest-achtige substantie zit in de omhulsels (van slagaders), dan in zichtbare zenuwen, die zeker geen holtes hebben" (p. 157v).
1618: "Als dus de daling van de steen gaat met onderscheiden intervallen, terwijl de Aarde trekt met lichamelijke geesten ..." (p. 263v).
1619: "... al de spiritus en crachten des geests ... al dat eenichsins in de hersenen verborgen licht, dat openbaert sich dan door de deucht der geconjungeerde geesten." (p. 271).
1621: "Geest van de hersenen, hoe die zulke zware botten beweegt" (T. 2, p. 174v).
1626: "de spiritus van den seylsteen, dewelcke gestadich daeruyt vlieght ... Desen geest vliecht also gelyck se uyt den seylsteen kompt, ende gaet oock so sitten int yser" (T. 2, p. 339).
1628: "seght hy (Francis Bacon) ... dat de dieren ende planten spiritus of geest hebben in gootkens ... aeren of gootkens" (T. 3, p. 64).
1628: "omdat het [water] de corste van het yser socht maeckt ende also de sprirtus of geesten eenen wech maeckt om uyt te kommen." (T. 3, p. 56).
1634: "Als men licht ... omdat de borst opgelicht moet worden met macht van geest" (T. 3, p. 357).
In Johan van Beverwijck, Schat der ongesontheyt (Dordr. 1642) zijn ook veel 'geesten' te vinden.
Joh. de Gorter, De gezuiverde heelkonst (Leiden 1735), p. 187: "Spiritus. Dat door deze Fibrillae een vocht vloeit zal blyken, als men overweegt ...", p. 189: "in eene groote quantiteit ... Deze vocht moet ook zeer dun wezen ... dat men dezelve niet kan ontdekken"; Blad-wyzer: "Spiritus, geest".
Veel vragen over geesten in:
Idem, vert. H. Korp, Nieuwe gezuiverde Heelkonst (Leien 1746), vanaf §. 766, zie Blad-wyzer, o.a. (§. 793) "of de geesten een soort van ligt-stof zijn" en (§. 1183 e.v.) "Worden de bewogene geesten in het voelende zintuig naar de algemeene gewaarwordings-plaats gevoerd, op dat zy het denkbeeld van gevoel verschaffen?"]

Licht

Licht, door iets weerkaatst, is materie van zien, zelfs ook van kleuren.
* Bij alle dingen is het zeker dat er door hun beweging (en ze bewegen klaarblijkelijk of*) door straling van sterren), onophoudelijk iets vanaf stroomt. Wat is er immers dat de tand des tijds°) niet kan veranderen?

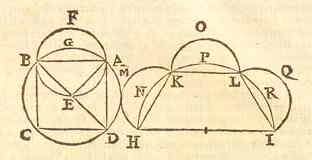
Maar misschien zal iemand zich afvragen of ook afdrukken^#) van dingen lichamelijke stromen zijn uit die dingen. Als dit bevestigd wordt, waarom zien we dan niet bij nacht? Zijn de afdrukken soms wel lichamen, maar niet van hetgene dat gezien wordt? maar licht zelf dat voortkomt uit het lichaam van de lichtbronnen en dat, gebroken aan de objecten die we zien, in onze ogen valt? En een verschillende manier van inval, een verschil van weerkaatsing aan poriën van het object, doet bij een overvloed aan licht verschillende kleuren ontstaan, en verschillende manieren van zien en van de afdrukken. [>]

[ *) Ed. 1644: "manifeste aut", ook in noot ed. de Waard.]
°) Vergilius Aen., Lib. III, vs. 415 [Lat.: "edax vetustas", ook Ovid. Metam., XV, 872].
[ ^#) Lat.: 'species', daarna 'species visibiles'. Zie het door Beeckman op p. 6 geciteerde werk:
Petrus Ramus, Opticae libri quatuor (1606), p. 3: "Manare autem atque fluere ex omni corpore sensili species", dat uit elk lichaam waarneembare 'species' ontstaan en wegvloeien; p. 4: Lucretius (ook vaak elders); p. 128: "materiae omnis expers", los van alle materie.
Benedino Gemelli, 'Isaac Beeckman as a reader of Francis Bacon's Sylva Sylvarum', in Journal of Early Modern Studies, 2-1 (2013), p. 69.
Fr. Bacon, Sylva Sylvarum or a Natural History, Londen 1627, p. 27:

The Species of Visibles seeme to be Emissions of Beames from the Object seene; Almost like Odours; save that they are more Incorporeall.

Beeckman, 1628: "... indien ghy meent, dat den blixem snelder vlieght dan het gesichte, id est species visibiles quas vocant" (T. III, p. 54).
E. J. Dijksterhuis, De mechanisering van het wereldbeeld (1950), p. 164:

Het begrip species is afkomstig uit een door Aristoteles aangegeven en door Thomas [van Aquino] uitgewerkte theorie over de wijze, waarop wij door zintuiglijke waarneming kennis van een ding verwerven. Wanneer wij bij voorbeeld een ding zien, is dit voorwerp, hoewel het zijn eigen en volledig bestaan buiten ons heeft, in zekeren zin ook in het gezichtsorgaan aanwezig, welke zijnswijze een species sensibilis genoemd wordt; de materialiteit van het voorwerp is daarbij afgelegd, maar de wezenskern is behouden gebleven; wordt nu deze species sensibilis onderworpen aan de werking van het intellectus agens (dat immers volgens de Thomistische opvatting een actieve kracht van het denkvermogen is) dan ontstaat de z. g. species intelligibilis, waarvan de aanwezigheid de bewuste waarneming van het ding buiten ons beduidt. In deze species intelligibilis is het ding in zekeren zin in ons en zijn wij het ding; zij is de zijnswijze van het gekende ding in den kennende.

Johannes Kepler verklaarde de beweging van de planeten om de Zon met een 'speciei motricis defluxus', een uitstroming van in beweging brengende 'species', zie T. 3, p. 99.
Christiaan Huygens noemt 'speciën' in notities bij 'Het leven van Descartes' (T. 10, p. 403).
Over Epicurus (Stanford Encycl. of Phil.):

All secondary properties, such as color and taste, will be explained as epiphenomena of atomic combinations, and perception of things at a distance by the continual emission of infinitesimally thin laminas from objects, which maintain the relevant features of the source (in the case of vision, for example, the laminas will preserve the atomic patterns specific to the color and shape of the object) and directly stimulate the relevant sense organ. This is a tricky thesis, and again posed puzzles: how do the lamina or simulacra, as Lucretius called them, of a mountain enter the eye, for example? In fragments? By somehow shrinking? We do not know the answer to this one.

Lucretius, De rerum natura IV, 42- in de vertaling van A. Rutgers van der Loeff:

Ik zeg dus, dat de dingen van hun oppervlak
afdrukken uit te zenden plegen, ijle vormen.
...
dat schijngestalten van de dingen ook bestaan,
die men beschouwen moet als 'n vlies of als een schil,
...
zoals wanneer bij zomertij
cicaden hun omkleedsel van zich schuiven en
zich pasgeboren kalfjes van hun vlies ontdoen
of aan de doornen slangenhuid wordt afgestroopt —
wij zien toch dikwijls fladdren in de struiken nog
het oude hulsel dat voor nieuw verwisseld werd —:
daar dit geschiedt, moet ook een ijle beeltenis
van 't oppervlak der dingen worden afgelicht.

Beeckman noemt Lucretius voor het eerst in 1614: T. I, p. 36.
Beeckmans promotie (1618), 3e stelling: "Quas vocant optici species visibiles sunt corpora.", Wat de optici 'species visibiles' noemen zijn lichamen.]

Geluid

Lucht is materie van geluid.

* Zo zal iemand zich afvragen of er geluidsmaterie voortkomt uit het klinkende ding of uit het gehoorde. Als dit zo is, waarom geeft dan een gespannen en weer losgelaten snaar niet eenzelfde of gelijkblijvende klank?
Is dan, zoals licht de algemene basis van het zien is, zo ook lucht de algemene basis van het gehoor en geschikte geluidsmaterie die, als ze de instrumenten van een levend wezen raakt, geluid genoemd wordt?
De diversiteit ervan berust op verschillend bewogen lucht, en lucht die in het gehoororgaan op verschillende wijze het bewustzijn beïnvloedt, niet zonder stoffelijk contact, direct of tenminste indirect. [>]

[ 29 ] [ juli 1613 - april 1614 ]

[ Ned. ]

Pilaren

Optisch tekenen van pilaren.

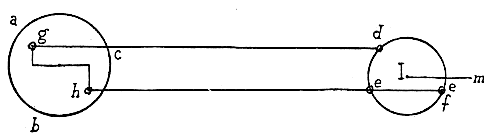
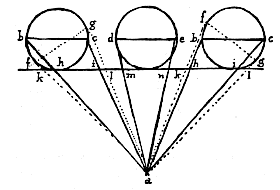Laat de cirkels hierbij pilaren zijn en de rechte fg [horizontaal] een glas waarop de genoemde pilaren optisch getekend moeten worden.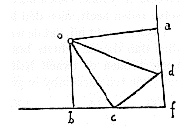
Als dan de dikte ervan wordt genomen door de middelpunten evenwijdig met het glas, zoals bc, de, bc, worden ze op het glas wel gelijk getekend, maar dit zal niet een tekening zijn van wat het oog ziet vanuit a. Verschillend dus, hetzij van kleuren hetzij van vorm, lijkt een pilaar op deze manier niet juist getekend te worden: het schilderij zal een toeschouwer immers anders toeschijnen dan de zaak zelf.
Als echter getekend wordt wat te zien is als fg, de, fg, zal de grootte daarvan op het glas fg ongelijk geschilderd moeten worden, en misschien niet weinig misvormd, wegens de geschilderde ongelijkheid van kl, mn, kl. [>]

[ 30 ]

Spiegels

Twee evenwijdige spiegels geven meer beelden.
lijnen

* Waarom verschijnen er met twee spiegels die met elkaar verbonden zijn, zoals ad en bc, meer beelden? Werpt een beeld soms ook een beeld van zichzelf? Niets is minder waar. Wat dan?

Het oog wordt teruggekaatst naar zichzelf uit a en b en zendt een beeld naar d, vanwaar het wordt teruggekaatst in c en vandaar keert het terug naar zichzelf, dat wil zeggen naar het oog o. En de hoeken ado, fdc, dcf en bco zijn zeker gelijk. Waarom zou deze terugkaatsing dan niet volbracht worden? [>]

[ De tekening klopt niet echt, het principe wel.

Punt c moet naar rechts, en punt d naar beneden, zodat er bij f een gelijkbenig driehoekje komt.

Het is te vinden door het spiegelbeeld van o achter a te spiegelen in de (verlengde) onderste spiegel; en dat van o onder b in de (verlengde) rechterspiegel.

NB: In dit stukje gebruikt Beeckman het woord 'imago' voor 'beeld'; op p. 29 hierboven ging het over 'species visibiles'.]

Weger

Redenering bij een weger.
In de mechanica zou gevraagd kunnen worden waarom een gewicht, op het langste deel van een weger gezet, meer zou wegen dan op gelijke afstand.

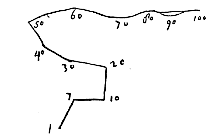
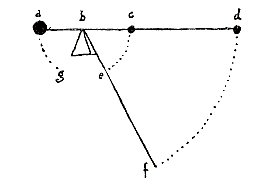ongelijkarmige balans Ik antwoord: Gegeven de weger abcd met het steunpunt bij b, een zwaarder gewicht a en een lichter gewicht c en d.
Het lichtere gewicht zal, geplaatst bij d, overwicht hebben op het gewicht bij a, maar bij c geplaatst zal het geen overwicht hebben.
Is er dan niets zo zwaar, zo sterk, dat het niet door een willekeurige kracht naar boven gebracht kan worden, als deze maar zo langzaam wordt toegepast, dat hij het wint op afzonderlijke stukjes?
Laat a twee ons zijn, en c één ons, en laat ab gelijk zijn aan cb. Dan zullen ook ag en ce gelijk zijn. Dan zijn evenveel gelijke stukjes te doorlopen voor één ons, als voor twee ons; de twee ons zal dan overwicht hebben.
Omdat voor de ene ons bij d driemaal zoveel stukjes zijn te doorlopen, voordat dit tot de plaats van rust komt, volgt dat het drukken bij d groter is en dat er bij a veel meer kracht vereist wordt om een stukje te doorlopen dan bij d.

Na deze notitie volgen vijf stukken over het weer:

1. Tempestatum collectio, ontleend aan Fernel
2. Journael anni 1613 en 1614 te Siricksee, 29 juli 1613 - 3 april 1614 [<]
3. Observata Scouteni in Gallia a Montauban, 23 mei - 24 sept. 1613
4. Tempestatum collectio, ontleend aan Quercetanus
5. Journael anni 1614 Siericksee, 15 okt. - 31 dec. 1614. [>]

Home | Isack Beeckman | 1613 v (top) | vervolg