Meridiaan
Meridiaan vinden.
* Het vinden van de meridiaan is algemeen bekend, namelijk dat die komt tussen twee punten op de horizon, waarvan het ene voor het middaguur, het andere erna, dezelfde zonshoogte aangeeft. Maar met het ene venster op het oosten en het andere op het westen, heb ik die verkregen met een magnetische naald, op de volgende manier;
In het ene venster heb ik voor het middaguur een hoogte opgetekend, in het andere na het middaguur dezelfde hoogte en daarvan heb ik de punten opgetekend op gelijke cirkels. Daarna heb ik uit het middelpunt van de cirkels lijnen getrokken volgens de magnetische naald, hetzij gewoon, zonder voorbereiding naar een bepaalde plaats, of ook met voorbereiding naar een of andere plaats.
Deze in de beide vensters getrokken lijnen zijn noodzakelijk evenwijdig, omdat de naald op dezelfde plaats altijd in dezelfde richting gaat staan. Ik heb dus van het ene punt, neem dat voor het middaguur, de afstand genomen tot die magnetische lijn en die aangebracht in het andere venster op de andere cirkel bij de andere magnetische lijn naar het westen. En zo kreeg ik op eenzelfde cirkel punten van voor het middaguur en erna met dezelfde zonshoogte, in het midden waarvan de ware meridiaan is.
Vitriool
Spiritus vitrioli.
De vluchtige stof van vitriool, de bedwinger van die beruchte epilepsie enz., wordt verkregen als vitriool met kwik wordt gedestilleerd en het destillaat in water opgelost, het kwik wordt verwijderd, en het water verdampt. Overblijft een vluchtige stof, die andere vluchtige stoffen doet stollen en die lichamen oplost. — Quercetanus*).
Dit is dat olijfkleurige gedestilleerde water, gemengd met de vluchtige stof van tartarus#), dat door toevoeging van wit gesublimeerd antimoon zonder smaak wordt, getempereerd met een grote hoeveelheid water. — Mr Du Foes°).
*) In de werken van Quercetanus [Joseph Duchesne] is de passage niet exact teruggevonden.
[ Liber de priscorum philosophorum verae medicinae materia (1603), p. 106: "domator epilepsiae".]
[ #) 'Gheest van Wyn-Steen' (wijnsteengeest) in Medicina pharmaceutica (1681), p. 979.
Over wijnsteen (tartarus) een wijsteengeest ook: Catechismus der apothecars-kunst (1813), p. 176 en 181; Handleiding tot de kennis der scheikundige geneesmiddelen en vergiften, 1 (1841), p. 384.]
°) Misschien David du Fos [>], in 1618 gedeputeerde bij de protestantse synode te Orthez.
Telescoop
Principe van de telescoop.
* Het instrument waarmee vanuit de verte kleine dingen worden gezien en dat in het Frans lunette wordt genoemd, is naar ik heb bevonden samengesteld uit een brandglas, dat wil zeggen de gezichtshoeken vergrotend, en een glas dat de gezichtshoeken verkleint.*)
*) Heeft Beeckman de verrekijker in Saumur leren kennen? Of in Middelburg? Of in Leiden?
"Ik was dus in Leiden in 1609" schreef Deschamps, geneesheer te Bergerac, op 5 mei 1642 aan Mersenne, "waar Rudolphus Snellius, professor in de wiskunde (die ons les gaf uit de Optica van Ramus) na afloop van zijn les mij de gewone kijker toonde die slechts één buis had ...". [>]
|

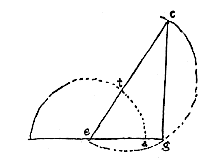
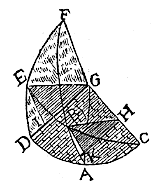 Omdat AB loodrecht op AC is, en straal AG loodrecht op deze, zal BK (opgericht op vlak DGC) op straal AG vallen. En omdat BH loodrecht is op straal GC, en HK loodrecht op deze, zal BK op dezelfde lijn HK vallen, dus op het snijpunt van HK en GA, volgens
Omdat AB loodrecht op AC is, en straal AG loodrecht op deze, zal BK (opgericht op vlak DGC) op straal AG vallen. En omdat BH loodrecht is op straal GC, en HK loodrecht op deze, zal BK op dezelfde lijn HK vallen, dus op het snijpunt van HK en GA, volgens 
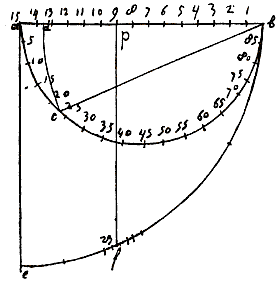 ab geeft het aantal mijlen aan van één graad op de evenaar of grootste cirkel.
ab geeft het aantal mijlen aan van één graad op de evenaar of grootste cirkel. 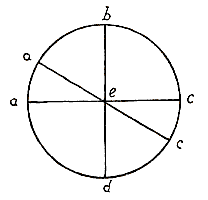 Daar dus bec niet lichter of zwaarder is dan aed, gaat a met evenveel kracht en snelheid omhoog als c omlaag gaat, ook hier op Aarde, daar a met de arm ae in elk opzicht dezelfde kracht heeft om te vallen als c.
Daar dus bec niet lichter of zwaarder is dan aed, gaat a met evenveel kracht en snelheid omhoog als c omlaag gaat, ook hier op Aarde, daar a met de arm ae in elk opzicht dezelfde kracht heeft om te vallen als c. 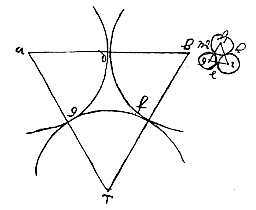 Want driehoek abc is gelijkvormig met de driehoek van de kleine cirkels, dus zoals het kwadraat van de diameters.
Want driehoek abc is gelijkvormig met de driehoek van de kleine cirkels, dus zoals het kwadraat van de diameters. 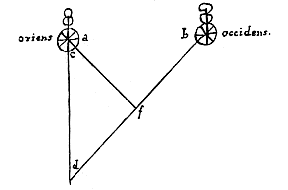 Want als d het begin is van de wind, en a en b zijn veraf gelegen steden, is het noodzakelijk dat er in a een andere wind waait dan in b.. Als dus is waargenomen dat op dezelfde tijd in a de wind uit het nooden*) kwam, en in b uit het noordoosten, is het zeker dat het eerste begin van de wind geweest is op het snijpunt van de lijnen dc en db.
Want als d het begin is van de wind, en a en b zijn veraf gelegen steden, is het noodzakelijk dat er in a een andere wind waait dan in b.. Als dus is waargenomen dat op dezelfde tijd in a de wind uit het nooden*) kwam, en in b uit het noordoosten, is het zeker dat het eerste begin van de wind geweest is op het snijpunt van de lijnen dc en db.