Schieten , hete lucht , kaars , weer , vering , zwaarte , luchtdruk , gewicht , zien , Basson
SchietenWaarom kogels uit langere buizen verder worden geschoten.Uit langere buizen worden bollen verder geschoten dan uit kortere, en dit zowel door blazen als met kruit*). Want met de mond tegen de opening van een houten buis blazen we uit, en de lucht die in de buis is stuwen we voort; en is er een bolletje, in de mond gehouden, of bij de mond in de buis liggend, en dit wordt getroffen door geblaas van de mond. Aangezien dus alle lucht in de buis door het blazen wordt voortgestuwd, wordt onvermijdelijk ook het bolletje, hoewel zwaarder dan lucht, voortbewogen, daar geen lucht het tegenhoudt. Nu hebben we eerder gehoord [<] dat in vacuüm voorwerpen door het kleinste duwtje gaan bewegen; hier evenwel is meer dan vacuum met betrekking tot de bol. Want lucht en geblaas stoten hem van achter; hij zal dus snel of langzaam bewegen naar de hevigheid van het geblaas dat uit de mond komt. Maar waarom beweegt hij niet even snel in kortere buizen, terwijl eerder gezegd is dat de vaart in het begin de snelste is van de hele vlucht? [<] Verder wordt in een korte buis de beginvaart en het geblaas van de mond niet minder krachtig gegeven dan in een langere buis. En het lijkt er niet toe te doen, dat de bol langer in die snelste beweging gehouden wordt in de langere buis dan in de kortere, want er kan slechts dit gewonnen worden dat de bol evenveel verder wordt geschoten als de buis langer is; dat wil zeggen, als deze drie voet langer is, dat hij drie voet verder geschoten wordt, omdat de bol zich buiten het eind van de langere buis niet sneller beweegt dan aan het eind van de kortere buis. Maar toch is dit niet waar. Daar immers lucht en geblaas wegens de lichtheid, en omdat ze oorzaak zijn van de bolbeweging, sneller bewegen dan de bol, is het zo dat het blazen voortdurend, zolang hij in de buis is, nog iets toevoegt aan de beweging van de eerste vaart. Want de bol wordt al buiten de buis waargenomen, ook bij de langste buizen, voordat het blazen van de mond ophoudt; maar als hij buiten de buis is verliest het geblaas, verstrooid over de wijde lucht en er overal door belemmerd, terstond alle kracht; in de buis echter, door geen omgevingslucht belemmerd, behoudt het die tot het uiteinde, en is het geblaas, bewegend in de buis, sneller dan de bol; maar buiten de buis is de bolbeweging sneller dan het blazen.
Als nu een buis zo lang zou zijn dat het blazen bij het uiteinde niet meer sneller zou bewegen dan de bol, dan zou uit zo'n buis de bol even ver geschoten worden als uit een kortere buis, met het blazen aangepast aan de beweging. Den 6en jan. 1623 te Rotterdam. *) Dit verschijnsel was besproken door Tartaglia, Quesiti et inventioni diverse (Venetië 1546 (fol. 18v-20v) [1554, 'Quesito undecimo', txt], Cardanus, de Subtilitate (Neurenberg 1550), ed. Lyon 1580 p. 93, en Benedetti, Div. specul. Lib. (Turijn 1585) p. 258. [ De laatste leert Beeckman pas later kennen: T. 3, p. 273, en dan schrijft hij (p. 275):]
Hete lucht niet door glasOok de heetste lucht gaat niet door glasDen 22en Jan. 1623 te Rotterdam.
Water wordt opgetrokken in een glas waarin een kaars brandt [<], niet omdat verdunde lucht tegelijk met vuur door poriën van het glas gaat [<]. Die lijkt er immers niet door te gaan, en bij geen enkele proef gebeurt dit, bij mijn weten; ja als het zou gebeuren, zou dat instrument waarmee ik de koude- en warmtegraad in de loop van de tijd aanteken [<], tenslotte tekortschieten, als warmte binnen zou dringen en altijd enige lucht met zich mee zou brengen. |
|
Er is ongetwijfeld enig verschil tussen de warmte van genoemd instrument en van een vlam brandend in een glas; daar is die immers overal gelijk, hier evenwel is het binnen heet, buiten koud. Maar niettemin, daar ik nooit bevonden heb dat lucht erdoor gaat, wil ik liever zeggen dat het water stijgt doordat de lucht, verdund voordat hij het water zou raken bij de opening, na het doven van de kaars verdicht wordt. Want zelf heb ik een beker omgekeerd en met de open kant in water gedaan, en aan de bovenkant heel warm gemaakt met vurige kolen; en toch is er geen water de beker ingekomen, maar veeleer ging er lucht uit, door bellen te maken, terwijl toch de lucht binnen hevig opgewarmd was. Kaars onder glas in waterKaars in omgekeerd glas in water, waarom hij dooft.De kaars nu gaat uit omdat de lucht, die de vlam omringt, niet door erop liggende lucht in de vlam wordt gedrongen, daar er geen lucht is die op deze lucht drukt; de glaskanten zitten immers in de weg. De lucht is dus in het glas in rust, ook als die in de vlam zelf verbruikt is, want als die verbruikt is, of liever verdund, verbreidt hij zich in het glas naar alle kanten. Maar deze plek heeft niet een kracht om andere lucht aan te trekken, zoals we hiervoor vaker hebben gezegd [<], behalve zoveel als er door luchtbeweging toevallig ter plaatse van de vlam komt, die ook zelf door de vlam verdund wordt, en kariger voorhanden is; zo komt het dat de vlam kleiner wordt. Want als de vrije buitenlucht naar de lege plaats wordt geduwd, sluit hij eerst de vlam van alle kanten in, perst hem samen en belet dat die zich te snel verspreidt; waardoor komt dat de vlam warmer is en de walm en olie sterker verdunt. Ten tweede beweegt hij bij het aankomen de vlam, zodat deze heftiger in de olie en walm gedrongen wordt. Ten derde doet hij ook zelf, daar hij door warmte verdund kan worden en met walm vermengd wordt, de walm uiteenspatten en scheiden, en de beweging toenemen. Dit alles mist een opgesloten vlam, in het begin enigszins, later zelfs geheel. Het weer voorspellenWeer voorspellen met glazen waarmee de warmte wordt bepaald.Wie de gesteldheden van de lucht van tevoren wil weten, moet veel van die glazen die lucht bij koude verdichten (zoals we eerder beschreven hebben [<,>]) opstellen op veel plaatsen, eerst even ver van de pool, om na te gaan wat de invloed is van de Maan en de overige planeten, in samenstand met allerlei vaste sterren. Daar de Maan immers elk uur bij andere vaste sterren staat, zullen er geen twee plaatsen op dezelfde breedtecirkel zijn, waar dezelfde hemelwerking kan komen. Want ook al ziet men Westelijker op een volgend uur precies diezelfde sterren, men ziet ze toch niet met zo'n positie van de Maan; wat wellicht veel uitmaakt, daar het vaak zo is dat de Maan een bepaalde stand heeft ten opzichte van de Zon, of een vast teken van de Dierenriem enz., die hij eerder niet had. En als het weinig blijkt uit te maken voor de verandering, zal het glas dit aangeven; of anders zullen we deze toeschrijven aan de natuurlijke gesteldheid van land en water ter plaatse. Daarna stel je glazen op meer naar het zuiden enz. [>] |
Westenwind door sterren?Of Westenwind komt door sterren ten Westen van de Zon.Maginus, Supplem. Isagog. Ephem., cap. XII,*) zegt dat Westenwinden ontstaan door sterren die Westelijk van de Zon zijn.
Maar ik kan niet begrijpen dat vaste sterren, hoe ze ook Westelijker zijn dan de Zon, niet op dezelfde manier inwerken op de volgende lucht, daar ze tegelijk met de Zon bewegen van Oost naar West. Waarschijnlijker kan dus lijken dat planeten, naar de Westelijke Zon toegaand en er vandaan gaand met de Zon in het Oosten, winden doen bewegen [<]. *) Ioannis Antoni Magini Patavini Ephemeridum caelestium motuum continuatio. Ab A.D. 1608 usque ad A. 1630, juxta Copernici observationes ... (Frankfurt 1610). Suppl. Cap. 12: 'Astrologicae ventorum prognosticationes'. °) Vergelijk p. 212, noot. Maan en magneetOp welke manire de Maan de wateren beweegt.Misschien is ook de kracht van de Maan, waarmee ze de Oceaan in beweging brengt, gelegen in verdunning van de lucht, natuurlijk door wegens de nabijheid de lucht te verdunnen boven de klaarblijkelijk zo uitgestrekte ruimte van de Oceaan, die dan op deze wijze minder op het water drukt, en het water naar het oosten doet bewegen, zodat dit daardoor wordt opgeheven, op plaatsen heel ver van het lichaam van de Maan, of van de tegenoverliggende stand ervan, anders dan de gewone mening. Zo heb ik ook gezegd [<] dat de 'spiritus'*) van een magneet de ruimte tussen het ijzer en de magneet bezet, en dat zo beide dan naar elkaar toe worden gedrukt door de leunende lucht, daar deze 'spiritus' zodanig overeenkomt met de poriën van het ijzer dat hij er zonder moeite doorheen gaat, maar dat de 'spiritus' van de magneet die van de andere kant wegvloeit, niet in ijzer doordringt en het van zich verwijdert. Of als het absurd lijkt dat de Maan door warmte bewerkt wat de Zon met zoveel warmte niet doet, zeg dan dat 'spiritus' van de Maan, door warmte van de Zon naar buiten gebracht, die wateren binnengaat en ze, als het ware door gisting, meer gezwollen maakt en zo een beweging opwekt, en die algemeen verbreidt. En die zwelling of beweging, in een kleine ruimte heel klein en onmerkbaar, wordt groot en merkbaar als de hele Oceaan, naar een bepaalde plaats bewegend, daar tot stilstand komt, en voortdurend volgende wateren ontvangt, zoals eerder ergens nauwkeuriger [<]. [>]
Strabo, bibl. 15: "in Libië zoals ook in Ethiopië regent het veel in de zomer; in de winter is er droogte".°) [ *) Zie ook T. 1, p. 101 en hierna, p. 339:
°) Deze passage wordt niet teruggevonden in de Geôgraphikôn biblia iz' (de Situ orbis, Lib. XVII) [1549, Engl.]. [ Gevonden in 'Chrestomathiae ex Strabonis Geographicis', ed. Almeloveen 1707, p. 1317; en — via Hager, Geographischer Büchersaal, 1778, p. 737 — in: Sigismund Gelenius, Arriani et Hannonis periplus. Plutarchus de fluminibus et montibus. Strabonis epitome, Bas. 1533, p. 203, in 'biblion is', boek 16. |
|
OTI en libuèi hôsper en aithiopiai, tou therous huei pol- la. tou de cheimônos, xèrasia estin. |
| Latijn van Hier. Gemusaeus: Strabonis Geographicorum Lib. XVII (Basel 1539), Epitomae, lib. 17, fol. h2v: "Quod in Africa, quemadmodum in Aethiopia, aestate multum pluit, hyeme siccitas viget."] |
Terugveren en atomenReden van terugspringen ook bij uit atomen samengestelde dingen.Terugspringen of terugbuigen van plaatjes, van luchtballen, is hiervoor [<] door mij zoveel keren opgerakeld dat ik bijna wanhopig was, de reden ervan te kunnen geven met atomen, dat wil zeggen met lichaampjes zonder poriën, bestaande uit minima naturalia [<]. Verder, wat betreft een balletje gevuld met lucht, als het oppervlak ervan tegen de grond wordt geslagen, wordt het naar binnen gebogen, en zo is er binnenin dan meer lichaam dan tevoren. Op dit ingebogen deel van het oppervlak wordt dus meer gedrukt van binnen dan van buiten; want erbinnen leunt, behalve de hele leunende lucht, datgene waarmee de lucht dichter is dan erbuiten. [>] Al kan dan gezegd worden dat de minima van lucht binnenin leeg zijn, als evenwel de zijden van deze minima zich terugtrekken naar binnen, zal dit vacuüm verkleind worden, en zo zal het, doordat het zwaarder is, sneller naar het middelpunt van de Aarde bewegen. En daar er veel van zulke zijn op dezelfde plaats, zal er duidelijk een verschil zijn in de snelheid van daling, wegens het verschil in zwaarte; en daarom kan makkelijk begrepen worden dat de samengeperste lucht naar zijn oorspronkelijke toestand teruggaat, ook als de minima ervan bestaan uit onbuigzame lichaampjes, zoals uit ijzeren ringetjes of haakjes. Want deeltjes die lager zijn en het dichtst bij het middelpunt van de Aarde, zijn slechts gevallen voorzover de leunende lucht erboven ze heeft kunnen samenpersen; als er echter ook een uitwendige kracht bijkomt, worden ze meer samengeperst, en als die weg is, worden ze, daar er gelijk op gedrukt wordt door het omgevende lichaam, naar de oorspronkelijke figuur gevormd, misschien rond of zoiets, en wanneer ze deze hebben gekregen bevatten ze noodzakelijk meer vacuüm. Dus de lucht in een balletje dat tegen de Aarde is geslagen heeft een andere vorm aangenomen; maar de omgevende lucht, die van alle kanten gelijk op het balletje leunt, brengt de oorspronkelijke figuur weer aan. Waarom zou immers op het ene deel van een luchtdeeltje harder gedrukt owrden door een gelijke kracht van de leunende lucht, dan op een ander deel van hetzelfde deeltje? En als dit deeltje de oorspronkelijke figuur heeft gekregen, kan het niet kleiner worden, omdat de zijden hetzelfde blijven, en ze nu in zekere zin dezelfde omtrek beschrijven. LuchtbellenLuchtbellen onder water krijgen een ronde figuur.Hieruit zou misschien ook kunnen worden opgemaakt dat op lucht of water enz. niet meer wordt gedrukt van onder dan van boven*), aangezien er van alle kanten gelijk wordt gedrukt; dus ook op hun vorm. Maar als er een kracht bijkomt, drukt die zonder onderscheid op een luchtdeeltje, het ene deel van het deeltje rakend, terwijl het andere onaangeraakt blijft; waardoor het komt dat het geraakte deel van plaats verandert.
Zo krijgen heel kleine luchtbellen, onder water op hun plaats gehouden, een ronde figuur, maar grote een langwerpige, omdat hetgene dat ze op hun plaats houdt, meer aansluit op de ene zijde dan op de andere. Doch in het algemeen, als een bepaalde taaie en buigzame materie, in zwaarte gelijk aan water, midden in water zou schuilen, zou deze precies een ronde figuur krijgen, daar het water van alle kanten gelijk drukt. *) Tegengestelde mening op p. 157. |
Kleinste deeltje blijft rondMinimum van lucht, uit ronde figuur geduwd, herneemt die meteen.Ook al zou dus een kleinste luchtdeeltje een lege ruimte bevatten, zoals een kaatsbal*), en van dit minimum zouden de zijden bestaan uit draden, bolvormig met elkaar verweven, dan zouden de zijden toch niet naar binnen vallen, maar de bolvorm behouden, daar de overige lucht er van alle kanten op leunt en gelijk op de zijden drukt. Als je namelijk aanneemt dat dit bolvormige minimum door een zekere uitwendige kracht tot een kubusvorm zou zijn gebracht, zeg ik dat het, als die kracht is weggenomen, terstond de bolvorm zal terugkrijgen. Want daar er bij de hoeken meer omtrek is dan in het midden, leunt daarop meer lucht dan op de middens van de vlakken, en daarom (daar alle zijden verbonden zijn) met de hoeken sterk samengedrukt, zullen de middens van de vlakken naar buiten duwen. En als ze niet met elkaar verbonden zouden zijn, maar in veel deeltjes verdeeld, alleen aan elkaar grenzend, zou ongetwijfeld de leunende lucht al die deeltjes naar het middelpunt drijven. Verder, daar alle deeltjes, waaruit dit oppervlak bestaat, aan elkaar zijn vastgebonden als met een soort haakjes, is het zo dat het deel van de bol, dat al begonnen is het dichtst bij het middelpunt te zijn, hol wordt; en daarom leunt er minder lucht op dan op de overige bolle delen die, door meer lucht naar binnen gebracht, met hun stoten de deeltjes van het holle deel naar buiten duwen. Niet anders dan wanneer je een buigzame houten cirkel met de ene hand naar binnen drukt, terwijl de andere hand met meer geweld een ander deel van de cirkel naar binnen drukt. Je zult namelijk zien dat de holte, gemaakt door de eerste hand, wordt verkleind door het geweld van de andere samendrukking, en dat die door de eerste hand samengedrukte zijde teruggaat naar buiten, en zo dus naar buiten wijkt voor het geweld van de tweede samendrukking, die op bolle delen komt.
[ *) Lat.: "pila palmaria", komt voor in een boekje om Latijn te leren: Pieter Afferden, Tyrocinium linguae Latinae, Antw. 1564, p. 51, 'caetsbal'. Later: Thomas Watt, A vocabulary English and Latin, Edinb. 1734, p. 31, 'Hand-Ball' op p. 30.] Magneetpool en wereldpoolWaarom een magneetpool overeenkomt met de wereldpool.De pool van een magneet wijst altijd naar de pool van de wereld, omdat de uit de grote magneet Aarde opstijgende 'spiritus' [<], die delen ervan tegenkomt bij een magneetpool, niet overeenkomt met de poriën die daar zijn. Waardoor het komt dat hij die delen van zich af duwt en als hij de naast bijzijnde poriën binnendringt, niets raakt met één van zijn kanten. En zo verwijdert hij dan die zijde die geraakt wordt, niet anders dan wanneer we een stok schuin in een gat steken; als dit gat nu schuin met de stok overeenkomt, zal het er vervolgens recht tegenover staan. De spiritus duwt en beweegt de beweeglijke magneet dus zolang van zich af, totdat de poriën van de magneet ermee overeenkomen en deze dezelfde stand krijgt als die grote magneet onder de Aarde bezit. Verder van venster: wazigerMet oog van venster verwijderd, worden dingen er waziger door gezien.Dingen van buiten worden door glazen vensters waziger gezien door ogen die hiervan verder verwijderd zijn; maar als de ogen er naartoe worden gebracht, zijn ze duidelijk te bekijken.
Wat niet gebeurt omdat die verder van de ogen af zijn. Want als je het geziene verder van zijn plaats zet dan de ogen van het venster verwijderd waren, zul je niettemin, met de ogen bij het glas gebracht, het ding op grotere afstand duidelijker zien dan een ding dichterbij met de ogen van het glas verwijderd. |
Materie van de stemOf stemmaterie dezelfde lucht is die in de mond van de spreker was.Dat de materie van een stem precies dezelfde lucht is die in de mond van de spreker was, is hiervoor gezegd [<], maar hoe kan dan door schuine gaten een stem beter gehoord worden, dan licht worden gezien? Want als we erkennen dat de materie van een stem lucht is, door lucht van de mond in beweging gebracht en door stroming naar de oren komend, zal niemand zeggen dat lucht moeilijker door schuine gaten gedrukt wordt en stroomt dan water. Maar zijn de minima van de stem soms anders van figuur dan die van licht? Of is het omdat ze van dezelfde aard zijn als de lucht waarin ze vliegen, en ze er makkelijker mee gemengd worden? Of zijn de minima soms groter, die de stem voortbrengen, dan die licht voortbrengen, en daarom beter bestand tegen een groter aantal weerkaatsingen? [>] Waar komt zwaarte vandaan?Waar de zwaarte van lichamen vandaan komt.Dat zware dingen naar beneden willen gaan is niet alleen zeker, maar ook wonderlijk.
Wat als gezegd wordt dat de Zon en de overige hemellichamen hun licht naar de Aarde zenden, en dat dit daar, enige tijd blijvend, stremt en dat het dan door beweging, of voortdurende inwendige werkzaamheid van de Aarde, of door nieuw licht, wegvloeit naar omhoog en onder de Maan het vierde element vormt?
Op deze wijze sleurt de dagelijkse beweging van de Aarde ook de lucht met zich mee, omdat de beweging omlaag niet wordt belemmerd door de cirkelbeweging; daar de lucht, eenmaal in beweging gebracht door de Aarde of door iets anders, voortdurend in een cirkel ronddraait en zonder moeite een bewegend ding volgt. En er zal niet iemand tegenwerpen, als dit gesteld is, dat alles van dag tot dag zwaarder is, omdat de stralen van de Zon meer kunnen doen om alles naar beneden te drukken dan veel vuur. Ik antwoord dat de stralen van de Zon niet zo veel kunnen doen als het vuur dat bevat is onder de kring van de Maan, dat hier dichtbij is, en daarom evenveel sterker dan de Zon als het dichterbij is, met het overige gelijk. Ze werken immers volgens de grootte van de schijnbare oppervlakken, tenzij de Zon ook binnenin brandt, wat toch wegens de afstand niet zou uitmaken voor de kracht van het elementaire vuur als het zo zuiver zou zijn. |
|
Nu is het echter vermengd met veel dampen, en het geeft geen licht en verwarmt niet; toch drukt het niet minder naar beneden dan wanneer het heel zuiver zou zijn. Ja zelfs, als de stralen van de Zon hier niets zouden kunnen doen, welke waarneming zouden we er dan van hebben, daar het alles evenveel zwaarder zou maken? Er zou alleen uit volgen dat een mens 's nachts hoger zou kunnen springen enz. op die manier, aangezien het bij afwezigheid van de Zon de krachten misschien weinig vermindert, en de zwaarte minder. Maar deze beperktheid van springen zal niet blijken. Schippers vertellen echter dat ze hun schip met bomen in de nachtelijke uren verder voortduwen dan overdag: dit heeft één van hen mij verzekerd toen ik 's nachts van Utrecht naar Amsterdam reisde. Maar wegens het eerder gezegde kan de Zon hierbij weinig doen, vergeleken met vuur, en is het nauwelijks waarneembaar. Waarom kan nu die spiritus die uit de Aarde opstijgt niet even goed lichamen optillen? De reden is dat die veel trager opstijgt, en uit grotere deeltjes bestaat, die de poriën van de lichamen niet binnendringen, natuurlijk gaan ze voedsel verschaffen aan vuur. Niet anders dan rook van een vlam (de ene namelijk dik en traag, de andere dun en snel) aan elk deeltje ervan veel voedsel verschaft, daar vuur in veel deeltjes kan worden verdeeld, en vuur in de omgeving werkelijk wordt verdeeld. En misschien hebben donder en bliksem hun kracht nergens anders vandaan dan van de spiritus die met geweld naar beneden daalt, zozeer dat ze torens doen instorten en bomen ontwortelen, enz. [>] |
Beweging van slagadersBeweging van slagaders.Van de beweging van slagaders hebben we eerder gezegd [<] dat die komt van een spiritus die van het hart hun vezels ingaat, en we hebben laten zien op welke wijze ze zo verwijd kunnen worden; en we hebben toen geredeneerd over de spiritus en de fijnheid van de holten en de grofheid van het zicht [<]. Maar als hier iets in de weg staat, wat ik evenwel nog niet zie, moeten we bezien of het hart door zijn aanhoudende beweging het omhulsel van de slagaders niet naar zich toetrekt. Als dit is uitgerekt maakt het ook een wijdere en bolvormige holte; en door het toegankelijk maken daarvan trekken ze van alle kanten aan, om de leegte te vullen met zowel spiritus als bloed. Met één oog verte zienWaarom dingen in de verte met één oog zijn te onderscheiden.Het gezicht onderscheidt verwijdering ook met één oog, omdat de bundel van een verder verwijderd punt een scherpere hoek maakt dan die van een punt dichterbij, wat het netvlies heel gemakkelijk onderscheidt. Het gezicht ontstaat namelijk niet op een mathematisch punt, maar op een fysisch punt, waarmee het de inval ervan, rechter of schuiner, noodzakelijk te voorschijn brengt. Hierdoor komt het dat van afbeeldingen zelfs niet met één oog terstond een levendig beeld en de natuurlijke toestand van de dingen gezien kan worden, daar op een schilderij alle punten van de omtrekken even dichtbij zijn. Het is namelijk nodig door samenknijpen van de ogen het gezicht zwakker te maken en sommige stralen misschien buiten te sluiten, of het netvlies zelf zo te plaatsen, dat punten afzonderlijk worden waargenomen, wat gedaan kan worden door dat naar binnen samen te drukken. Soms zouden dus verder verwijderde punten zwakker geschilderd moeten worden, en zou het verder verwijderde deel van een lijn voorzien moeten worden van wat haartjes. SchilderijHoe we een afbeelding nauwkeurig waarnemen.Van bundels die de breedte van een lijn zouden moeten weergeven bij tekenen op een glas*) of op een schilderij, van de breedte daarvan is de verhouding zodanig, dat die van een verder verwijderd punt groter is; bij het kijken groeit immers de bundel van een punt gelijkmatig tot aan de pupil. Daar dus de verhouding van de afstand van een verder verwijderd punt naar het glas of schilderij, tot de afstand van het glas naar de pupil, groter is dan de verhouding van de afstand van een dichterbij gelegen punt naar het glas, tot de afstand van glas naar pupil (daar deze afstand bij alle punten van de afbeelding dezelfde is), volgt dat de bundel van een verder verwijderd punt op het glas dikker is. (Met één oog heb ik gezien dat de schaduw van een stoel zo is als op een afbeelding waargenomen.) [<,>]
[ *) Hulpmiddel voor perspectivisch tekenen, zoals in de Deursichtighe van Simon Stevin: het glas van Maurits.] |
Of de lucht zwaar leuntOf de lucht zwaar op dingen leunt, met tegenwerping onderzocht.Tegenover de eerste Toegift, of Stelling, bij mijn proefschrift, over de drukkende lucht [<] waarin de reden gegeven wordt voor de vlucht voor vacuüm, heb ik deze tegenwerping gezet die mij een heel uur lang zo sterk leek, dat ik aan een oplossing wanhoopte en het zal het geschiktste argument zijn geweest tegen hen die zich het best verzekerd achten in deze opvatting, of zich er op beroemen (en toch heb ik zulke mensen nog niet gezien), dat zij het voor het eerst, of al vele jaren geleden bedacht hebben. De tegenwerping nu is deze:
Als je een met water gevuld vat op een schaal van de weegschaal zet, en deze door middel van een ander gewicht in evenwicht brengt, vervolgens met een ander vat, omgekeerd in dat water, wat water optilt, terwijl de opening van het tweede vat overal het water raakt en een deel van het water daarin zich in hangende toestand bevindt — Gemakkelijk lijkt immers een antwoord met alleen de vlucht voor vacuüm als eerste beginsel. Van vacuüm wordt immers gezegd dat dit het water aantrekt, en dan omhoog houdt, zodat het op de rest van het water niet meer drukt dan wanneer dit geheel weggehaald zou zijn. Zodat het helemaal geen wonder is dat de rest van het water in het eerste vat minder gewicht heeft, daar een deel ervan niet anders opgetild wordt dan wanneer iemand het lood van de schaal met zijn hand optilt en omhoog houdt. Een werkelijke oplossing geeft ons echter de Statica, die datgene, waarover we ons hier verbazen, aantoont in water. En wie zal betwijfelen dat wat in water gebeurt, ook kan gebeuren in lucht, die dezelfde aard van vloeibaarheid heeft? Die leert dus dat water met meer of minder geweld leunt, afhankelijk van de grotere of kleinere bodem waarop het drukt, als de hoogte gelijk is. Aangezien dus de lucht overal bijna dezelfde hoogte krijgt, komt alleen de bodem in overweging. En de bodem is hier het overige water, waarop de lucht niet sterker leunt dan tevoren, 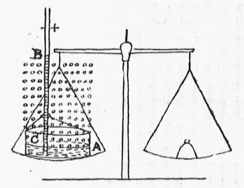 *) Een dergelijk bezwaar werd nog in 1647 gemaakt bij de proeven over het luchtledige te Parijs, zie: C. de Waard, L'expérience barométrique (Thouars, 1936), p. 84, 161.
*) Een dergelijk bezwaar werd nog in 1647 gemaakt bij de proeven over het luchtledige te Parijs, zie: C. de Waard, L'expérience barométrique (Thouars, 1936), p. 84, 161. [ Met deze figuur op p. 161: balans, lood op de rechterschaal, en links 1e vat: A op schaal, 2e vat: buis B (boven dicht!), hangende waterkolom: BC, buitenlucht: stippeltjes, water: streepjes.] |
|
waardoor het komt dat dit deel water niet zwaarder wordt. En toch drukt het, wegens de vloeibaarheid van water, met deze zelfde kracht op alle zijden van het vat en zelfs op de omgekeerde opening van het tweede vat, afhankelijk van de grootte van de bodems of wanden, waarop het water leunt of waaraan het hangt; niet anders, zeg ik, dan een gewicht van duizend pond water op de zijden en de bodem van een kubusvormig vat, een kracht van drieduizend pond levert.*)
[ *) Zie Simon Stevin, Beghinselen des waterwichts, Voorstel X, XI: 1000 pond op de bodem, 4 × 500 pond op de wanden.] Bodem en zijden dragen de lastWaarom bodem en zijden van een vat zo'n grote last water dragen.Wat voor niemand verbazend moet lijken. Elk lichaam is immers zwaar omdat het daalt tot aan het middelpunt van de werreld. En als het verhinderd wordt daarheen te dalen, schraagt een continu of een vast lichaam zichzelf, om niet weg te stromen, door een bepaalde verbinding van de delen onderling. Discontinue lichamen echter die niet zichzelf schragen door een verbinding, dalen ook wel, totdat ze belemmerd worden, en als ze belemmerd worden laat het toe dat delen ervan worden afgescheiden, die hetzij tegen de wanden van een vat leunen, hetzij wegstromen. Deze wegstroming en scheiding van delen zijn niet van belang, zolang ze vrij dalen: dan werken ze immers alleen door zwaarte. Maar als de daling belemmerd wordt, laten ze aan elk deel de eigen zwaarte, waarmee ze zich ook verspreiden naar de zijden door beweeglijkheid in een ronde ruimte. Losse lichamen krijgen dus tweevoudige krachten: de zwaarte van alle delen samen genomen, en de neiging zich af te scheiden door de zwaarte van elk deel apart en de discontiuïteit.
Laten we dus hierna niet meer verbaasd zijn dat er een kracht komt op de wanden van het vat zowel als op de bodem ervan, waarom verwonderen we ons niet eerder erover dat lichamen onderling zo gebonden kunnen zijn, dat ze los niet tegen de wanden stoten.*) *) Hier geeft Beeckman dus een verklaring voor zijn hypothese van de alzijdige voortplanting van druk in vloeistoffen [<], zoals hij voor lucht al veel eerder had gedaan [<]. |
Of gewicht te veranderen isOf het gewicht van dingen vergroot of verkleind kan worden.Gevraagd kan worden of het gewicht van dingen kan worden vergroot zonder enige toevoeging, daar ik eerder heb gezegd [<] dat alles zwaar is naar gelang van de veelheid en grootte van de naar beneden geduwde atomen.
Daarentegen wijst Libavius*) er op dat gebakken bakstenen een groter gewicht hebben dan de ongebakkene, die ook droog wel wat water in zich hebben; maar daar ik denk dat in die eerste vuur is samengegroeid, en dat daardoor de rode kleur wordt veroorzaakt, zegt het niets tegen mij. Maar daar dingen onder water gewogen, lichter of zwaarder kunnen worden naarmate er veel of weinig lucht in besloten is, of erdoor wordt onderschept (op deze manier immers drijven ze soms in water), waarom zouden dan ook niet dingen in lucht gewogen, zwaarder of lichter worden naar gelang van de grote of kleine omvang van onderschept vacuüm? *) Misschien in diens de Pyrotechnia, dat is boek 2 van Commentariorum Alchymiae (Frankfurt 1606), p. 240. [ Gevonden in Andreas Libavius, Defensio et declaratio perspicua alchymiae transmutatoriae (Vesellis 1604), p. 497: "Want gebakken en drogere bakstenen zijn zwaarder dan de ongebakkene die meer vocht hebben." Vergelijk: R. Descartes (vert. J. H. Glazemaker), Brieven, 2e deel (1661), p. 178 (nr. 32, aan Mersenne): "Ik geloof dat de tichelstenen, gebakken zijnde, zwaarder zijn dan als zy niet gebakken zijn".] OlieLichamelijkheid van olie.Het kan ook zo zijn dat twee dingen met hetzelfde gewicht een ongelijke lichamelijkheid hebben. En misschien zou het niet absurd zijn als gezegd zou worden dat olie meer plaats bevochtigt dan water, omdat het meer lichaam heeft, ook al is het lichter dan water. Wat volgens de voorgaande redenen komt, omdat olie meer vacuüm bevat dan water, en de verhouding van het vacuüm in olie tot het vacuüm in water groter is dan die van de lichamelijkheid. En soms is datgene lichter, wat meer lichamelijkheid heeft, door een groot oppervlak. Wat overeenkomt met wat ik hiervoor heb gezegd [<] over het maken van een bol die in lucht opstijgt, omdat er toch enige zwaarte is in de lucht, die de zijden ervan omhoog houdt.
Dus iets dat enige grotere leegtes bevat, met de oorspronkelijke leegtes niet veranderd, doet geen afstand van zijn natuur; maar iets dat de kleinste en natuurlijke leegtes verandert, wordt iets anders. Zo zou misschien goud kunnen ontstaan uit zilver; alle atomen zijn immers van dezelfde natuur, neem aan van zuiver uniforme lichamelijkheid. |
Afbeelding als echt zienAfbeelding zien als de zaak zelf.We zien ook met één oog dat dingen ver weg zijn, zoals ik eerder heb gezegd [<], omdat evenwijdig invallende stralen dan hun samenkomst eerder hebben dan het punt van samenkomst van stralen die schuiner invallen. Deze dingen gebeuren dus omdat er veel stralen weggaan uit een enkel punt en de pupil enige grootte heeft. Daarom, als iemand zich een perspectivische afbeelding naar het leven voorgesteld wil hebben, moet die een oog zo samenknijpen dat ook één pupil wordt verkleind, en dat zo slechts weinig stralen daarin kunnen invallen. Want uit hoe minder stralen de bundel bestaat, des te minder onderscheidt het oog een verschil in verwijdering; ja zelfs: als slechts een enkele straal in een heel kleine pupil zou invallen, zou de herkenning van verwijdering en nabijheid geheel worden weggenomen. Niet anders dan ik heb gesproken over een afbeelding, spreek ik ook over een schaduw, door een kaars of de Zon voorgesteld op een vlak; die toont namelijk de ware gedaante van het perspectief. [>] |
Zeshoekige sneeuwReden van zeshoekige sneeus."Abraham Melis [<] sondt my den 10en April 1623 een hoop huyskens van was, daer de bien haren honich ingeleydt hadden."
Bij de aanblik ervan kwam me in gedachten het onderwerp van de zeshoekige sneeuw*), aangeien ook deze honingraten zeshoekig waren. De reden van zeshoekige sneeuw lijkt deze te zijn. [ *) J. Kepler, De nivis sexangula (1611) wordt later genoemd: T. 3, p. 33. Eerste tekening van een sneeuwkristal: Olaus Magnus (1555) I, p. 37. Meer tekeningen (o.a. van Chr. Huygens) in 'Sneeuwfiguren'. Foto's: Bentley & Humphreys, Snow crystals, 1931, Dover 1962.] |
Verte zienHoe dingen in de verte worden onderscheiden.Dat door ons een verschil in afstand van dingen tot ons wordt herkend, hebben we eerder gehoord [<]: omdat veel stralen die in dezelfde pupil invallen, verschillend samenkomen volgens de grotere of kleinere afstand van de dingen; waaruit we hebben geconcludeerd dat die herkenning er niet zal zijn, als we datzelfde zichtbare punt met slechts een enkele straal hebben waargenomen. Wat we hier bewijzen in zoverre dat dingen die plotseling aan ons verschijnen terwijl we iets anders aan het doen zijn, geen afstand duidelijk maken, daar immers weinig stralen invallen op het netvlies dat op iets anders is gericht, en die juist niet samenkomen op het netvlies, maar dit slechts prikkelen door een enkele draad te raken. Punt niet zo klein als lichtatoomPunt waarvan licht terugkaatst, hoe groot en hoe.Wanneer evenwel sprake is van veel stralen, die uit een zelfde zichtbaar punt weggaan, hebben we het niet over een punt dat zo klein is als een lichtatoom. Want van zo'n punt springt slechts een enkele straal terug, en die wordt teruggekaatst. En het is niet noodzakelijk dat stralen uit zo'n zelfde punt de ogen van alle aanwezigen bereiken, zodat gezicht ontstaat, want ze zien niet allemaal alle punten van deze soort, de een ziet namelijk deze, en de ander die punten, en wegens de veelheid ervan op een heel kleine plek schatten de ogen van alle aanwezigen dat ze hetzelfde punt zien, er zijn immers talloze punten bevat in dit ene punt. En dat het punt waarvan wij denken dat dit het enige is, veel andere punten bevat, blijkt uit die nieuwe kijkers [perspicilla], die voor ons ook lichaamsdelen zichtbaar maken van nooit eerder geziene diertjes, en deeltjes van hun lichaamsdelen [<]. Dus uit zulke punten, ja zelfs nog veel kleinere, bereiken stralen ons. Waarom zou het dan verbazend zijn als gedacht wordt dat de uit zo kleine punten komende stralen uit een enkel punt komen? Zo komen ook afzonderlijke stralen, die in de pupil vallen, uit afzonderlijke punten van het voorwerp. Hoe kan dan, zul je zeggen, die veelbesproken lichtbundel op zoveel manieren uit eenzelfde punt voortkomen?
Ik antwoord: Alle ondeelbare punten, zo dicht bij elkaar dat ze geen verhouding hebben tot de grootte van de pupil, worden voor één voorwerpspunt gehouden. Want al hun stralen komen samen in een enkel beeldpunt op het netvlies achter het oog, omdat ze anders, dat wil zeggen met andere hoeken, invallen op het midden dan op de uitersten van het kristallijne vocht, zodat ze allemaal in één punt samenkomen. Kortom dus: alle stralen die zodanig invallen dat ze naar één punt worden gebroken, worden gehouden voor een enkele straal of een enkel voorwerpspunt. |
ZienManier van zien.Evenwijdig invallende stralen uit een nabij voorwerp worden dus niet opgevangen, omdat het netvlies zich heeft aangepast aan het nabije, en wel zo nabij, dat ze bepaalde hoeken maken. En parallelle, en die welke eerder grotere hoeken maken dan deze opstelling vereist, komen achter het netvlies samen, doelloos en niet opgevangen. En het netvlies past zich aan een of andere opstelling aan, omdat er bij deze afstand zo meer stralen invallen dan anders; dat wil zeggen vanuit het nabije vallen er weinig uit eenzelfde voorwerpspunt evenwijdig in, vanuit iets dat veraf is, de meeste; vanuit iets op gemiddelde afstand gaan de meeste stralen die een bepaalde hoek maken, niet een andere. Want we spannen ons in om alles zo duidelijk mogelijk waar te nemen.
Als er dus, met het oog zodanig opgesteld om een voorwerp duidelijk te zien, op deze wijze te weinig stralen op het netvlies samenkomen, bewegen we dit naar voren, en dan zullen we het voorwerp vager waarnemen, doordat grotere beeldpunten worden gemaakt; maar wel gemakkelijker, omdat een punt van samenkomst op het netvlies nu uit meer stralen bestaat, dan dat punt dat het voorwerp duidelijker weergaf. Den 16en April te Rotterdam. En dat met twee ogen de afstand nog duidelijker wordt waargenomen weet iedereen. Want de ogen staan anders ten opzichte van elkaar wanneer we een punt bekijken dat dichtbij is, dan wanneer het ver weg is. [>] |
Punt op tolWaarom een punt op een draaiende tol een cirkel lijkt, en kleur gekleurder.Eén punt op een draaiende tol lijkt een cirkel, omdat het eenmaal geheel rondgedraaid wordt voordat de indruk van het punt in het oog verdwenen is. [<] En een gebrekkig gekleurde cirkel op een tol in rust lijkt veel sierlijker gekleurd als die omgedraaid wordt, omdat die delen op de cirkel die niet gekleurd waren, wegens de rondwenteling gekleurd lijken. Dan zijn er veel kleine onzichtbare deeltjes waaruit licht voortkomt, die bij het kleuren niet aangeraakt zijn. BuskruitWaarom buskruit zo makkelijk ontstoken wordt.Philosophia naturalis van Sébastien Basso*), bij toeval in mijn handen geraakt, lijkt naar wat ik gezien heb weinig of niets te behandelen dat onverenigbaar is met wat we in dit boek hebben uiteengezet.
Pag. 109, over buskruit dat gemakkelijk wordt ontstoken met uitwendig vuur, en waarom het niet ook door zijn inwendig vuur ontbrandt, geeft niet die wiskundige door mij zo dikwijls ingelaste redenering over de verhouding van oppervlakte en lichamelijkheid [<]. *) Philosophiae naturalis adversus Aristotelem Libri XII ... a Sebastione Bassone, doctore medico (Genève 1621, vignet: 'Amicus Plato, amicus Socrates, sed magis amica Veritas'; herdruk: Amsterdam 1649). Vallende steenEen steen valt in het begin langzamerer dan even later.Basson, pag. 348 berispt Zabarella verkeerd over de toegenomen snelheid van beweging, wanneer een steen valt*).
Wat betreft de vergelijking waarvan hij zegt dat Zabarella die naar voren brengt, erken ik dat daarin een ongelijkheid is, hoewel het ook waar is dat het schip door dezelfde stroom van de rivier in het begin langzamer beweegt dan later. *) Jacopo Zabarella [>], de Rebus naturalibus (Padua 1589) [Ven. 1590, Ff. 1617], met de Motu gravium et levium (Keulen 1594, p. 311). Evenals Basson [p. 353] verklaart hij de versnelling bij het vallen met duwende lucht [1617, p. 307-]. |
|
Dezelfde redenering is er ook in de door hem gecorrigeerde vergelijking. Want hij vergist zich omdat hij niet ziet dat, wanneer het schip al enige tijd in beweging is, die beweging niet vermeerderd wordt. We hebben eerder eens laten zien dat dit gebeurt door teveel weerstand van het water, dat het in korte tijd moet tegenkomen met veel deeltjes die weerstand bieden en bewegen. En we hebben ook laten zien [<] dat dit gebeurt in het geval van een steen, namelijk dat er een punt in de lucht is waarbij, als een vallend lichaam dat heeft bereikt, de beweging ervan niet meer toeneemt, maar het voortdurend zo beweegt tot op de Aarde. En Basson merkt zelf niet op dat een steen in het begin moeilijker alle delen in rust beweegt dan in het tweede moment, wanneer ze zelf ook al beginnen daarheen te gaan, waar de steen zich naartoe haast. En de kracht van de vallende steen kan niet zwakker worden, daar die hem eigen is (of, zoals we eerder [<] hebben gehoord, hij wordt door dezelfde oorzaak omlaag geduwd), maar de neiging naar de Aarde die hij kreeg in het eerste moment, krijgt hij ook in het tweede moment.
"En het is geen wonder dat de hand zwakker wordt, daar hij bewogen wordt door de spiritus die door ons lichaam stroomt".*) En het visje zal onderin het water ongedeerd zijn*), omdat de weerstand door de snelheid van de er in gegooide bol groot is en de bol die beweging niet van zichzelf heeft, maar de beweging neemt steeds af. Dat visje wordt dus door een steen die gewoon wordt ondergedompeld en op eigen kracht daalt, bij de bodem niet minder zwaar gekwetst dan in het bovenste deel van het water. *) Basson p. 351 (1649: p. 316). [De cursief weergegeven zin is geen citaat, maar een opmerking van Beeckman.] En opgeblazen zakken zijn niet zwaarder dan lege, zoals hij beweert*), menend dat die omvang iets bijdraagt tot de zwaarte, omdat de lucht probeert die te verdrijven. Maar als een opgeblazen zak zwaarder lijkt, is dit wegens de dichter gemaakte lucht, of wat vocht, bij het opblazen tegen de wanden gestuit en tot waterige consostentie gebracht. Basson vergist zich dus helemaal. Als namelijk, zoals hij aanneemt, een lichaam wordt verdreven, omdat het heel lastig is voor de lucht, vanwege de grote verdeling, dan zal hoe groter het lichaam is, het des te sneller verdreven worden, en daarom ook dalen. Wat onwaar is. We hebben immers ook laten zien [<] dat van twee lichamen met dezelfde zwaarte het grotere lichaam langzamer daalt, laat staan dat het zwaardere van eenzelfde grootte niet sneller zou dalen. En nog veel absurder is dat hij denkt°) dat een schip in een afstromende rivier vooral door de lucht neergedrukt beweegt, wat water, als het ijs zou zijn, zeker niet zou doen wegens de geringe helling. En als het zou gebeuren, zou het door het gewicht gebeuren. Toch is het niet zo dat het schip het voornaamste deel van de beweging niet van het water ontvangt, wanneer dat ruimer voorhanden is; maar hij denkt dat een schip in weinig water dieper ligt dan in ruim water. *) O.c. p. 352. Aristoteles had dit al beweerd in de Caelo, IV, cap. 4. (1649: p. 317.) °) O.c. p. 356. (1649: p. 321.) [Basson: "Noch lucht, noch water duldt iets vreemds in zich, tenzij gedwongen": een strijd tussen lucht en water, wie duldt het schip? Ondiep water is minder sterk.] |
|
Wat komt door een gebrek aan mechanica en wel de statica. En als hij fouten blijft maken door een gebrek aan wiskunde, zal ik mij ook niet tegenover hem blijven stellen. Al is er nu ook veel geweest over zijn onderzoek over de vorm en over de wereldgeest*), waarbij ik geen zin heb het te onderzoeken, en slechts inderhaast zijn mening te zien.
*) Basson behandelt deze onderwerpen op p. 130-309 en 309-345 (1649: p. 117-278 en 278-311). [Zie index 1621, 1649: Anima mundi, Forma.] BrekenHoe een stok breekt. *)Wat Basson [<] op pag. 379°) enz. zegt over de hefboom, geeft aanleiding drie woorden toe te voegen.
Een stok dus, in een gat geslagen, moet voordat hij daar breekt, ten opzichte van het gat een bepaalde hoek maken met het deel dat in het gat is. En aangezien alle delen van de stok gebogen worden volgens de grootte van die hoek, is het zeker dat een korte stok een grotere buiging ondergaat, dat wil zeggen dat de delen van een kortere stok grotere hoeken met elkaar maken dan die van een langere stok. [ *) Begin van fol. 178bis.r van het manuscript, zie de afbeelding in B.'s handschrift.] °) Van het werk aangehaald hierboven op p. 243. (1649: p. 341-346.) [Philosophia naturalis, 'De motu', Intentio V, Art. III, IV.] 
[ Figuur uit: Galileo Galilei, Discorsi e dimostrazioni matematiche intorno a due nuove scienze (Leiden 1638), p. 114. Transl. H. Crew, A. de Salvio, Dialogues Concerning Two New Sciences (Dover 1914; txt met fig.), Day two: horizontale balk, eenzijdig vastgeklemd, wanneer breekt die door eigen gewicht? Zie ook: Isaac Todhunter (ed. Karl Pearson), A history of the theory of elasticity, vol. 1 (Cambr. 1886), chapter 1.] |