|
dit geldt toch volstrekt niet aan de Hemel; maar objecten die daar onder dezelfde hoek verschijnen worden met de kijker ook in gelijke mate vergroot gezien. Want dat er bij objecten bij ons in de buurt een onderscheid in grootte wordt opgemerkt, komt hierdoor: de uitersten van een object dat dichterbij is, al liggen ze op eenzelfde lijn met de uitersten van een verder verwijderd object, maken niettemin, samenkomend met langere bundeltjes, bij een grotere afstand van de bolle lens een gemeenschappelijke basis op de holle lens, en daarom ondervinden ze een grotere verwijding. Maar in de Hemel, wanneer de Zon, de Maan, en afstanden van twee vaste sterren onder dezelfde hoek worden gezien, en daarom de uiteinden van de middellijnen op dezelfde rechte lijn zijn: omdat alle punten met evenwijdige stralen invallen op de bolle lens, maken ze met kegels van dezelfde lengte, en op dezelfde afstand, een gemeenschappelijke basis op de holle lens, en derhalve vereisen ze een gelijke uitschuiving van de buis, en worden ze met het oog even groot gezien.
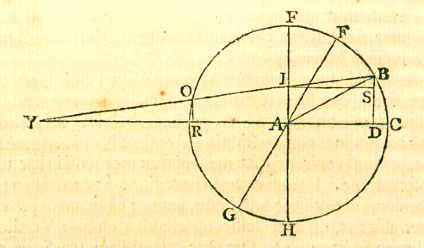
Op zichzelf zijn deze dingen geheel waar, zoals ik heb gezegd. Want dat sommigen zeggen, dat de Maan omdat ze dichter bij ons is, meer wordt vergroot dan afstanden van vaste sterren, is fout volgens Eigenschap I, of moet zo worden begrepen dat de maanschijf, vooral die van de volle Maan, een klein beetje gezwollen in het oog komend, niet wordt ontdaan van al het bijkomstige licht; en dat dit naargelang de gevarieerdheid van de lucht en van de ogen nu eens meer en dan weer minder zichtbaar wordt; zo kan namelijk enige verscheidenheid ontstaan. Maar van de nieuwe Maan, of van de totaal verduisterde bij Eclipsen, wordt de middellijn onder dezelfde hoek aanschouwd als een eraan gelijke afstand van twee vaste sterren, zowel met het blote oog als met de Telescoop; zoals ik me herinner zelf te hebben ondervonden bij de maan-eclips van 8 november 1631 [>], toen bij het midden van de verdonkering de middellijn van de Maan, vrij zichtbaar in een gele kleur, zowel met de kijker in dezelfde stand uitgeschoven, als met het blote oog, gelijk bleek te zijn aan de afstand van de twee sterren B en D in de Plejaden. { Zie de tekening van de Plejaden hieronder }*) Zo worden de Zon en de Maan, met de Kijker binnengelaten, en op een plankje er tegenover opgevangen, en buiten met een Radius°) of ander instrument
[ *) De tekening op p. 52 (hier rechts, verkleind), met daarbij: de Maan was toen in het apogeum, diameter 30'.
|

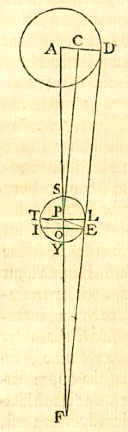 En die wordt als volgt gevonden.
En die wordt als volgt gevonden. 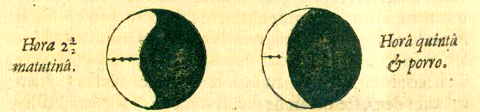

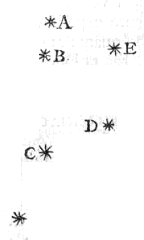


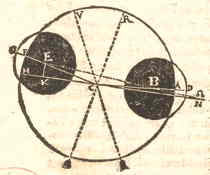
 .
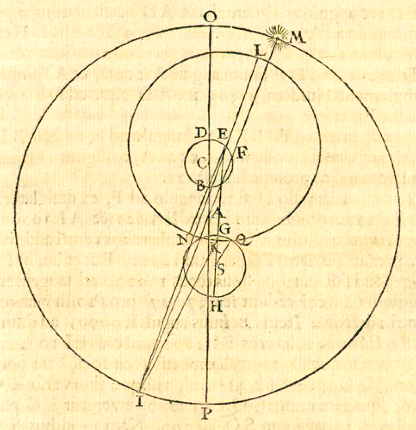
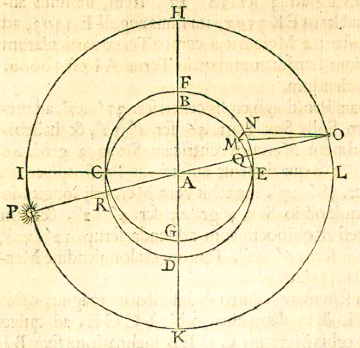
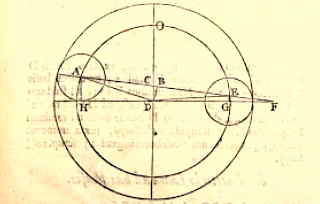
De diameter van Mercurius was van een zeer onbeduidende grootte, en op zijn hoogst 2/3 van de diameter van Venus, als volgt:
.
De diameter van Mercurius was van een zeer onbeduidende grootte, en op zijn hoogst 2/3 van de diameter van Venus, als volgt: