Wij kunnen ons moeilijk indenken, hoe ongelukkig wij zouden zijn, als wij niet de beschikking hadden over onze natuurkundige formules. Wat zouden wij een redeneringen moeten uitvoeren, om een resultaat te vinden, dat met een formule zonder enige moeilijkheid kan worden verkregen. Toch is er een tijd geweest, dat men het zonder formules moest stellen, een tijd, dat de formule nog niet was uitgevonden.   Wij spreken hier niet over formules in de rekenkunde en de meetkunde, maar over die in de natuurkunde en de mechanica, waar de letters grootheden van verschillnde dimensie voorstellen, die met elkaar door wiskundige tekens zijn verbonden, als  s = v × t  en  k = m × a.   Het is wel begrijpelijk, dat er enige durf voor nodig was, ongelijksoortige dingen in een formule te verenigen. Wie heeft dat het eerst gedaan en wanneer is dat geschied? De beantwoording van deze vraag is voor de geschiedenis van het menselijk denken van belang. Kan er een "uitvinder" worden aangewezen? Of is hier van een langzame groei sprake, zodat deze vondst niet op naam van een bepaald persoon kan worden gezet?   Om de tijd, waarin het moet zijn gebeurd, te benaderen, kunnen wij vaststellen, dat aan het einde van de 17e eeuw reeds formules werden gebruikt, en dat men in het begin van die eeuw er nog geen spoor van kan ontdekken. Zo vindt men bij Galilei (1564-1642), de grondlegger van de moderne mechanica, nog geen formules. Laten wij als voorbeeld zijn bewegingsleer eens opslaan. Zoals deze in zijn grote werk, de "Discorsi"*), in 1638 verscheen, was zij reeds lang tevoren door Galilei opgesteld. Waarschijnlijk hebben wij hier met een maar weinig omgewerkt, college-dictaat te doen uit zijn Paduaanse tijd (1592-1610) en is dit geschrift omstreeks 1594 geschreven. In 1634 verscheen het in druk en wel in het Frans door Mersenne verzorgd, waarvan in 1649 een Italiaanse vertaling het licht zag. In de "Discorsi" zijn de stellingen in het Latijn, de tussengesprekken in het Italiaans gesteld. De geleerden in Italië, die beide talen natuurlijk volledig machtig waren, viel dat misschien niet eens op!   We vinden in dit werk de ingewikkeldste stellingen met woorden beredeneerd en dat maakt de zaak voor ons zo onoverzichtelijk. Laten wij een willekeurige stelling citeren: De tijd, waarin een lichaam langs hellende vlakken van verschillende hellingshoek, verschillende lengte en verschillende hoogte omlaag beweegt, is recht evenredig met de lengte en omgekeerd met de wortel uit de hoogte.   Of deze: Als van twee worpbanen (met horizontale beginsnelheid) de sublimatie 1) van de eerste gelijk is aan de hoogte van de andere en omgekeerd, dan zijn de worpverheden gelijk.   Dit zonder formule uit de grondstellingen te moeten afleiden, valt werkelijk niet mee! Het stemt ons kregelig. En Galilei geeft nog ingewikkelder stellingen! Wanneer wij zoiets lezen, beginnen wij met een berekening uit   [ *)  Zie Wikipedia, 'Two New Sciences'. Transl. H. Crew & A. de Salvio, Dialogues concerning two new sciences, 1914.]   1)  Behalve de altitudo, de hoogte, en de amplitudo, de worpverheid, voert Galilei de sublimatio in, waaronder hij de hoogte verstaat, waarover het lichaam vrij zou moeten vallen om als eindsnelheid de snelheid te krijgen, waarmee het horizontaal wordt weggeworpen.

[ 94 ]

formules de stelling te controleren, een hulpmiddel dat Galilei ontbrak, waardoor zijn mechanica nog zo weinig op de onze gelijkt. Wanneer het boek van Galilei in moderne geest zou worden herschreven, zou men met het opstellen van een paar formules beginnen en de rest van de theorie zou eenvoudig in de vorm van vraagstukken volgen.   Bij het ontstaan van de natuurkundige formule dienen wij drie stappen te onderscheiden. De eerste stap is dan hierin te zien, dat men een grootheid door een letter voorstelde, hiermee aangevende dat het mogelijk is, die grootheid door een getal uit te drukken bij het aannemen van een bepaalde eenheid. Dit vindt men reeds bij Aristoteles (384-322 v. Chr.), die in zijn "Physica" bijvoorbeeld een dichtheid, een tijdsverschil, een weg, een kracht, door een letter voorstelt 1). Merkwaardig doet in dit verband de opmerking aan, die L. Defossez in zijn "Les savants du XVIIe siècle et la mesure du temps" (Lausanne 1946 Chap. II pag. 36) maakt:

Aristote n'était pas mathématicien; sa physique ne contient ni figure ni formule et le texte exprime rarement des rapports proportionnels. Quelques formules auraient bien soulagé le texte.

Hier wordt dus als het ware Aristoteles verweten, dat hij geen formules gebruikt. Alsof iemand anders toen reeds op het idee was gekomen, in zo'n geval een formule te gebruiken! De formule moest immers nog worden uitgevonden! De eerste stap, het voorstellen van een grootheid door een letter, heeft Aristoteles juist gedaan. Het is dus eerder zaak hem te prijzen, omdat hij dit begin heeft gemaakt. Hij kan hierdoor, zo niet als de vader, dan toch als de grootvader der formule worden beschouwd.   Een tweede stap is deze, dat het product van twee grootheden in woorden wordt uitgedrukt zonder dat een formule wordt opgeschreven. Laten wij als voorbeeld kiezen het product van een afstand en een kracht, dus wat wij tegenwoordig moment noemen. Reeds Archimedes (287-212 v. Chr.), voor wien de theorie van de hefboom geen geheimen meer had, was in potentie natuurlijk met het begrip moment vertrouwd, al is het regelrechte vermenigvuldigen van een afstand met een kracht van veel later datum. Het woord moment (momentum in de Latijnse, momento in de Italiaanse tekst) komt bij Galilei herhaaldelijk voor, maar dit woord is bij hem niet scherp gedefiniëerd, zoals trouwens in die tijd al dergelijke termen, bijvoorbeeld massa, dat men soms het best door volumen, dan weer als zwaarte, materie, gevaarte of nog anders kan vertalen. Men moet het begrip in de tekst maar "aanvoelen". Bij Galilei is moment zoveel als invloed van een kracht. Zo spreekt hij bij de hefboom (Discorsi, 2e dag) van momentum potentiae (de invloed van de macht) en momentum resistentiae (de invloed van de last).   Wanneer het nu op een plaats lijkt of Galilei het woord moment voor het eerst in de moderne betekenis gebruikt, moet men toch oppassen. Zo zegt hij sprekend van een balk, die horizontaal uit de muur steekt, als hij het gewicht van de balk zelf in rekening wil brengen en gaat beredeneren, dat hij hiervoor de helft van het gewicht aan het uiteinde van de balk kan denken: "Een gewicht aan het uiteinde hangend heeft een dubbel zo groot momentum, als het zou hebben als het in het midden hing". Ook hier doen wij echter beter momentum door invloed te vertalen, naar welke betekenis Galilei in het vervolg van zijn betoog ook weer teruggrijpt.   1)  Men zie in het bijzonder: Lib. IV, Cap. 8, VII, 5 en VIII, 10.

[ 95 ]

Op een andere plaats in de "Discorsi" gebruikt hij het woord momentum voor heel iets anders. Hier heeft hij het over een slinger, die door een pen, loodrecht onder het ophangpunt wordt tegengehouden. Hij betoogt, dat het bolletje telkens even hoog komt, waar de spijker ook zit. Het verkregen momentum is in de omkeerpunten telkens even groot, welk woord hier dus zoveel betekent als hoeveelheid van beweging of kinetische energie of een vaag idee van beide dooreen, waarvoor hij plotseling weer het toen reeds verouderende woord impetus gebruikt.   Voor zover wij hebben kunnen nagaan, is het woord moment het eerst in de nieuwe betekenis gebezigd door John Wallis (1616-1703) in een brief aan Christiaan Huygens (1629-1695) van 1 Januari 1659, waar hij moment noemt het product van een oppervlakte-elementje en een afstand 1). Duidelijker is hij in zijn verhandeling over de Cycloïde van hetzelfde jaar, waar hij zegt 2):

Per momentum autem, tum hic, tum passim alibi, intelligo factum 3) ex magnitudine in distantiam.

(Onder moment echter versta ik hier en overal elders, het product van een grootte en een afstand), maar hij laat er onmiddellijk op volgen "ut quae momentis sunt proportionalia" (als zijnde deze producten met de momenten evenredig). Hij verontschuldigt er zich dus als het ware voor: dergelijke momenten zijn geen producten, maar men kan ze door producten voorstellen, en dan die producten ook wel kortheidshalve "momenten" noemen.   Die aarzeling is er bij Huygens niet meer. 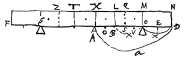Deze schrijft zonder excuus van een "momentum rupturae", dat ontstaat door CD (een stuk van een balk) te vermenigvuldigen met een afstand CE 4). Zowel de brief van Wallis, als zijn verhandeling over de Cycloïde zijn in 1659 gedrukt. Huygens' stuk over het breken van een balk van het jaar 1662, ontleend aan zijn manuscript B is het eerst in 1929 in druk verschenen 5).   Reeds eerder heeft Huygens echter twee grootheden van verschillende dimensie met elkaar vermenigvuldigd, namelijk in 1652 in zijn verhandeling over de botsing 6). Sprekende over de botsing van twee volmaakt harde bollen zegt hij:

Sed necesse est quadrata velocitatum ducta 7) in magnitudinem corporum semper eundem numerum producere

(maar het is noodzakelijk, dat de kwadraten van de snelheden vermenigvuldigd met de grootte der lichamen steeds hetzelfde getal opleveren). Wanneer wij "magnitudo corporis" door "massa" vertalen, wat wel een weinig boud zou zijn, lezen wij hier dat het product mv² constant blijft.   Evenzo lezen wij in Propositio XI van De Motu corporum ex Percussione (Over de beweging van lichamen tengevolge van een botsing), van hetzelfde jaar of iets later, maar niet later dan 1656 8):

Duobus corporibus sibi mutuo occurrentibus, id quod efficitur ducendo singulorum magnitudines in velocitatum suarum quadrata simul additum, ante & post occursum corporum aequale invenitur.

(Wanneer twee lichamen tegen elkaar botsen, wordt   1)  Oeuvres Complètes de Christiaan Huygens, t. II (1889), p. 302.  [txt;  Ned.]   2)  Ibidem, t. XVI (1929), p. 340.  [1659, p. 17.]   3)  Factum = product.   4)  O. C. t. XVI, p. 381.   5)  O. C. t. XVI, p. 381-383.  [ms: HUG 4, 63v]   6)  O. C. t. XVI, p. 95.   7)  Ducere = vermenigvuldigen.   8)  O. C. t. XVI, p. 73.

[ 96 ]

de uitkomst die men verkrijgt, als men de grootte van beide afzonderlijk met de kwadraten van hun snelheden vermenigvuldigd, samenstelt, vóór en na het samentreffen gelijk bevonden). Ook hier hebben wij dus met het product mv² te doen, al is het begrip "massa" nog niet zo scherp gedefiniëerd als thans, maar dat doet aan het feit, dat hier grootheden van verschillende dimensie met elkaar worden vermenigvuldigd, niet af. Deze verhandelingen over de botsing zijn pas in 1703 in de "Opuscula Postuma" in druk verschenen.   Maar reeds eerder is toch al iets van Huygens over de botsing gepubliceerd, namelijk in de "Journal des Sçavans" van 18 Maart 1669, waar we lezen onder "Extrait d'une Letttre de M. Huygens à l'Auteur du Journal; Règles du mouvement dans la rencontre des Corps" 1):

La quantité du mouvement qu'ont deux corps, se peut augmenter ou diminuer par leur rencontre. ... La somme des produits faits de la grandeur de chaque corps dur, multiplié par le quarré de sa vîtesse, est toûjours la mesme devant & apres leur rencontre.

Dit is toch wel een complete formule in woorden!   Maar ook bij Wallis vinden we een formule in woorden. Deze schrijft in een stuk over de botsing in de Philosophical Transactions Numb. 43 [p. 865]. van 11 Januari 1669, dat hij onder "impetus" verstaat "factum ex pondere et celeritate" (het product van het gewicht en de snelheid), wat wij dus, enigszins vrij, als mv kunnen weergeven.   De derde stap is de eigenlijke natuurkundige formule, waarin grootheden van verschillende dimensie door letters uitgedrukt, door wiskundige tekens met elkaar zijn verbonden. Dit vinden wij reeds in een handschrift van Huygens van 1652, waarin wij lezen: bx + ay ac waarin a en b massa's, x, y en c snelheden zijn. De bedoeling is, dat de bol a vóór de botsing een snelheid c heeft, terwijl b rust. Hier vinden wij dus het product mv. Ook mv² komt voor, bijvoorbeeld in de formule axx + byy bcc Dit handschrift is eerst in de Oeuvres Complètes in 1929, dus lang na Huygens' dood verschenen 2).   De eerste gedrukte formules vinden we in het Horologium Oscillatorium (1673), dat waarschijnlijk het eerste gedrukte werk is, waarin natuurkundige formules voorkomen 3).   De uitvinding van de natuurkundige formule is dus eigenlijk niet de daad van één persoon op één ogenblik. Ook hier, zoals overal in de wetenschap, valt een langzame ontwikkeling waar te nemen. Als men de dingen geschiedkundig nagaat, ziet men steeds weer, hoe geleidelijk de begrippen en stellingen tot stand komen. De een sluit zich bij de ander aan; het is als het ware, zoals Pascal zegt: "Le même homme qui pense toujours". Maar toch hebben wij hier met een stap in de ontwikkeling van het denken te doen, een schrede in de voortgang van de wetenschap, en daarom is het wel degelijk van belang, eens na te gaan, wie de eer hiervan toekomt. Voor zover   1)  O. C. t. XVI, p. 179.  [txt]   2)  O. C. t. XVI, p. 98 [handschrift].   3)  Het is wel merkwaardig, dat Huygens zich na 1652 in zijn omstreeks 1656 geschreven "De Motu corporum ex percussione", weer van de formules afwendt.

[ 97 ]

wij hebben kunnen nagaan, was Huygens de eerste, die een werkelijke natuurkundige formule opstelde, een eer, die evenwel tot de wetenschappelijke betekenis van een figuur als Huygens al zeer weinig bijdraagt. Maar het is toch wel merkwaardig, dat dergelijke stappen, waar toch een zekere moed voor nodig is, steeds door de grootsten onder de groten worden gedaan.   Descartes (1596-1650) gebruikt in zijn werken — evenals diverse voorgangers — wel wiskundige formules in de algebra en de meetkunde 1), maar van natuurkundige formules is bij hem nog geen spoor te vinden. Na Huygens wordt de formule meer en meer gebruikelijk in wetenschappelijke betogen. Bij Leibniz (1646-1716) bijvoorbeeld is het voorstellen van physische grootheden door letters al heel gewoon.   Of er reeds door anderen pogingen zijn gedaan om de geschiedenis der natuurkundige formule te schrijven, is ons niet bekend. Dit artikel dient te worden opgevat als een eerste, schuchtere poging in die richting. Mochten onze opmerkingen tot critiek of tegenspraak lokken, dan zijn wij de eersten, die ons daarover zullen verheugen. Wij zijn er van overtuigd, dat de uitvinding van de natuurkundige formule voor de ontwikkeling van het denken en voor de vooruitgang van de wetenschap even belangrijk is als vele ontdekkingen van dezelfde aard, als bijvoorbeeld die van het cijfer nul, de invoering van de decimale getallen, de ontdekking der decimale breuken, de ontwikkeling van de grafische voorstelling en nog vele andere.   Tot slot nog deze opmerking. De invoering van de formule in de natuurkunde is een grote zegen voor de wetenschap, maar zij brengt ook een gevaar mee. Terwijl vroeger te weinig met formules werd gewerkt, komt het tegenwoordig wel voor, dat men meent, de zaak te hebben doorgrond, als deze in formule is gebracht. Een tweede gevaar is hierin gelegen, dat men door het gebruik van een formule tot een onjuiste conclusie kan komen, bijvoorbeeld door ongeoorloofde extrapolatie. Is het nu niet merkwaardig, dat reeds Aristoteles, die de formule nog niet kende, reeds op dit gevaar heeft gewezen?   Hij zegt namelijk 2):

Als A het bewegende, B het bewogene, C de doorlopen afstand en D de gebruikte tijd is, dan zal in dezelfde tijd dezelfde kracht de helft van B over de afstand dubbel zo groot als C bewegen, en over een afstand C in de helft van de tijd D, want zo zal het evenredig zijn. En indien dezelfde kracht hetzelfde ding in een bepaalde tijd over een bepaalde afstand beweegt, dan zal zij ook de helft daarvan in de halve tijd zover brengen en de halve kracht zal de helft in dezelfde tijd over dezelfde afstand verplaatsen ... [Maar] indien de kracht ½A het ding ½B in de tijd D over de afstand C beweegt, dan is het niet noodzakelijk, dat ½A B in dezelfde tijd over ½C beweegt ... Immers, indien het zo uitkomt, zal zij generlei beweging geven.   Als de gehele kracht [het voorwerp] over een bepaalde afstand bewoog, dan zal toch de halve kracht [soms] generlei beweging geven ... Immers één mens zou het schip kunnen bewegen, indien de kracht der schiptrekkers verdeeld mocht worden over hun aantal en over de afstand, waarover zij gezamelijk trokken 3).

1)  Men zie voor de geschiedenis der wiskundige symbolen en formules o.a.: Désiré André, Notations mathématiques, Paris 1909. Florian Cajori, A History of mathematical notations, 2 dln. London 1928 [Vol. 1].   2)  Physica, VII, 5.   3)  Aristoteles heeft klaarblijkelijk in deze gehele paragraaf aan een schip gedacht, dat door het zand naar zee wordt getrokken.