tellen dan wij zelf, die de op- en ondergang van de zon vanaf dezelfde plaats zien. Maar degenen die hier vandaan naar het oosten reizen, tegen de beweging van de wereld in, rekenen één dag als winst; dat dit zo is moet noodzakelijk worden toegeschreven aan de bolling van de aarde.
Daarom is de Aarde bolvormig, en zoals Eratosthenes eens zei:
|
dat ze geheel rond is, echter niet zoals met een draaibank, maar ze heeft enige oneffenheden, *)
|
ze is inderdaad geheel bolvormig, echter niet alsof ze op een draaibank is afgerond, ze heeft immers enige ruwheid, door de oneffenheid van bergen en dalen, niettemin zodanig dat deze in vergelijking met de hele aardbol te verwaarlozen is; zoals hieronder zal worden bewezen.
Zo moet hiermee duidelijk zijn, dat allen die denken dat de aarde zich uitstrekt als een vlakke grond, in zeer grote dwaling verkeren; en niet alleen sommigen van de ouden hebben deze mening gehad, maar van de recenteren verdedigt de niet onaanzienlijke Filosoof Franciscus Patricius°) deze even vasthoudend.
Want dit lijkt ons vooral zo toe wanneer we, in een zeer buitensporige vergelijking, mensjes van onze lichaamsgrootte, of de hoogte van een of andere berg, plaatsend tegenover de hele massa van de aardbol, de blinde gissing van onze ogen volgen en niet het oordeel van de rede. Want de scherpte van de ogen laat ons in de steek, voordat we de zo flauwe bolling van het zo enorme gevaarte met het gezicht kunnen opmerken of waarnemen.#)
Niet anders dan noodzakelijk een vlieg of kever moet overkomen als die op een heel groot wiel zit. Want ook voor ons lijkt op elke cirkel een omtrek van één graad, ook als we heel nauwgezet kijken, bijna uitgestrekt tot een rechte lijn. Zodat, als hun mening iets waars zou hebben, alles voor iedereen tegelijk zou verschijnen; dagen en nachten hetzelfde voor iedereen; of ook zou er geen enkele ongelijkheid van dagen of nachten ergens op de hele wereld gevonden worden. Terwijl nu daarentegen
*) Snellius citeert het Grieks, volgens Strabo, Rerum geographicarum libri XVII, Atrebat. 1587 (Genève; ed. Casaubon, Gr.-Lat.), p. 33, r. 40 (ander ex.).
Deze editie blijkt meestal gebruikt te zijn (zie b.v. p. 69 hierna). Andere editie: Bas. 1549, daar: p. 45, r. 15 van onder (Griekse zin gelijk, Latijn verschillend).
Ed. Meineke (Gr. 1877), 1.3.3; bij Perseus ook: Engl. (transl. Hamilton & Falconer): "that the earth is spheroidal, not however perfectly so, inasmuch as it has certain irregularities".
Eratosthenes' uitspraak staat ook in Nicolaus Amama, Disertationum marinarum decas, Franeker 1651, p. 164, met op p. 165: "Snellius in zijn Eratosthenes Batavus".
°) Franciscus Patricius (1529-1597), Nova de universis philosophia, Ferrara 1591, liber 26, 'Of water en aarde één bol vormen', fol. 132r (txt). Zie ook p. 253 hierna.
Amama 1651 (vorige noot), p. 204-208: 'Betoog van Fr. Patricius over deze kwestie', met uitleg van Patricius' redenering, "Maar nu kan een natuurlijk wateroppervlak niet tegelijk vlak en rond genoemd worden".
Amama (ca. 1618-1656) was leerling van Holwarda (1618-1652) en verzorgde de uitgave van diens Philosophia Naturalis, 1651 en Friesche Sterre-konst, 1652.
#) Zie 'Horizon', 'Platte Aarde', en: 'Offshore windpark'.
Sphaera Joannis de Sacrobosco, Par. 1550, Cap. 6:
"En dat het water een bolling heeft en rondheid nabij komt, blijkt als volgt ..."
Sacrobosco, Cap. 5: 'Dat de aarde rond moet zijn'; Cap. 6: 'Dat het water rond moet zijn'; Cap. 6 (7): 'Dat de aarde het middelpunt van de wereld is', met fig. zodiak.
|



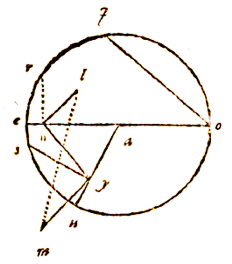
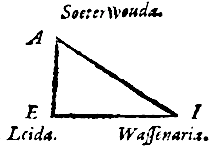
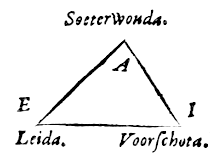
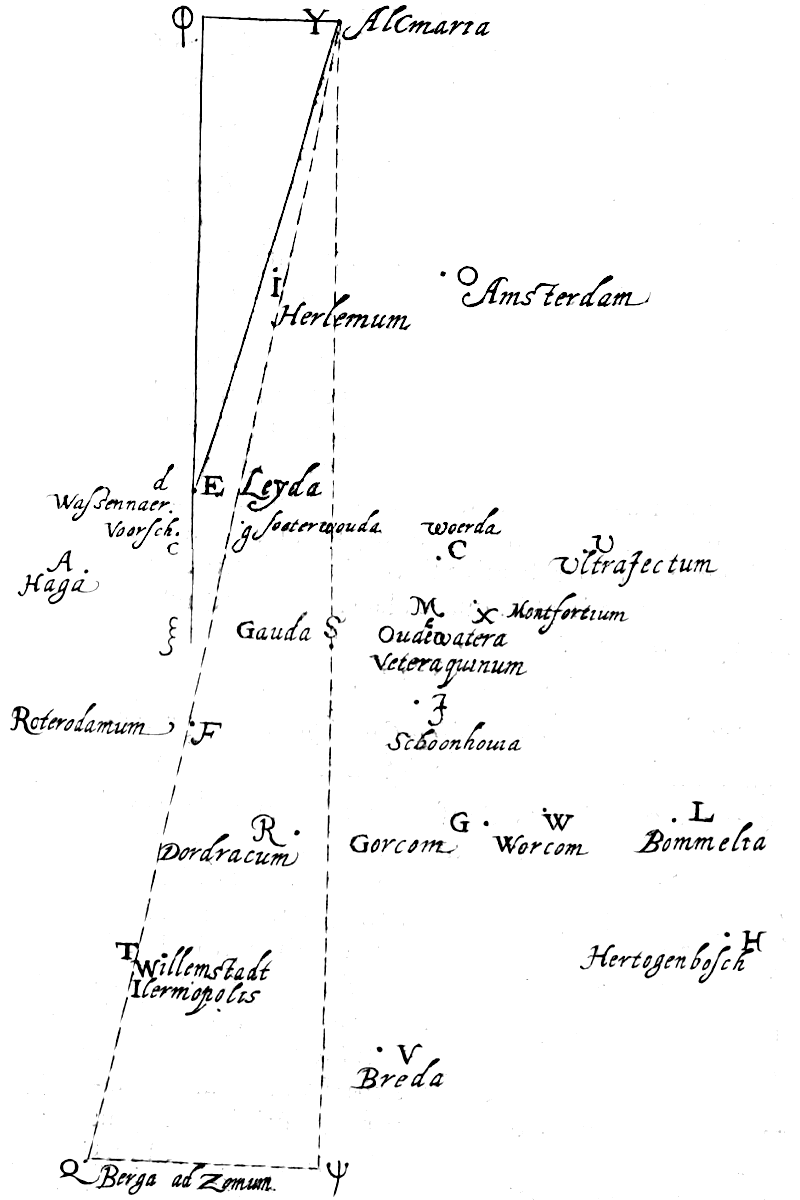
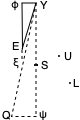
 Laat de twee hoeken eoi en ysu op een omtrek bij hypothese aan elkaar gelijk zijn, en afnemen de omtrekken yu en ei. Ik zeg dat deze omtrekken ook gelijkvormig zijn.
Laat de twee hoeken eoi en ysu op een omtrek bij hypothese aan elkaar gelijk zijn, en afnemen de omtrekken yu en ei. Ik zeg dat deze omtrekken ook gelijkvormig zijn. 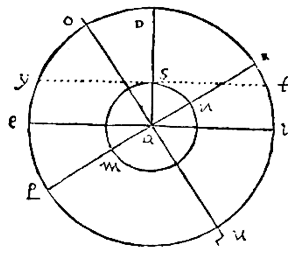
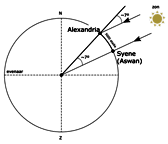
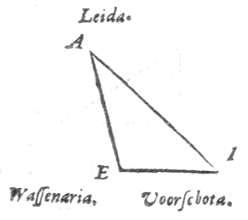
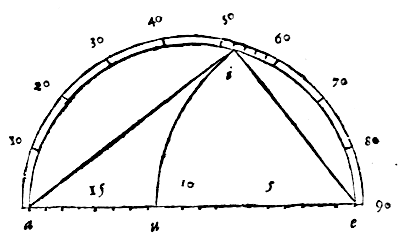
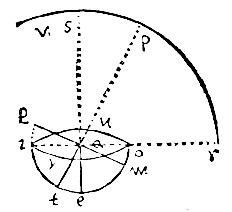 Laat er een holle halve bol ieo zijn, met middelpunt a, en rand iouy als grote cirkel van de halve bol i het vlak van de horizon; de verborgen pool ervan is e met gnomon ae. En neem de grote cirkel ieo als onderste deel van de meridiaan.
Laat er een holle halve bol ieo zijn, met middelpunt a, en rand iouy als grote cirkel van de halve bol i het vlak van de horizon; de verborgen pool ervan is e met gnomon ae. En neem de grote cirkel ieo als onderste deel van de meridiaan. 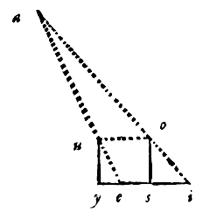
 En om deze reden doen we er dan ook bij elke waarneming met
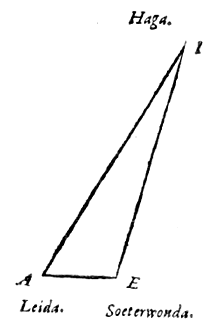
En om deze reden doen we er dan ook bij elke waarneming met 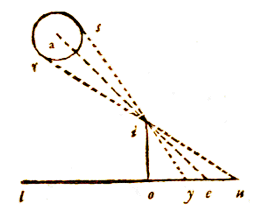 Laat io een gnomon of staaf zijn, loodrecht op de horizon, de schaduw eo. Hiermee wordt nu, zoals boven is aangetoond, de hoek ieo gegeven, die zij rekenden voor de hoogte van de zon. En daar het centrum van de zon over de ecliptica gaat, dachten ze dat ze op de ze manier de hoogte van dat centrum hadden gevonden.
Laat io een gnomon of staaf zijn, loodrecht op de horizon, de schaduw eo. Hiermee wordt nu, zoals boven is aangetoond, de hoek ieo gegeven, die zij rekenden voor de hoogte van de zon. En daar het centrum van de zon over de ecliptica gaat, dachten ze dat ze op de ze manier de hoogte van dat centrum hadden gevonden. 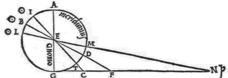

 °) Geoffroy
°) Geoffroy 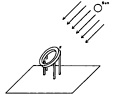



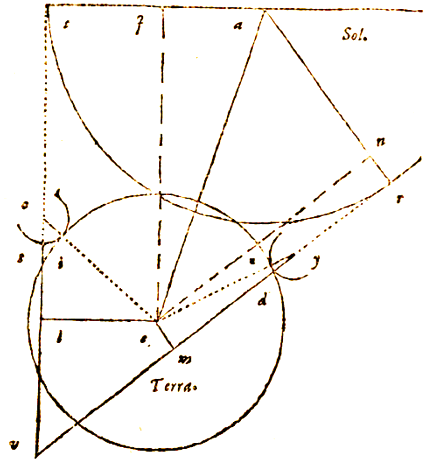
 dat als de Zon voor geen van beide op de loodlijn staat, zoals gewoonlijk bij een winter-zonnewende, uit waarnemingen met een gnomon toch dezelfde afstand tussen beide plaatsen wordt gevonden, als die welke wordt bevonden als de zon voor de ene loodrecht staat.
dat als de Zon voor geen van beide op de loodlijn staat, zoals gewoonlijk bij een winter-zonnewende, uit waarnemingen met een gnomon toch dezelfde afstand tussen beide plaatsen wordt gevonden, als die welke wordt bevonden als de zon voor de ene loodrecht staat. 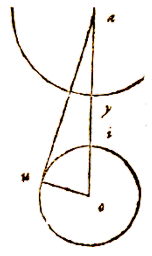 En deze heeft Ptolemaeus, het dichtst bij deze tijd, zo uitgedrukt in zijn grote werk, boek 5, cap. 15*), dat wanneer de halve diameter van de aarde één is, de afstand van de zon tot de aarde 1210 van zulke delen is, en de halve diameter ervan 5. Dit willen we aannemen en gebruiken.
En deze heeft Ptolemaeus, het dichtst bij deze tijd, zo uitgedrukt in zijn grote werk, boek 5, cap. 15*), dat wanneer de halve diameter van de aarde één is, de afstand van de zon tot de aarde 1210 van zulke delen is, en de halve diameter ervan 5. Dit willen we aannemen en gebruiken.  Gegeven zijn dus in driehoek ato de benen to 1 en oa 1210, en hoek aot, daardoor omvat, 7° 30'. Waarmee je met de driehoeksleer kunt concluderen dat hoek tao is: 0° 0' 2" 6/10.
Gegeven zijn dus in driehoek ato de benen to 1 en oa 1210, en hoek aot, daardoor omvat, 7° 30'. Waarmee je met de driehoeksleer kunt concluderen dat hoek tao is: 0° 0' 2" 6/10. 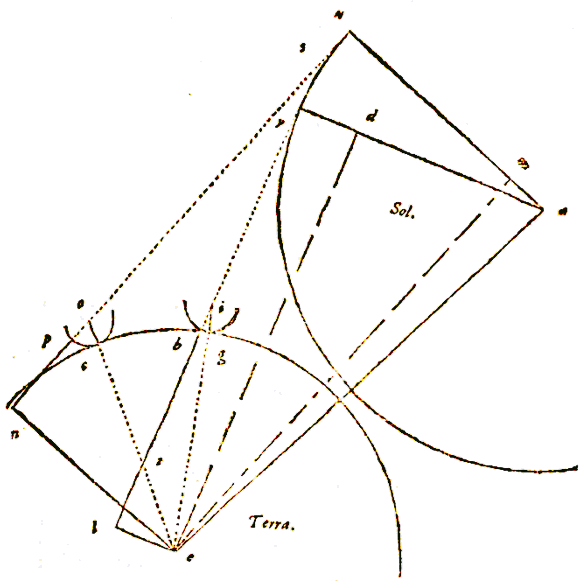
 dat de omtrekken ys en ei volstrekt gelijk zijn; en daarom dat de omtrek ys op aarde eveneens 7° 30' is, dat is, zoals Posidonius zegt, het acht-en-veertigste deel van de grote cirkel yrs op aarde.
dat de omtrekken ys en ei volstrekt gelijk zijn; en daarom dat de omtrek ys op aarde eveneens 7° 30' is, dat is, zoals Posidonius zegt, het acht-en-veertigste deel van de grote cirkel yrs op aarde. 

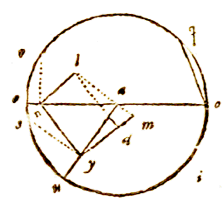
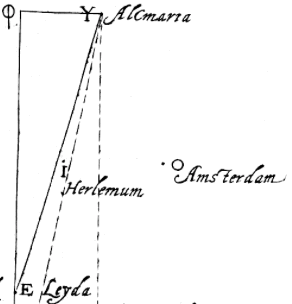
 een massieve sfeer waarvan ae een meridiaan is, en waarvan de vertikale cirkel io die gaat door het zenit van een eerder gegeven plaats en van een tweede plaats, de hoek eio omvat, die genoemd wordt de positiehoek of hellingshoek. Verder is gegeven de breedte van de tweede plaats; dus is de parallelcirkel ervan ook gegeven, en waar deze de positiecirkel snijdt is de ware ligging van de tweede plaats, die in y is.
een massieve sfeer waarvan ae een meridiaan is, en waarvan de vertikale cirkel io die gaat door het zenit van een eerder gegeven plaats en van een tweede plaats, de hoek eio omvat, die genoemd wordt de positiehoek of hellingshoek. Verder is gegeven de breedte van de tweede plaats; dus is de parallelcirkel ervan ook gegeven, en waar deze de positiecirkel snijdt is de ware ligging van de tweede plaats, die in y is. 
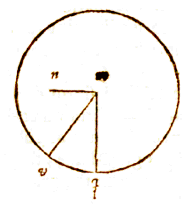 Op een gradenboog*), vastgezet aan iets dat waterpas is met de horizon, wordt een gnomon mn vastgezet, en de eerste grootte van de schaduw mj wordt genoteerd. Waarmee uit de verhouding tot zijn gnomon wordt opgemaakt een zonshoogte van 25° 40'. Dan wordt later, bij een herhaalde waarneming, terwijl de gradenboog op dezelfde plaats blijft, de schaduw vm genoteerd, en uit de grootte daarvan wordt opgemaakt een zonshoogte van 42° 30'. En de hoek vmj door beide schaduwen omvat is 35° 30'. Tenslotte wordt de noordelijke declinatie van de zon gegeven als 14° 20'.
Op een gradenboog*), vastgezet aan iets dat waterpas is met de horizon, wordt een gnomon mn vastgezet, en de eerste grootte van de schaduw mj wordt genoteerd. Waarmee uit de verhouding tot zijn gnomon wordt opgemaakt een zonshoogte van 25° 40'. Dan wordt later, bij een herhaalde waarneming, terwijl de gradenboog op dezelfde plaats blijft, de schaduw vm genoteerd, en uit de grootte daarvan wordt opgemaakt een zonshoogte van 42° 30'. En de hoek vmj door beide schaduwen omvat is 35° 30'. Tenslotte wordt de noordelijke declinatie van de zon gegeven als 14° 20'. 
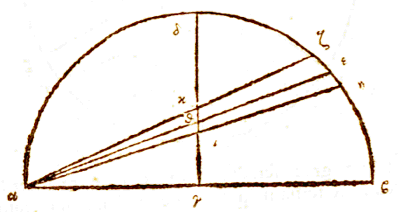

 *) Zie figuur rechts. Driehoek CAD is gelijkvormig met driehoek CEB,
*) Zie figuur rechts. Driehoek CAD is gelijkvormig met driehoek CEB, 

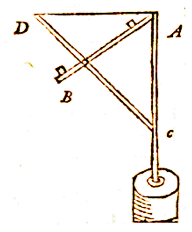 Daarvan was de kleinste, die in nevenstaande figuur met AD wordt aangeduid, en die de zijde van een kwadrant of de halve diameter van een cirkel weergeeft, van 8 voet. Daarom bevatte de dwarslat CD, die de koorde van een kwadrant is, en altijd vast op zijn plaats blijft, een indeling niet alleen in graden, maar ook in afzonderlijke minuten; opdat alle bewerkingen ermee zekerder zouden zijn. Langs deze dwarslat ging tenslotte AB, een andere lat die pinnetjes had.
Daarvan was de kleinste, die in nevenstaande figuur met AD wordt aangeduid, en die de zijde van een kwadrant of de halve diameter van een cirkel weergeeft, van 8 voet. Daarom bevatte de dwarslat CD, die de koorde van een kwadrant is, en altijd vast op zijn plaats blijft, een indeling niet alleen in graden, maar ook in afzonderlijke minuten; opdat alle bewerkingen ermee zekerder zouden zijn. Langs deze dwarslat ging tenslotte AB, een andere lat die pinnetjes had.  Lexander de Macedoniër liet reisdagboeken schrijven door zijn landmeters, de '
Lexander de Macedoniër liet reisdagboeken schrijven door zijn landmeters, de '
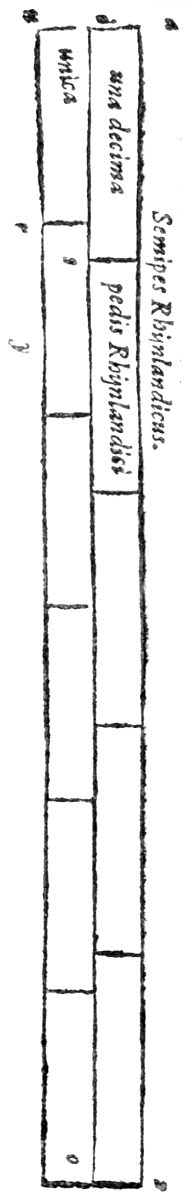 als recentere. De afmeting van onze halve voet heb ik
als recentere. De afmeting van onze halve voet heb ik 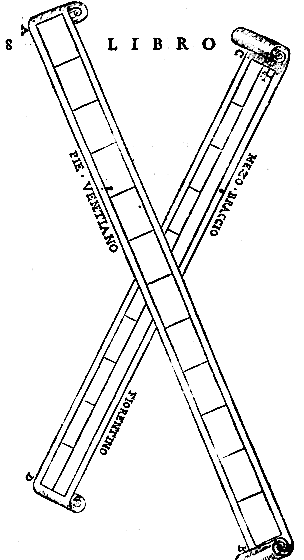




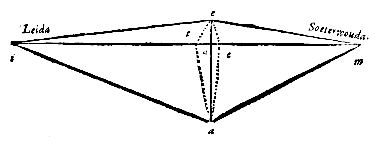
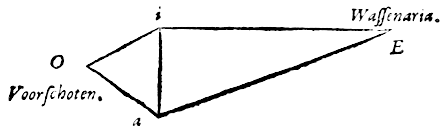
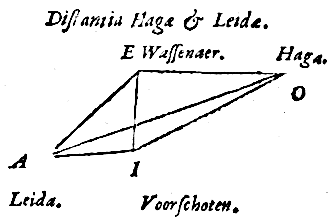




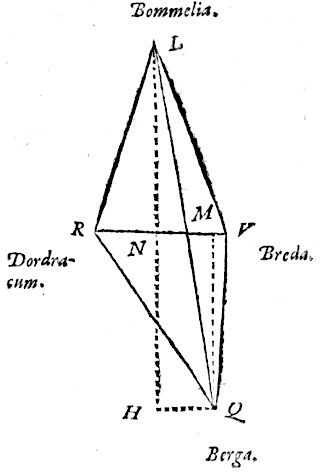

 gelijk zijn aan hoek yoi op de omtrek, die op het tweevoud van zijn omtrek staat. Gegeven is dus hoek yar, en ook gegeven is zijde yi, en daarom het midden ervan, yr. En hiermee zal nu in de rechthoekige driehoek yar, bij gegeven been yr, en hoek yar, te geven zijn het overige been ar en de basis ay van de rechthoekige driehoek.
gelijk zijn aan hoek yoi op de omtrek, die op het tweevoud van zijn omtrek staat. Gegeven is dus hoek yar, en ook gegeven is zijde yi, en daarom het midden ervan, yr. En hiermee zal nu in de rechthoekige driehoek yar, bij gegeven been yr, en hoek yar, te geven zijn het overige been ar en de basis ay van de rechthoekige driehoek. 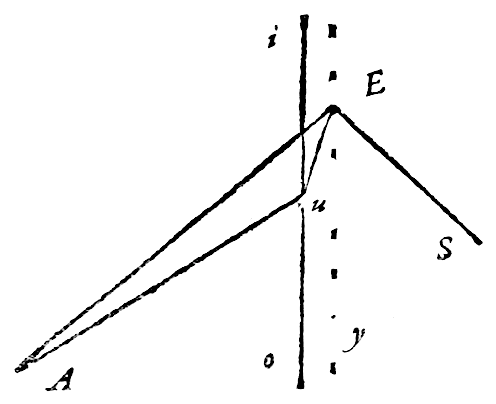
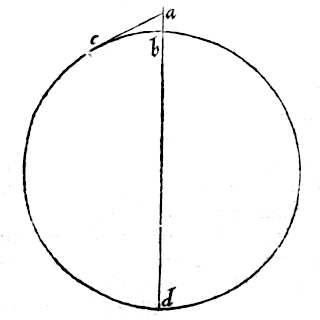
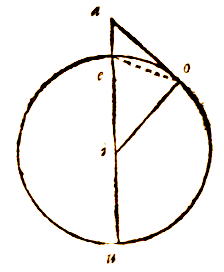 Laat dus ae zijn de hoogte van de berg Etna, ao de lijn die raakt aan de zee; en laat ae zijn de loodlijn, bekend uit waarnemingen. Daarmee wordt, als hoek eao is waargenomen, met kanonieke tabellen van driehoeken gevonden eo; want omdat de omtrek eo over een zo kleine afstand niet afwijkt van een rechte, en ae loodrecht op de horizon staat, zal aeo een rechthoekige driehoek zijn, waarvan het been ae dat immers gegeven is, ook de basis ao zal geven, de rechte die raakt aan de grote cirkel van de aarde.
Laat dus ae zijn de hoogte van de berg Etna, ao de lijn die raakt aan de zee; en laat ae zijn de loodlijn, bekend uit waarnemingen. Daarmee wordt, als hoek eao is waargenomen, met kanonieke tabellen van driehoeken gevonden eo; want omdat de omtrek eo over een zo kleine afstand niet afwijkt van een rechte, en ae loodrecht op de horizon staat, zal aeo een rechthoekige driehoek zijn, waarvan het been ae dat immers gegeven is, ook de basis ao zal geven, de rechte die raakt aan de grote cirkel van de aarde.