[ i ]

[ ii ]

pardon my Presumption, sith it onely proceeds from a great desire I have to serve Your Honour.  In which hopes I assume the boldness to write my self Your Lordships most humble servant. Joseph Moxon.

[ iii ]

To the Reader. T  He many enquiries I have had for Copernican Spheres, hath induced me at last to adventure upon the making them both General and Particular: The General for Demonstration, and the Particular for Operation.   The Diameter of the Starry Orbs are 20 Inches; And the substance of the Circles representing the Orbs, is partly Wood, and partly Brass: The greater Orbs are Wood, and the lesser Brass. The Wooden Orbs are first made into straight thin Riglets curiously glewed close upon one another till they become of a convenient thickness and sufficient strength; and afterwards by Art made into Circles and Orbs: which Circles thus made, do not warp or shrink, as other wooden Circles will; Because the several Riglets binde one another from altering their exact shape: And therefore they are as good for use thus made, as if they were made of Mettal; Nay far more cheap and handy. For were a Sphere made of Brass of 20 Inches Diameter, its price

[ iv ]

(to most) would be unacceptable, and its weight troublesome. These Orbs and Circles are afterwards clothed with Papers printed on Copper Plates, properly Engraved for the purpose. And lastly, the whole is so set together, that with the help of Rundles and Wheels, with great ease and delight all doubts are cleared, and difficulties removed that may hinder the Solution of the Phoenomena by this Hypothesis.   And for your further accommodation, Because these Spheres were never made in England before for general sale, and therefore much unknown; I have writ this Book of the Use of them; wherein I have endeavoured to speak plain to every man's Capacity: And, that I might be the plainer, I have purposely elected most of the same Problemes and Examples, and as neer as I could, the same Terms I did in the Use of the Globes [^]; judging it more easie for a Student to learn what he is somwhat familiar with, than to begin in such manner and matter with which he is not at all acquainted. Farewell, Joseph Moxon.

[ 1 ]

[ 2 ]

In this Systeme is placed the Sun in the Center of the Universe, making a Revolution about its own Center in almost a Moneths time; and about him move concentrically all the other Celestial Bodies, except the Moon, and the Concomitants of Saturn and Jupiter; Next about the Sun moves the Orb of Mercury, which performs a Revolution about the Sun in 80 dayes; Next about Mercury the Orb of Venus, performing its Revolution in nine moneths; Next about Venus the Orb of the Earth and Moon, moving about the Sun in one Year. The Moon being carried about the Earth as a Circle about its Center in 28 dayes; Next about the Eart the Orb of Mars, which moves about in two Years; Next about Mars the Orb of Jupiter, and his four Concomitants, in twelve Years; About Jupiter the Orb of Saturn, and his two Concomitants, in thirty Years: And all these Orbs are included and shut up within one Orb of the fixed Stars; which hath a common Center with all the other Orbs, viz. the Sun, through which Orb the Æquator revolves upon the Axis of the Ecliptick in 25412 Years: And for this cause this Starry Heaven was formerly thought to perform a Revolution in that space of time.   This Hypothesis being look'd upon in Schools

[ 3 ]

as a Novel Intrusion, hath found much opposition: Nor is it a wonder; for Ptolomy's Systeme having for a long time been read to young Pupils, and seeming plausible to Sence, and pleasing to Fancy; hath gained so much favour, and such a general acceptance, that as at first it was their Task to study this Theory, afterwards they thought it their Duty and Interest to defend their Practice, by espousing a Controversie against the Copernicans.   Copernicus himself hath learnedly defended this Hypothesis: And since him, several other Learned Judicious and Serious Persons have done the like: And among the rest, Galilaeus, whose curious scrutiny in Coelestial Speculations, hath with his Telescope discovered such wonderful Appearances among the Heavens to confirm this Hypothesis, that who so lifts but to peruse his Dialogues upon the Systeme of the World, shall therein finde such pure Reason, and concluding Arguments, that undoubtedly he shall close with this Opinion.   Now though my Intensions be only to write the use of these material Spheres, and not to defend the Systeme; for that were an endeavour (as the Vulgar Proverb sayes) to add light to the Sun by setting up a Candle; yet I think it proper in

[ 4 ]

this place to insert some of the strongest Arguments the Ptolemeans bring against this Hypothesis; and also the Answers the Copernicans give unto them.   A R G U M.  I.  Is against the Motion of the Earth: For, say they, We see the Sun, Moon, and Stars rise in the East, make a progress through the South, and set in the West. Therefore our Visual Sense demonstrates they move, not we.   In answer to this we may urge, That the Sense of Seeing is deceitful, and makes that seem to move which stands still; and that stand still which moves: as is often seen upon the Water: For Rowing in a Boat, the Boat shall seem to lie still in the Water, and the Banks of the Shore shall seem to slide away from us: And many times the Moon and Stars shall seem to go along with us which way soever we go.   A R G U M.  2.  Looking round about us, the Heavens appear on each quarter exactly equi-distant from us: Therefore the Earth is in the Center of all the Heavens: For, were it in any other place, we should perceive one part of Heaven neerer to us than another: and the Stars would shew greater on that part of Heaven, which shews neerest to us,

[ 5 ]

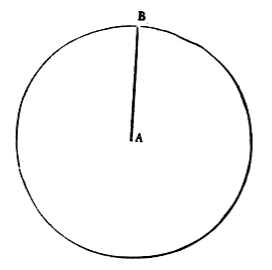
and lesser in that part of Heaven which shews farthest from us.   Answ.  The distance of the Starry Heaven from the Sun, which is the Center of the Starry Heaven, is so vast, and the distance of the Earths Orb so small, that it seems in the very Center it self, and therefore makes in the sight no alteration: as by this following Scheme and Example may be understood.

Imagine this Circle were 20 Inches Diameter, and it represented the Starry Heaven: A is

[ 6 ]

the Center of this Circle; which is on all parts equi-distant from the Circumference. The Line AB (its half Diameter) will then be 10 inches long. Now suppose this Line were divided into 6875 equal parts (for the Semi-diameter of the Starry Heavens contains the Semi-diameter of the Earths Orb 6875 times) and that the Center were removed from its true place one of those equal parts: Then may you first consider the apparent length of one of those parts; and secondly, what difference in appearance from the Center it would have. If the whole length 10 inches be divided into 6875 equal parts, then shall every inch be divided into 687 parts, which is so small a length, that it exceeds not half the bredth of an hair on a mans head, according to a tryal I have made for that purpose: And what difference at the Circumference half a hairs bredth will make from the true Center of a Circle of 20 inches Diameter, is to be considered. It is true, it is a difference from the true Center, but a difference so small, that no man with the Point of a Needle can make a perceptible mark of that size.   Now though the distance of the Earths Orb from the Center of the Starry Heaven be so small that it is scarce discernable by reason of the vast

[ 7 ]

distance of the starry Heaven, yet the distance of the Earths Orb from the Orbs of Mars and Venus is not so great, but that a sensible difference appears at several times in the sight of these Planets: For Mars in his Perigeum, that is, when he is neerest to the Earth, appears sixty times bigger than in his Apogeum, which is his greatest distance from the Earth: And Venus in her Perigeum appears forty times bigger than in her Apogeum; As with the Telescope hath been observed by Galilaeus, and others.   A R G U M.  3.  It is against Reason to think the Earth should turn round; For then we should every Conversion have our Feet turned upwards, and our Heads hanging downwards in the Ayr; Our Houses would tumble over; and every loose thing, as Stones, Animals, &c. fall from the Earth, as having nothing to rest their Weight upon.   Answ.  It is unreasonable to think Nature should Create any thing to its own Destruction; which we must allow, in case the place assigned it by Nature be not apt enough to retain it: for nothing can subsist without a proper place: But we see it customary with Nature to Act beyond Vulgar Reason: For, whether the Earth turn

[ 8 ]

round, or stand fixt in the Center, it matters not in this Argument: For we all allow the Eart to be round, and few men now are so unskilful in the shape of the Earth, as with Lactantius, to deny an Antipodes to every place on the Earth; which Antipodes, according to the reason of this Argument, is as much subject to these Casualties as the whole Earth in its Conversion. Nay, the whole Earth by admitting Antipodes, runs equal hazard of dropping all loose things into the Ayr, as admitting of the Earths Conversion does.   A R G U M.  4.  If according to the Copernican Doctrine the Earth move round from West to East in 24 hours, then admitting the Circumference of the Earth to be 21600 miles, it must in one hour move 900 miles, and in a minute 15 miles, and in the fifth part of a minute 3 miles; so that if a Stone be let fall from a high Steeple, and it be the fifth part of a minute in time falling, which it may be from several Steeples in London, by that time the Stone comes to the ground, the Earth shall have passed from West to East 3 miles; and the Stone must by consequence fall 3 miles to the Westwards of the bottom of the Steeple. To this Argument may be

[ 9 ]

added, that Pidgeons may by strength of their Wings fly three miles to the Westwards from their Dove-house in one quarter of an hour: But in this time should the Dove-house by the Earths motion be preceded Eastwards 225 miles, which with the acquired motion of three miles, makes 228 miles; and then they should alight 228 miles off their Dove-house. Both which Arguments, and several other of the same Nature, Experience contraadicts: Therefore the Earth stands still.   Answ.  By the Earth is not meant only this bare Ball of Earth and Water whereon we inhabite; but the whole Body, as it is clothed with the Elements of Ayr and Fire: For these Elements are frequently convertible into each other: And, as Philosophers teach us, are never so purely one as not to have a mixture of all: Therefore what ever is within this Sphere of Elements, we say is in the Earth, though part of these Elements for their purity be elevated above the Surface of that Soil whereon we go. And therefore when we say the Earth moves, we do not mean onely that part of the Elementary Sphere which we call Earth; But by the Earth we mean the whole Body of Elements, which is

[ 10 ]

according to this Doctrine agitated by one single activity; and what moves in any part of this Sphere, moves in all: As for example; The Stone and the Doves being Elementary Bodies, are inclosed within the Sphere of the Earths Activity, viz. within the Ayr at the highest; and therefore have the Motion imprest upon them that the Earth hath: For which way soever the Stone falls, or is thrown; or which way soever the Pidgeon flies, they move along Eastwards with the Earth, though they fly Westwards. Thus Experience shews, that if a Ship Sails in a swift Motion Westwards, it may in one Second of Time run about three Yards; And if one let fall a Stone from on high into the Hold, that Stone shall not fall three Yards Eastwards from the Perpendicular Point, but just upon the same Point in the Bottome of the Hold it would have fallen if the Ship had layn still, viz. on the Point Perpendicular to the Point above it from whence it was let fall: When as if the Stone had not received the imprest Motion of the Ship, it must have fallen three Yards to the Eastwards of that Point.   A R G U M.  5.  The Earth is a heavie Body, and therefore unfit for Motion, especially through the pure Heavens; for such is

[ 11 ]

the sublimity of them, that the weight of the Earth would press through them; and so it should lose its place.   Answ.  If the Earth be a Heavie Body, yet it is not unfit for Motion, if the moving Power be strong enough to set it going: But heavie Bodies are more unfit to lye still in the sublime Heavens, than to move in them. For thus we shall see a Stone thrown into the Ayr, while it has motion it will abide there; but when the Motion dies, the Stone falls.   Thus briefly have you heard Ptolomy Plaintiff, and Copernicus Defendant (pardon these Law phrases) And you have heard the chiefest Natural Arguments and Answers on either side. The Cause is referr'd to your own Judgements.   Copernicus also has a Plaint against Ptolomy, and brings good Evidence that he traduces the whole Systeme of the World, makes it monstrous, preposterous, deficient, absurd, irregular, unnatural; and in a word, compounded of incongruities: His Witnesses are Sence, Reason, Experiment, and Demonstration: He onely desires an Intelligible Judge, and doubts not but he shall cast Ptolomy. Yet such as are desirous to know what he has to plead, may peruse Himself, Kepler, Bulialdus, Lansbergius, Galilaeus, Helvetius, &c.

[ 12 ]

But Copernicus has not quite cleer'd himself; He must answer another sort of Antagonists: For as of old this Hypothesis was condemned by the Religious men of those Times, who thought it Blasphemy against the Goddess Vesta to deny her the Attribute of Stability; so now many reject it, because they think it against the Doctrine of our Religion; and plead several places of Holy Writ against this Opinion. Object. 1.   And first, to prove the Earths stability, they object that in Psal. 104.5. He set the Earth upon her Foundations, so that it shall never move: And in Psal. 24.2. He hath founded it upon the Seas, and established it upon the Floods: with several other places of the like sence.   Answ.  There is nothing in these Scriptures against the Motion of the Globe of Earth; but enough to ensure us that the Element of the Earth, I mean the Land, shall never move out of the place God hath assigned it: Because it hath its Foundations on the Seas, and there it is established: For neither doth the Psalmist, or any other holy Writer deny, that as it is a Globe, it hath a Motion: But they say, as it is a solid Substance, and Land, it hath its Foundations, &c. And it is plain the Spirit of God in those Texts means the Land, and not the whole Ball Astronomers call

[ 13 ]

Earth, which consists both of Earth, Water, &c. for Moses tells us Gen. 1.10. that God called the dry Land Earth. Object. 2.     Secondly, To prove the Motion of the Sun, they quote Eccles. 1.5 where it is written, The Sun Riseth, and the Sun goeth down, and draweth to the place where he Riseth; Psal. 19. 5,6. where the Psalmist speaking of the Sun, saith, Which cometh forth as a Bridegroom out of his Chamber, and rejoyceth as a mighty man to run his Race: His going out is from the end of the Heaven, and his Compass is unto the ends of the same: with several others to the same purpose.   Answ.  We must not think it the intent of the Spirit of God in these places, or several other, to teach us the Regiment of the Sun; But to set us admiring the Works of the Creation, that so we might be the apter to glorifie him: And to this purpose his Pen-men knew it as advantagious to say the Sun Rises and Sets, as to say the Earth turns about; for it shews equal Power in the Creator, to Ordain the Sun a Motion about the Earth, as to give the Earth a Motion about the Sun. But it better fitted the purpose of those Holy Scribes, for that they in the whole Current of Sacred Scripture writ to the Vulgar Capacities

[ 14 ]

of every man; and therefore chose a plain and familiar Dialect: For thus they frequently represent to us God, as Man, speaking as if his Body were composed of Members, viz. Hands, Arms, Eyes, Ears, &c. And his Mind addicted to Passions, as Anger, Mirth, Sorrow, &c. Not that he is composed of Members, for they knew he is a Spirit; or that he is subject to Passions, for they knew that he is unchangeable, one and the same for ever: But that they might suit their Divine Discourses to Humane Understanding, they tell us Mortals, how God sees and hears all our works and words, as if he had Eyes and Ears: And that Himself will give Reward or Punishment, as if he had Hands and Arms, &c. And that all the Decrees of God, whether Blessings for good Works, or Curses for wicked Works, shall as unavoidably come upon the Godly and the Wicked in due time, as if a Formal Process should gradually prepare the Execution.   Besides, to our sensual appearance the Sun doth Rise and Set, and should the Spirit of God have said the Earth turns about, it might so have confounded Vulgar Understandings, that the Praises, Glory and Honour due unto God, might have been neglected through the Unbelief of that Truth which seems so improbable to our Sense of Seeing.

[ 15 ]

But in brief, As to these Texts, or any other Text in that Sacred Volumn, Take this pithy Answer of St Augustine, quoted by Galilaeus, and thus Englished by Mr Salusbury: If any one shall object the Authority of Sacred Writ against clear and manifest Reason, He that doth so, knows not what he undertakes; for he objects against the Truth, not the Sence of the Scripture, which is beyond his comprehension: Not what is in it, But what finding it in himself he fancied to be in it.   Thus have I done with these Natural and Divine Arguments; I come now to my Primitive Intentions which is, to shew you that Spheres thus made will answer the Appearances of Heaven as well as the Ptolomaick Spheres do: And in Order thereunto, I Present you with Material Spheres, made according to this Hypothesis; And herein I shall first Explain every Part and Lineament in them: And afterwards shew you how to apply them to all the Uses the Ptolomaick Sphere or Globe is to be applyed.

[ 16 ]

C H A P .  I. What a Sphere is. I  N the use of the Globes [1659] I told you, that a Globe was a perfect round Body, contained under one superficies; and a Sphere in a Geometrical Denomination, is the same with a Globe, and is by Mathematicians indifferently called either Globe or Sphere.  But though a Globe or Sphere is, in respect of a Geometrical Body, one and the same, yet as they are both Astronomical Instruments, there is difference between them.  For thus a Globe is an intire whole Body, but a Sphere is fabricated of several Lath-like Circles, so fitted together, that it only serves to represent a whole Body or Orb to the fancy. And the Reason why these Spheres are made of several Circles is, because the whole Systeme of the World consists of several Orbs, the one placed within another; And should any of these Orbs be made of one intire and whole Superficies, unless it were of a transparent matter, it would obscure all the other Orbs within it.   Of these Spheres there are chiefly two sorts invented, the one the Ptolomaick Sphere, and the other the Copernican Sphere.   The Copernican Sphere is the Subject of this Discourse,

[ 17 ]

and is made two several ways, viz. General and Particular : The General is (as it were) a Model of the whole visible World, containing the Starry Heaven, the Planets, their Orbs, Order and Motions about the Sun. So that this Sphere is most apt for Demonstration of this Hypothesis.   The Particular Sphere represents the Sun in the Center of the Starry Heavven, and hath only the Earth moving about it; But is so accommodated with several Circles, that by it may be performed all Questions relating to the Sphere. I intend first to treat of the General Sphere; which that you may the better understand, I shall in the next Chapter describe its Pars. C H A P .  I I. Of the Parts of the General Sphere. The Sun.   I  N the Center of this Sphere is placed a little Golden Ball, which represents the Sun; from the Zenith and Nadir of this Ball runs a Wyer, upwards and downwards, through all the Orbs of this Sphere, and holds them all together at their proper distance from the Sun: Axis of the Ecliptick, North Pole, South Pole.   This Wyer represents the Axis of the Ecliptick: The upper end of it is called the North Pole, the lower end the South Pole. Orb of  Mercury.     Next about the Sun is placed the Orb of Mercury, and is represented by three Circles; two of them stand upwards and downwards, and cut each other at right Angles in the Axis of the Ecliptick; The other Circle cuts them both, and is cut by them both at right Angles in the Plain of the Ecliptick: In the middle of one of the quarters of this Circle stands a small round Ball which represents Mercury, who performs

[ 18 ]

his motion through all the Signs of the Ecliptick in 80 dayes. Orb of  Venus.     Next about Mercury is placed the Orb of Venus, and is also represented by three Circles, as before is said of Mercuries Orb. She performs her motion through all the Signs of the Ecliptick in 9 Months. Orb of the Earth.     Next about Venus is placed the Orb of the Earth, and is also represented by three Circles, as before is said of Mercury and Venus. It is subject to a two-fold motion, besides an Inclination formerly called a Motion. The Earth Subject to a twofold motion, besides an Inclination. The first motion called the Diurnal motion.     The first motion is performed upon its own Axis, from West to East in 24 hours, and is called the Diurnal Revolution : because its turning to the Sun makes Day, and its turning from the Sun makes Night. The second motion called its Annual motion.     Its second motion is its progress through the Signs of the Zodiack, which it performs in 365 dayes: and is therefore called its Annual Motion. Its Inclination     Its Inclination shews how the Poles of the Earth alwayes incline to the same quarter of Heaven, (even as a Needle toucht with a Load-stone doth) and keeps the Axis of the Earth alwayes and in every Degree of the Zodiack parallel to it self. By this Inclination the Seasons of the year are altered; And the Dayes and Nights increase and are diminished. Orb of the Moon.     About the Earth moves the Orb of the Moon, and finishes her course about the Earth in 29 dayes: And though to our apprehensions she seems to run through all the Signs of the Zodiack in that space of time, yet she being carryed about with the Earth, takes up about the same time to run through all the Signs of the Zodiack the Earth doth, viz. 365 dayes: as shall be shewed here-after. Orb of  Mars.     Next about the Orb of the Earth and Moon, is placed the Orb of Mars, and is also represented by

[ 19 ]

three Circles, as before is said of the rest. He finishes his motion through all the Signs of the Zodiack in two years. Orb of  Jupiter.     Next about the Orb of Mars is placed the Orb of Jupiter, and is represented by three Circles as before. He finishes his motion through the Ecliptick in twelve years. Orb of  Saturn.     Next about the Orb of Jupiter is placed the Orb of Saturn, and is represented by three Circles as before; He finishes his motion in 32 years. Orb of the Starry Heaven.     About all these Orbs is framed the Orb of the Starry Heaven, represented by four Circles; two of these Circles stand directly upwards and downwards, and cross each other at right Angles in the Poles of the Ecliptick: These two Circles are called Colures*). That which passes through the Equinoctial signs of Aries and Libra, is called the Equinoctial Colure; And that which passes through the Tropical Signs of Cancer and Capricorn, is called the Tropical Colure. The first of these Colures, viz. that which passes through Aries and Libra, is divided from the middle points between the two Poles both wayes into 90 degrees; so that the whole is divided into four times 90 degrees, and numbred from the middle point into each Pole, with 10, 20, 30. to 90. Solstices.     These two Colures divide the Heavens into four equal parts, which are called Solstices °); The first is a Semi-circle, which passes from the Poles of the Ecliptick through the begining of Aries, and is called the Autumnal Solstice. The second is that Semi-circle which passes from the Poles of the Ecliptick through the begining of Cancer, and is called the Hyemnal Solstice. The third passes through the begining of Libra, and is called the Vernal Solstice. The fourth [ *)  Blaeu (1, 13 and 2, 15): the Colures intersect in the poles of the world (North and South pole), only one of them runs through the poles of the ecliptic.] [ °)  Not a usual name: solstice is the time (in summer and winter) at which the sun appears to pause before returning.]

[ 20 ]

through the begining of Capricorn, and is called the Estival Solstice.   The progress of the Earth through these Solstices, alter the season of the Year; for when the Earth enters the Autumnal Solstice*) Autumn begins; and when it enters the Hyemnal Solstice Winter begins; when it enters the Vernal Solstice Spring begins; and when it enters the Estival Solstice Summer begins. Zodiack.     These two Colures are cut in the middle at right Angles by a broad Circle, representing the Zodiack. In the middle of this Zodiack, on the in-side is a circle described, which is divided into 12. equal parts, called Signs; The first of these Signs begins at the Autumnal Colure [vernal equinox], and is called ARIES, wherein is figured the Picture of a Ram. The second Sign is called TAURUS, wherein is figured the Picture of a Bull. The third GEMINI; and so successively to PISCES, with the proper Pictures in each sign. These Signs are each divided into 30 degrees, and numbred at each tenth with 10, 20, 30. Equinoctial.     These three great Circles are cut obliquely by another great Circle, and makes an Angle with the Ecliptick of 23½ degrees, which represents the Equinoctial: Which is a narrow Circle, and is divided on the inside into 360 degrees, and numbred from the begining of Aries towards Taurus with 10, 20, 30. to 360.   Upon these four great Circles are pictured many Stars, that so the whole Orb may more plainly represent the Starry Heaven. Axis of the Equator.     Twenty three and an half degrees from each Pole of the Ecliptick is fixed upon the Tropical Colure, two small short Wyers opposite to each other, which represents the Axis of the Equator. [ *)  That is: when the sun enters the autumnal equinox (Libra).]

[ 21 ]

These Orbs thus joyned together, are so fitted upon a Pedestal, with a handle to it, that the Axis of the Ecliptick stands directly upwards, cutting the plain of the Ecliptick at right Angles, and passing through the Center of each Orb, and also keeping them at their proper distances.   Yet must we grant that the Diameter of their Orbs and their distances from each other, cannot be truly proportioned in these material Spheres. For the whole Diameter of the Starry Heaven in these Spheres are but about 20 Inches: And could we make the Orb of the Earth so small that it should bear its true proportion to the Starry Heaven, the Diameter of the Earths Orb should be but the 687th. part of an Inch: that is, if you divide an Inch into 687 equal parts, the Diameter of the Earths Orb shall be but one of those parts; as was said in the Preface.   This proportion may be thought fabulous by such as are not much read in Astronomy; especially if they shall consider that it is the Diameter of the Earths Orb: That is, the Circle wherein the Earth moves, and that within it are included the Orbs of the Moon, Venus, Mercury, and the Body of the Sun, and also the Earthly Globe itself; which alone is accounted to be in Diameter 6870. Miles, and yet is but inconsiderable, and as a point to the Earths Orb, as is the Earths Orb to the Starry Heaven; And therefore justly may the Ancients have accounted the Earth, but as a point compared to te whole Fabrick of the Visible World.   This is the frame of the Copernican Systeme: And this Frame will sufficiently serve to represent the Order and Motion of the several Orbs. But notwithstanding the Earth in this Sphere is made so much too big for the Heavens, yet it is so small that what concerns

[ 22 ]

most Problems in Astronomy and Geography, cannot be answered thereby: neither can such proper Circles be applyed thereto, as shall be requisite to demonstrate their operation.   For this cause hath G. Caesius [W. Blaeu] contrived how by the leaving out the Orbs of all the Planets, except the Earth, (as unmaterial) to make the Earth so large, and to furnish it with such apt Circles, as that by his Invention may be resolved all manner of Astronomical and Geographical Questions by this Copernican Sphere, as well as by the Common Celestial and Terrestrial Globes.   But because this Sphere differs in fashion from the Sphere I have just now described; I shall in the next Chapter explain the several parts of it, and afterwards shew how it may be applyed to the several Uses the Celestial and Terrestrial Globes are.

[ 23 ]

Places beyond the Seas. Each of the Months hath its name affixed to it: and each black or white Division signifies one Day, and every tenth Day is numbred at 10, 20, or 30, &c. New stile. Old stile.     That Calender next the outmost verge, is the New-stile, and that next the innermost verge is the Old-stile; and for ornament sake, is adorned with the Pictures of all the twelve Months of the Year. Circle of Signs.     Between these two Calenders, is placed a Circle of the twelve Signs of the Zodiack;  And to each Sign its Character and name affixed. As to Aries, the Character and the word ARIES.  To Taurus, the Character and the word TAURUS. And so all the rest:  Each of these Signs is divided into 30. degrees, and numbred with 10, 20, 30. Moveable Rundle.     Close within the inside of this wooden Circle, is fitted a flat moveable Rundle, whose Center is the same with the common Center.   On the upper plain of this Rundle is sometimes pasted a Projection of the Stars and Constellations about the North Pole; or else some other projection that may better please the fancy; for it is not of any concernment, more than to cloath that naked plain.   The outmost Verge of this moveable Rundle is divided into 24 equal parts, representing the 24 Hours of Day and Night, numbred from the Index towards he right hand, with Numeral Letters thus,  I  II  III  IIII  V, &c. to XII, and then begining again with  I  II, &c. till it end with XII again.   About the Center of the Cross, under this wooden Rundle, is fastened a round Wheel, whose outmost Verge is cut into a certain nimber of Teeth, like those of a Wheel of a Clock: This Wheel lies fixt upon the Cross and moves not.

[ 24 ]

Axis of the Ecliptick.   The Sun.     Through the wooden Rundle, the Wheel on the Cross, and the Cross it self is fitted a Perpendicular Axis whereon the Rundle moves as upon a Center. This Axis represents part of the Eclipticks Axis; and at the top of it is placed a little golden Ball, which represents the Sun.   On the under side of the wooden Rundle moves another Wheel, whose outmost Verge is made with Teeth; and as the Rundle is turned about upon its own Center, this Wheel is also turned about upon its Center, by the falling in of the Teeth on that Wheel fixed on the Cross.   Neer the outmost Limb of the Rundle, is fitted another Wheel, and into this Wheel is fitted a Pedestal, which holds up a Sphere of several Parts, wherein a Terrestrial Globe is inclosed, as shall be shewed hereafter. The outmost Limb of this Wheel is also cut into Teeth; and by the agitation of the two other Wheels, this Wheel is carried about, and with it carries about the Earth, and all the Circles fastned upon the aforesaid Pedestal. Index of the moveable Rundle.     On one side of this Rundle is fastned a little round Pin to turn about the Rundle by, and near to this Pin upon the Rundle, is made an Index which reaches to the outmost Verge of the great hollow wooden Circle, and so at once is applyed to the day in the Month in both Calenders, and also to the degree of the Ecliptick the Sun is in that day; This Index is called the Index of the moveable Rundle. Zodiack.     On each end of the Crosses aforesaid, is placed a Pillar or Column, which serves to support a great wooden Circle representing the Zodiack of the eighth Heaven; in the middle of which on the inside runs a double Line quite round about the whole Circle,

[ 25 ]

which is divided into twelve Signs, and are called, The Signs of the Zodiack; each of which Sign is represented by its proper Character, Figure and Name; As to the Sign Aries, is set the Character, , the picture of a Ram, and the word  A R I E S .  To Taurus the Character, , the picture of a Bull, and the word  T A U R U S ,  and so for all the rest. Each of these Signs is divided into 30 Degrees, and numbred at each tenth, with 10, 20, 30. This great limb is called the Zodiack throughout this Book; and by that name is distinguished from another Circle very like this, called the Ecliptick. Colures.   Poles of the Ecliptick.     Upon the Pedestal that is placed near the outmost limb of the Rundle, is fastned two pretty strong wooden Circles, which cut each other at right Angles: These Circles represent the two Colures [<], and are placed so, that the points where they intersect each other, stand directly upwards and downwards, and represent the Poles of the Ecliptick; the uppermost Pole represents the North Pole, the undermost the South Pole. Equinoctial Colure.  Tropical Colure.   One of these Colures is called the Equinoctial Colure; viz. that which passes through the Equinoctial Signs of Aries and Libra: The other the Tropical Colure; viz. that which passes through the Tropical Signs of Cancer and Capricorn: And this Colure is on the outside divided into 360 Degrees, or which is all one, into four nineties, beginning in the middle between the two Poles; viz. in the plain of the Ecliptick, and so numbred each way, with 10, 20, 30, to 90, which is in the Pole of the Ecliptick. On this Colure is placed a small Hour-Circle about the Axis of the Earth, divided into 24 equal parts, which represent the 24 hours of the day and night, and numbred with numeral letters, thus, I, II, III, IIII, V. to

[ 26 ]

XII; and then beginning again with I, II, III, &c. to XII; till you come to the point where you first began. Ecliptick.     In the middle between the two Poles, is fitted another Circle, which represents the Ecliptick, a good deal broader than the Colures; it cuts the Colures at right Angles, and is by the Colures divided into four quarters; viz. in and ; each of these quarters are divided into three equal parts, which are called Signs, and each of the Signs noted by its proper name, picture and character; as to the Sign Aries, the word Aries, the picture of a Ram, and the character ; to Taurus the like, and so for all the rest: Each of these Signs is divided into 30 Degrees, marked at 10, 20, 30.   On the inner edge of this Ecliptick, is placed several of the most notable fixed Stars, with their names affixed to them, and each Star placed to the degree and minute of Longitude thereon, that it hath in Heaven from the Equinoctial point Aries. Equinoctial.     Oblique to this Ecliptick 23½ degrees on the inside is fitted a thin Circle, representing the Equinoctial; It cuts one Colure in the points of Cancer and Capricorn, and the other Colure, together with the Ecliptick in the Points of Aries and Libra; it is divided into 360 Degrees, and numbred from the Equinoctial Point, Aries, with 10, 20, 30, to 360. Tropicks.     Parallel to the Equinoctial at 23½ Degrees distance on either side are fitted two smaller Circles, representing the Tropicks; that on the North side the Equinoctial, represents the Tropick of Cancer; that on the South side the Equinoctial, represents the Tropick of Capricorn.   On the inside all these Circles in the Poles of the Ecliptick, is fitted two thin semi-Circles (called,

[ 27 ]

Semi-Circles of Latitude.   Semi-Circles of Latitude) so as one of them may move through one half of the Ecliptick; viz. from Cancer through Aries to Capricorn; and the other from Cancer through Libra to Capricorn. These two Semi-Circles of Latitude, may be distinguished one from another, by calling the first of them, The Vernal Semi-Circle of Latitude; because it passes through the Vernal Sign, , and the three Signs on each side of it; and the other the Autumnal Semi-Circle of Latitude, because it passes through the Autumnal Sign , and the three Signs on each side of it; so that these Autumnal Signs lying in the middle of the progress of these Semi-Circles of Latitude, may properly give a name to each Semi-Circle.   At the edge of these Circles, are depicted the same fixed Stars in their proper Latitude, from the Ecliptick Line, that are placed on the Ecliptick Circle aforesaid, with their several names affixed to them. Axis of the Earth.     Through the Solstitial Colure at 23½ Degrees from each Pole of the Ecliptick, passes a Wyer, which represents the Axis of the Earth. On the Northern end of this Axis, is fitted an Index, which serves to point at every hour on an Hour-Circle, which is fitted on the Solstitial Colure, as aforesaid. The Earth.     In the middle of this Axis, between the two Poles of the Ecliptick, is fixed a great round Ball, which represents the Earth, having the bounds of the Lands and Waters depicted thereon, and also the Names of so many Countries and Towns, as can conveniently be placed on a Globe of that Dimension. Horizon.     In two Points of the Equinoctial of this Globe, viz. at 90 Degrees Eastwards from the first Meridian; and in its opposite Point, viz. at 90 Degrees Westwards, are fixed two small Pins, whereon a movable Horizon

[ 28 ]

is placed in the East and West Points thereof, so as those Pins serve for an Axis to the Horizon; for on those Pins the Horizon may be elevated or depressed to any degree the Pole is elevated above the Horizon. Circle of Degrees.     The outmost Limb of this Horizon is devided into twice 180 degrees, beginning in the South Point, and reckoning both Eastwards and Westwards to the North Point, with 10, 0, 30, to 180 degrees. Mariners Compass.     The two next Circles within that Circle of degree, shew the thirty two Winds of the Mariners Compass, each Point of the Compass having its name affixed to it. Antient Winds.     Next within those Circles is a Circle divided into twelve equal parts, according to the manner of the Antients, having the name of each Wind affixed to it, as they were named by them: and in the space between this Circle and the Earth, is emblematically expressed the natural quality of each of these Winds. Meridian.     This Horizon slides on the North and South Points, within a broad Brazen Meridian, hung upon the Axis of the Earth: This Brazen Meridian is divided into 360 degrees, and numbred from the North Pole either way, with 10, 20, 30, to 90 in the Equator; from whence on either side on the Meridian is numbred 10, 20, 30, till it end at 90 in the South Pole.   Round about this Brazen Meridian, on the outmost side, is made a Grove, into which is fitted a small brass Ring, so as the upper side of it lies even with the upper side of the brazen Meridian; this small brass Ring is fastned to two opposite Points in the Horizon, viz. in the North and South, and serves as a spring to keep it to that degree of the Meridian you elevate the Horizon to. Vertical Circles.     Upon two Pins on this small Ring, is also fastned

[ 29 ]

two Semi-Circles of Altitude, or Vertical Circles, yet not so fastned, but that they may move as upon Centers, the one moving from the North to the South through the Eastern side of the Horizon; the other moving from the North to the South, through the Western side the Horizon. Poles of Horizon; viz. Zenith and Nadir.   This motion is performed upon the two Pins aforesaid, as upon two Poles, which indeed they serve to represent (for they represent the Poles of the Horizon) and therefore are so placed, that they may divide the upper and under half the Horizon, into two equal parts, and as the Horizon is moved, slide alwayes into the Zenith and Nadir, and so become the Poles of the Horizon.   These two Semi-Circles of Altitude, are divided each into twice 90 degrees, numbred at the Horizon upwards and downwards, with 10, 20, 30, and ending at 90 in the Zenith and Nadir.   I have already declared the several Uses of each particular Circle herein mentioned in the use of the Globes; whither for brevities sake I refer you, they being with the Globes and Spheres of the same use; and therefore need no further Comments upon them in this place. The End of the First Book.

[ 30 ]

[ 31 ]

Use of the Globes, Book I. And withal, wish he were acquainted with the Use of the Vulgar Globes; because he that understands their Uses perfectly, may much more easily understand the Uses of the Copernican Spheres; for in many Problemes, the Phrases being varied, the Precept is the same in both. As for instance; in the Use of the Globes you are directed to move the Meridian through the Horizon: but by changing the Words of the Precept, you must in the Use of the Sphere, move the Horizon through the Meridian.   Again, you are in the Use of the Globes directed to bring the place of the Sun to the Horizon, or Meridian, &c. and if you apply that Precept, to the Use of the Spheres, you must read, Bring the Horizon or Meridian to the Sun (or which is all one, to the Suns place) because in the Globes, the Horizon is fixt, and the Suns place movable: but in the Spheres, the Suns place is fixt, and the Horizon movable.   3.  Note that in many places where I say, Bring such a Circle, or such a Degree, to the Sun, it is all one as if I had said, Bring it to the Degree the Sun is in in the Ecliptick; for the Sun lying in the Plain of the Ecliptick, the Degree

[ 32 ]

of the Ecliptick the Sun is in, lies just in a straight Line between the Sun and the Center of the Earth; and your Probleme is therefore more practicable, and the answer required, commonly more distinctly found, because of the Suns distance from the Center of the Earth.   4.  Note that when I say, Bring the Meridian to the Sun, or some other place; I mean that Line on the Meridian which is described on the middle of the outermost side between the two edges; for that Line divides he Axis of the Earth exactly into two equal parts: And I also mean that Semi-Circle of the Meridian, which hangs over the first Meridian on the Terrestrial Ball, Because that Semi-Circle alwayes faces the Sun at Noon; and on it, viz. in the Poles of the Horizon is the Zenith alwayes represented in the meeting of the two Vertical Circles.   And when I say, Bring the Horizon, I mean the outermost edge on the upper Plain of the Horizon. And when I name any other Circles or Lines about the Sphere, I mean that Line in those Circles that is graduated; which Line sometimes lies in the middle of the Circle, as in the Equator and Colures it doth; and sometimes on the edge; as in the Vertical semi-Circles, and semi-Circles of Latitude, because that Edge runs into

[ 33 ]

the middle of the Axis of these semi-Circles.   5.  Note that because there is two Circles belonging to the particular Sphere, whereon the Signs of the Ecliptick is depicted, viz. that great one supported by the Bannesters, and that smal one which encompasses the Sphere, wherein the Earth is hung; Therefore, for distinction sake, I shall call the first of them, viz. the great one, The Zodiack; and the small one which encompasses the Sphere of the Earth, The Ecliptick.   Note that in several Problemes, where I say, Make a Mark in such a Line or Circle at such a Degree, to represent any Star, Planet or other Point in Heaven; If that Mark be made with Black-Lead, you may with a little Bread rub it out again when you please, and the Sphere will be never the worse for it.

[ 34 ]

P R O B .   I. How the twofold Motion of the Earth is represented on the Sphere: And how many Miles the Earth moves in any given-time, by vertue of each Motion. T  He Earth has a twofold Motion; viz. a Diurnal, and an Annual Motion; The Diurnal Motion is shewn by turning the Earth about upon its own Axis from West to East: This Motion is performed in 24 hours; as you may see by the Index of the Hour-Circle; for in one Revolution it passes through all the 24 hours on it: and in this Conversion, one part or other of the Earth alwayes stands against the Sun, and the opposite part is alwayes hid from the Sun. In that part which stands directly against the Sun, it is full Noon; and in that part which is most remote from the Sun, it is Midnight; and in all the other parts of the Earth, viz. where the Sun is obliquely beheld in the East, it is Morning; and in those parts where the Sun is obliquely beheld in the West, it is Evening; but in those parts of the Eart that do not at all behold the Sun, it is Night.   Now what measure of space your Habitation moves in any given-Time, by vertue of this Conversion, you shall thus learn to know one degree of Longit. in the Equinoctial contanins 60 English Miles; as was shewn in the Use of the Globes, Book 3. Prob. 10. And the Earth by its Diurnal Conversion, moves 15. deg. in 1 hours time; that is, 900 Miles; and so proportionably for any other measure of Time: But though a Degree of

[ 35 ]

the Equinoctial contain so many Miles, yet doth not a Degree of Longitude in any other Parallel contain so many: for that all Parallels to the Equinoctial grow less and less in a proportion, till they come to the Pole.   Now that you may know how many Miles every Degree of Longitude contains in any Latitude, I have inserted this following Table, where

in the first Column you have the Degree of Latitude, and in the next Column the number of whole Miles and Minutes, or the sixtieth part of a Mile that it contains; so that by seeking the Latitude of your Place in the first Column, the second Column gives you the number of Miles, and Minutes of Miles contained in one degree

[ 36 ]

of Longitude in that Latitude; and by multiplying those Miles by 15, you have the number of Miles, your Habitation moves in one hours time. Example.   I would know how many Miles London moves Eastwards in one hours time; the Latitude of Londen is 51½ degrees; therefore I examine in this Table how many Miles are contained in the degree of Longitude in the Latitude of 51½ degrees: But because this Table is made only for whole degrees, herefore I substract the number of Miles and Minutes contained in a degree of Longitude, in the Latitude of 52 degrees from those contained in the Latitude of 51 degrees; and half that difference I substract from the Miles and Minutes answering to 51 degrees; so shall the Remainder shew (in this case near enough) the Miles and Minutes answerable to 51½ deg. which by this Example is 37 Miles 21 Minutes, or sixtieth parts of a Mile; and this multiplyed by 15, the number of degrees, the Earth turns Eastwards, in one hours time gives 560 Miles 15 Minutes, which is one quarter of a Mile more; so that London moves Eastwards 560¼ Miles in one hours time; and so proportionably for any other Measure of Time.   The Annual Motion is shewn by turning about the Rundle, according to the succession of Signs, till its Index passes through all the Dayes in the Circle of Months. In this Revolution you may see the Earth pass through all the Signs of the Zodiack. And you may also see, that when the Earth is in any Sign, the Sun is seen from the Earth to be in the opposite Sign; as if the Earth enter Aries, the Sun shall in appearance

[ 37 ]

from the Earth, enter Libra: if the Earth enter Cancer, the Sun shall shew as if it entered Capricorn, &c.   By this Revolution, the Dayes and Nights are lengthned or shortned in all places of the Earth, and that according to their scituation on the North or South side the Equator; and the Seasons of the Year are varied into Spring, Summer, Autumn, Winter.   When the Earth is in Southern Signs, the Northern Parts of the Eart have their longest dayes; and when it is in Northern Signs, the Southern Parts of the Earth have their longest dayes; the reason is, because the Earth moves not upon the Poles of the Ecliptick, but upon two Poles 23½ degrees declining from the Poles of the Ecliptick, by which means a greater portion of the Northern half of the Earth faces the Sun, when the Earth is in Southern Signs, than doth when the Earth is in Northern Signs; and therefore makes the Diurnal exceed the Nocturnal Arch, and the Raies (and consequently the heat) of the Sun is more perpendicularly darted on the Northern parts of the Earth then, than when the Sun is in Southern Signs, because the Northern Pole inclines then towards the Sun; and when the Sun is in contrary Signs, it recedes from the Sun; as may be seen by the Sphere.   Now to know what measure of space the Earth moves through the Heavens in any given-time, by vertue of its Annual Motion: you must consider the distance of the Earth from the Sun, which according to the general received opinion, is 604*) Diameters of the Earth; which multiplyed by 6872 (the number of Miles contained in the Earths Diameter) makes 4150688 for the distance in Miles the Earth hath from the Sun, which is half the Diameter of the Earths Orb; this doubled, makes the whole Diameter of the Earths Orb contain 11301376°) Miles. [ *)  Blaeu, p. 31:  571 (diameter of earth's orbit is 1142 earth diameters, according to Tycho Brahe).  Huygens, 1659, p. 80:  distance to sun is 12534 earth diameters.] [ °)  Calculation error,  9301376.]

[ 38 ]

The Diameter of every Circle bears such proportion to the Circumference, as 7 does to 22; therefore the Circumference of the Earths Orb, contains 35518610 Miles; so that in one whole year the Earth running through its Orb, runs 35518610 Miles, which divided by 365, the number of dayes in one year, gives 97311 Miles the Earth runs in one day, which 97311 divided by 24, the number of hours in one day, gives 4054 Miles the Earth runs in one hour: which 4054 divided by 60, the number of Minutes in one hour, gives 67½ Miles the Earth runs in one Minute.   These two motions (viz. the Diurnal and Annual) may aptly be compared to the twofold motion an Iron Bullet has in a Bowl, when Sea-men make Mustard; for as that Bullet runs round the Circumference of the whole Bowl, and also turns round upon its own superficies (as upon its Axis)  So the Earth in its Annual Motion, runs round through the whole Zodiack; and in its Diurnal Motion turns its Superficies round upon its own Axis. [ In the same direction!  With the bullet it is otherwise. ] [ Blaeu, p. 8:  a ball thrown by the hand, rolling along its course ... ] P R O B .   I I Of the Inclination of the Axis of the Earth. N  Otwithstanding this twofold motion aforesaid, yet doth the Axis (and therefore the two Poles) of the Earth respect the same parts of Heaven, and alwayes remains parallel to itself, though the Earth run through all the Signs of the Zodiack. The reason of this Inclination is attributed to some Magnetick Vertue in the Poles of the Earth, which makes them respect

[ 39 ]

alwayes the same part of Heaven; as shall be shewed hereafter when I speak of the Precession of the Equinoctial: I do not say the same Point in Heaven, but the same Part of Heaven; that is, the Axis doth alwayes respect those Stars about the North and South Poles, and hath that small motion formerly attributed to the Starry Heaven.   Now though I told you in the last Probleme, that by the Annual Motion of the Earth, the Dayes and Nights were lengthned and shortned, and the Seasons of the Year altered, yet if the Axis of the Earth did not thus decline, those several Mutations could not happen; for if the Axis of the Earth stood parallel to the Axis of the Ecliptick, the Sun would alwayes be in the Equinoctial, and by consequence, the Dayes and Nights alwayes of equal length: And the temper of the Year in every place of the Earth alwayes in the same condition. [...]

[ 100 ]

[...] P R O B .   L I. Of the Precession of the Equinoctial. I  Have already shewed that the Diurnal Motion of the Earth is a turning towards the Sun, till the Earth make a Revolution upon its own Axis, through all the Degrees of the Equator: And the Annual Motion of the Earth is a turning about the Sun till it hath wholly encompassed it, and in that Motion hath turned every Degree of the Equator upon the Axis of the Ecliptick towards the Sun at Noon; whereby it appears that the Equinoctial performs 365 Revolutions towards the Sun in one year; besides one about the Sun in the same time.   But there is yet another Yearly Motion of 48 Seconds,

[ 101 ]

(according to Mr. Street) attributed to the Equinoctial, which Dr. Gilbert will have depend upon the Earths Magnetick Poles; which Motion is not contiguous to the Earth; but by the Consequences of his Assertion, only inherent to the Magnetick Sphere of the Earth.   This Motion is called, The Precession of the Equinoctial, and might aptly be represented by the Sphere, in case it had a movable Equinoctial, so fitted, that it might slide through the fixt Equinoctial; for then if for every Revolution of the Earth about the Sun, you move the movable Equinoctial 48 Seconds backwards from the Equinoctial Colure, contrary to the succession of Degrees, you would find that in an hundred Revolutions of the Earth (as aforesaid) the movable Equinoctial should be receded 1 deg. 20 min. from the Equinocial Colure; and for two hundred Years, 2 deg. 40 min. and so proportionably the movable Equinoctial would finish a Revolution about the fixt Equinoctial in 27000 years.   This Precession of the Equinox, caused the Antients to conceive a Motion in the Starry Heaven, to be performed from West to East upon the Poles of the Ecliptick; because that by their Observations, they found the Stars alter their Places from the Equinoctial Colure: But such a double Motion is not only improbable, but impossible in Nature, who delights both in ease and uniformity.

[ 102 ]

P R O B .   L I I. Of Tides: And how by helping of the Sphere, you may in general judge of them. D  Ivide the Equinoctial of the Sphere from the intersection of Aries into 30 equal parts; or which is all one, mark every 12 degrees of the Equator with 1, 2, 3, to 30, with Red-Ink; So shall those 30 Divisions represent the 30 dayes of the Moons Age.   Then on the North and South Points of the Compass on the outmost Verge of the Horizon, write with Red-Ink 12.  from the North Eastwards, viz. at the Point North and by East, write 11¼.  at the next Point to that, the same way, viz. North North-East, write 10½.  at the next, viz. North-East and by North, write 9¾.  and so forward to every Point of the Compass, rebating of the last Hour ¾. till you come to 12 in the South, where you must begin again to mark that half the Horizon also in the same order you did the last. In this Circle is then represented the Points of the Compass the Sun and Moon passeth by every day, and the Figures annexed, represent the twice 12 Hours of the Day and Night.   Having thus prepared the Equinoctial and Horizon, you may by having the Moons age, as by Prob. 45. and the Point of the Compass, on which the Moon maketh full Sea at any place given, find at what Hour of Day or Night it shall be high Tide in the same place. Thus.   (It is a known Rule that a North and South Moon makes high water at Margaret.)  Elevate the Poles of the Horizon into the Poles of the Equinoctial; that

[ 103 ]

is, slide the Horizon upwards or downwards, till the Horizon lie just in the Equinoctial: Then bring the North or South Points of the Horizon to the Vernal Colure, and count in the Equinoctial the dayes of the Moons age numbred in red Figures; and the Hour and Minute on the Horizon that stands against the Moons age (also writ in red Figures) is the Hour and Minute of high Tide on that Day at Margaret. [...]

[ 178 ]

[...] F I N I S. T  Hese SPHERES, both General & Particular; Ptolemaick Spheres, GLOBES, Celestial and Terrestrial of all sizes; MAPS for all Countries; SEA-PLATS for all Navigations; The Mathematical Jewel*); The Spiral-Line, and most other Projections, Are made and Sold by the Author, Joseph Moxon, at his Shop on Ludgate-hill near Fleet-Bridge, at the sign of Atlas: Where you may have Books for the use of them; with other Mathematical Books, and Instruments, &c. *)  Astrolabe (image), and:  John Palmer, The catholique planisphaer. : Which Mr Blagrave calleth the mathematical jewel, 1658.

[ 179 ]

Chap. 1.	W	Hat a Sphere is.	fol. 16
Chap. 2.		Of the Parts of the General Sphere.	17
Chap. 3.	An explanation of the several parts of the Particular Sphere.		23  [22]

Prob. 1.	How the twofold motion of the Earth is represented on the Sphere, And how many miles the Earth moves in any given-Time by vertue of each motion.	34
Prob. 2.	Of the Inclinacion of the Axis of the Earth.	38
3.	Of the several Constitutions of the Sphere.	39
4.	The Day of the Month given, To fid the place of the Sun, and the place of the Earth in the Ecliptick.	40
5.	The Day of the Month given, to rectifie the Sphere fit for use in any Latitude, and to set it correspondent to the scituation of Heaven.	41
6.	The Day of the Month given, to find the Declination of the Sun.	43
7.	The Day of the Month given, To find the Right Ascention of the Sun at Noon, and also the Oblique Ascention or Descention of the Sun.	44
8.	The Day of the Month, and Latitude of the Place given, To find the Meridian Altitude.	45
9.	The Latitude of the Place, Day of the Month, and Hour of the Day given, To find the Altitude of the Sun.	46

[ 180 ]

10.	The Day of the Month, the Latitude of the Place, and the Altitude of the Sun given, To find the Hour of the Day.	47
11.	The Day of the Month, and Latitude of the Place given, To find the Amplitude of the Sun, And at what Point of the Compass it Rises.	48
12.	The Day of the Month given, To find the Diurnal and Nocturnal Arch in any given-Latitude.	49
13.	The Day of the Month and Latitude of the Place given, To find what Hour the Sun comes to the East or West Point of the Horizon, And what Almicantur [Almucantar] it then shall have.	50
14.	The Day of the Month, the Latitude of the Place, and Hour of the Day given, To find the Azimuth of the Sun.	52
15.	The Day of the Month, Latitude of the Place, and Hour of the Day given, To find the Almicantar of the Sun.	53
16.	The Day of the Month, and Latitude of the Place given, To find the Hour of the Suns Rising or Setting, And the length of Day and Night.	53
17.	The Day of the Month, and Latitude of your Place given, To find the Beginning, Duration, and ending of Twilight, Morning and Evening.	55
18.	The Day of the Month given, To find what Alteration of Declination the Sun must have to make the Day an hour longer or shorter, And in what number of dayes it will be.	56
19.	To know how much the Pole is raised or depressed where the longest day is an hour longer or shorter than it is in your Habitation.	59
20.	To find in what place of the Earth the Sun is in the Zenith the day and hour given, And also in what several places of the Earth the Sun shall stand in the Horizon at the same Time.	60

[ 181 ]

21.	To know at any given-Time, what a Clock it is in any other part of the Earth.	62
22.	The Day of the Month, and the Meridian Altitude of the Sun given, To find the Elevation of the Pole.	63
23.	The Day of the Month and Altitude of the Sun at East given, To find the heighth of the Pole.	64
24.	How to find the true places of all the Stars on the Sphere, Together with their Longitude and Latitude.	65
25.	To find the Right Ascention of any Star.	67
26.	To find the Declination of any Star.	68
27.	To find the Right Descention, and Oblique Ascention, and the Oblique Descention of any Star in any given-Latitude.	68
28.	The Day of the Month, and hour of the Day or Night given, To find the heighth of any Star above the Horizon in any given-Latitude.	69
29.	The Day of the Month given, To find the time of the Rising & Setting of any Star in any Latitude.	70
30.	To know what Stars neither Rise or Set in any given-Latitude.	71
31.	To find the Difference of Time between the Rising and Setting of any two Stars in any given-Latitude.	72
32.	To find the Cosmical Rising & Setting of the Stars.	74
33.	To find the Acronical Rising & Setting of the Stars.	74
34.	To find the Heliacal Rising & Setting of the Stars.	75
35.	The Meridian Altitude of any Star given, To find the heighth of the Pole.	77
36.	To find what degree of the Ecliptick comes to the Meridian with any given-Star.	78
37.	The Day of the Month, and Hour of the Night given, To know any remarkable Star you see in Heaven in any given-Latitude.	79

[ 182 ]

38.	To find what Day of the Month any given-Star shall at any given-Hour come to any point of the Compass in any given-Latitude.	80
39.	The Day of the Month, and Altitude of any known Star on the East or on the West side the Horizon given, To find the Azimuth and Hour of the Night in any given-Latitude.	81
40.	The Day of the Month, and Azimuth of any known Star given, To find the Hour of the Night and Almicantar of that Star.	83
41.	To find the Hour of the Night by two Stars in the same Azimuth.	84
42.	To find the Hour of the Night by two Stars in the same Almicantar.	86
43.	The Day of the Month given, To find the Hour of the Night by the Rising, Culminating or Setting of any Star.	88
44.	The Day of the Month and Hour of the Night given, To find the heighth of the Pole by a known Star observed Rising or Setting.	89
45.	The Age of the Moon given, To find her Place in the Ecliptick, according to her mean Motion on any given-Day.	90
46.	The Day of the Month and Place of the Moon given, To find the time of the Moons Rising and Setting, and the length of a Moon-shine Night.	92
47.	How Eclipses are demonstrated by the Sphere.	93
48.	To find by the Sphere when an Eclipse of the Moon shall happen.	97
49.	To find by the Sphere when an Eclipse of the Sun shall happen.	98
50.	The Moons Place and the Place of the Dragons-Head or Tail given, to find the Moons Latitude.	99
51.	Of the Precession of the Equinoctial.	100

[ 183 ]

52.	Of Tydes: And how by help of the Sphere you may in general judge of them.	102
53.	To find by the Sphere the Variation of the Needle, commonly called, The Variation of the Compass.	103
54.	To Erect an Astrological Figure of Heaven by the Sphere for any given-Time.	105
55.	To find the length of a Planetary Hour.	111
56.	The length of a Planetary Hour known, To find what Planet reigneth any given-Hour of the Day or Night.	113
57.	To find Part of Fortune [^] by the Sphere.	115
58.	To find in what Circle of Position any Star, or any degree of the Ecliptick is.	116
59.	How to Erect a Figure by the Sphere.	117
60.	Of Revolutions: and how they are found by the Sphere.	119
61.	How a Figure of Heaven may be erected by the Revolution thus found.	120
62.	To make an Equinoctial Dyal in any Latitude.	120
63.	To make an Horizontal Dyal.	123
64.	To make an Erect Direct South Dyal.	128
65.	To make an Erect direct North Dyal.	131
66.	To make an Erect direct East Dyal.	132
67.	To make an Erect direct West Dyal.	136
68.	To make a Polar Dyal.	136
69.	To make Erect North Dyals, declining Eastwards or Westwards.	137
70.	To make a South Erect Dyal, Declinig Eastwards or Westwards.	141
71.	To make Direct Reclining or Inclining Dyals.	142
72.	To make Declining Reclining Dyals.	143
73.	To make a Dyal upon a Declining Inclining Plane.	147
74.	To find in what Place of the Earth any manner of Plane that in your Habitation is not Horizontal, shall be Horizontal.	150

[ 184 ]

75.	To make a Dyal on the Ceeling of a Room, where the direct Beams of the Sun never come.	152
76.	The Leg of a Right Angled Spherical Triangle given, To find the Hypothenusa, and the two other Angles.	157
77.	A Leg and the Hypothenusa given, To find the rest.	160
78.	The Hypothenusa and an Angle given, To find the rest.	161
79.	A Leg and the Angle adjoyning given, To find the rest.	162
80.	A Leg and the Angle opposite given, To find the rest.	163
81.	The Angle given, To find the Sides.	164
Of Oblique Triangles.
82.	The three Sides given, To find the Angles.	168
83.	Two Sides and the Angle contained between them given, To find the rest.	169
84.	Two Sides and an Angle opposite to one of them given, To find the rest.	170
85.	Two Angles and the Side comprehended between them given, To find the rest.	171
86.	Two Angles and a Side opposite to one of them given, To find the rest.	172
87.	Three Angles given, To find the Sides.	173
88.	How to let fall a Perpendicular that shall divide any Oblique Spherical Triangle into two Right Angled Spherical Triangles.	176

This work, 1665 is Moxon's third 'Tutor', the first one (1654) being a translation of Blaeu (1634, part 1); the second one (txt), published in 1659, had many editions. To the Reader (1659): I formerly printed a Book of the Use of the Globes, Intituled A Tutor to Astronomy and Geography: The Book was Composed by William Blaew, but the Title was mine own; and therefore I hope I may be the bolder to use it when and where I list. The sale of that Impression had almost perswaded me to have Printed it again: But when I considered it wanted many necessary Problemes, both in Astronomy, Navigation, Astrology, Dyalling, and the whole Doctrine of Triangles by the Globe; And also that the examples throughout that Book were made for the Citty of Amsterdam ...