T H E O R E M X I:
[ *) Translation from Principal Works, vol. I, p. 175.]
Supposition:
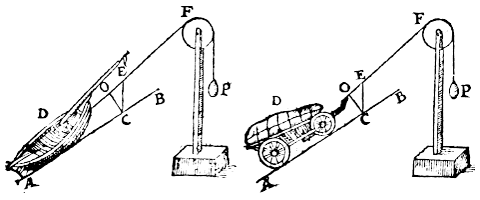
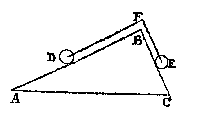
Let ABC be a triangle, whose plane shall be at right angles to the horizon, and the base AC parallel to the horizon,and on the side AB, which shall be double of the side BC, let there lie a sphere D,
and on the side BC a sphere E, of equal weight and equal size to the sphere D.

To prove:
We have to prove that as the side AB (2) is to BC (1), so is the apparent weight of the sphere E to the apparent weight of the sphere D.
Preliminary:
Let us make about the triangle ABC a wreath of fourteen spheres, of equal size and equal weight, and equidistant from one another,as E, F, G, H, I, K, L, M, N, O, P, Q, R, D, all of them strung on a line passing through their centres, in such a way that they can revolve about those centres;
let there also fit two spheres on the side BC and four on BA, i.e. as line to line, so spheres to spheres.
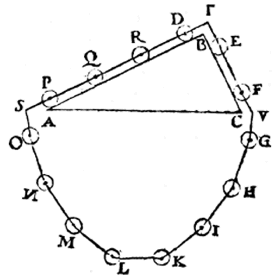
so that if the wreath is pulled down on one side or the other, the spheres roll on the lines AB, BC.

Proof:
If the apparent weight of the four spheres D, R, Q, P were not equal to the apparent weight of the two spheres E, F, either one or the other will be the heavier.Let us suppose (if this were possible) this to be the one of the four spheres D, R, Q, P.
But the four spheres O, N, M, L are of equal weight to the four spheres G, H, I, K.
The side therefore of the eight spheres D, R, Q, P, O, N, M, L is heavier in appearance than the side of the six spheres E, F, G, H, I, K.
But because that which is heavier always preponderates over that which is lighter, the eight spheres will roll downwards and the other six will rise.

But this being so, the wreath of spheres wil! have the same appearance as before,
and on this account the eight spheres on the left side will again have greater apparent weight than the six spheres on the right side,
in consequence of which the eight spheres will again roll down and the other six will rise.
This descent on the one and ascent on the other side will continue for ever, because the cause is always the same, and the spheres will ˆutomatically perform a perpetual motion, which is absurd.

But if from such equal weights there are subtracted equal weights, the remainders will have equal weight.
Let us therefore subtract from the former part the four spheres O, N, M, L, and from the latter part the four spheres G, H, I, K (which are ‘qual to the aforesaid O, N, M, L); then the remainders D, R, Q, P and E, F will be of equal apparent weight.
But the two latter being of equal apparent weight to the four former, E will have twice the apparent weight of D.
As therefore the line BA (2) is to the line BC (1), so is the apparent weight of the sphere E to the apparent weight of the sphere D.
Conclusion:
Given therefore a triangle, whose plane, etc.
[ W: Simon Stevin, law of equilibrium on an inclined plane.]
Corollary 1.
Let ABC be a triangle, as before, whose side AB shall be double of BC, and on AB let there lie a sphere D and on the side BC a sphere E being of equal weight to half of D.
And in F let there be a fixed point, over which the line DFE (to wit, from the centre of the sphere D via F to the centre of the sphere E) can slide, in such a way that DF shall remain parallel to AB, and FE to BC.
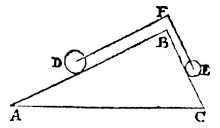
Therefore, as the line AB is to BC, so is the sphere D to the sphere E.
Corollary 2.
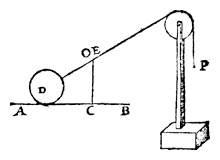
Now let us put one side of the triangle, as BC (AB being double of it) at right angles to AC, as in the annexed figure.
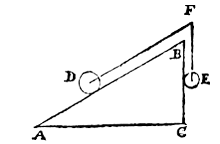
Corollary 3.
Let us now put in the place of the point F a pulley*), as shown in the annexed figure, in such a way that the oblique lifting line from D to F shall remain parallel to AB.
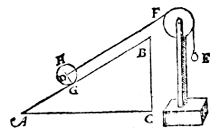
Therefore, as AB is to BC, so is the sphere D to the weight E.
Corollary 4.
Since the sphere of the 3rd corollary touches the line AB in the point G as fixed point, the axis GH will be at right angles to AB.
Therefore let us take away the sphere, and put in its place the prism D, of equal weight to the sphere, in such a way. that the axis GH (its fixed point being G) shall be at right angles to AB, and the oblique lifting line between D, F still parallel to AB and meeting the side of the prism in I, as shown in the annexed figure.
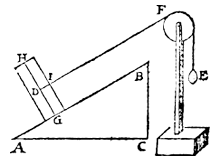
[ *) How to make a pulley: Weeghdaet, p. 17, PW, I, p. 321.]
Corollary 5. Let us draw the vertical from the centre of the prism D, as DK, meeting the
side of the prism in L.
This being so, the triangle LDI is similar to the triangle ABC, for the angles ACB and LID are right angles, and LD is parallel to BC, and DI to AB.
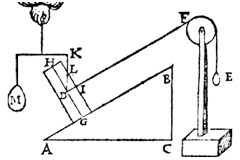
Let us now attach at the line KD the vertical lifting weight M of equal apparent weight to the prism. This weight M will be of equal weight to the prism, by the 14th proposition. Therefore, as LD is to Dl, so is M to E.
Corollary 6. Let us draw BN, meeting AC produced in N; in the same way DO, meeting LI produced, that is the side of the prism, in O, and in such a way that the angle IDO shall be equal to the angle CBN.
Let us also attach at DO the oblique lifting weight P, which shall keep the prism (the weights M and E being taken away) in that position.
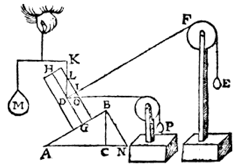
The above may also be understood of a sphere lying on a line AB, as shown in the annexed figure, in which case we say, as before, as LD is to DO, so is M to P (to wit: if CL is drawn at right angles to AB, i.e. parallel to the axis GH of the sphere D).
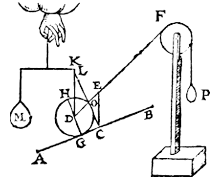
But because LD and DO cannot easily be drawn in practice inside the body of the sphere, let us draw the vertical CE; we shall then have outside the said body a triangle CEO similar to the triangle LDO, the homologous sides of which triangles are LD to CE, and DO to EO.
Therefore, as LD is to DO, so is CE to EO;
and consequently: as CE is to EO, so is the weight of the sphere to P.
Now for the sake of greater clearness let us put this separately, without the other lines, as shown in the annexed figure,
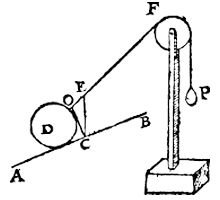
And this is true not only of spheres, but also of other solids sliding or rolling on points or lines, as shown below (a subject with which we will deal more properly in the Practice of Weighing), where we still say: as CE is to EO, so is the weight of the solid D to the weight P.