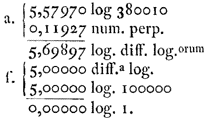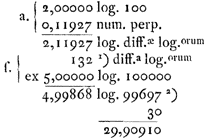IV. 1662.   17 Jul. 1662. Over de hoogte van de atmosfeer 1).   In het Torricelliaanse experiment is de hoogte van het Kwikzilver in de buis, wanneer deze goed luchtledig is gemaakt, door Boyle gevonden van 2 voet 6 Londense duim, of van 30 inch 2). Deze kwikhoogte weegt natuurlijk op tegen een kolom lucht tot aan het buitenste van de atmosfeer, als de dikte van de kolom gelijk is aan de middellijn van de buis. Nu is de verhouding van de zwaarte van Kwik tot water ten naaste bij die van 13 4/7 tot 1 3), waaruit volgt dat de kolom water die opweegt tegen de genoemde 30 inch kwik of de luchtkolom, een hoogte zal hebben van ongeveer 34 voet. Anderzijds is de verhouding van de zwaarte van lucht tot water door mij gevonden als ongeveer van 1 tot 960 4). Van lucht namelijk zoals die hier is samengeperst. Dus zou een hoogte van 32640 voet met zo samengeperste lucht opwegen tegen 34 voet water, of 30 inch kwik, zo groot wordt immers de hoogte als 960 met 34 wordt vermenigvuldigd. Doch laten we het ronde getal van 33000 voet nemen.   1)  [Zie 'Voorbericht'.]  Dit stuk ... [Hug 4, f48r-50r] volgt na dat van 16 juli over kwadratering van de hyperbool met behulp van logaritmen. Een recentere versie verschilt nogal ... [Hug 13, f14r-17r], zie App. I, p. 491-494.   2)  Dit staat in Exp. 36 van New experiments physico-mechanicall, 1660 [p. 298: "near about thirty Inches"] ... In Exp. 17 [p. 128]: "30 Inches and above an eighth".   3)  Boyle had in Exp. 36 gevonden 13 19/28 [1660, p. 296].   4)  Zie brief aan Lodewijk, 22 febr. 1662, T. IV, p. 64. De experimenten (20 febr.) ... [Hug 4, 28v, T. XVII, p. 329].

[ 484 ]

Verder is met Boyleaanse experimenten bevonden dat de ruimten die door eenzelfde hoeveelheid lucht worden ingenomen de omgekeerde verhouding aanhouden van de gewichten waarmee erop gedrukt wordt 1). Zo zal, als er op een deeltje lucht, in een glazen buis opgesloten, 60 inch kwik drukt, deze lucht tweemaal zo weinig ruimte innemen als wanneer er maar 30 inch kwik op drukt. Waarbij evenwel steeds ook de zwaarte van de lucht in acht moet worden genomen, zoals immers lucht die in een buis zit, als er geen kwik is bijgegoten, toch zo moet worden beschouwd alsof er door 30 inch kwik op wordt gedrukt, omdat het gewicht van de lucht die boven ons staat zoveel is. Maar wanneer er 30 inch kwik is ingedaan, is aan te nemen dat er als het ware door 60 inch op wordt gedrukt. We bedoelen inches van de Londense voet, maar niet van zwaarte*). Met dit dus zo gesteld kan alles worden uitgelegd wat betrekking heeft op de hoogte van de Atmosfeer, en de verschillende dichtheid van lucht in welke regio ervan dan ook.   Laten we stellen dat een of andere kolom lucht, vanaf het laagste van de aarde tot het hoogste van de atmosfeer, door horizontale sneden verdeeld is in heel kleine delen waarvan elk een gelijke hoeveelheid en gewicht aan lucht bevat, waarbij duidelijk is dat deze delen een zeer ongelijke uitrekking zullen hebben, aangezien hoe hoger een deel is, hoe minder gewicht van de lucht het draagt en hoe meer het zich dus uitrekt. 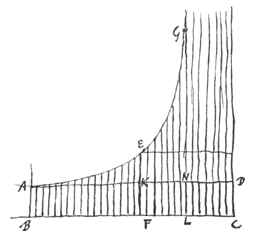De gelijke hoeveelheden lucht in deze delen kunnen worden aangeduid met de gelijke deeltjes waarin de rechthoek ABCD is verdeeld. Waarvan het deeltje het dichtst bij AB weergeeft het onderste deeltje lucht, en elk van het volgende de volgende luchtdeeltjes in dezelfde volgorde. Als nu de rechte AB weergeeft de hoogte tot waar het onderste luchtdeeltje zich uitstrekt, dan zal gemakkelijk ook de uitstrekking van de overige worden gevonden.°) Laten we immers zo'n willekeurig luchtdeeltje beschouwen zoals FK; daar dit slechts het gewicht draagt van de overige die de rechthoek KFCD uitmaken, zal het zich bijgevolg zoveel verder uitbreiden dan het onderste deeltje bij AB, als de deeltjes in de hele rechthoek ABCD zwaarder zijn dan die in rechthoek KFCD.   1)  Huygens ontving bericht van Moray in een brief van 13 maart 1662 (T. IV, p. 84-85). Na kennis te hebben genomen van Boyle's A defence of the doctrine touching the spring and weight of the air (T. IV, p. 171, n. 2) was Huygens overtuigd, aan Moray schreef hij op 14 juli 1662 (ibid.): "Ik was vooral heel blij er de twee experimenten te vinden betreffende verdichting en verdunning van lucht, die deze opmerkelijke eigenschap duidelijk genoeg bewijzen, te weten dat zijn veerkracht gaat volgens de omgekeerde verhouding van de ruimte waarin hij gebracht wordt".   [ *)  Het Latijnse 'uncia' (1/12 deel) is 'inch' geworden, maar ook (troy) 'ounce'.]   [ °)  ABCD telt 34 vakjes: de genoemde waterkolom van 34 voet in stukjes van 1 voet; nu met lucht i.p.v. water.]

[ 485 ]

Dat wil zeggen zoals BC tot CF, zo zal hoogte EF van de uitrekking van deeltje KF zijn tot AB, de hoogte van uitrekking van het onderste deeltje. Dus rechthoek AB.BC zal gelijk zijn aan rechthoek EF.FC, en daarom ligt het punt E op de hyperbool die beschreven wordt door punt A, met BC en CD als asymptoten. Van elk apart bepaalt dus de hyperbool AEG de uitrekking, naargelang de volgorde waarin ze in rechthoek ABCD worden getoond; en zoals EF de uitrekking is van deeltje KF, zo is GL de uitrekking van deeltje NL en zo ook bij de andere.   Nu maken de uitrekkingen van alle die in rechthoek ABFK bevat zijn samen de ruimte AEFB, en van alle in rechthoek ABLN maken de uitrekkingen de ruimte AEGLB. En wel zo: hoeveel maal groter bijvoorbeeld de ruimte AEGLB is dan rechthoek ABLN, zoveel maal groter zal de hoogte zijn van de uitgerekte delen van deze rechthoek, dan wanneer ze alle evenals het onderste bij AB samengedrukt zouden liggen. En de verhouding van de ruimte AEGLB tot de hele rechthoek ABCD, zal dezelfde zijn als die van de hoogte van de uitgerekte delen van rechthoek ABLN tot de hoogte van alle van rechthoek ABCD, zo samengedrukt als de onderste is; dat wil zeggen tot de hoogte 33000 voet.   Hier is dus ten eerste op te merken: aangezien een ruimte zoals AEGLB beslaat, groter en groter wordt genomen tot in het oneindige (want de ruimte tussen de hyperbool en de asymptoten is van oneindige grootte) volgt dat de hoogte van de lucht of van de atmosfeer oneindig is; tenminste als we aannemen dat het Boyleaanse experiment vaststaat bij welke uitrekking dan ook. Maar als lucht bestaat uit lichamelijke deeltjes die elkaar aanraken, want dit contact lijkt te worden aangetoond door die elastische kracht van lucht, kan het niet gebeuren dat enige luchtkolom zich uitstrekt tot in het oneindige, aangezien hij een bepaald gewicht heeft en een bepaalde hoeveelheid deeltjes. Het is dus eerder te geloven dat na een enorme uitrekking van lucht, niet langer die verhouding wordt aangehouden die het Experiment van Boyle laat zien. Maar toch, omdat voorzover de ondervinding strekt altijd is gevonden dat de uitkomsten uitstekend hebben beantwoord aan de verwachting, meen ik dat ze volstrekt niet zullen afwijken als we voortaan hetzelfde principe gebruiken om het volgende te berekenen. Want ook al zal misschien van de hoeveelheid lucht het honderdduizendste deel dat in de bovenste regio gelegen is, niet volgens die verhouding uitrekken, dit neemt niet weg dat deze voldoende nauwkeurig wordt aangehouden in alle overige lucht. Dus op grond van de bovengenoemde hypothese, alsof het experiment van Boyle overal zeker is, zullen we de volgende Problemen oplossen. [Marge:]     Probleem 1. Zoals wanneer ik wil weten tot welke hoogte we moeten stijgen om slechts een tiende deel van de lucht, dat wil zeggen volgens hoeveelheid of gewicht, boven het hoofd te hebben. Op deze plaats zal natuurlijk het kwik in de Torricelliaanse buis slechts 3 duim hoog blijven staan.   En ook andersom, als onderzocht moet worden, bij gegeven hoogte van een plaats boven het aardoppervlak, een hoe groot gedeelte, of hoeveel zwaarte, van de lucht overblijft boven en beneden, en evenzo tot welke hoogte het kwik in de buis opgehangen zal blijven 2). Eerst moet dus gevonden worden:   2)  Na de oplossing van dit laatste probleem te hebben genoemd in een brief van 17 aug. 1662 aan zijn broer Lodewijk, deelde Huygens de volgende dag de regels mee voor het oplossen van beide problemen; zie T. IV, p. 198, 202 en 205-206.

[ 486 ]

Bij een gegeven gedeelte of zwaarte van de lucht vanaf een plaats naar boven, te vinden hoe groot de hoogte van deze plaats is.   Laat een tiende deel van de lucht erboven zijn. Dus laat gesteld worden dat LC = 1/10 BC. Hieruit volgt, als LG evenwijdig is getrokken met de asymptoot CD, dat ook zal gelden LN of AB = 1/10 LG 1). Nu moet dus met de gegeven verhouding van GL tot AB gevonden worden de grootte van het oppervlak [spatij] ABLG, eerst in delen zoals waarvan het karakteristieke vierkant van de hyperbool of de rechthoek ABCD er 100000 heeft. En dit met de Regel die eerder is beschreven 2).

[ 4,88073 is de log. van de gezochte hoogte in voet die zal zijn 75986 voet.]

Maar omdat duidelijk is dat bij de logaritme 5,00000 opgeteld moet worden het constante getal 0,36222, en anderzijds van de som 5,36222 afgetrokken moet worden 0,48149 dat ook zelf hier steeds gelijk blijft, zal ter wille van de kortheid het constante getal bij deze regel 0,11927 kunnen zijn, dat namelijk het verschil is van die twee 0,48149 en 0,36222. Zodat de bewerking slechts op deze manier wordt uitgevoerd:   1)  Aangezien geldt AB : LG = LC : BC; vergelijk de eerste alinea van p. 485.   2)  Men vindt deze regel op p. 476  ["Bij gegeven getalverhouding van de lijnen die het segment begrenzen: neem het verschil van de logaritmen van elk getal, zoek de logaritme van dit verschil, tel er bij op 0,36221.., dan komt de logaritme van het gezochte oppervlak"]. Het gaat om de verhouding van de gezochte oppervlakte (hier ABLG) tot de rechthoek (AC) op de abscis en ordinaat van een punt van de hyperbool [de rechthoek is steeds gelijk aan het 'karakteristieke vierkant']. Hier dus: log opp. ABLG = log (log 10 – log 1) + log 100000 + const. [numerus perpetuus].   Zie noot 2 van p. 476.   3)  Toegevoegd wordt [bij log 1 = 0]:   log ABCD = log 100000 = 5 ;  zie p. 476, noot 1.

[ 487 ]

[ 4,88073 is de log. van de gezochte hoogte in voet die zal zijn 75986 voet.]

Laat boven een deel van de lucht zijn dat zich verhoudt tot het gewicht van de hele hoogte als 36789 tot 100000. Dat deel wordt NLCD gesteld. Aangezien dus BC tot CL is als 100000 tot 36789, zal dit ook de verhouding van GL tot AB zijn.

[ 4,51851 is de log. van 33000, de gezochte hoogte in voet.]

Wanneer we dus op die hoogte zijn, waar de atmosfeer zou eindigen als de lucht overal samengedrukt zou zijn zoals die waarin we hier leven, dan hebben we nog iets meer dan een derde deel van de lucht boven het hoofd. Maar dit derde deel kan tot een enorme hoogte verder worden uitgerekt. Het kwik in de buis zal hier 11 duim beslaan; omdat zoals 100000 tot 36789 is, zo is 30 duim tot 11.   Gegeven de hoogte van een plaats boven een vlak aardoppervlak, te vinden hoeveel zwaarte of welk deel van de lucht daar van bovenaf op drukt, en tot welke hoogte bijgevolg het kwik in de Torricelliaanse buis blijft staan.   Laat de gegeven hoogte 100000 voet zijn. De regel is dus de omgekeerde van de voorgaande.

3)  Toegevoegd wordt [bij log 1 = 0]:   log ABCD = log 100000 = 5 ;  zie p. 476, noot 1.   4)  Van het voorgaande getal wordt afgehaald log ABCD = 5 [hier blijft over: 0,11927 = log 1,3160].

[ 488 ]

Dus de verhouding van de hele lucht tot het gedeelte dat van boven drukt is die van 100000 tot 4831, dat is ongeveer van 21 tot 1. 100000 tot 4831 is als 30 duim tot 1 45/100 duim, wat de hoogte is van het kwik in de buis.   Laat de gegeven hoogte zijn 33000 voet.   Dus de hele lucht tot de er nog boven liggende lucht is als 100000 tot 36789.   Laat de gegeven hoogte zijn 380010 voet.   Hier is dus de hele lucht tot de er nog boven liggende als 100000 tot 1.   Laat de gegeven hoogte zijn 100,00000 [10 miljoen] voet.

[ 489 ]

Hier is de hele lucht tot de er nog boven liggende als 100000 tot 1 / (40739 122 zero). Ik heb gezegd 122 zero, want omdat de wijzer van de logaritme 126 is, moet het getal ervan bestaan uit 127 tekens, waarvan de 5 eerste zijn 40739. Doch het zou beter zijn bij zulke hoogten logaritmen met 10 tekens te gebruiken.   Wetenswaardig is dat als de hoogte gevonden is van de plaats waar nog 1/10 van de lucht boven is, zoals in het eerste voorbeeld van het vorige Probleem 1), ook gemakkelijk gevonden kunnen worden de hoogten waarboven ligt 1/100 of 1/1000 of 1/10000 enzovoorts. Immers de daar gevonden hoogte van 75986 voet, tweemaal genomen, zal overeenkomen met de verhouding 1/100 of van 100 tot 1, en driemaal genomen zal ze overeenkomen met de verhouding 1/1000 enzovoorts. En dit vindt plaats bij elke verhoudingsreeks 2).   Laat het gegeven deel van de lucht boven ons de helft zijn van de hele lucht.

[ 22873 voet is de gezochte hoogte ... 91492 voet waar 1/16 van de lucht boven ligt, enz.]

1)  Zie p. 486 en 487.   2)  Dit is een rechtstreeks gevolg van de regel, aangezien b.v. bij de verhouding 1/1000 in de berekening van het 1e voorbeeld (p. 487) het 1e en 3e van de 6 getallen vervangen moet worden door 3,00000 en het 4e door 5 + log 3 (zie noot 3 van p. 486), zodat het 6e getal wordt vermeerderd met log 3 en de hoogte dus verdrievoudigd wordt.

[ 490 ]

Laat de gegeven hoogte 100 voet zijn.   Dus op een toren van 100 voet hoogte zal het kwik in de buis van Torricelli 1/10 inch van de Londense voet dalen.   1)  0,00132 is het getal dat overeenkomt met de logaritme 2,11927 – 5 ; vergelijk noot 4 van p. 487.   2)  De hoeveelheid lucht boven de toren is dus tot de totale hoeveelheid als 99697 tot 100000, dus het kwik staat op 99697/100000 van de gewone hoogte van 30 duim.

[ 491 ]

Aanhangsel I  1) [1668?]  Over de hoogte van de Atmosfeer en de druk van de lucht.   Met de Boyleaanse experimenten is bevonden dat de ruimten die door eenzelfde hoeveelheid lucht in beslag worden genomen, in eenzelfde buis of in twee gelijke buizen, de omgekeerde verhouding aanhouden van de gewichten waarmee erop gedrukt wordt 2). En door het Torricelliaanse experiment staat vast dat de bovenlucht op deze onderste lucht drukt met evenveel gewicht als dat van een hoogte van 30 inch kwikzilver. Nu is de verhouding van de zwaarte van kwikzilver tot water 13 4/7 tot 1; en die van water tot lucht is door mij gevonden als 960 tot 1 3). Tot lucht natuurlijk zoals deze hier rondom ons is samengedrukt. Hieruit volgt dat een hoogte van 32640 voet van zo samengedrukte lucht zou opwegen tegen 30 inch kwikzilver. Doch laat ons het ronde getal van 33000 voet nemen. Hiermee hebben we het volgende gevonden.   Te bepalen tot welke hoogte we moeten gaan opdat een gegeven deel van de lucht boven ons hoofd is.   Laat het deel van de lucht een tiende zijn 4).   1)  Zie de tweede alinea van noot 1 van p. 483.       2)  Vergelijk noot 1 van p. 484.   3)  Zie voor deze gegevens de noten 2-4 van p. 483.   4)  Wat volgt in het Manuscript verschilt niet aanzienlijk van de tekst van stuk IV vanaf de berekening bovenaan p. 486 tot de woorden "waarvan de 5 eerste zijn 40739" (p. 489), behalve dat er niet het voorbeeld in staat waar de gegeven hoogte 33000 voet is. Dit gedeelte van de tekst is hier weggelaten. Dan laat Huygens daarna nog een berekening volgen zoals de laatste van p. 490, maar met een toren van 150 voet hoog; deze berekening is eveneens weggelaten.

[ 492 ]

Daar de Londense voet zich verhoudt tot de Parijse voet als 100 tot 109 1), en de hoogte van het kwik in de buis 30 inch van de Londense voet is, zal deze 27½ 2) twaalfde delen van de Parijse voet zijn.   Voor het constante getal vind ik bij deze berekening 15670 3), als we Parijse voeten willen gebruiken.   De heer Perier 4) heeft in de bergen van Auvergne ondervonden dat de hoogte van het kwik in de buis bij de voet van de berg 26 35/100 duim 5) van de Parijse voet was. En nadat ze ongeveer 3000 voet (want hij erkent dat de meting niet nauwkeurig genoeg is gedaan) omhoog gegaan waren, was de hoogte van het kwik 23 20/100 duim 6). Wat aan een onderzoek is te onderwerpen.   Aangezien aan de voet van de berg de hoogte van het kwik 26 35/100 duim was, wat in de onderste lucht moest zijn 27 50/100 duim 7), blijkt hieruit dat er beneden bij voet van de berg enige hoogte was, die we eerst hebben gevonden. Het gewicht namelijk van de lucht boven de top was tot het gewicht van de gehele lucht als 26,35 tot 27,50. Daarom moet een bewerking worden uitgevoerd volgens de vorige regel, op deze manier.

[ 1308 voet hoogte aan de voet van de berg.]

1)  In 1668 was deze verhouding nog niet goed bekend. Pas in 1675 was Huygens hierover beter ingelicht. Het is 100 tot 106,5783; zie p. 462 van T. VII.   2)  28 met de nieuwe verhouding.     3)  Met de gecorrigeerde verhouding: 14694.   4)  Zie OEuvres de Blaise Pascal (hier aangehaald op p. 196, n. 4), T. II, p. 351-358: 'Lettre de monsieur Perier à monsieur Pascal le jeune, du 22 septembre 1648', gepubliceerd in 1648 en in 1663 (zie ons T. VII, p. 252, n. 3). Vergelijk noot 1 van p. 365 van T. II van de OEuvres de Blaise Pascal.   5)  Beter 26 35/120, want er staat "26 poulces trois lignes et demie" [1648, p. 11] en bij Perier is de duim 12 lijnen, zoals blijkt uit zijn brief.   6)  Lees: 23 20/120.     7)  Lees: 27 50/120.     8)  Lees: 1293.

[ 493 ]

Op de hoogte volgens de schatting van de waarnemer van 3000 voet, was het gedeelte van de lucht boven de top tot het gewicht van de hele lucht als 23,20 tot 27,50. Dus is de ware hoogte boven het vlakke aardoppervlak. En als ervan wordt afgetrokken de boven gevonden 1308 voet 8), die de hoogte van de voet van de berg aanduiden, is er van deze 5148 9) nog 3840 voet over, en dit was de hoogte vanaf de voet van de berg tot de plaats van waarneming, die hij schatte op 3000 voet.   Op een hoogte van 162 voet (27 toises) was de stand van het kwik voor dezelfde waarnemer op dezelfde plaats 26 10/100 duim 10).

en dit was 162 voet; als het verschil zo groot is moet hetzij de kwikhoogte niet goed genoeg opgetekend zijn geweest, hetzij iets anders een rol hebben gespeeld 12). Dat het kwik zelf niet goed van lucht gezuiverd is,   9)  Met de genoemde correcties geeft de regel dat de Puy de Dôme beneden 1949 voet hoog is en boven 5867 voet. De top is in werkelijkheid 1465 m hoog, d.w.z. 4510 Parijse voet. Zie ook noot 1 van p. 494.   10)  Lees: 26 10/120.     11)  De regel geeft na correctie: 2196 – 1949 = 247.   12)  O.a. een lagere temperatuur van de lucht bij grotere hoogte. Hierdoor is de vermindering van de druk met de hoogte sterker: de regel van Huygens overdrijft de hoogteverschillen.

[ 494 ]

waardoor in het lege deel van de buis enige lucht zou zitten, kan niet gezegd worden, omdat als dit zo was hierdoor noodzakelijk een kleiner hoogteverschil van het kwik was opgetreden.   Of er moet een andere verhouding zijn van de zwaarte van lucht tot kwik en water dan die van ons van 1 tot 960 1).   Het constante getal in de laatste gevallen wordt gevonden door 0,36222, de constante voor de eerder gevonden 2) afmeting van de hyperbool, af te trekken van het verschil tussen de logaritme van 100000 en de logaritme van het aantal voet van de hoogte van de luchtkolom die opweegt tegen de kwikkolom in het experiment van Torricelli 3).   1)  Bij 10° C is het ongeveer 1 : 801. Voor correctie moeten de hoogten dus nog verkleind worden in de verhouding 960 : 801. Dan wordt de hoogte van de Puy de Dôme 4895 Parijse voet volgens de gecorrigeerde formule.   2)  Zie p. 476.     3)  Vergelijk p. 486 en 492.