T H E O R E M   V I 1 1.   Weight on EF =   gravity of water GHFE.       On any bottom of the water being parallel to the horizon there rests a weight equal to the gravity of the water the volume of which is equal to that of the prism whose base is that bottom and whose height is the vertical from the plane through the water's upper surface to the base. *) Stevin's words. [ *)  Translation from Principal Works, vol. I, p. 415; Introd. p. 377.] Master Simon | Water pressure 1 | Next   Supposition. Let ABCD be a water, whose form be a corporeal rectangle, whose upper surface be AB and a bottom therein EF, parallel to the horizon. Let also GE be the vertical from the plane through the water's upper surface to the bottom EF, and the prism comprehended by the bottom EF and the height EG shall be GHFE.   What is required to prove. We have to prove that on the bottom EF there rests a weight equal to the gravity of the water of the prism GHFE. Stevin's words. Back | Water pressure 2 | Next   Proof. If there rests on the bottom EF more weight than that of the water GHFE, this will have to be due to the water beside it. Let this, if it were possible, be due to the water AGED and HBCF. But this being assumed, there will also rest on the bottom DE, owing to the water GHFE, because the reason is the same, more weight than that of the water AGED; and on the bottom FC also more weight than that of the water HBCF; and consequently on the entire bottom DC there will rest more weight than that of the whole water ABCD, which (in view of ABCD being a corporeal rectangle) would be absurd. In the same way it can also be shown that on the bottom EF there does not rest less than the water GHFE. Therefore, on it there necessarily rests a weight equal to the gravity of the water of the prism GHFE. Stevin's words. Back | Water pressure 3 | Next Corollary I. 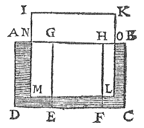Weight of IKLM = weight of water column NOLM (Archimedes' principle).   Let us now lay in the water ABCD of the 10th proposition a solid body IKLM, of greater specific levity than water, i.e. floating on the water, with the part NOLM within the water and with the part NOKI above it. This being so, the solid body IKLM is of equal weight to the water having the same volume as NOLM, by the 5th proposition, owing to which the body IKLM, with the remainder of the water surrounding it, is of equal weight to a body of water having the same volume as ABCD. Therefore we still say, according to the proposition: against the bottom EF there rests a weight equal to the gravity of the water having the same volume as the prism whose base is EF and whose height is the vertical GE, from the plane AB through the water's upper surface AN to the base EF. From which it appears that if any floating substance is laid in the water, it does not weight or lighten the bottom (provided the water remain at the same level). Stevin's words. Back | Water pressure 4 | Next Corollary II. Let there again be put in the water ABCD a solid body, or several solid bodies of equal specific gravity to the water. I take this to be done in such a way that the only water left is that enclosed by IKFELM.

This being so, these bodies do not weight or lighten the base EF any more than the water first did. Therefore we still say, according to the proposition: against the bottom EF there rests a weight equal to the gravity of the water having the same volume as the prism whose base is EF and whose height is the vertical GE, from the plane AB through the water's upper surface MI to the base EF. Stevin's words. Back | Water pressure 5 | Next Corollary III. Let again ABCD be a water, and EF a bottom therein, parallel to the horizon. This being so, the water below the bottom EF exerts an upward thrust against it as great as the downward thrust which the water above the bottom EF exerts against it. For if this were not so, the weakest would give way to the strongest, which does not happen, for each keeps its appointed place, by the 1st proposition. Now let a number of solid bodies of equal specific gravity to the water be laid therein in such a way that the water IKEFLM thrusts against EF from below. 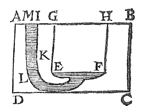This being so, the water below the bottom EF exerts the same thrust against EF, i.e. against the solid body, as it did before against the water. But it exerted against the latter the same thrust as the upper part against EF, as has been said above, and the upper part exerted a thrust against EF according to the present proposition. Therefore the lower part also exerts a thrust against EF according to the present proposition, that is, as we have said above: against the bottom EF there still rests a weight equal to the gravity of the water having the same volume as the prism whose base is EF and whose height is the vertical GE, from the plane AB through the water's upper surface MI to the base EF. Stevin's words. Back | Water pressure 6 | Next Corollary IV. Let us now put the solid bodies of the 2nd and the 3rd corollary in their places, and pour out the water. Then there will be left an empty space IKEFLM, and the base EF will not bear any weight; from which it is apparent that by pouring that small empty space full of water again, the base EF will be weighted as much as if the whole vessel ABCD (the solid bodies laid therein being taken away) were full of water. Stevin's words. Back | Water pressure 7 | Next Corollary V. But since the solid bodies of the 2nd and the 3rd corollaries are put in their places, their outward matter neither adds to nor subtracts from the weighting or lightening of the base EP. Therefore let us cut away the matter thereof all round, in such a way that the interior irrregular forms or vessels filled with water, MIKFEL, are left, as shown below.