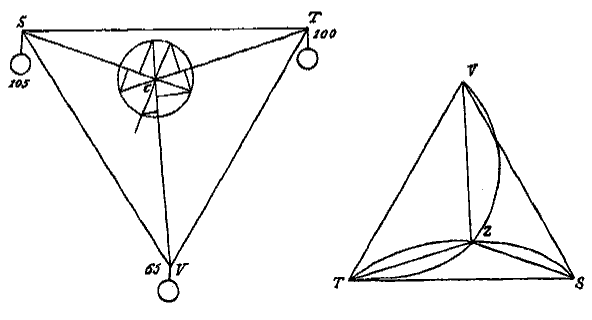
Δ STV is gelijkzijdig. In de hoeken van STV hangen via katrollen ongelijke gegeven gewichten, verbonden door draden die samenkomen in C. Gevraagd wordt hoe het punt C te vinden is waar de knoop zal stilstaan.     Antwoord. Maak Δ PQR waarvan de zijden een zelfde onderlinge verhouding hebben als de gegeven gewichten. Van de hoeken van deze Δ zijn de complementen tot twee rechte hoeken [dus: supplementen] die hoeken, die ontstaan bij knoop C. Zodanig dat het kleinste complement omvat wordt door de draden die vastzitten aan de twee kleinste gewichten; en het grootste complement omvat wordt door de draden die vastzitten aan de twee grootste gewichten. Dus als op twee zijden van driehoek STV bogen beschreven worden die de genoemde complementen bevatten, zal hun snijpunt het gevraagde punt Z tonen.

[ 395 ]

Het is evenwel nodig dat geen enkele hoek van Δ PQR groter is dan 120 graden, dat wil zeggen dat het kwadraat van het grootste gewicht niet groter is dan de kwadraten van de twee kleinste samen met hun product, anders zou namelijk het snijpunt niet binnen Δ STV vallen als deze immers gelijkzijdig gegeven wordt. No 612. Uittreksel uit de Adversaria van Christiaan Huygens. 14 maart 1659. Aanhangsel II bij No. 610. 14 Maart 1659. Mijn probleem, voor te leggen aan Dirk Rembrantz. [>]     A en B zijn katrollen, ACBDA is een doorgaand touw; AC = CB, AD = DB. Gegeven is de opgehangen zwaarte in C en D; eveneens gegeven is AB, en de lengte van touw ACBDA. Te vinden in welke stand de zo opgehangen gewichten in rust zijn.     Neem op CL een punt S en trek SB. Deze is te beschouwen als evenwijdig met BC, omdat CS iets heel kleins is. Neem aan dat SQ loodrecht staat op BC. Als dus C omhoog zou gaan naar S, zou daardoor BS zoveel kleiner worden dan BC als QC. Maar tegelijk daalt D naar O; en deze afstand DO wordt gevonden als volgt. Getrokken wordt OB; deze is als evenwijdig met BD te zien; en daarop valt DP loodrecht. Bijgevolg zal PO gelijk zijn aan QC, omdat, daar BS kleiner is dan BC met het stukje CQ, het noodzakelijk is dat BO evenveel langer wordt dan BD.

[ 396 ]

Omdat nu de driehoeken CQS en OPD rechthoekig zijn, met onderling gelijke bases CQ en OP, zal dientengevolge CS zich tot OD verhouden als de secans van hoek SCQ of LCB tot de secans van hoek DOP of LDB. En indien de gewichten in deze stand zullen blijven, moet de daling DO tot de stijging CS dezelfde verhouding hebben als het gewicht dat aan C hangt tot het gewicht aan D.     Laat hoek LCF gelijk zijn aan hoek LDB, doordat namelijk CF getrokken is evenwijdig aan DB. Als dan CL als eenheid wordt genomen, wordt CF de secans van hoek LDB, en CB de secans van hoek LCB. Daarom moet BC tot CF staan als het gewicht aan D tot het gewicht aan C. Een dergelijke stand te vinden is evenwel een stevig probleem. Maar als bijvoorbeeld gegeven is: LC = 1, CB = 4, LD = 7, is duidelijk dat de zwaarten D en C te vinden zijn. Aangezien namelijk zwaarte D tot zwaarte C is als CB tot CF, en de verhouding CB tot CF wordt samengesteld uit CB tot BD, en BD tot CF, of DL tot LC, daarom zal zwaarte D tot zwaarte C zijn als het product van CB en DL, tot dat van BD en CL.     Hier wordt BD = 8. Dus het product van CB en DL zal 28 zijn, en het product van BD en CL is 8. Dit is als 7 tot 2. Dus is ook zwaarte D tot zwaarte C als 7 tot 2.     [ Zie ook XVI, 379-380: vertikale driehoek, katrol met twee gewichten.]