[ Twee problemen van 1659 over het evenwicht van verschillende gewichten opgehangen aan draden. Het zijn No. 611 en 612 (p. 394 en 395) van Tome II.] II 2). [Oct. 1659] 3)

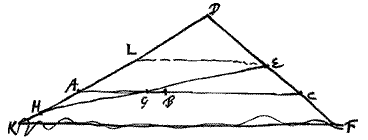
1.   AH EC 4), HE en AC zijn lijnen 5). Aangetoond moet worden dat  6). Laat EL evenwijdig zijn met CA.

[ 380 ]

Dus zoals AD tot DC zo is LD tot DE, en AL tot EC, of AL tot AH, want AH EC.   Maar zoals LA tot AH zo is EG tot GH. Dus EG tot GH als AD tot DC. Wat te bewijzen was.   2.   Het omgekeerde is ook waar; immers als binnen de hoek ADE getrokken worden de twee HE en AC, en als geldt: zoals AD tot DC zo EG tot GH, dan zullen ook HA en EC gelijk zijn.   Want omdat zoals AD tot DC zo AL tot CE, zal dus AL tot CE zijn als EG tot GH, dat is als LA tot AH. En daarom is EC gelijk aan AH.

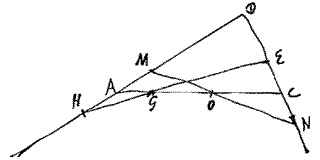
3.   Laat weer AC en HE elkaar snijden in G, en zoals AD tot DC zo EG tot GH. En neem HM gelijk aan EN; en verbind M met N. Ik zeg dat deze gesneden wordt door de rechte AC in O, zodanig dat NO tot OM is zoals EG tot GH of als AD tot DC.   Immers AH EC volgens 2. Dus door deze af te trekken van de gelijke HM en EN blijven over de gelijke AM en CN. Dus geldt volgens 1: zoals AD tot DC zo NO tot OM, of als EG tot GH. wat aangetoond moest worden.

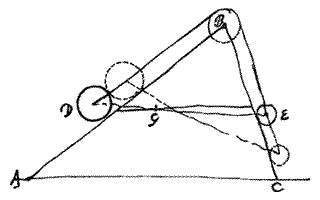
[4.]   Als er een driehoek ABC is waarvan de zijde AC evenwijdig is met de horizon, en als op de zijden ervan gewichten hangen, met een touw verbonden, D en E, waarvan de zwaarte van D tot E is als zijde AB tot BC; dan zullen de gewichten elke gegeven stand handhaven.   Omdat het gemeenschappelijk middelpunt van hun zwaarte G niet daalt ook al beginnen de gewichten te bewegen, maar steeds op dezelfde hoogte blijft, zoals uit het voorgaande gemakkelijk wordt aangetoond.*)   1)  Manuscript A, p. 90 [HUG 10, 45v] en 92 [HUG 10, 46v]. Zie ook de briefwisseling van Huygens en D. Rembrandtz. van Nierop in 1659 [<].   2)  Manuscript A, p. 156 [HUG 10, 78v]. § 1, 2 en 3 zijn zuiver meetkundig, maar § 4 (die volgt op § 3) behandelt een geval van statica.   3)  P. 155 [HUG 10, 78r] heeft de datum 11 oct. 1659 en p. 157 [HUG 10, 79r] is gedateerd: oct. 1659.   4)  Het teken geeft gelijkheid aan. Vergelijk noot 3 van p. 7 van T. XI [Huygens is dit teken steeds blijven gebruiken, maar het wordt wel eens vervangen door '=', het moderne gelijkheidsteken].   5)  D.w.z. rechte lijnen.   6)  D.w.z. EG : GH = AD : DC. Vergelijk noot 19 van p. 13 van T. XI.   [ *)  Simon Stevin wordt hier niet genoemd, maar wel in 1676, waarbij in de biografie (p. 699) de vraag wordt gesteld of Huygens dit bewijs toen vergeten was.]