Home | Chr. Huygens | Oeuvres XXI | Astronomica varia

Astronomica varia

1690-1691

[ 571 ]
I.  Snelheden van de materie van veelzijdige wervels. 1)

  Als de juiste snelheden van de fluïde materie omgekeerd evenredig zijn met de tweede machten van de afstanden tot het middelpunt, dan zullen de zwaartes omgekeerd evenredig zijn met de kwadraten van de afstanden, zoals meneer Newton vaststelt, en hij bewijst het met het evenwicht van de Planeten 2).

3 cirkels, lijnen
HUG 7
 
Want een planeet die negen keer zo ver weg is als een andere gaat drie keer zo langzaam met zijn eigen beweging in zijn baan 3), zoals is af te leiden uit de periodieke tijden, die van 27 tot 1 zijn, waaruit men de centrifugale kracht ervan vindt als 1/81 van de centrifugale kracht van meest nabije.
Om dus zijn zwaarte eveneens 1/81 van de zwaarte van de meest nabije te maken, moet de centrifugale kracht van de fluïde materie op de plaats van de verste ook 1/81 zijn van de centrifugale kracht van de fluïde materie op de plaats van de meest nabije. Wat ook zo zal zijn als de snelheid van van deze materie dichtbij de verre planeet 1/3 is van de snelheid ervan dichtbij de meest nabije.
Zodat de snelheden van de materie op de plaats van elke planeet dezelfde verhouding behouden als de snelheden van de planeten zelf.


  Dit is van toepassing op een geheel van veelzijdige wervels: we weten (zie ons Voorbericht [p. 429] bij Discours de la Cause de la Pesanteur) dat Huygens sinds de verschijning van de Principia van Newton deze wervels aannam voor het zonnestelsel.

  1)  Manuscript G, p.52v [HUG 7]. p. 53r heeft de datum 27 aug. 1690.
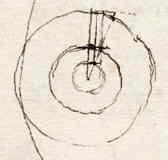
[ Figuur naast tekst, er omheen een kring, waarvan links in de figuur een deel te zien is (geen komeet). Er onder: "Response à l'objection de M. Papin", zie brief No. 2617 in T. 9, p. 483.]
  2)  Wat Newton 'vaststelt' is naar men weet alleen dat de 'zwaartes', om 'evenwicht van de Planeten' te geven, omgekeerd evenredig moeten zijn met de kwadraten van de afstanden.
[ Newton over 'subtiele materie', Principia, transl. A. Motte (N.Y. 1846), p. 321:]
... since it is the opinion of some that there is a certian aethereal medium extremely rare and subtile, which freely pervades the pores of all bodies; and from such a medium, so pervading the pores of bodies, some resistance must needs arise ...
[ Dan volgt een proef met een slinger om na te gaan of een doos vol lood meer weerstand ondervindt dan een lege doos. Uitkomst: de verhouding is niet groter dan 78 : 77.]
  3)  Alle banen zijn volgens de hypothese cirkelvormig en concentrisch.



[ 572 ]
II.  Mercurius op de Zon waargenomen te Neurenberg
31 okt. 1690.

  ...



[ 573 ]
III.  Firmamentum Sobiescianum.
Uit 'Prodromus' van Hevelius.

  ...



[ 576 ]
IV.  Conjunctie van Venus en de Zon.
15 nov. 1681 te Parijs.

  ...



[ 577 ]
V.  Bestaan de wervels echt? 1)

  Verscheidenen nemen de wervels van Descartes aan; zoveel meer houdt men ervan zich in te beelden te weten, dan onwetend te blijven zonder aan iets vast te houden.


  Hoewel het hier niet gaat over de veelzijdige wervels van Descartes (zie stuk I hiervoor) lijkt deze zin van Huygens wel een meer algemene betekenis te hebben.

  In de 'Cosmotheoros' zullen de (veelzijdige) wervels pas aan het eind hun intrede doen: Huygens handhaaft het bestaan ervan, maar hij geeft er niet meer een ereplaats aan. Het is mogelijk dat hij in dit stuk slechts bedoelt te spreken over gewone mensen.
Toch lijkt het eveneens mogelijk dat het ook natuurkundigen en astronomen zijn. In dat geval zou men hem hier — voor een ogenblik en geheel voor zichzelf — zien als voorstander voor een natuurkunde die ongetwijfeld hypotheses opstelt maar zonder aan iets vast te houden; wat ons herinnert aan het beroemde 'ik verzin geen hypotheses' van Newton 2).

  Vergelijk over de twijfel van Huygens Aanhngsel I (noot 3) bij de 'Cosmotheoros'.


  Vergelijk ook met dit stuk de titel, aangehaald op p. 563, n.1, van een van de dialogen van de La Mothe Le Vayer: De l'ignorance louable (Over prijzenswaardige onwetendheid).


  1)  Chartae astronomicae, f. 127 [HUG 28, 127bis v]. Enkele opmerkingen ontleend aan dit blad staan op p. 536 en 568. zie ook p. 315 [Lat. gedichtje van Huygens ter ere van zichzelf, datum onbekend; vergelijk p. 519, § 13].
  2)  Vergelijk het citaat van Newton in noot 13 van p. 5 van T. 19.



Home | Christiaan Huygens | XXI | Astronomica varia, 1690-1691 (top)