D. Papin aan Christiaan Huygens.
18 juni 1690.Brief in Leiden, collectie Huygens.
Gepubliceerd door E. Gerland 1).
Antwoord op een onbekende brief 2). Chr. Huygens; antwoord: No. 2617. a)
de Marbourg ce 18/8 Juin 1690.
 Ik kan U niet de aangename verrassing te kennen geven, veroorzaakt door de eer die U mij hebt willen doen door me het laatste werk te sturen dat U aan het licht hebt gebracht, en ik zou U mijn zeer ootmoedige dank eerder hebben doen toekomen, als het niet zo lang onderweg was geweest.
Ik kan U niet de aangename verrassing te kennen geven, veroorzaakt door de eer die U mij hebt willen doen door me het laatste werk te sturen dat U aan het licht hebt gebracht, en ik zou U mijn zeer ootmoedige dank eerder hebben doen toekomen, als het niet zo lang onderweg was geweest.
Maar door deze vertraging heb ik het nog slechts inderhaast kunnen doornemen, en dit moest op zijn minst gedaan worden alvorens U ervoor te bedanken, om U tegelijk te betuigen dat ik al een deel heb erkend van wat dit mooie geschenk waard is, en dat ik ervoor zal zorgen mijn voordeel ermee te doen. Want ik weet. Meneer, dat dit het doel is van uw werken, en dat U, in het bezit van iets dat U gelukkig en tevreden maakt, daarna alles in het werk stelt het goede aan anderen te verschaffen.
Ik zal U dus zeggen dat, hoewel ik niet in staat ben zo vlug te oordelen over het meeste van de stoffen die in uw boek zijn omvat, daar er zeer diepe onderzoekingen en Bewijsvoeringen zijn, die een zeer moeilijke aansluiting vragen van degenen die zoals ik slechts hebben gewerkt aan onderwerpen die veel makkelijker zijn; toch vertrouw ik genoeg op uw doorknede bekwaamheid in dit soort dingen, om ervan overtuigd te zijn dat alle berekeningen en Bewijsvoeringen die U in dit boek geeft, precies bewijzen wat u beweert en dat, als de Experimenten blijken overeen te stemmen met wat uw Theorie belooft, dit een bijna onbetwijfelbaar bewijs is dat uw Hypothesen ook waarheden zijn, en ik ben er zeker van dat ze steeds meer bevestigd zullen worden door onderzoek dat men vroeger of later in navolging van u zal uitvoeren.
Het zou te wensen zijn, Meneer, dat er veel mensen zijn die de wil en het vermogen hebben om het te doen; dan zou men daadwerkelijk veel echte vorderingen maken in de kennis van de Natuur; maar U moet wel meer bewonderaars verwachten dan
1) Leibnizens und Huygens' Briefwechsel mit Papin, Berlin 1881, p. 148. Zie No. 2008, n.11.
2) Brief bij de verzending van Traité de la lumière en Discours sur la Cause de la Pesanteur [Ned. Het eerste is vertaald door Dieuwke Eringa, Verhandeling over het licht, Epsilon, 1990, met origineel.]
a) Beantwoord op 2 sept. 90 (Chr Huygens).

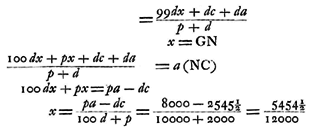 5)
5)

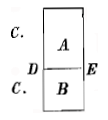 U zegt dat als men van lichaam AB de helft A naar C duwt, er geen reden is die zou doen geloven dat deel B dezelfde kant op zal gaan. En u beweert dat alleen de druk van omgevende vloeistoffen de vastheid en hardheid veroorzaakt die we vinden zoals ze zijn.
U zegt dat als men van lichaam AB de helft A naar C duwt, er geen reden is die zou doen geloven dat deel B dezelfde kant op zal gaan. En u beweert dat alleen de druk van omgevende vloeistoffen de vastheid en hardheid veroorzaakt die we vinden zoals ze zijn. 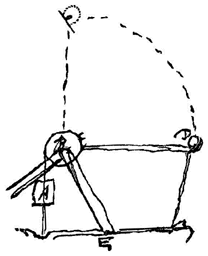 Maar door uw luchtledige buis ervoor te nemen, en niets te rekenen voor belemmeringen, zou hij gaan tot 8000 voet. Waaraan te zien is dat deze buis vooral een groot voordeel geeft wanneer het gewicht van de kogel klein is; maar als men stelt dat er 100 pond nodig is voor de wrijvingsweerstand van de zuiger en niets voor zijn gewicht of andere beletselen, zal de kogel kunnen gaan tot een hoogte van 7600 voet.
Maar door uw luchtledige buis ervoor te nemen, en niets te rekenen voor belemmeringen, zou hij gaan tot 8000 voet. Waaraan te zien is dat deze buis vooral een groot voordeel geeft wanneer het gewicht van de kogel klein is; maar als men stelt dat er 100 pond nodig is voor de wrijvingsweerstand van de zuiger en niets voor zijn gewicht of andere beletselen, zal de kogel kunnen gaan tot een hoogte van 7600 voet. 
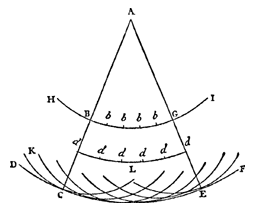
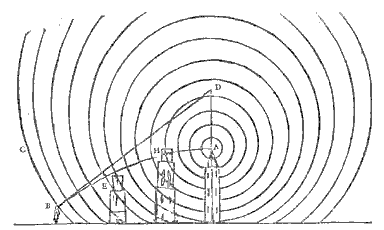
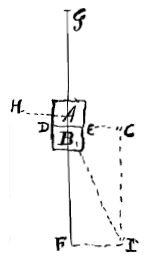 Om dit te bewijzen. Meneer, verzoek ik U te overwegen dat A en B niet in absolute rust zijn; maar dat ze voortdurend in dezelfde toestand zijn als wanneer ze met een bepaalde snelheid tegen elkaar zouden botsen. Want als men plotseling B zou wegnemen, bijvoorbeeld met de vloeistof die ertegen drukt van F naar G, zou deel A op hetzelfde ogenblik naar F gaan en er aankomen in de tijd 1" bijvoorbeeld, net zoals wanneer het in de voorgaande 1" van G naar A was gekomen; evenzo zeg ik dat B naar G zou gaan als men A zou wegnemen.
Om dit te bewijzen. Meneer, verzoek ik U te overwegen dat A en B niet in absolute rust zijn; maar dat ze voortdurend in dezelfde toestand zijn als wanneer ze met een bepaalde snelheid tegen elkaar zouden botsen. Want als men plotseling B zou wegnemen, bijvoorbeeld met de vloeistof die ertegen drukt van F naar G, zou deel A op hetzelfde ogenblik naar F gaan en er aankomen in de tijd 1" bijvoorbeeld, net zoals wanneer het in de voorgaande 1" van G naar A was gekomen; evenzo zeg ik dat B naar G zou gaan als men A zou wegnemen.