Nu twee gewichten aan een massieve balk:
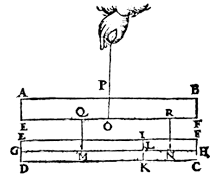
ABCD is langs EF doorgesneden, en het onderste stuk langs IK. Zwaartepunten zijn M en N.
Hang de twee stukken aan MQ en NR zo, dat
linkergewicht : rechter = OR : OQ
Er blijft evenwicht.

Conclusie:
Stelling 1 is bewezen voor elke stof en vorm.

  M E N  can tvoorgaende oock bethoonen, blyvende de twee swaerheden hanghende an eenen lichamelicken balck, in deser voughen: Laet den pilaer ABCD ghesneen sijn in twee deelen, met een plat door den as EF [...], ende het swaerheydts middelpunt van het deel IKDE sy M int middel van GL, ende van het deel IKCF sy N [...].
  L A E T  ons nu het onderste deel EFCD neertrecken, also dat het blyve hanghende ande linien MQ ende NR [...]. Laet ons nu achten dat het deel IKDE, ghesneen sy van IKCF, ende dat elck deel vallen mach daert wil [...].
Maer IKDE, sulcken reden te hebben tot IKCF, als den erm OR, tot den erm OQ, is vooren beprouft; Inder voughen dat tghene eerst betoocht was anden weegconstighen balck (dat is een lini) sulcx hebben wy hier verclaert an een lichamelicken.

  T B E S L V Y T. {Conclusio.}   Wesende dan twee evestaltwichtighe swaerheden, de swaerste heeft sulcken reden tot de lichtste (van wat stof ofte form oock de lichamen sijn) als den langsten erm tot den cortsten, twelck wy bewysen moesten.