Stevin | Master Simon | Carrying a load
S . S T E V I N S     W E E G H D A E T.


Proposition VIII.

  To examine the qualities of gravities that are being carried. *)

2 personen dragen een ladder op de schouder
Centre of gravity: F.
GE = HE.
 

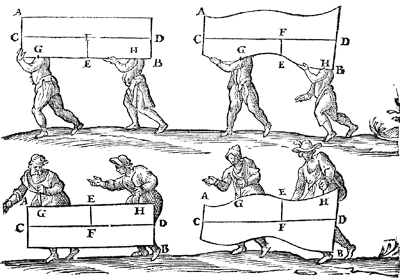
  Supposition.  Let AB be a ladder, heavier at one end than at the other end, as they usually are,

which is to be carried by two men in such a way that one shall carry as much weight as the other, i.e. each one half;

and its centre line CD shall remain parallel to the horizon during the carrying.

  Construction.  The ladder shall be laid on a sharp edge and pulled forwards and backwards until equality of apparent weight is found to he attained, which I take to be in E;
and if the ladder has to be often carried from one place to another, a notch may be made at E.

Thereafter let there be drawn the vertical EF, intersecting CD in F, and then two points shall be marked at equal distances from EF, as G and H;
then the man carrying the ladder at G will carry the same weight as the one at H.


Stevin's words.

[ *)  Translation from Principal Works, vol. I, p. 333.  Figures from DBNL, Wisc. Ghed. 4.]

Meester Simon | Load 1 | Next



  But if it be desired to have that one carry twice the weight of this one, the distance between the latter and EF shall be made double of that between the former and EF.

If HE were double of EI, the man carrying at I would carry twice the weight of the man [or woman] at H.

2 personen dragen een ladder, op de schouder, en aan de hand
GE = HE.       F: centre of gravity.       HE = 2 IE.

And thus the ratio of the weight of the one to that of the other can be fixed according to requirement.


Stevin's words.


Back | Load 2 | Next



  What has been said above of the ladder will also apply to any body whatever, as for example the figure shown below,
bearing in mind that with irregular bodies the lines passing through their centres of gravity, as CD, are found by means of the 1st proposition of the present book,
and also that the verticals through G and H are equidistant from the lines EF.

2 personen dragen een last, 4 manieren
F: centre of gravity.  G and H: same distance from EF.


Stevin's words.


Back | Load 3 | Next


  We have here given examples in which the line CD is taken parallel to the horizon, but if it were non-parallel thereto, and the men were ascending a mountain or height, the ratio of the weights would change, but remain known.

For the sake of greater clarity, let the aforesaid men ascend a height, as shown below, the man at G going in front and the other behind.

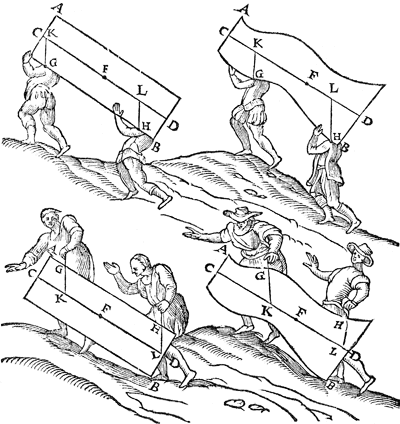
2 personen dragen een last bergop, 4 manieren


Stevin's words.


Back | Load 4 | Next


  The verticals through the points G, H now being drawn, which intersect CD in K and L, each of the men will not then carry as much as in the first figure, for FK in the two figures at the top is greater than FL, and in the figures at the bottom less.
And as FK is to FL, so is the weight of the man carrying at H to the weight of the man carrying at G.

2 personen dragen een last bergop, 4 manieren
FK : FL  =  weight at H  :  weight at G.

From which it also appears that if the fixed points G, H are below the line CD, the man in front carries least, but if these fixed points are above the line CD, the man in front carries most.

It is also evident that if the fixed points G, H are in the line CD, each of the men will then always carry the same weight everywhere, both when ascending a mountain and when walking parallel to the horizon, the proofs of all of which are manifest from the 14th, 15th, 16th, 17th, 18th, 27th, 28th propositions of the 1st book.

Stevin's words.

Back | Load 5 | Next



But because many workmen have no opportunity to learn these propositions or to exercise themselves therein, and yet would like to see some evidence of it from which they can believe it, let them take any straight, regular or crooked, irregular stick, as AB, suspending it in some place, as C, by a cord CD.
tak met gewichten
2 situations:
E and F,  E = F:  HL = LK.
M and F,  M = 2 F:  LK = 2 LN.
 

Thereafter, equal weights, as E and F, hanging at the stick in such a way that their cords GH, IK are equidistant from the line CD drawn downwards, to wit that HL shall be equal to LK, the stick will keep its first position.

It will do the same, if E be taken away and the weight M, double of F, be suspended in such a way that LK shall also be double of LN,

and thus with all the others, from which they will easily understand the necessity of what has been said above.


Stevin's words.


Back | Load 6 | Next


The lines by which the men in the preceding figures carry the body are placed at right angles to the horizon,

but if they are at oblique angles thereto, as in the figure, they will have to exert together a greater force than the gravity of the body itself.

But in order to know how much each of them is carrying, the verticals IM and NO shall be drawn, and it shall be said:

2 personen trekken schuin aan langwerpig gewicht
MI  :  IG  =  lifting weight  :  weight pulled, at G.
ON : NH  =  lifting weight  :  weight pulled, at H.

as MI is to IG, so is the vertical lifting weight along MI to the weight pulled by the man at G,
and again as ON is to NH, so is the vertical lifting weight along ON to the weight pulled by the man at H,
by the 27 proposition of the 1st book of the elements, and the force exerted by each becomes known from the 22nd proposition of the same book.


Stevin's words.




Back | Load 7 | Master Simon