Meester Simon: waterdruk

S. S T E V I N S B E G H I N S E L E N D E S W A T E R W I C H T S.

S T E L L I N G V I 1 1:

Op iedere horizontale waterbodem rust een gewicht, gelijk aan de zwaarte van een waterkolom met die bodem als basis, en de loodlijn van het wateroppervlak tot de bodem als hoogte.

Stevins woorden:

V I I I V E R T O O C H. X V O O R S T E L.
O P yder bodem des waters evewydich sijnde vanden sichteinder {Parallelum cum Horizonte.}, rust een ghewicht even ande swaerheyt waters die evegroot is met den pilaer, wiens grondt dien bodem is, ende hoochde, de hanghende lini van t'plat {Perpendicularis. Plano.} duer t'waters oppervlack tot den grondt.

Meester Simon | Waterdruk 1 | Volgende

Gegeven:

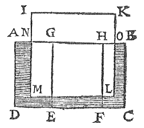
Laat ABCD water zijn in de vorm van een rechthoekig blok, waarvan het oppervlak AB is, en een bodem daarin EF, evenwijdig met de horizon.

Laat ook GH de loodlijn zijn van het vlak door het wateroppervlak tot de basis EF.

De kolom gevormd door de bodem EF en de hoogte EG is GHFE.

Gevraagd:

Wij moeten bewijzen dat op de bodem EF rust het gewicht, gelijk aan de zwaarte van de waterkolom GHFE.

Stevins woorden:

T' G H E G H E V E N. Laet ABCD een water sijn, van form een lichamelick rechthouck, diens oppervlack AB is, ende eenighen bodem daer in EF, evewydich vanden sichteinder; Laet oock GE de hanghende lini sijn van t'plat duer t'waters oppervlack totten grondt EF, ende den pilaer begrepen onder den bodem EF ende hoochde EG, sy GHFE.

T' B E G H E E R D E. Wy moeten bewysen dat opden bodem EF, rust het ghewicht even ande swaerheyt waters des pilaers GHFE.

Vorige | Waterdruk 2 | Volgende

Bewijs:

Als op de bodem EF meer gewicht rust dan dat van het water GHFE, zal dat moeten komen van het water ernaast.
Stel, als het mogelijk zou zijn, van het water AGED en HBCF.

Maar dan zal op de bodem DE vanwege het water GHFE, om dezelfde reden, ook meer gewicht rusten dan dat van het water AGED; en op de bodem FC ook meer dan van het water HBCF.

En dientengevolge zal er op de hele bodem DC meer gewicht rusten, dan dat van al het water ABCD, wat niet uitkomt (gezien het feit dat ABCD een rechthoekig blok is).

Evenzo kun je ook aantonen dat op de bodem EF niet minder rust dan het water GHFE.
Daarop rust dan noodzakelijk het gewicht, gelijk aan de zwaarte van de waterkolom GHFE.

Stevins woorden:

T' B E W Y S. Soo op den bodem EF meer ghewicht rust dan des waters GHFE, dat sal moeten commen van weghen t'nevenstaende water; Laetet sijn soot mueghlick waer, van t'water AGED ende HBCF;
Maer dat soo ghenomen, daer sal op den bodem DE, van weghen t'water GHFE, om dat de reden de selve is, oock meer ghewichts rusten dan des waters AGED; ende op den bodem FC, oock meer ghewichts dan des waters HBCF,
ende vervolghens op den heelen bodem DC sal meer ghewichts rusten, dan des heelen waters ABCD, t'welck (ghemerckt ABCD een lichamelick rechthouck is) ongheschickt waer.
S'ghelijcx salmen oock bethoonen dat opden bodem EF niet min en rust dan t'water GHFE, daer rust dan nootsakelick op t'ghewicht even ande swaerheyt waters des pilaers GHFE.

Vorige | Waterdruk 3 | Volgende

Gevolg 1

Laten we nu in dit water ABCD een voorwerp IKLM leggen, met een kleinere dichtheid dan water.

Dat drijft op het water, met het deel NOLM erbinnen, en het deel NOKI erbuiten, in een opstelling zoals hiernaast.

Zodat het voorwerp IKLM evenveel weegt als het water dat in NOLM past, volgens de wet van Archimedes.
Dus met het water er omheen: evenveel als het water dat in ABCD past.

Daarom kunnen we nog steeds zeggen, dat tegen de bodem EF een gewicht rust, gelijk aan de zwaarte van de waterkolom GHFE.

Waaruit blijkt dat een in het water gelegde drijvende stof de bodem niet verzwaart of verlicht (wel te verstaan als het water op dezelfde hoogte blijft).

Stevins woorden:

I V E R V O L G H.

Laet ons nu in t'water ABCD des 10^en voorstels, legghen een styflichaem IKLM, stoflichter dan water, dat is drivende op t'water, mettet deel NOLM daer binnen, ende mettet deel NOKI daer buyten, welcker ghestalt dan sy als hier onder [boven].
Dit soo sijnde, t'stijflichaem IKLM is evewichtich metter water evegroot an NOLM duer het 5^e voorstel, waer duer t'lichaem IKLM, met de rest des waters rondom hem, evewichtich is an een lichaem waters evegroot an ABCD: daerom segghen wy noch naer luyt des voorstels, dat teghen den bodem EF een ghewicht rust, even ande swaerheyt waters die evegroot is met den pilaer, diens grondt EF is, ende hoochde de hanghende lini GE, van t'plat {Plano.} AB, duer t'waters oppervlack AN totten grondt EF:
Waer uyt blijckt dat eenighe drijvende stof in t'water gheleyt, sy en verswaert noch en verlicht (welverstaende als t'water inde selfde hoochde blijft) den grondt niet.

Vorige | Waterdruk 4 | Volgende

Gevolg 2

Laat nu in het water ABCD een voorwerp leggen, of verscheidene voorwerpen, met dezelfde dichtheid als water.
Ik neem ze zo, dat er alleen water blijft binnen IKFELM.

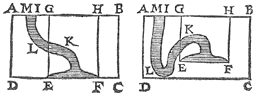
2 bakken, water in smalle vormen met zelfde brede bodem

Dan verzwaren of verlichten deze voorwerpen de bodem EF niet meer dan het water eerst deed.

Daarom zeggen we nog steeds, dat tegen de bodem EF een gewicht rust, gelijk aan de zwaarte van een waterkolom GHFE.

Stevins woorden:

I I V E R V O L G H.

Laet andermael int water ABCD, legghen een styflichaem, ofte verscheyden styflichamen evestofswaer mettet water, ick neem alsoo, datter maer water en blijft als t'begrepen binnen IKFELM;
T'welck so sijnde, dese lichamen en beswaren noch en verlichten den grondt EF niet meer dan t'water eerst en dede:
Daerom segghen wy noch naer luyt des voorstels, dat teghen den bodem EF, een ghewicht rust even ande swaerheydt waters die evegroot is metten pilaer, wiens grondt EF is, ende hoochde de hanghende lini GE, van t'plat AB duer t'waters oppervlack MI, totten grondt EF.

Vorige | Waterdruk 5 | Volgende

Gevolg 3

Laat ABCD weer helemaal water zijn, en EF een bodem evenwijdig met de horizon. Dan duwt het water onder de bodem EF even sterk omhoog, als het water erboven omlaag duwt.
Want als dit niet zo was, zou het zwakste wijken voor het sterkste.

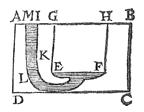bak, water in smalle vorm, nu van onder tegen zelfde bodem

bak, water in smalle vorm, nu van onder tegen zelfde bodem

Leg nu enige voorwerpen met dezelfde dichtheid als water zo, dat het water IKEFLM van onder tegen EF duwt, zoals hiernaast.

Dan duwt het water nu net zo sterk tegen EF als eerst tegen water.

Maar dit duwde even sterk terug, volgens de stelling: Op de bodem EF rust een gewicht, gelijk aan de zwaarte van de waterkolom GHFE.

Stevins woorden:

I I I V E R V O L G H.

Laet wederom ABCD t'eenemael water sijn, ende EF een bodem daer in evewydich vanden sichteinder. T'welck soo wesende, t'water onder den bodem EF, stoot even soo stijf daer teghen opwaert, als t'water boven den bodem EF, daer teghen neerwaert stoot:
Want by aldient soo niet en waer, t'cranckste soude voor t'sterckste wycken, t'welck niet en ghebuert, want yder houdt sijn ghegheven plaets duer het I^e voorstel.
Laet nu eenighe styflichamen evestofswaer mettet water, alsoo gheleyt worden, dattet water IKEFLM, van onder anstoot teghen EF, als hier nevens [boven]. Dit soo sijnde, t'water onder den bodem EF, stoot nu so stijf teghen EF, dat is teghen t'stijflichaem, alst te vooren teghen t'water dede;
maer t'stac daer teghen soo stijf als t'bovenste teghen EF stiet, soo vooren gheseyt is, ende t'bovenste stiet teghen EF naer luydt deses voorstels, daerom t'onderste stoot oock teghen EF naer luydt deses voorstels,
dat is soo wy boven gheseyt hebben, dat teghen den bodem EF noch een ghewicht rust, even ande swaerheyt waters die evegroot is metten pilaer, diens grondt EF is, ende hoochde de hanghende lini GE, van t'plat AB duer t'waters oppervlack MI totten grondt EF.

Vorige | Waterdruk 6 | Volgende

Gevolg 4

Laten we nu de voorwerpen van het 2e en 3e gevolg op hun plaats vasthechten, en het water uitgieten.

Er zal een lege plaats IKFELM blijven, en de basis EF zal geen gewicht dragen.

Hieruit blijkt dat je, als je de lege plaats weer met water volgiet, de basis EF evenzeer zult bezwaren alsof het hele vat ABCD vol water zou zijn (zonder de ingelegde voorwerpen).

Stevins woorden:

Laet ons nu de styflichamen des 2^en ende 3^en vervolghs tot haer plaets hechten, ende t'water uytghieten, ende daer sal een ledighe plaets IKFELM blijven, ende den grondt EF en sal geen ghewicht draghen; waer uyt blijckt, dat met die cleyne ledighe plaets weder vol waters te ghieten, so salmen den grondt EF even so seer beswaren, als of t'gheheele vat ABCD (de ingheleyde styflichamen gheweert sijnde) vol waters waer.

Vorige | Waterdruk 7 | Volgende

Gevolg 5

Maar aangezien de ingelegde voorwerpen van het 2e en 3e gevolg op hun plaats zijn vastgehecht, maakt hun buitenkant niets uit voor verzwaring of verlichting van de basis EF.

Laten we daarom de stof ervan rondom afkorten, zodat alleen de inwendige onregelmatige vormen of vaten MIKFEL overblijven, met water gevuld:

En we zeggen nog steeds, volgens de stelling, dat tegen de bodem EF een gewicht rust, gelijk aan de zwaarte van een waterkolom met als basis die bodem, en als hoogte de loodlijn van het vlak van het wateroppervlak MI tot de basis EF.

En evenzo om de zelfde reden bij alle andere vormen met een horizontale bodem.

Voor meer ondervindingen hiermee zie het begin van de 'Waterwichtdaet' (5 voorbeelden, met tekeningen).

Stevins woorden:
V V E R V O L G H.
Maer anghesien de ingheleyde styflichamen des 2^en ende 3^en veruolghs t'haerder plaets gehecht sijn, soo en gheeft noch en neemt haer uyterste stof tot de beswaring ofte verlichting des grondts EF, daerom laet ons de stof der selver rondtom afcorten, alsoo datter blijven de inwendighe ongheschickte formen ofte vaten met water ghevult MIKFEL, als hier onder [boven].

Ende sullen noch segghen naer luyt des voorstels, dat teghen den bodem EF een ghewicht rust, even ande swaerheyt waters die evegroot is metten pilaer, wiens grondt EF is, ende hoochde de hanghende lini van t'plat duer t'waters oppervlack MI, totten grondt EF. Ende dit alsoo om de selve reden van alle ander formen diens bodems in een plat sijn evewydich vanden sichteinder. [...]
Lees d'ervaringhen hier af breeder inden Anvang der Waterwichtdaet.

Vorige | Waterdruk 8 | Meester Simon