|
dat bestaat uit twee met elkaar verenigde glazen, is gelijkwaardig met een lens, en verzamelt evenwijdige stralen en brengt ze samen in een brandpunt op een afstand van 3 duim van de genoemde voet, dat wil zeggen 4 uncia, 2 scrup. van de Romeinse palm. Verder leidt Huygens daaruit af dat zijn objectiefglas uitstekend is, daar het een zo sterke lens (zoals men zegt) verdraagt, en hij beweert dat voor betrouwbare waarnemingen van Saturnus zulke kijkers en glazen moeten worden gebruikt.
Dit had Huygens makkelijk achterwege kunnen laten; deze regels waren immers niet nodig, aangezien al lang ervoor telescopen waren gemaakt, die zowel wat betreft de lengte, als de vorm van de glazen, als ook de volmaaktheid van het werk, allerminst onderdoen voor die van Huygens; ik heb eens een buis gebruikt die 36 palm lang was, en dus 4 palm, 8 unc. langer dan die van Huygens, en de diameter van de opening was 4 unc. 2 scrup., maar met verwaarlozing van die 2 scrup. wegens het verschil in lengte, namelijk 4 palm, 8 scrup., blijft over dat de diameter van mijn glasschijf {p. 4.} 1 unc. groter was dan de diameter van die van Huygens. En dus is mijn telescoop op dit punt wel te verkiezen boven die van Huygens, volgens een gewone en door iedereen aanvaarde regel; daar namelijk het objectiefglas om zo te zeggen een grotere opening verdraagt.
Bovendien heeft hij geheel zonder reden twee glazen tot een dubbelbol oculairglas samengevoegd; aangezien een enkele lens voldoende is. Ik heb bij de genoemde waarnemingen een lens gebruikt die evenwijdige stralen verzamelt en projecteert in een brandpunt op een afstand van 3 unc. 2 scrup., maar deze afstand is 1 unc. kleiner dan de projectie-afstand van Huygens, dus mijn lens is sterker, terwijl de lengte van mijn kijker groter is. En daar telescopen hierop beoordeeld worden, zoals hij zelf heel juist opmerkt, leid ik zeker met hetzelfde recht daaruit af, dat mijn telescoop voortreffelijker is, en dit om drie redenen. Ten eerste, omdat hij langer is. Ten tweede, omdat hij een objectiefglas heeft dat een grotere opening verdraagt. Ten derde omdat hij een sterkere lens aan kan.
Huygens schrijft op pag. 37 1) van zijn boekje over mij als volgt:
|
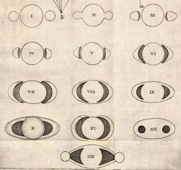
En zulke [hengsels van Saturnus] heeft Eustachio Divini opgetekend in de jaren 1646, 1647 en 1648; de door hem uitgegeven figuur hebben we hier bij nummer 10 weergegeven*); en daar hij voor de meest voortreffelijke kijkermaker wordt gehouden, is te geloven dat hij het aanzicht van Saturnus het zuiverst van allen heeft getekend, behalve dat hij die schaduwen, die in de figuur verschijnen, zelf heeft toegevoegd, naar ik meen.
|
Het is zeker zo, dat ik hem heel dankbaar moet zijn voor deze lof, waarmee hij mij heeft bestempeld als een onbekend en hoogst onnadenkend iemand; maar wat is dat "zelf toegevoegd", anders dan: de mensen op de mouw gespeld? Als het immers van mij komt, is het verzonnen, en dan heb ik Saturnus niet echt zo weergegeven als ik hem heb waargenomen; omdat ik zelf die schaduwen heb toegevoegd, die ik op Saturnus niet gezien heb, en ook niet heb kunnen zien, omdat ze er echt niet zijn op Saturnus; het is dus een fabeltje, een verzinsel; ja zelfs moet het in een zo belangrijke zaak voor mooi bedrog gehouden worden, aangezien de mensen {p. 5.} gemakkelijk erdoor op een dwaalspoor worden gebracht.
|