|
Tacquetio.
|
|
Uw boek 1) en brief, des te meer welkom omdat het vergezeld kwam van een brief van de voortreffelijke Hesius 2), heb ik ontvangen toen ik nog niet hersteld was van een ongelukkige gezondheidstoestand, waardoor het kwam dat ik het niet dadelijk heb kunnen lezen met die aandacht, die dergelijke geschriften verlangen; want nauwelijks enige invloed van ziekte zou hebben kunnen verhinderen, het dadelijk oppervlakkig helemaal door te bladeren. Mijn naam vond ik daar een keer geplaatst en nog eens, en niet zonder lof [p. 7, 49], waarvoor ik u dank zeg en ik zal trachten het overal waar de gelegenheid zich voordoet te vermelden.
Overigens meen ik dat u er heel goed aan hebt gedaan het bewijs van het Theorema van Guldin aan te voeren*); het is immers in de Meetkunde van buitengewoon nut en voordeel. Daarom is hetzelfde enige jaren geleden ook door mij geprobeerd met een methode, niet helemaal gelijk aan die welke u gebruikt hebt, naar ik zie. Ik kwam ook op dezelfde gedachte als u, toen ik een lijn trok door het zwaartepunt van een halve hyperbool, en ik heb niet alleen aangetoond dat de verhouding van AO tot QO in uw figuur 50 °) gegeven is, maar wat die was heb ik ook berekend, wat helemaal niet moeilijk is.
1) Cylindricorum et Annularium liber quintus. Zie brief No. 102, n.5 [I-IV: 1651, V: 1659].
2) Zie brief No. 689.
[ *) Zie Tacquet, 1659, p. 2, 75 en fig. 34.]
[ °) Fig. 50 bij Prop. XLV, p. 65.]
|
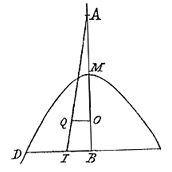Zie hier twee gevallen voor u, en wel:
- wanneer de helft AM van het latus transversum*) gelijk is aan de as MB, zal AO tot OQ °) staan als AB tot 4/9 BD, dat wil zeggen dan zal BI zijn 4/9 BD;
- doch wanneer AM gelijk is aan de helft van MB, zal BI zijn 15/32 BD.
Het kan lijken dat dit tot op zekere hoogte nuttig is voor de kwadratuur van de hyperbool, maar stellig wordt niets daaruit minder tot stand gebracht, zoals ook niet uit al het overige dat u in uw boek aanvoert, ook al zijn die dingen op zichzelf mooi en het beschouwen waard. En zeker uitstekend leek mij onder andere dat over een gedeelte van een hyperbolisch prisma herleid tot een kubus [p. 73], wat velen zeer wonderlijk zal lijken.
Verder vind ik uw manier van bewijzen overal duidelijk en nauwkeurig, en dat prijs ik, behalve dat ik in het bewijs van propositie 4 in boek 5 datzelfde mis, waarvan ik, als ik me niet vergis, eerder heb gezegd [<] dat het ontbreekt in andere bewijzen van u van deze soort. Ik zou namelijk willen dat u na het tegengestelde te hebben aangetoond van wat gesteld wordt, zou toevoegen wat absurd is, en daaruit zou concluderen dat de stelling waar is, zoals Euclides heeft gedaan in propositie 12 van boek 9 3). En u zult tocn niet geloven dat hij dit dit zonder reden heeft gedaan.
|
Ik weet dat het moeilijk is zich los te maken van een al lang geleden aangenomen en verdedigde mening, vooral omdat het ons niet past bij de principes zelf. U zegt namelijk [<] dat het met natuurlijk licht heel klaarblijkelijk is dat datgene waar is, waarvan het veronderstelde tegendeel zichzelf vernietigt. Doch dit lijkt me niet anders duidelijk te zijn dan wanneer ik mijn aandacht richt op een herleiding tot het onmogelijke, met behulp waarvan gemakkelijk onomstotelijk de waarheid kan worden bewezen van wat door u als een axioma wordt gesteld. Ook lijkt me, wat betreft dit bewijs van u van propositie 4, zoals ook wat betreft die propositie 35 van boek 5 van de Elementa Geometriae [1654], dat de redenering hiervan heel anders is dan die van Euclides in propositie 12 van boek 9. Aangezien daarin de foute of tegengestelde positie zodanig in het bewijs komt, dat de bewijsvoering zelf eruit voortkomt, wat bij die van u anders is. Nergens immers in dit heel nieuwe bewijs van u
[ *) A is middelpunt van de 2 takken van de hyperbool, M is één van de toppen; met 'latus transversum' werd bedoeld de afstand van top naar top.]
[ °) Q is het zwaartepunt van de halve hyperbool BDM, zie p. 66.]
3) Tacquet verzorgde zelf een Euclides-editie: Elementa geometriae planae ac solidae, Antw. 1654 [zonder de boeken 7 t/m 10, zie p. 220. In ed. Clavius 1607, p. 134: "Quod est absurdum. ... ergo ... Quod ostendenum erat".
In het Grieks, ed. Basel 1533, p. 121: 'adunaton' voor "absurdum".]
|
|
beschouwt u een geval waarin de hoogte M groter of kleiner is dan de weg van het middelpunt O; en zo zou niets makkelijker zijn, meen ik, dan dit bewijs in een gewoon rechtstreeks bewijs te veranderen. Of althans, nadat u aan het eind had gezegd "Dus de hoogte M en de weg van het middelpunt O zijn gelijk", had u meteen als volgt kunnen besluiten: "Maar dit is absurd, daar ze ongelijk zijn gesteld. Dus enz."
|
|
Maar ik blijf nu te lang hierbij hangen, en ik zou willen dat u het opvat, voortreffelijke heer, als iets dat gezegd is om te oefenen en om u te laten zien dat ik uw geschriften niet haastig doorneem maar zorgvuldig overwegend; ik hoop ten zeerste dat het bij de mijne door u wordt gedaan.
|
|
Niet zo lang geleden heb ik aan de eerwaarde pater Gregorius enkele theorema's 4) gestuurd, maar zonder bewijs, over conoïdische en sferische oppervlakken, waarvan voor u misschien een kopie is gemaakt, anders zou ik willen dat u hem erom vraagt, aangezien ik er niet aan twijfel dat ze u zullen bevallen. Ik weet niet wanneer er tijd zal zijn om deze uit te geven; daar er steeds weer andere dingen opkomen die me ervan afhouden de vorige af te maken*).
|
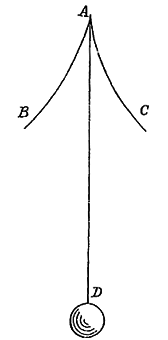Een heel nieuwe uitvinding heb ik nu waarmee ik de heen en weer gaande bewegingen van een slinger onderling precies gelijk maak. Ik heb namelijk een bepaalde kromme lijn gevonden volgens welke de hoorntjes of plaatjes AB en AC, waartussen de slinger beweegt, moeten worden gebogen, om alle slingeringen isochroon te maken, terwijl anders een verschil daartussen merkbaar is.
Het ga u goed, voortreffelijke heer en houd mij op uw beurt op de hoogte van uw studies en wat u voor nieuws onder handen hebt. Afgegeven op 1 januari van het jaar 1660, moge het voor u gelukkig zijn.
4) Zie het stuk No. 678.
[ *) Zie hier een lijstje met voornemens om de Dioptrica uit te geven, 1653-1661.]
|
No 766.
Christiaan Huygens aan [A. Tacquet].
3 augustus 1660 (Concept).
|
| 3 Augusti 1660.
|
| Reverende et Clarissime Vir
Ik zou me erover schamen dat ik niet eerder de belofte heb vervuld, als ik niet een gegronde verontschuldiging voor dit oponthoud zou kunnen aanvoeren; toen ik namelijk na mijn terugkeer uit Antwerpen 1) bij een Engelse boekhandelaar 2), waar ik eerder het boekje 3) van Wallis te koop had zien staan, daarnaar had gevraagd, zei hij dat hij er geen kon leveren omdat hij ze alle naar de Frankfurter Buchmesse had gezonden. Zo zou er nog langer op gewacht moeten worden, als ik niet tenslotte dit Leidse exemplaar op de kop had getikt, dat u met deze brief wordt geleverd. U zult daarin inderdaad zowel uitstekende als niet weinige vondsten vinden; en verder met hoeveel geestdrift de Engelsman moeite doet zichzelf en de zijnen lof toe te brengen, tegen de Franse Meetkundigen. Toch weet ik niet of hij zich overal wel voldoende oprecht heeft gedragen. Zeker na het zien van het boek van Dettonville 4) kon hij het meeste daaruit zich eigen maken, en datgene verbeteren waarin hij eerst de weg was kwijt geraakt. En het was voor hem niet heel moeilijk
1) Zie over deze reis naar Antwerpen [28 juni - 8 juli], waar Chr. Huygens Tacquet zal hebben bezocht, brief No. 760, n.1.
2) Samuel Broun, zie brief No. 307, n.1.
3) Tractatus duo ... De cycloide, 1659. Zie brief No. 690, n.3.
4) Blaise Pascal, Lettres de A. Dettonville, 1659. Zie brief No. 560, n.32.
|
|
nadat hij mijn theorema's over oppervlakken van conoïden en sferoïden 5) had ontvangen, hetzelfde ook op zijn manier te onderzoeken. Zoals ook niet de afmeting van die kromme die al lang hiervoor en als eerste van allen door onze Heuraet bekend was gemaakt, en gepubliceerd. Maar tot zover hierover.
Het boek 6) dat u mij had gegeven en aangeraden te lezen, en waarvan de schrijver niet onwelsprekend en niet ongeleerd lijkt te zijn, behandelt toch niet de belangrijkste geschilpunten van alle die er tussen ons zijn, en bij wat hij schrijft om het offer van de Mis te onderbouwen lijkt zijn bewijsvoering me wel zeer bezwaarlijk. Wat zal ik nu in het algemeen zeggen, beste Tacquet! Als het met redenen gedaan moet worden, weet ik niet of jullie voldoend geldige kunnen vinden, om mij te overtuigen van meningen van zo groot gewicht. Jullie voeren immers de autoriteit van boeken aan waarvan de tekst bedorven kan zijn, van mensen die zich vergist kunnen hebben; hoe ver is dit alles dan ook verwijderd van de evidentie van Meetkundige bewijzen! Hieraan ben ik al lang gewend geraakt en ook hierop vertrouw ik soms nauwelijks voldoende, als ze niet heel goed doorzien zijn; en daar deze nu gaan over dingen van weinig gewicht, wat denkt u dan dat erbij komt in deze meer belangrijke zaken? |
|
Maar u zegt immers dat we niet zozeer op de rechte weg gezet worden met de rede als gids, als wel met hulp van de Heilige Geest. Ik ben het met u eens en laten we dus op hem vertrouwen. Maar als hij me niets heeft ingegeven waarom ik afstand moet doen van mijn oorspronkelijke religie, zult U mij hierom wel ongelukkig achten, ikzelf echter allerminst. Ja juist des te gelukkiger, omdat wat ik vanaf mijn vroegste jeugd voor waar heb gehouden, ook nu als zodanig beschouwd kan worden. Het ga u goed en blijf genegen
Tui observantissimum
5) Zie het stuk No. 678.
6) Zie brief No. 767, n.2 [hierna: Hazart; bespreking van deze discussie in: Georges Monchamp, 'Les correspondants belges du grand Huygens', in Bulletin de l'Académie royale des sciences, des lettres et des beaux-arts de Belgique 1894 - No. 2, p. 295-298].
|
No 767.
A. Tacquet aan Christiaan Huygens.
7 augustus 1660.
|
| Nobilissime Hugeni
Uw brief heb ik vanmiddag tegen 6 uur ontvangen, samen met het boek 1) van Wallis, voor welk geschenk ik u heel veel dank zeg; ik ben terstond begonnen het door te nemen, en dat zal ik later ook nauwkeuriger doen.
1) Tractatus duo ... De cycloide, 1659. Zie brief No. 690, n.3.
|
|
Ik ben blij dat ons geschenkje U van uw kant niet heeft mishaagd, namelijk het boekje 2) van Cornelius Hazaert 3), en dat het door u is doorgelezen. Deze schrijver heeft voornamelijk op het oog gehad, aan te tonen dat de riten en ceremoniën die de Heilige Kerk gebruikt, door de uwen veroordeeld als bijgeloof en afgodendienst, overeenkomen met de riten en ceremoniën van die Kerk, die de eerte 400 jaar na Christus in stand is gebleven, en waarvan de uwen erkennen dat het de onbedorven en ware kerk van Christus is geweest. Wat hij inderdaad uitstekend heeft gedaan op grond van getuigenissen van alle Vaders, die in de eerste 400 jaar hebben geleefd. En een feitelijke kwestie kan niet anders bewezen worden. Dan is het noodzakelijk dat daar deze twee dingen uit volgen: het ene is, dat die riten vrij zijn van alle afgodendienst en bijgeloof; het tweede, dat jullie kerk verschillend is van die eerste, dat wil zeggen van de ware; daar die van jullie dingen verwerpt, als zijnde vol afgodendienst, die de eerste als vroom en heilig heeft toegepast.
|
|
Tenslotte, als het met redenen gedaan moet worden, vreest u dat er geen voldoend geldige gevonden kunnen worden, en u zegt dat dit alles ver verwijderd is van de zekerheid van meetkundige bewijzen, waaraan u gewend bent. Steunt die secte die u tot nu toe hebt aangehangen dan wel op zulke bewijzen? Onderzoek die eens, alstublieft, weeg ze af en vergelijk ze met de onze; u zult vinden dat ze zodanig zijn, dat ze niet alleen niet dwingen tot instemming, maar voor een verstandig iemand zelfs niet waarschijnlijk kunnen lijken. En dat ook heel waar is, wat ik u bij ons samenzijn vaker heb verzekerd, begrijpt u: daar er slechts één ware Kerk is, waarbuiten niemand behouden kan zijn, zult u ongetwijfeld eeuwig verloren gaan, als u het leven beëindigt in uw secte. Maar dit verzoek ik u, mijn Huygens, dat u het niet te scherp opvat wat hier gezegd is; het is een weergave van een zekere waarheid, en een oprechte liefde voor u en ook een geweldig verlangen naar uw heil.
|
Ik ben er nu echter niet op uit, verder met u over Religie te twisten; maar ik wens vurig, dat u zelf, langs een weg die veel aangenamer is, geholpen door de Goddelijke genade, de waarheid verwerft. Wat wel een keer zal gebeuren, naar ik vertrouw, als u hartstochtelijk en in ernst de Goddelijke hulp aanroept. Wie verder verlangt dat zijn gebeden door God verhoord worden, behoort zodanig gezind te zijn, dat hij zijn zonden, waarmee hij die onbegrensde Majesteit heel vaak heeft beledigd, met een waarachtig voornemen ter verbetering, oprecht betreurt; en dat hij het zich wegens die zonden in het geheel niet waard acht, dat God hem enige gunst betoont, en niettemin vertrouwt op zijn onmetelijke goedheid en barmhartigheid. Naar wie, zegt immers God zelf bij Jesaja [66.2], zal ik omkijken dan naar de behoeftige en deemoedige en degene die siddert voor mijn woorden? Als u zich, zo voorbereid om tot de Almachtige te bidden, volhardend
2) Vytwendighen handel ofte Cerimonien van de H. Roomsche Kercke aengaende den H. dienst van de Misse ..., Antw. 1659 [T. p.]. De 4e druk verscheen in 1661.
3) Cornelius Hazart ... 1617-1690, werd in 1635 jezuïet, en was ijverig twistredenaar, getuige zijn vele geschriften. [30 in UB Paderborn.]
|
|
en dikwijls tot hem wendt, twijfel ik er volstrekt niet aan, of u zult met het licht dat uit de hemel komt een keer uit die duisternis van dwalingen te voorschijn komen. Deze hoop zal worden ondersteund door het boekje 4) dat ik met deze brief aan u stuur, en ik verzoek u het met het oog op uw heil nauwkeurig en geheel door te lezen, en er geen bezwaar tegen te hebben (als u van plan bent naar Parijs te gaan) het mee te nemen voor onderweg. Lees vervolgens zo u wilt een katholieke schrijver over geschillen; ik zou u aanraden het Manuale controversiarum 5) te gebruiken, van Martinus Becanus 6) van onze Sociëteit; het is namelijk duidelijk, nauwkeurig en geenszins breedvoerig; het is een boek in quarto. En als u het ook binnenkort met een geleerd iemand bespreekt, zal daaruit het meeste voordeel komen. In Parijs zult u zowel van andere soorten mensen, als van onze Sociëteit mannen vinden die uitnemend zijn in vroomheid en in de letteren, en als u met hen zult omgaan zult u er allerminst spijt van krijgen, denk ik.
|
|
Dit is het, voortreffelijke Huygens, waarvan ik heb gemeend, aangezet door een zeer oprechte genegenheid tot u en belangstelling voor u, dat door mij voor u moest worden opgeschreven. Misschien zal het u lijken dat ik in heel deze zaak wat onbeschaamder ben geweest dan zou behoren. Maar, ofschoon ik schat dat u er veeleer een ander oordeel over hebt, als het toch zo is, wil ik liever dat u het nu inderdaad zo voelt, dan dat u op de dag van het laatste oordeel bij de eeuwige rechter mij ervan beschuldigt, dat degene die in de Meetkunde en de studies zoveel heeft bijgedragen, een vriend in de steek heeft gelaten inzake de eeuwigheid. Ondertussen zal ik doorgaan u niet alleen genegen te zijn, maar ook in volhardende gebeden God te smeken om uw heil. Het ga u goed.
|
| Tuus in Christo servus
|
| And. Tacquet e Societate Jesu.
|
| Antwerpen 7 juli 7) 1660.
4) Misschien: Corn. Hazart, Victorie van Roomen over Geneve in't stuck van't aen-roepen ende eeren der heylighen. Behaelt door het sweert des gheests t'welck is het woort Godts, Ephes. Cap. 6. vers. 17., Antw. 1660.
5) Manuale controversiarum huius temporis ..., Herb. 1623. {Ed. 1624 in Cat.'87, 4.48.]
6) Martinus van der Beek (Becanus) ... 1563-1624, werd jezuïet in 1583; hij onderwees theologie te Würtzburg, Mainz en vanaf 1602 te Wenen. Hij was doctor in de artes en de theologie en publiceerde veel werken over geschillen.
7) Tacquet zal zich hebben vergist in de maand; de brief is duidelijk een antwoord op brief No. 766 van 3 augustus.
|