Manuscrit A (1659).

Vid. Cartesij Meteora pag. 249*). Materia subtilis in guttis circumagitur quae facit ut rotundae sint, unde si calidius caeteris partibus sit spatium BAC per totum circuitum is calor propagatur in gyrum actus, atque ita impedit ne gelu astringatur exterior guttae portio.

[ 475 ]

[ v ]

sed cylindri tamen toti liquidi esse non possunt, ac deinde interius gelari. quia liquidi dum sunt in guttas rotundas abijssent. Ergo potius toti glacie constant ab initio, deinde exteriora liquescunt.   cum autem liquefacta fuerint, gelari denuo facile nequeunt ob calorem coni BAC, per totum circuitum se diffundentem°).   *)  Ed. 1644. Descartes y parle de la formation d'une goutte. Dans le texte français (Discours Cinquiesme "Des Nues" [1637, 204], Adam et Tannery, t. VI, p. 280) on lit. e. a.: la matiere subtile .. doit tournoyer au dedans de cette goutte, & aussy en dehors en l'air qui l'enuironne, mais d'autre mesure qu'au dedans, &, par ce moyen, disposer en rond toutes les parties de sa superficie. Apparemment Huygens adopte ici l'idée de la matière subtile tournoyant dans les gouttes.   °)  Dans une partie biffée du § 5 [<] du Traité Huygens écrit à propos du cône BAC: Dese warmte nu wert door het gansche water gecommuniceert, waer door gebeurt dat alhoewel weder een koude lucht den droppel komt te omringen, dit water daer door niet lichtelyck weer bevrosen kan werden. Daer en boven schijnt dat de selfde warmte oorsaeck is dat den binnenste kern niet verder en ontdoyt, als de koude nae binnen jaegende, gelyck men veeltydts siet in de winter dat het binnens huys meest vriest als 't buyten begint te doyen, en gelyck men om ijs door sneeuw en sout te maecken, het vas met water daer dat om geleght is, ontrent het vier set om te beter te doen bevriesen. [Cf. Isaac Beeckman, II, 5.]

[ 476 ]

[ v ]

Manuscrit K.

§ 1.   17 Jan. 1660. hora 3½ pom. Nivem sexangulam observavi. Nix minuta ac densissima cadebat in qua plurimi flocci stellularum instar, reliqua nix minoribus particulis constabat et veluti stellulis dissolutis. Nam et foliolum unum atque alterum in aliquibus deerat. Forma integrarum et magnitudo erat fere hujusmodi.   Erant autem planissimae et tenuissimae, et ad centrum nihilo quam alibi solidiores. et calore liquefactae exiguam aquae guttulam efficiebant velut semen rapae. 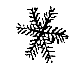Capillamenta foliorum ita disposita erant, ut hac majuscula figura expressa sunt ut nimirum singula radijs proximis essent parallela. quod microscopio clarissime patebat. radij in aliquibus inaequali longitudine erant sed anguli ad centrum exacte omnes gr. 60.   [<]   Erasmius Bartholinus alias etiam figuras observavit hujusmodi, dissertatione de figura nivis, impr. 1661*).   § 2.   1663. 9 Jan. hora 11½ ante meridiem. Vitrum aqua pluvia plenum in musaeo per noctem steterat erat autem gelu intensum foris, aere sereno, vento ab oriente spirante. in vitro nulla tamen glacies erat, sed aqua limpidissima et liquidissima remanserat. Cum vero in mensa vitrum deposuissem, ubi juxta foculus cum paucis prunis ex cespite forte adstabat momento citius aquam omnem glacie refertam animadverti°). Erant autem glaciei laminae tenuissimae pollicem atque eo amplius latae, planitie vero exactissima; ac sine ordine ullo per omnem aquae profunditatem dispositae cernebantur, et suo quaeque loco fixae.

[ 477 ]

[ v ]

Extractis earum compluribus inveni simili ratione constructas ac sexangulae nivis foliola quae saepius observaram. Habebant enim radios veluti quosdam e quibus singulis alij multi utrinque protendebantur, angulo 60 graduum inclinati, quibus circa oras liquefactis, denticuli cernebantur, ordine atque aequis distantijs.

§ 3.   16 Jan. 1665. Urinam mane gelatam inveni, atque in superficie duas sex radiorum stellas perfectas, angulis ad centrum prorsus aequalibus, praeter imperfectas aliquot et folia qualia in observatione superiori.   *)  Cet alinéa fut évidemment ajouté plus tard. La brochure mentionnée est intitulée: "Erasmi Bartholini D. & P. P. De figura nivis dissertatio, Hafniae, Typis Matthiae Godicchii, Sumptibus P. Hauboldi, Anno MDCLXI" [T. p.]. Huygens copie ici plusieurs figures de la brochure de Bartholinus.   °)  Huygens semble ne pas connaître le phénomène du retardement de la congélation, puisqu'il attribue la congélation subite de l'eau à l'action de la chaleur des "prunae ex cespite"; il s'agit sans doute de tourbes. Comparez la note °) de la p. 475.

[ 478 ]

[ v ]

Manuscrit A.

haec neque invenire possunt neque inventa intelligere.

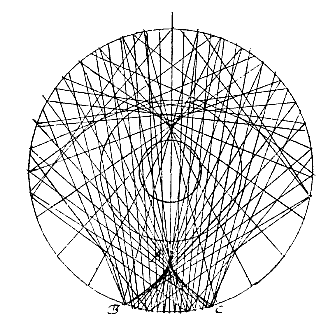
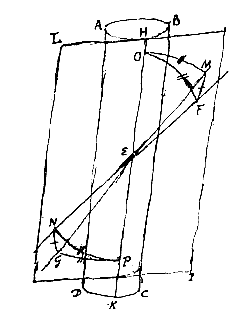§ 1.   Ad demonstrationem brevissimam circuli albi, qui horizonti parallelus in pareliorum phaenomenis. In Cylindrum ABCD perpendiculariter erectum incidat radius a solis centro adveniens FE, qui reflectatur secundum rectam EG. dico FE, EG aequalibus angulis inclinari ad planum horizontis. Sit enim latus cylindri per punctum reflexionis E ductum HK, secundum quod tangi cylindrus intelligatur plano LI. Constat itaque radium FE eodem modo a plano hoc reflecti atque a cylindro ABCD, hoc enim in dioptricis axiomatis loco est qualiscunque fuerit curva superficies reflectens. Quod si jam plano LI aliud planum ad rectos angulos insistere ponatur, quod in se contineat radios FE, EG, constat etiam ex legibus dioptricis utriusque plani communem intersectionem, quae sit recta MN, transire per punctum reflexionis E, angulosque aequales esse FEM, GEN. Intelligatur itaque sphaerica superficies cujus E centrum, quae abscindat rectas aequales EF, EM, EO, itemque EG, EN, EP, quarum nempe EO, EP sint in recta HK. Sintque circulorum maximorum in sphaerae superficie arcus FO, FM, OM; itemque GP, GN, PN. Quia igitur planum per FMNG ductum rectum est ad planum LI, et utrumque per sphaerae centrum E transit; sunt autem in plano per FMNG arcus FM, GN; et in plano LI arcus MO, NP; erunt in triangulo sphaerico FMO rectus angulus M, et in triangulo GNP rectus angulus N. latus autem MO aequale est lateri NP, quia angulus MEO aequalis NEP.

[ 479 ]

[ v ]

Itemque latus MF aequale lateri GN, quia aequales anguli FEM, GEN. Itaque et latus reliquum FO aequale erit lateri reliquo GP. ac proinde angulus FEO aequalis angulo GEP. Quorum complementa ad angulum rectum cum sint anguli inclinationis ad horizontem radiorum FE, EG etiam isti inclinationis ad horizontem anguli aequales erunt. quod erat demonstrandum.   Eadem est demonstratio cum radius FE est intra cylindrum, et a superficie ejus reflectitur quod ad parelia pertinet ut ostendatur ea in circulo albo cerni debere [<]. Parhélies latéraux   § 2.   [...]*)   [ *)  Figure 14 de la Tab. V des "Opuscula Postuma" et formule de C. Visser (add. p. 550).]

[ 480 ]

[ v ]

Chartae astronomicae [HUG 31, 70r].

Ad inveniendum angulum verticalium circulorum per solem et per parelium alterutrum quod soli est a latere [<].   sit solis altitudo 10°.

s[ubtrahendo]. 9.2396702 log. sinus altit.s : cujus cape et log. sin compl.i 9.9933515 0.1260984 diff. log. 187 et 250 quae est proportio refractionis aquae. ————————— 9.1135718 log. sinus anguli.

[ 481 ]

[ v ]

9.9963018 log. sin. compl.i anguli praecedentis. s. 9.9933515 log. s. c. altit. . ————————— 0,0029503 ad. 0.1260984 diff. log. 187 et 250. ————————— 0.1290487 hic numerus est pro differentia log. terminorum proportionis refractionis quae cylindro convenit in hac altitudine. vide pag. 7 in fine libri A. ad. 9.6749194 log. sin. / ADC inventi pag. praec.i qui semper idem, posita crassitudine cylindri aquei ad glaciatum quae 1000 ad 473. quae nempe requiritur ut corona appareat 44 gr. ————————— 9.8039681 s. c. ..... 50.27' s. ex compl.o / ADC 61.46' compl. 28.14. —————— 11.19 2 —————— 22°38' quaesitus angulus circulorum verticalium per solem et parelium a latere.

[ 482 ]

[ v ]

Manuscrit A.

§ 3.   / MCB supponitur, inde inveniuntur / BAE altitudo . et / CLP, qui est arcus horizontis interceptus inter verticalem per et verticalem per parelium. assumitur autem cylindri glaciati certa crassitudo, ad cylindrum aqueum ut hic subdupla.

[ 483 ]

[ v ]

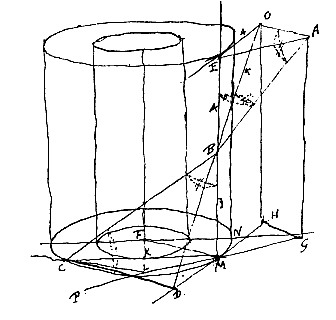
Paradigma. / MCB 12 gr.
  9.9375306  sin. c. / MCD semper idem, quia pendet a proportione crassitudinis
             cylindri glaciati ad cylindrum aqueum. hic ponitur semper 30 gr.
  9.9904044  sin. c. / MCB
———————————
1|9.9279350  sin. c. 32.6 / BCD. ejus sin. .53139
                                                4
                                          ———————
                                          2.12556
                                          3
                                          ———————
                                           .70852  sin. 45.7. / BAO. 

[ 484 ]

[ v ]

9.3178798 sin. / BCM 9.7254203 sin. / BCD s. ————————— 9.5924586 sin. / DBM sive EBO 66.58'. 9.5924586 sin. c. / EBO 9.8503675 sin. / BAO ——————————— 1|9.4428261 sin. / BAE 16.6' altitudo . 9.8485988 sin. c. / BAO 9.9826235 sin. c. / BAE ————————— 9.8659753 sin. / AEO vel GMH 47.16' ex CMD 60.0 ——————————— / CML 12.44' / CLP 25.28'.

Chartae astronomicae [HUG 31, 68r].

angulus verticalium circulorum quaeritur per et parelium laterale transeuntium cum cylindrus aqueus est ad glaciatum secundum diametrum ut 1000 ad 680.

ut 1000 ad 680. sin. 42.49' altitudo 10° log. 9.83229 .12905 log. Refr. in hac altitudine. 9.83229 47.11 +) ——————— 9.96134 s. c. 23.49 ————— 23.22' 2 ————— 46.44 later.

[ 485 ]

[ v ]

Manuscrit A.

Parhélies posterieurs   § 4.   CDF horizon. A spectator. Z zenith. / BAC altitudo parelij aequalis altitudini solis. ZD circulus verticalis inter duo parelia medius transiens.

[ 486 ]

[ v ]

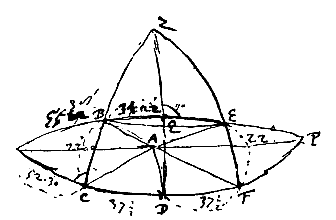
ZBC, ZEF circuli verticales per parelia transeuntes.   Haec sunt parelia quae in parte coeli quae soli opposita est spectantur.   Cum angulus BAC hoc est altitudo solis veri supra horizontem est 22 gr. invenio angulum DAC vel DAF gr. 37½. unde distantia pareliorum erit 68°44'.   Cum angulus BAC est 18° invenio DAC 40.0'.   Cum BAC 10½ fit DAC 41½.   Cylindro aqua pleno [<] hos angulos quaesivi.

10°30 41.30 25.30 35.0 18.0 40. 26.45 34.15 / BAC 22. / DAC 37.30 / BAC 27.15 / DAC 34.0 22°30 36.15 27.30 33.30 24.15 35.30 28.30 32.30 / BAC 30.45 / DAC 31.30 31.30 32.0 33.30 28.0 34. 27.15 35. 26.30 36. 25. 36.30 24.15 44.0 18.0

Si sol altior 58 circiter gradibus non poterunt apparere duo soles oppositi soli vero.

[ 487 ]

[ v ]

[...]*)   [ *)  Figure 19 de la p. 415 et formule de C. Visser (add. p. 550).]

[ 488 ]

[ v ]

Chartae astronomicae [HUG 31, 70r].

ad inveniendum angulum verticalium circulorum per solem et per parelium alterutrum eorum quae soli sunt ex adverso.   Ponatur altitudo eadem quae in quaestione praec. 10 gr. [<].

0.1290487 log.s Refractionis in hac altitudine. 10.0000000 log. Radij. ad. —————————— 10.1290487 0.3010300 log. 2. brevitas gratia possit addi s. —————————— log. radij minus log. 2. 9.8280187 log. sinus anguli. nempe 9.6989700

[ 489 ]

9.8690152 log. sin. c. praeced.is angi. 0.3010300 log. 2. ad. —————————— 10.1700452 .2385606 log. \/3 sive 1/2 log. 3. posset brevitatis gratia addi s. —————————— log. 2 - log. \/3 9.9314846 sin. .... nempe 0,0624694. 0.1290487 log. Refract.is. s. —————————— 9.8024359 sin. 29.23 2 ————— 78.46 58.39 s. ————— 20. 7 2 ————— 40.14 angulus quaesitus.

Haec est Regula ad Iridis diametrum ex data proportione refractionis inveniendam sed ad logarithmos accommodata.

[ 490 ]

[ v ]

Chartae astronomicae [HUG 31] f. 66.

Arcs inverses   § 5.

[ Fig. 59 ]  [<]

90. 0 HR in parel. Rom. 1630 [<] est 76.10 —————— (- RA 13.50' DR. 47.40' DH. 28.30' / RAN arc. HC. 48.16' modo inventum.

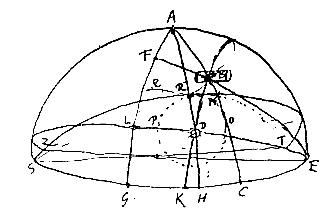
ad examinandum an in parelio Romano 1630, arcus quidam HRC (in fig. parelij [<]) hic autem QRB inverso situ tangere debuerit coronam PRO. Quaerendum punctum aliquod in arcu QRB.

[ 491 ]

[ v ]

Chartae astronomicae [HUG 31] f. 67.

[ Fig. 56 ]

/ MCB. 12.0'.
  MCD. 44.

  9.8569341  sin. c. MCD semper idem.
  9.9904044  sin. c. MCB.
———————————
1|9.8473385  si. c. 45°17' BCD. ejus sinus  71059
                                                4
                                          ———————
                                          2.84216
                                          3
                                          ———————
                                            94739  sin. 71.20' BAO.

[ 492 ]

[ v ]

1|9.3178789 s. BCM. 9.8516220 s. BCD; ——————————— sin. c. 9.4662569. 72.59 DBM, EBO. 9.9765318 sin. BAO. ——————————— 1|9.4427887 sin. 16.6'. BAE altitudo super basin cylindri. DL [Fig. 59] 16.6'. 1|9.5052339 s. c. BAO [Fig. 56] 19.28' AEO 9.9826235 s. c. BAE ex 46. 0 CMD ——————————— ————————— 9.5226104 s. AEO 26.32 CML 2 ————————— 53.4 CLP.

[ 493 ]

[ v ]

[ Fig. 59 ]

  BD, LF. 53.4'

                 90.0                 1|9.4429728  sin. 16°6' DL  BF.
    altitudo                          9.9438985  sin. AD.
supra horizontem 28.30                ———————————
                 —————                  9.4990743. sin. / LAD 18.24'.
             AD. 61.30

1|9.6786629  sin. c. AD.                9.9966096  sin. c. AF
  9.9826235  sin. c. LD.                9.9826235  sin. c. BF
———————————                           ———————————
  9.6960394  sin. c. AL, 60.13.       1|9.9792331  sin. c. AB. 17.35'
                     LF  53. 4
                         —————
                     AF   7. 9
1|9.4603492  t. BF
  9.0950556  s. AF
———————————
 10.3652936  t. 66.4° FAB
                18.24 LAD
                —————————
                48.16' HC

[ 494 ]

[ v ]

Chartae astronomicae [HUG 31] f. 66.

1|9.3913595 t. AR. 20.18' AN 9.8232554 s. c. RAN. 17.35' AB ——————————— —————————— 9.5681041 t. AN. 2.43' BN.

Quaeritur aliud punctum in arcu QRB .... / MCB [Fig. 56] 6.0' .... HC. 24.35' .... BN. 0.36'.   Haec puncta inventa sunt hoc modo, ut non opus sit uti linea curva illa quae describitur ope tabellae prius constructae qualis in princ. pag. 9. neque etiam tabella ipsa.   Huygens avait en effet commencé par calculer pour une autre hauteur du soleil (savoir 10°) au-dessus de l'horizon véritable un certain nombre de valeurs correspondantes pour les arcs DL et DB de la Fig. 59, et voulait trouver pour cette hauteur du soleil d'autres valeurs de DB par interpolation:

[ 495 ]

[ v ]

il est fort possible qu'il se soit en effet servi de ce système pour déterminer approximativement un nombre de points des arcs inverses suffisant pour établir leur forme pour différentes hauteurs du soleil. Il dit dans un calcul de la f. 67 v. (portant le no. 9): hic arcus DB invenitur ex cognito arcu DL: non autem calculo invenitur sed ope lineae curvae descriptae auxilio tabellae quae initio hujus paginae habetur. Voici cette tabelle pour la hauteur du soleil de 10°: Altitudo / CLP [Fig. 56] 0' 23.38' 7.50 24.6 16.6 25.28 24.20 28.12 32.50 32.52 41.48 41.34 51.36 60.26 extra ord. 59.0 104.30 où Huygens annote en marge: Si ad figuram paginae hujus vel pag. 11 [Fig. 59 de la f. 66] hi numeri referantur Altitudo significat altitudinem supra basin cylindri hoc est arcum DL. et pro arcu CLP venit arcus LF, vel in minore circulo arcus DB. Circulus magnus ALG intelligitur is esse quem facit planum baseos cylindri aquei continuatum, ipse autem cylindrus axem habet horizontis plano parallelum.

Chartae astronomicae [HUG 31] f. 69.

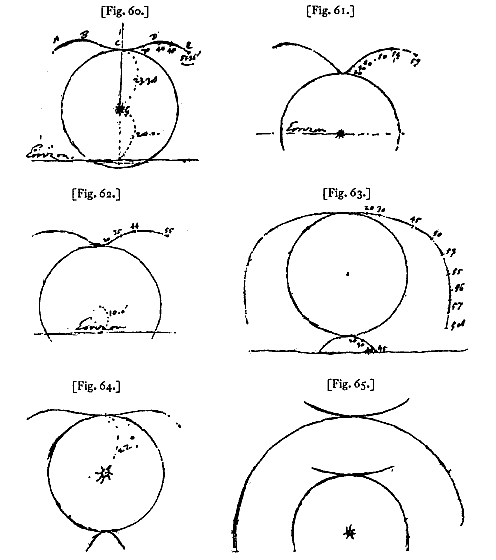
Figura arcus inversi in parelio Heveliano [<] sole alto 20 gr. [Fig. 60], sed tantum pars BCD apparuit, reliquas BA, DE, semper debiliores esse necesse est, idque quo magis a puncto medio C remotae sunt. Pono hic semid. coronae fuisse 23.38*), licet Hevelius dicat paulo minorem fuisse. nam non multum refert.   Numeri curvis arcubus ascripti sunt gradus altitudinis solis supra bases cylindri, qui ijs in locis arcus videri faciunt. cum autem major est ea altitudo quam 35 vel 40 forsan graduum nimis debilis fit lux ad efficiendos arcus, unde vix unquam puto partes ulteriores arcuum horum, nempe ultra num. 40 cernuntur.   Hic quoque {Fig. 61] ut in superiori ponitur cylindrus glaciatus diametro subdupla ad aqueum. Sol autem in horizonte.   Sole alto 10 gr. [Fig. 62].   Sole alto gr. 30 [Fig. 63].   alt. 27. [Fig. 64].   alt. 25° [Fig. 65].   *)  23° 38' est la valeur du rayon correspondant à m = 1 : 2 (rayon du noyau du cylindre à celui du cylindre lui-même) et n = 4/3 (indice de réfraction).

[ 496 ]

[ v ]

[ Cf. III, 316, lettre à Hevelius, 22 août 1661.   Simulation: 'Tangent arcs'.]