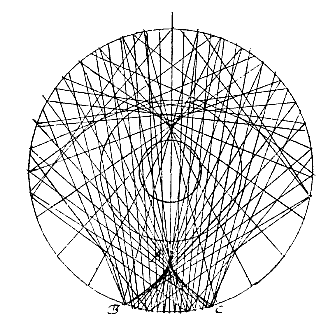
VIII: druppel , IX: sneeuwkristal , X: meetkundige bewijzen , omgekeerde boog
| [ 474 ] | OC |

| Zie Descartes' Meteora, pag. 249*). Subtiele materie draait rond in de druppels, wat maakt dat ze rond zijn, en daarom, als de ruimte BAC warmer is dan de overige delen, wordt die warmte over de hele rondgang verbreid, in een kringloop gedreven, en zo verhindert ze dat door beviezing het buitenste gedeelte van de druppel vast wordt. |
[ 475 ]
|
Maar de cilinders kunnen toch niet geheel vloeibaar zijn, en daarna van binnen bevriezen, omdat ze in ronde druppels zouden overgaan zolang ze vloeibaar zijn. Dus bestaan ze in het begin veeleer geheel uit ijs, en daarna smelt het buitenste. Doch wat dan is gesmolten, kan niet gemakkelijk opnieuw bevriezen wegens de warmte van de kegel BAC, die zich bij de gehele rondgang verspreidt°). *) Ed. 1644. Over de vorming van een druppel, met o. a.:
In de vertaling van Glazemaker (1659), 237:
Huygens aanvaardt hier kennelijk het idee van de in de druppels ronddraaiende subtiele materie.
[ *) Iets dergelijks is genoteerd door Isaac Beeckman, Journal, II, 5.] |
[ 476 ]
Aanhangsel IXVan de hele was de vorm en grootte aldus: Verder waren ze heel vlak en heel dun, en naar het midden toe niet steviger dan elders; en door de warmte gesmolten maakten ze een heel klein waterdruppeltje zoals een raapzaadje. 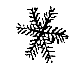 De vezeltjes van de blaadjes waren zo geplaatst als ze in deze grotere figuur zijn weergegeven, te weten dat ze elk afzonderlijk evenwijdig waren met de naburige stralen; wat heel duidelijk te zien was met een microscoop. De stralen waren bij sommige van ongelijke lengte, maar de hoeken bij het middelpunt waren alle precies 60°. [<]
De vezeltjes van de blaadjes waren zo geplaatst als ze in deze grotere figuur zijn weergegeven, te weten dat ze elk afzonderlijk evenwijdig waren met de naburige stralen; wat heel duidelijk te zien was met een microscoop. De stralen waren bij sommige van ongelijke lengte, maar de hoeken bij het middelpunt waren alle precies 60°. [<]
Erasmus Bartholinus heeft ook andere dergelijke vormen waargenomen, in zijn dissertatie over de vorm van sneeuw, gedrukt in 1661*).
|
[ 477 ]
| Nadat ik er verscheidene uitgehaald had, heb ik gevonden dat ze op dezelfde manier gebouwd waren als de blaadjes van zeshoekige sneeuw die ik vaker had waargenomen. Want ze hadden stralen zoals die, waarbij uit elk afzonderlijk aan weerskanten vele andere uitstaken, schuin onder een hoek van 60°, en als ze aan de randen gesmolten waren, waren er puntjes te onderscheiden, op een rij en op gelijke afstanden. |

|
§ 3. 16 jan. 1665. Urine vanmorgen bevroren gevonden, en op het oppervlak twee volmaakte sterren met zes stralen, met volstrekt gelijke hoeken bij het middelpunt; naast een aantal onvolmaakte, en blaadjes zoals in de voorgaande waarneming.
 *) Deze alinea is kennelijk later toegevoegd. Het gaat om: "Erasmi Bartholini D. & P. P. De figura nivis dissertatio, Hafniae, Typis Matthiae Godicchii, Sumptibus P. Hauboldi, Anno MDCLXI" [T. p.]. Huygens kopieert hier verscheidene figuren eruit. [Zie 'Sneewfiguren'.]
*) Deze alinea is kennelijk later toegevoegd. Het gaat om: "Erasmi Bartholini D. & P. P. De figura nivis dissertatio, Hafniae, Typis Matthiae Godicchii, Sumptibus P. Hauboldi, Anno MDCLXI" [T. p.]. Huygens kopieert hier verscheidene figuren eruit. [Zie 'Sneewfiguren'.] °) Huygens schijnt het verschijnsel van onderkoelde vloeistof niet gekend te hebben, aangezien hij het plotseling bevriezen toeschrijft aan de werking van warmte. Vergelijk de noot °) op p. 475.
|
[ 478 ]
Aanhangsel XWitte cirkel
|
[ 479 ]
|
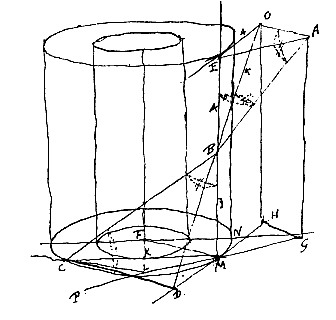
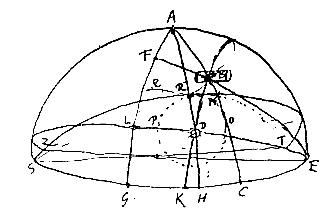
Evenzo is zijde MF gelijk aan zijde GN, omdat de hoeken FEM en GEN gelijk zijn. Dus zal ook de resterende zijde FO gelijk zijn aan de resterende zijde GP. En daarom is ook hoek FEO gelijk aan hoek GEP. En omdat de complementen hiervan tot een rechte hoek de hellingshoeken zijn met de horizon van de stralen FE en EG, zullen ook die hellingshoeken met de horizon gelijke hoeken zijn. Wat te bewijzen was. Het bewijs is hetzelfde wanneer de straal FE binnen de cilinder is, en door het oppervlak ervan teruggekaatst wordt, wat betrekking heeft op de bijzonnen om aan te tonen dat die in de witte cirkel gezien moeten worden [<]. Nevenzonnen
[ *) Figuur 14 van Tab. V uit "Opuscula Postuma" en formule van C. Visser (add. p. 550).] |
[ 480 ]
|
Om te vinden de hoek van de vertikale cirkels door de Zon en door één van beide bijzonnen naast de Zon [<]. De zonshoogte zij 10°. |
9.2396702 log. sinus van de |
[ 481 ]
9.9963018 log. sin. van compl. van vorige hoek. 9.9933515 log. sin. van compl. van |

[ 482 ]
|
§ 3. / MCB wordt verondersteld, daarmee worden gevonden / BAE, de hoogte van de |
[ 483 ]
Voorbeeld. / MCB 12°
9.9375306 sin. c. / MCD steeds gelijk, want afhankelijk van de dikte-
verhouding van ijs- en watercilinder. Hier wordt steeds 30° genomen
9.9904044 sin. c. / MCB
———————————
1|9.9279350 sin. c. 32.6 / BCD. diens sin. .53139
4
———————
2.12556
3
———————
.70852 sin. 45.7. / BAO.
|
[ 484 ]
9.3178798 sin. / BCM
9.7254203 sin. / BCD
-) —————————
9.5924586 sin. / DBM of EBO 66.58'.
9.5924586 sin. c. / EBO
9.8503675 sin. / BAO
———————————
1|9.4428261 sin. / BAE 16.6' hoogte van de
|
|
Gezocht wordt de hoek van de vertikale cirkels die door de |
zoals 1000 tot 680. sin. 42.49' |
[ 485 ]
Achterste bijzonnen |
[ 486 ]
|
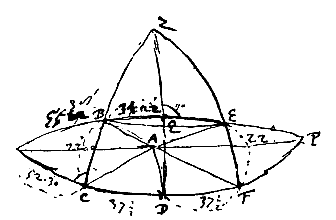
ZBC en ZEF zijn vertikale cirkels die door de bijzonnen gaan. Dit zijn de bijzonnen die gezien worden in het deel van de hemel tegenover de Zon. Wanneer hoek BAC, dat is de hoogte van de ware Zon boven de horizon, 22° is vind ik voor de hoek DAC of DAF 37½°. Dan zal de afstand van de bijzonnen zijn 68°44'.
Wanneer hoek BAC 18° is, vind ik voor DAC 40.0'. Met de cilinder vol water [<] heb ik deze hoeken onderzocht: |
10°30 41.30 25.30 35.0
18.0 40. 26.45 34.15
/ BAC 22. / DAC 37.30 / BAC 27.15 / DAC 34.0
22°30 36.15 27.30 33.30
24.15 35.30 28.30 32.30
/ BAC 30.45 / DAC 31.30
31.30 32.0
33.30 28.0
34. 27.15
35. 26.30
36. 25.
36.30 24.15
44.0 18.0
|
|
Als de Zon hoger is dan ongeveer 58 graden zullen de twee zonnen tegenover de Zon niet kunnen verschijnen. |
[ 487 ]
|
[...]*)
[ *) Figuur 19 van p. 415 en formule van C. Visser (add. p. 550).] |
[ 488 ]
|
Om te vinden de hoek van de vertikale cirkels door de Zon en door één van beide bijzonnen tegenover de Zon.
Stel de |
0.1290487 log. van de breking bij deze
|
[ 489 ]
9.8690152 log. sin. c. van vorige hoek.
0.3010300 log. 2.
+) ——————————
10.1700452
.2385606 log. \/3 of 1/2 log. 3. korter: tel op
-) —————————— log. 2 - log. \/3
9.9314846 sin. .... dat is 0,0624694.
0.1290487 log. van breking.
-) ——————————
9.8024359 sin. 29.23
2
—————
78.46
58.39
-) —————
20. 7
2
—————
40.14 gezochte hoek.
|
| Dit is de regel om de diameter van de Regenboog te vinden uit de gegeven brekingsverhouding, maar met gebruik van logaritmen. |
[ 490 ]
Omgekeerde bogen |
90. 0
HR in bijzonnen Rome 1630 [<] is 76.10
—————— (-
RA 13.50'
DR. 47.40'
DH. 28.30'
/ RAN = arc. HC. 48.16' op de gevonden manier.
|
| Om te onderzoeken of in het bijzonnen-verschijnsel te Rome van 1630, een bepaalde boog HRC (in de figuur van het verschijnsel [<]), hier QRB, in omgekeerde stand de kring PRO moest raken. Gezocht wordt een of ander punt op de boog QRB. |
[ 491 ]

/ MCB. 12.0'.
MCD. 44.
9.8569341 sin. c. MCD steeds dezelfde.
9.9904044 sin. c. MCB.
———————————
1|9.8473385 si. c. 45°17' BCD. diens sinus 71059
4
———————
2.84216
3
———————
94739 sin. 71.20' BAO.
|
[ 492 ]
1|9.3178789 s. BCM.
9.8516220 s. BCD;
———————————
sin. c. 9.4662569. 72.59 DBM, EBO.
9.9765318 sin. BAO.
———————————
1|9.4427887 sin. 16.6'. BAE
|
[ 493 ]

BD, LF. 53.4'
90.0 1|9.4429728 sin. 16°6' DL = BF.
hoogte van
|
[ 494 ]
1|9.3913595 t. AR. 20.18' AN 9.8232554 s. c. RAN. 17.35' AB ——————————— —————————— 9.5681041 t. AN. 2.43' BN. |
|
Gezocht wordt een ander punt op de boog QRB .... / MCB [Fig. 56] 6.0' .... HC. 24.35' .... BN. 0.36'.
|
[ 495 ]
|
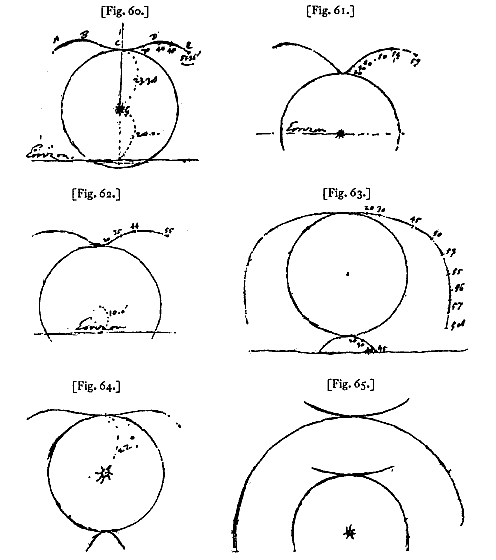
het is zeer wel mogelijk dat hij zich inderdaad bediend heeft van dit systeem om bij benadering een aantal punten te bepalen van de omgekeerde bogen, voldoende om hun vorm vast te stellen bij verschillende zonshoogten. Hij zegt bij een berekening: Deze boog DB wordt gevonden uit de bekende boog DL: en hij wordt niet door berekening gevonden maar door middel van de kromme lijn die beschreven wordt met behulp van de tabel die aan het begin van deze pagina staat. Hier is deze tabel voor een zonshoogte van 10°: Hoogte van dewaarbij Huygens in de marge noteert:
Als bij de figuur van deze pagina of die van pag. 11 [Fig. 59] deze getallen gevoegd worden, betekent de
De getallen die bij de kromme bogen zijn geschreven staan voor het aantal graden van de zonshoogte boven de bases van de cilinders, die op deze plaatsen de bogen laten zien. Maar wanneer die hoogte groter is dan 35 of misschien 40 graden wordt het licht te zwak om de bogen te maken, en daarom denk ik dat bijna nooit de buitenste delen van deze bogen onderscheiden worden, zeker voorbij het getal 40. Hier ook {Fig. 61] zoals in de vorige, wordt de ijscilinder in diameter de helft gesteld ten opzichte van de watercilinder. Maar de Zon staat op de horizon.
Bij zonshoogte 10° [Fig. 62]. Bij zonshoogte 30° [Fig. 63]. *) 23° 38' geldt voor: ijskern in diameter de helft van de hele cilinder, en brekingsindex van water 4/3. |
[ 496 ]
|
[ Vgl. III, 316, brief aan Hevelius, 22 aug. 1661. Simulatie: 'Tangent arcs'.] |