Regenboog
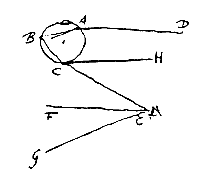 Laat dan ABC een regendruppel voorstellen, en DA een straal van de Zon die daarop schijnt. Deze wordt van A naar B gebroken, en van B teruggekaatst naar C, met AB en BC noodzakelijk gelijk; en laat hij, in C wederom gebroken, vandaar naar het oog E gericht zijn. Trek CH en EF evenwijdig met de zonnestraal DA, en de hoek FEG is gelijk aan CEF.
Laat dan ABC een regendruppel voorstellen, en DA een straal van de Zon die daarop schijnt. Deze wordt van A naar B gebroken, en van B teruggekaatst naar C, met AB en BC noodzakelijk gelijk; en laat hij, in C wederom gebroken, vandaar naar het oog E gericht zijn. Trek CH en EF evenwijdig met de zonnestraal DA, en de hoek FEG is gelijk aan CEF. De hoek HCE nu kan van verschillende grootte wezen, naargelang men de straal DA op verschillende plaatsen van de druppel ABC doet vallen, maar kan nooit groter wezen dan 41° 30', zoals uit Descartes' tabellen te zien is; zodat dan ook de hoek CEF en FEG niet groter kan wezen dan 41° 30'. Hierdoor komt het dat geen van de druppels die buiten de kegel CEG gevonden worden, deze gebroken zonnestralen naar het oog E kunnen zenden, maar alleen die daar binnen zijn. Doch díe zenden de meeste, die het dichtst bij het kegeloppervlak CEG komen. En daarom is de afscheiding van deze lichte druppels en de donkere buiten de kegel des te beter kenbaar, en die maakt zo dat hier een ronde ring verschijnt, die geheel zou verschijnen indien het aardoppervlak niet in de weg was — want nu kan het hoogstens maar een halve cirkel worden als de Zon maar even boven de horizon staat.
Dit is de ware oorzaak van de regenboog, en dat die met de ondervinding overeenkomt kan ook iedereen zien als hij een glazen bol, met regenwater gevuld, op zodanige positie t.o.v oog en Zon opstelt als hier de bol ABC is.
Als men dan nu het rond ABC bedenkt te zijn de horizontale doorsnede van een rechtopstaande cilinder (waarvan men zich een grote menigte dicht bij de horizon moet voorstellen). en dat de straal van de Zon (welke ik eerst zal nemen maar net aan de horizon te zijn), daar ook met de zelfde brekingen door gaat als de straal DABCE door de ronde druppel (eveneens met hoek HCE of CEF hoogstens 41° 30'), dan volgt evenzo dat geen cilinders buiten de hoek CEG staand, de gebroken straal naar het oog E kunnen zenden, en dat die net daar binnen staan de meeste stralen daar naar toe werpen,
 zeg ik dat deze 2 bijzonnen in de zelfde witte ring moeten staan waarin de andere staan, naar we aangetoond hebben [
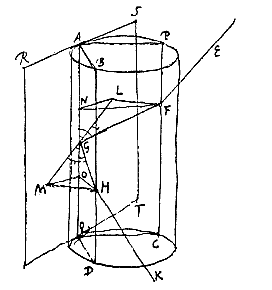
zeg ik dat deze 2 bijzonnen in de zelfde witte ring moeten staan waarin de andere staan, naar we aangetoond hebben [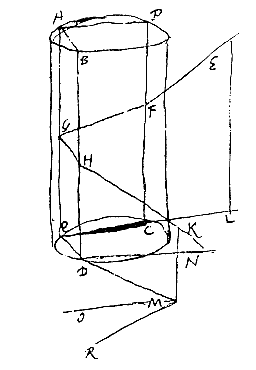 dat de straal FG, teruggekaatst in GH, wegens de terugkaatsingswetten gelijke hoeken maakt binnen op het cilinderoppervlak, en zó gaat, dat als door FG en GH vlakken worden getrokken evenwijdig met de cilinderas, hun snijdingen met het cilinderoppervlak de rechthoeken PAQC en ABDQ maken, met gelijke hoogte en breedte; en dat de stralen FG en GH de zijden van deze rechthoeken ontmoeten onder gelijke hoeken. Dit kan wel gemakkelijk bewezen worden, maar voor wie het aandachtig beschouwt is het vanzelf duidelijk genoeg.
dat de straal FG, teruggekaatst in GH, wegens de terugkaatsingswetten gelijke hoeken maakt binnen op het cilinderoppervlak, en zó gaat, dat als door FG en GH vlakken worden getrokken evenwijdig met de cilinderas, hun snijdingen met het cilinderoppervlak de rechthoeken PAQC en ABDQ maken, met gelijke hoogte en breedte; en dat de stralen FG en GH de zijden van deze rechthoeken ontmoeten onder gelijke hoeken. Dit kan wel gemakkelijk bewezen worden, maar voor wie het aandachtig beschouwt is het vanzelf duidelijk genoeg.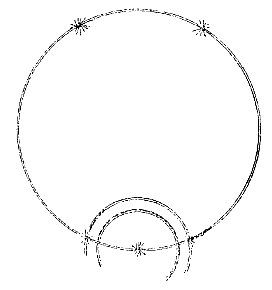 Maar volgens het schema van Scheiner zoals het in Gassendi's boek staat [
Maar volgens het schema van Scheiner zoals het in Gassendi's boek staat [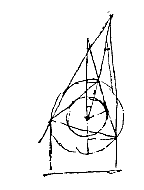 Daarom, in het 'phaenomenon romanum' [1630], waarbij de Zon nog hoger was (te weten 28°), als alleen de cilinders die de bijzonnen O en P maakten omtrent de achterste delen van de witte ring gevonden werden, terwijl de andere cilinders van de bijzonnen M en N naast de Zon niet zo ver strekten, dan kunnen er geenszins bijzonnen in dat achterste deel van de witte ring geweest zijn. Want in die cilinders heeft de kern tot de hele cilinder de verhouding van ongeveer 624 tot 1000.
Daarom, in het 'phaenomenon romanum' [1630], waarbij de Zon nog hoger was (te weten 28°), als alleen de cilinders die de bijzonnen O en P maakten omtrent de achterste delen van de witte ring gevonden werden, terwijl de andere cilinders van de bijzonnen M en N naast de Zon niet zo ver strekten, dan kunnen er geenszins bijzonnen in dat achterste deel van de witte ring geweest zijn. Want in die cilinders heeft de kern tot de hele cilinder de verhouding van ongeveer 624 tot 1000.