OC

[ Halo's en bijzonnen werden in de 17e eeuw nog algemeen beschouwd als wonderbaarlijk voorteken van wat iemand maar kon verzinnen. Evenals Descartes zag Christiaan Huygens in deze verschijnselen een uitdaging voor het redelijk denken. Nadat hij in 1652 een aantekening gemaakt had van een kring om de Zon ging hij Descartes' Météores*) bestuderen, en waarnemingen verzamelen. In 1658 had hij een lijst met vragen, en een verklaringsprincipe (>).   In de periode 1658 - 1663 schreef Huygens de verhandeling 'De Coronis et Parheliis' (over halo's en bijzonnen). Een gedrukte versie verscheen pas in 1703, in het Latijn in de Opuscula Postuma. Hoewel niet alle verklaringen juist zijn°) is er een aanmerkelijke vooruitgang ten opzichte van Descartes. En wat 'voortekenen' betreft: "omina vana", ze zijn uit de lucht gegrepen (>).]   *)  1637; inhoudsopgave: table, regenboog: 250- (fig.). In 1659 verscheen een vertaling van J. H. Glazemaker: Verhevelingen (regenboog: p. 276).   °)  Zie Halo's (Kees Floor), Alte Halo-Darstellungen (meteoros.de), Sun Dogs (Hyperphysics).   N.B. Een ander verschijnsel is de 'corona' (diameter tot 15°), ontstaan door diffractie, blauwachtig aan de binnenkant, zie 'colours' (Atmospherc Optics). Uit Voorbericht (351-362):

[ 355 ]

Halo. 30 Mei 1652.  Ik heb een cirkel in de lucht rondom de zon waargenomen. De zon stond in het middelpunt. De middellijn van de cirkel was ongeveer 46 graden; en de breedte zoals die van de gewone regenboog. Maar ook de kleuren waren zoals in de regenboog, maar zeer zwak zodat ze nauwelijks te zien waren, en in tegengestelde stand zodat het rood het dichtst bij de zon was. Het blauw was zeer witachtig. De gehele ruimte binnen de cirkel werd ingenomen door een donkerder damp dan de overige lucht; waarvan de toestand zodanig was dat ze als door een aaneensluitende dunne wolk de hemel dof maakte, terwijl de bovenlucht er toch doorheen scheen. De wind blies uit het noorden, maar zeer kalm. De verklaring hiervan die Descartes in Meteores geeft [fig.] voldoet niet, ten eerste omdat niet blijkt waarom niet alle platte stukjes ijs die hij noemt de zonnestralen zouden doorlaten, zelfs niet die binnen de cirkel zijn; ten tweede wegens de dunheid van de wolken die veeleer lijken te bestaan uit mist dan uit hagel.

[ 365 ]

Waarnemingen   § 1.  Alhoewel de oorzaken van de kringen [halo's] en van de bijzonnen die wij zullen aangeven niet veel van elkaar verschillen, zal ik nochtans eerst over die van de kringen handelen, omdat de uitleg ervan gemakkelijker is, en (als hij begrepen is) ook die van de bijzonnen begrijpelijker maakt.

[ Marge: ]

Eerst geheel betrouwbare waarnemingen. Dan beginnen met wat voor alle gemeenschappelijk is. Dan wat bijzonder is voor elk apart. Daarna minder nauwkeurige en twijfelachtige waarnemingen.

De kringen dan zijn ronde ringen, die soms overdag om de Zon en bij nacht om de Maan gezien worden, nu eens wit, dan weer (als ze zich sterker vertonen) ook met kleuren versierd zoals de regenboog. Ze zijn gewoonlijk ongeveer 45° in diameter, maar soms worden er ook grotere waargenomen die een diameter van 90° hebben, of nog meer. En er wordt gesproken van 3 en meer tegelijk die alle de Zon als middelpunt hadden. Ik heb die van 45° dikwijls waargenomen, maar de eerste keer het duidelijkst, waarvan ik ook aantekende wat daarbij opmerkelijk was — en dat nog voordat ik ooit naar de verklaring gezocht had van zulke verschijnselen. Ik noteerde dan dat deze ring gekleurd was, maar flets in vergelijking met een mooie regenboog. En dat de rode kleur aan de binnenkant stond, en de blauwe buiten, en deze was heel witachtig. Verder dat de hele ruimte binnen de ring (en hierom zijn dit misschien 'gebieden' genoemd) duisterder scheen dan de andere lucht daar buiten, die bijna geheel helder was, en alleen met dunne doorzichtige witte wolkjes betrokken. Tenslotte bevond ik dat de diameter van de ring ongeveer 45° was, alhoewel ik die maar ruwweg afmat met een stokje, dat ik zo ver voor me hield als mijn arm kon reiken. Ik bepaalde welk gedeelte daarvan de breedte van de ring innam, en daaruit kon ik daarna de hoek bij benadering berekenen. Deze waarneming heeft de dagtekening 30 mei 1652.

[ 367 ]

Verklaring Ik herinner me dat ik, na deze waarneming gedaan te hebben, opzocht wat Descartes over de oorzaak van dergelijke kringen schrijft, te weten dat die voortkomen uit de zonnestralen als deze gebroken zijn in zekere platachtige sterretjes van ijs. En dat ik daarover niet voldaan was, omdat daar uit volgen moest (zoals hij ook zelf zegt) dat de ruimte door de ring omsloten, helderder zou moeten zijn dan de lucht daar buiten, wat ik andersom bevonden had.   § 2.  Ik dacht daarna dat men een andere reden van dit hemelverschijnsel moest zoeken, al zegt dezelfde auteur dat wij geen andere oorzaak in de wolken kunnen vinden die zo iets zou voortbrengen. Ik ging alle terugkaatsingen en brekingen na die de stralen van de in waterdruppeltjes kunnen ondergaan, doch vond niet dat daar op de een of andere manier een ring van deze afmeting uit kan ontstaan. Ik nam ook de vrijheid om enige andere vormen van ijs-druppels willekeurig te verzinnen, maar alles tevergeefs. Zo moeilijk is het een afbeelding te verzinnen van iets dat nooit gezien is. Maar toen ik na verloop van 6 jaren weer die zelfde gedachten begon te hervatten naar aanleiding van een verschijnsel van 5 zonnen, te Warschau gezien in 1658 [>], en toen ik goed ging letten op de gedaante van de genoemde kring, is mij eindelijk de ware oorzaak ingevallen. En kort daarna ook die van de bijzonnen, waarvan ik overal waarnemingen was gaan verzamelen. Want ik aarzel niet die oorzaken de ware te noemen die zo goed met het waargenomene overeenkomen dat ik verloren moeite schijn te doen als ik nog andere zoek. Toen bedacht ik dat bepaalde kleine deeltjes, in de wolken zwevend, de materie moesten verschaffen voor deze hemelverschijnselen — want dat bleek wel uit het feit dat bij het wegdrijven van de wolken de ring nochtans op dezelfde plaats was blijven staan — en dat de duisterheid van het ronde gebied in de ring een aanwijzing was dat die deeltjes daar de zonnestralen niet zo goed laten passeren als wanneer ze buiten die hoek weggedreven zijn. En zo kwam het snel bij me op dat dit kon gebeuren indien elk van deze deeltjes een ronde korrel was van helder ijs of wel met water er omheen, en met een minder doorzichtig korreltje er binnenin. Want bij een grote menigte van zulke deeltjes, alle op dezelfde manier gemaakt, tussen ons oog en de Zon zwevend, begreep ik gemakkelijk dat die daarvan, die binnen een zekere hoek van de afstonden, geen van zijn stralen naar ons oog lieten komen; maar wel de andere, buiten deze hoek gelegen; zoals aanstonds bewezen zal worden.

[ 369 ]

Dat er nu zulke hagel-druppels werkelijk in de wolken gevonden worden is niet alleen waarschijnlijk maar volkomen zeker omdat die soms op de grond neervallen, zoals Descartes getuigt in Météores. Want daar, als hij over hun ontstaan spreekt, zegt hij [219]: .... D'où vient que le dehors de chasque grain de cette gresle, estant ordinairement composé d'une glace continuë & transparente, il y a dans le milieu un peu de neige, ainsi que vous pourrés voir en les cassant. [ Glazemaker, 249: ... En hier uit koomt'et dat, dewijl het buitenste van yder korreltje van deze hagel gemenelijk uit een eenparig en deurschijnig ys bestaat, in 't midden een weinig sneeu is, gelijk men zien kan, als men hen breekt.] En niemand hoeft zich erover te verwonderen hoe de sneeuwbolletjes midden in 't water blijven zitten. Want men moet bedenken — omdat de hele druppels door de dampen (die van beneden komen) omhoog gehouden worden — dat het water niet de neiging heeft er af te vallen en de middelste kernen te verlaten. En deze, met dezelfde dichtheid als water, hebben ook geen reden om van het middelpunt der druppels opwaarts of neerwaarts te zakken. En dat dit althans zo is tonen die ijskorrels duidelijk die op de grond terecht gekomen zijn. Maar de hele druppels moeten mijns inziens zeer klein zijn, zoals raapzaad misschien of noch kleiner, om door de dampen omhoog gehouden te kunnen worden. Welke kleinheid nochtans niet de volmaaktheid belet van de vorm, noch van de verhouding tussen de dikte van de hele druppels tot die van de middelste kern. Deze verhouding zal ik ook onderzoeken. Nu we dan gezien hebben dat er zulke gemengde deeltjes in de lucht voortgebracht worden, wil ik tonen hoe deze de verschijning van de kring veroorzaken. Druppel   § 3.  Daartoe zullen we één van deze druppels in 't groot laten zien om de breking van de zonnestralen daarin te kunnen aanwijzen. Deze druppel zij dan ABCD, met een korrel van sneeuw EF in het midden.   Stellen we nu dat de stralen van de Zon van de kant GH invallen, dan weten we dat die eerst aan het oppervlak AD worden gebroken, en van daar binnenwaarts gebogen, waardoor noodzakelijk moet gebeuren dat een groot deel ervan komt te stuiten tegen de sneeuwkorrel EF.

[ 371 ]

Doch laat het de stralen GA en HD zijn waarvan de gebroken stralen AB en DC juist passeren langs de genoemde korrel EF. Deze dan worden in B en C nog eens gebroken, en lopen dan naar elkaar toe, elkaar snijdend in K, welk punt wat minder dan een halve diameter lengte van de druppel ABCD af staat, zoals in de 'Dioptrica' (Prop. 13) is aangetoond. Als nu BK en CK verlengd zijn naar M en L dan volgt dat op welke plaats binnen de hoek, of om precies te zeggen, binnen de kegel LKM het oog ook opgesteld wordt, dit geen helderheid van de Zon door bol ABCD kan waarnemen, omdat alle stralen die naast de korrel EF passeren, elkaar onder een grotere hoek snijden en dichter bij de bol ABCD, zodat ze buiten de kegel LKM vallen (zoals ook in 'Dioptrica' bewezen wordt). Maar als het oog buiten deze kegel is opgesteld, zoals in O of P of waar 't zou mogen zijn, beneden de druppel, dan komen daar stralen van de Zon en die maken dat men zijn schijnsel in de druppel gewaarwordt.   Zoals het nu in deze druppel gebeurt, evenzo is het met alle die van 't zelfde maaksel zijn, te weten dat elk ervan afzonderlijk zo'n schaduwkegel achter zich heeft waarbinnen men geen stralen van de Zon kan zien (ik heb het over stralen die door de druppel heen gaan), maar als men net daarbuiten is krijgt men altijd zulke stralen in 't oog. Genomen nu dat het oog in N is, en dat men zich een kegel voorstelt waarvan de top N is en met de zijden NR en NQ parallel met de zijden KL en KM van de kegel LKM: het is zeker dat geen druppels met korrels, zoals ABCD, die binnen de gehele kegel QNR gevonden worden, de zonnestralen naar het oog N kunnen richten. Want als men uit één van deze druppels, zoals S, twee lijnen trekt evenwijdig met KL en KM, zoals SV en ST — die in dit vlak voorstellen de zijden van de schaduwkegel achter de druppel S — dan blijkt dat het oog N (oftewel de top van de kegel QNR) binnen de genoemde kegel VST valt, en dientengevolge geen stralen van de Zon ontvangt die door de druppel S gaan. En evenzo is het met alle druppels binnen de kegel QNR, want het oog N staat binnen elk van hun kegels, zoals uit deze figuur duidelijk is.   § 4.  Maar indien men een of andere druppel beschouwt die buiten de kegel QNR is, zoals X, en zijn kegel YXZ, dan is het klaar en duidelijk dat het oog N daar buiten valt, en daarom zullen er stralen van de Zon die door de druppel X komen daarop stralen, zo dat die druppel verlicht zal schijnen,

[ 373 ]

en evenzo alle andere buiten de kegel QNR, terwijl die daar binnen zijn veel duisterder zullen zijn omdat ze geen beeld van de Zon hebben. Daarom blijkt hieruit dat een rond gebied om de Zon zich donker moet vertonen, maar wat buiten de omtrek van het gebied is geeft meer licht; en wel het meest de naaste omgeving ervan, omdat de druppels die het dichtstbij aan de buitenkant van de kegel QNR liggen, het grootste beeld van de Zon leveren (zoals gemakkelijk te bewijzen zou zijn). Het blijkt ook dat bij elke zonshoogte op dezelfde wijze een kring voortgebracht kan worden, en wel wegens de bolvorm van zowel de hele druppels als de kernen in hun binnenste. Experiment En wie zich ook met een proef dit verschijnsel wil voorstellen, die moet een bol nemen van dun glas, en deze met water vullen en daar middenin een bol opstellen die niet doorzichtig is (waartoe wel een middel is te vinden). Men zal bevinden, als men die naar de Zon toe keert, dat men daarin geen schijnsel van de Zon zal zien, behalve als men hem een stuk weegs buiten de lijn gehaald heeft die van het oog naar de Zon strekt; en als men gekomen is juist waar men de Zon erdoor kan zien, dat zijn beeld daar het allerhelderst is. En men zal ook hier de rode kleur gewaarworden, die hier om dezelde reden gezien moet worden als in een prisma van kristalglas, of liever van water indien men er zo een kon maken, want de straal GA bij voorbeeld ondergaat juist dezelfde breking bij 't inkomen van de druppel in A en bij 't uitkomen in B, als wanneer hij zou gaan door het prisma AΩB, waarvan de zijden AΩ en BΩ de druppel raken in A en B. En de korrel EF die het licht aan de ene zijde begrenst, draagt mede bij tot het kleuren van de stralen zoals AB die daar het dichtst langs heen gaan. Doch de reden voor deze kleuren verder te onderzoeken, te weten waarom die in een prisma voortgebracht worden, dat wil ik geenszins ondernemen, ja zelfs beken ik dat ik de reden ervan volstrekt niet weet, en ik denk niet dat iemand ze gemakkelijk zal doorgronden zo lang er niet meer licht geworpen zal worden op de wetenschap der natuurlijke dingen. Alleen wil ik dat men erop let dat de rode kleur die in deze bol gezien wordt, ook gezien moet worden in de genoemde druppels die juist buiten de kegel QNR liggen; en doordat hij afneemt in de verder afgelegen druppels brengt hij ook de andere voort, zoals ook in de regenboog gebeurt. En zo ver als deze kleuren zich uitstrekken — omdat hier tegelijk ook de meest verlichte druppels zijn — zo breed wordt de ring of kring geacht te zijn, overigens in werkelijkheid alleen aan de binnenkant naar de Zon toe begrensd, en niet aan de buitenkant. Wat ook evenzo in de regenboog gebeurt, want die is eveneens (zoals uit Descartes' uitleg blijkt) alleen aan de zijde van de rode kleur begrensd.

[ 375 ]

Deze kringen worden ook om de Maan dikwijls gezien, juist om dezelfde reden als om de Zon, doch vaak zijn die zo weinig gekleurd dat ze alleen wit schijnen, zoals ik eveneens dikwijls in die om de Zon waargenomen heb wanneer ook nauwelijks het donkerder gebied binnen de cirkel onderscheiden wordt van het overige dat helderder is.

[ Marge: ]

Dit gebeurt doordat zulke korrels zo weinig materie hebben, want hoe meer hiervan er is hoe mooier de kringen lijken, zoals te zien is aan de waarneming van Golius, hierna, en die van Lesna [>], want men ziet daar duidelijk dat waar het gebied binnen de kring het donkerste is, d.w.z. waar de zwerm van korrels het dichtst is, dat daarnaast de kring ook het mooist gekleurd is.

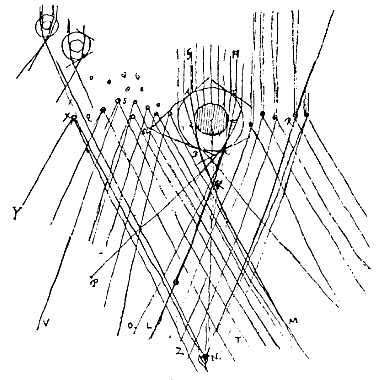
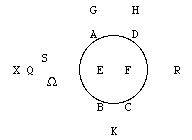
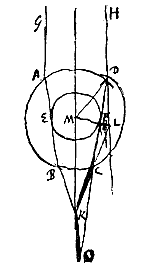Maar nog door een andere oorzaak worden wel de schoonste kleuren, en de levendigste, gezien in de kringen die tegelijk met bijzonnen of bijmanen verschijnen, waarvan ik de reden zal zeggen wanneer ik daar aan toekom [>]. Middellijn   § 5.  Laten we nu verder bezien de grootte van de middellijn van de kring, waarvan we zeiden dat hij meestal 45° is [<]. Het is wel duidelijk dat deze afhangt van de grootte van het ondoorzichtige korreltje EF. Want hoe grooter het is in verhouding tot de hele druppel AC, zo veel te groter zal ook zijn de hoek BKC, waaraan gelijk is de kegelhoek QNR die de middellijn van de kring bepaalt (zoals voldoende bewezen is). Ik zeg dan dat de middellijn van het ondoorzichtige korreltje &c. Want laat behalve de stralen HDCK en GABK die door de druppel ABCD gaan en de korrel aanraken in E en F, getrokken worden uit het middelpunt M de rechte lijn MKO die door hun snijpunt K gaat, en met de verlengde rechte DC in O samenkomt. Laat ook HD en KC, binnen de druppel verlengd, elkaar ontmoeten in L. Dan zijn in de driehoek DLC de hoeken D en C gelijk, doordat de straal HD bij 't inkomen van de druppel in D juist zo veel gebroken wordt als bij 't uitgaan in C. Aan hoek D is nu gelijk de hoek DOK, omdat HL en MO evenwijdig zijn. Bijgevolg zullen in ΔCKO ook gelijk zijn de hoeken O en C, en aan de som van deze twee is gelijk CKM, de helft van hoek CKB. Omdat dan de hoek BKC 45° moet zijn, zal zijn helft MKC zijn 221/2 gr. en de helft hiervan is hoek O van 11° 15'. Dus in ΔOMF die de rechte hoek F heeft is de verhouding van de zijden gegeven, en als OM als cirkelstraal genomen wordt van 100000 delen, zal MF (de sinus van 11° 15') zijn van 19509 delen, en OF van 98078. Gegeven nu is ook de verhouding van OM tot OD, die is degene die de brekingen van het water meet (zoals aangetoond in prop. 8. van de Dioptrica), te weten 187 tot 250.

[ 377 ]

Als dus OM gesteld wordt op 100000, zal OD 133690 zijn, en daarvan afgetrokken OF 98078 blijft over FD 35612. Maar MF was 19509. Dus, met de verhouding van deze zijden in de rechthoekige driehoek MFD bekend, zal ook gegeven worden de verhouding van elk van beide tot de zijde MD en deze zal bevonden worden van 40605 delen te zijn. Dus moet de halve midellijn van de druppel MD zich verhouden tot de halve diameter van de sneeuwkern MF als 40605 tot 19509, oftewel bij benadering als 1000 tot 480 opdat de middellijn van de kring 45° is. Op dezelfde manier zal men vinden dat om de middellijn van de kring van 90° te maken de verhouding van MD tot MF moet zijn als 1000 tot 680. Warmte   § 6.  Wat betreft het ontstaan van de natte hagel is te bedenken dat het eerst bolletjes van fijne sneeuw zijn, die door het vliegen door de lucht rondachtig worden. Deze worden door de warmte der Zon van buiten een stukweegs gesmolten. En dat de lucht een zekere getemperdheid tussen koude en warmte moet hebben als de kringen gezien worden, zodat de korrels maar net en langzaam komen te smelten. En als er dan weer iets meer kou over komt, smelten ze niet verder. 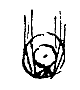Maar na het smelten tot op de helft van hun dikte of iets verder, belet de kegel van teruggekaatste stralen binnen de druppel door zijn warmte dat deze weer verder kan bevriezen, ook als hij in grotere koude komt. Door welke warmte — die het grootst is omtrent de punt van de genoemde kegel — ook de resterende sneeuwkern rond gemaakt wordt, omdat de druppel nu eens de ene en dan weer de andere zijde naar de Zon toe keert, ofwel omdat de warmte van die kegel zich overal in de druppel verspreidt [>]. Deze ronde vorm is voor het verschijnen van de kring vereist. Want het is duidelijk dat ook wel veel druppels verder of minder smelten, maar als de binnenkernen ervan niet rond gemaakt worden kunnen ze samen geen effect hebben. En misschien wordt door deze zelfde warmte de koude te meer in 't midden van de druppel geconcentreerd (zoals men dit op verschillende manieren 's winters ziet gebeuren) en wordt daardoor belet dat de kern ook gemakkelijk verder ontdooit [>]. Want men moet weten dat de geringste tegenstand van de ene en de andere kant, bij de genoemde getemperdheid van de lucht, genoeg is om deze druppels aldus half ontdooid te houden. Ik stel dat het buitenste deel van de bolletjes water is, omdat het wat waarschijnlijker is, want daardoor wordt het oppervlak effener en geschikter om zekere brekingen te maken, dan schijnt te kunnen als het van ijs is. Doch evenwel kan het ook wel soms gebeuren dat de korrels (gevormd zoals eerder gezegd is) komen te bevriezen, en misschien is dat bevroren water daar omheen nog helder genoeg en volmaakt van vorm om de kring te maken.

[ 379 ]

Behalve nu de concentratie van stralen die de druppels doet smelten tot zo ver als gezegd is, wordt nog een andere concentratie gevonden zoals in de genoemde druppel te zien is in ...., door welke de sneeuwkernen groter dan de voorgaande (naar verhouding van de hele druppel) behouden kunnen worden en rond gemaakt; en door deze druppels komt een tweede kring te verschijnen, met een middellijn ongeveer 2 maal zo groot als de eerste, die ook soms waargenomen is, zoals hierna gezien zal worden.   Deze concentratie van stralen schijnt de reden te zijn waarom de kringen meestal met zulke middellijnen gezien worden, maar ook waarom wel kringen van allerlei andere middellijnen gezien kunnen worden. Want men kan zich voorstellen dat de druppels in die matige koude zeer langzaam voortsmelten, en — als een groter of kleiner deel daarvan gesmolten is — lang genoeg in ongeveer dezelfde verhouding blijven, om een kring zonder merkbare verandering van middellijn gedurende enige uren te doen verschijnen. En hierdoor kan het gebeuren dat een zwerm druppels tot een zekere diepte gesmolten is en een andere van die wat hoger of lager vliegen weer op een andere diepte, en nog andere zwermen met een andere verhouding, en dat veel verschillende kringen zich gaan vertonen; zoals door sommigen verteld wordt dat ze er 6 tegelijk gezien hebben die de Zon als middelpunt hadden.

[ Marge: ]

Snellius in het boek over de Komeet van het jaar 1618.  [p. 33]

§ 7.  Tot dusver hebben we de kringen om de Zon onderzocht, en hierna zullen we handelen over de bijzonnen en bijmanen. Hierin zijn veel meer en wonderlijker dingen op te merken, zoals men al kan constateren als men alleen de figuren bekijkt die hierna zijn ingevoegd.   [ ... ]