DESCRIPTIO AUTOMATI PLANETARII. R  ERUM coelestium scientiam ante bis mille annos inchoatam, magnisque ingeniis excultam, nostra demum aetate absolutam, ut mihi videtur, perfectamque habemus;  Idque ita, ut centum circiter his proximis annis plus profectum sit quam reliquo omni tempore.   Quae enim antea in hac arte praecipua erant, loca stellarum definire tum fixarum tum errantium; anni ac mensium spatia dispescere, Eclipses praedicere, ea omnia non solum multò melius planiusque nunc facere didicimus; sed & quod majus est, ac praeclarius, ordinem, positum, proportionem & figuram orbium caelestium, quibus circa Solem Planetae ac Tellus ipsa circumfertur, summa certitudine comprehensa tenemus; stellas fixas innumeras, planetasque alios Telescopii observationibus perceptos priorum numero addidimus.   Quae omnia ante Copernici aevum, quaedam & in nostrum usque, profundis tenebris demersa latebant.   Itaque si quis cogitet quantarum in arte sua rerum cognitione veteres Astronomi caruerint; adeo ut nec partes Systematis singulas, nec formam totius habuerint perspectam; facile quoque intelliget fieri non potuisse, ut instar ejus aut imaginem aliquam arte effingerent.   Quare etsi plurimùm celebretur doctorum scriptis Archimedea sphaera*) ac Possidonii illa, cujus apud Ciceronem mentio facta [432] reperitur, certum tamen est, nullam iis nec archetypi caelestis similitudinem inesse potuisse, nec verorum motuum imitationem, etsi summo ingenio, industriaque fabricatas fuisse credibile sit.   Ex eo vero tempore, quo reformata restitutaque in melius fuit Astronomia, sicut facilius res eadem tentari potuit, ita a pluribus quoque susceptam effectamque scimus; quorum & Machinationes quasdam vidimus, vario artificio elaboratas. [cf. p. 172]   Nos vero ab his omnibus diversam viam secuti tale fabricari curavimus   [ *)  Vergelijk Aanhangsel II, p. 649 (Ned.). Bronnen ook bij Isack Beeckman, 1629v.]

[ 591 ]

[ v ]

Automaton [Automatum], in quo exiguo rotarum continenter euntium numero effecimus, ut in tabulae planae superficie Planetarum quinque primariorum corpora circa Solem, Lunae vero circa Terram, cursus suos absolverent, iisdem quibus in caelo temporibus, atque in iis orbibus excentricis, qui caelestium veram dimensionem positumque exprimerent; servata quoque in singulis motuum inaequalitate, qua celerius feruntur in partibus a Sole minus remotis: & annotata denique exigua illa declinatione qua ab Eclipticae sive orbitae Telluris plano evagantur.   Adeo ut praeter spectaculi elegantiam, etiam positus Planetarum non modo in praesens tempus sed & in futurum aut praeteritum, tanquam ex perpetua quadam ephemeride hinc discere liceat, nec non conjunctiones, oppositionesque omnium, cum ad Solem, tum inter se; idque tanto exactius, quanto ampliore forma opus effectum fuerit.   Quae inventio cum a multis expetita sit, qui vel cognoscere, vel imitari eam cuperent, hoc libro cujusmodi sit exponemus.   Incipiam vero a Machinae constructione exteriori, quae totum opus complectitur.   Itaque Octogonum est è ligno coagmentatum, bipedali diametro, profunditate pollicum sex.  Hoc ad parietem ita suspensum est, & cardinibus suis libratum, [433] qui in sinistro latere affixi sunt, ut cum libuerit converti machina possit, & aversa parte recludi, quo interiora conspiciantur.   Facie anteriori lamina ex aere aurata cernitur toti octogono praetensa ac Vitro speculari tecta, in qua Planetarum orbes secundum Copernici systema, sed Keplerianas proportiones descripti sunt, ac penitus excisi, adeo ut per rimas eas pinnulae exiguae commeent, quibus Planetarum globuli dimidiati supra laminam ac velut in superficie ejus volvantur, Saturno quinos, Jove quaternos, Tellure unicum comitem, quae Luna nostra est, secum ferente, qui nimirum comites iisdem orbiculis impositi sunt, quibus Planetarum ipsorum corpuscula.   Nam & caeteris planetis qui comites nullos habent, ejusmodi tamen orbiculos addidi, qui circumfusum aethera referrent, simulque planetas efficerent visibiliores.   Ac Planetae quidem primarii omnes {Vide Tab. 1. Fig. 1.}, ut sunt praeter jam dictos, Mars, Venus, Mercurius, ita continue motus suos circa Solem immobilem peragunt, ut non tantum periodica tempora, sed &

[ 593 ]

[ v ]

anomaliae leges exacte servent. [cf. p. 125]  Circa Terram vero Luna menstruas revolutiones conficit.  At in Saturni Jovisque comitibus idem perficere non licuit; cum ob machinae parvitatem, tum ne aequo longius labor excresceret.  Itaque hi uno tantum orbiculo affixi tenentur, cujus primarius Planeta centrum occupat.

[Tab. 1, fig. 1.] [IMSS]

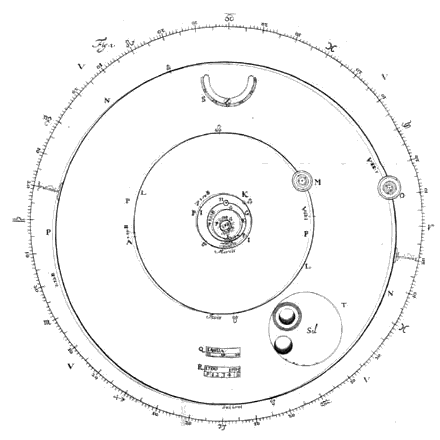
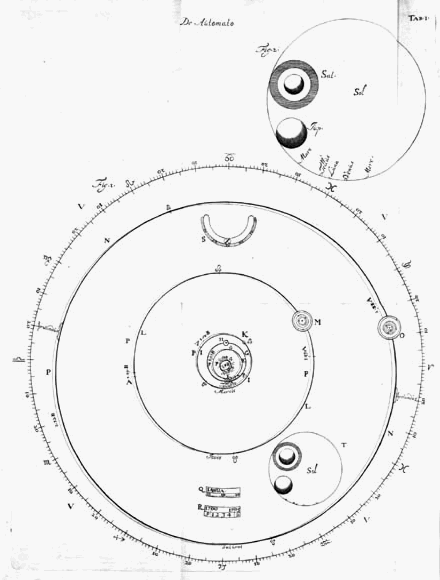
Porro omnes Orbitas Planetarias Eclipticae circulus amplectitur, signis suis duodecim, gradibusque 360 divisus.  In quo apparentia horum astrorum loca, facillime sic investigantur.  Nempe si locum Planetae secundum longitudinem, ut vocant, inquirere

[ 595 ]

[ v ]

placet, tantummodo filum è Tellure ad planetam illum extenditur; eique filo alterum ex Solis centro, quod ibi fixum [434] manet, Parallelum ducitur ad Eclipticae divisiones usque; hoc enim Planetae longitudinem ostendet.  Atque idem hoc parallelogrammo quodam filari ex bacillis duobus aequalibus duo fila itidem aequalia innexa habentibus constante peragi potest, clauso manente vitreo, quod supra indicavimus, operculo.  Huic enim parallelogrammum imponitur, atque oculo desuper manente immoto, ita coaptatur, ut altero filo super Terrae ac Planetae centrum transeunte, alterum Soli immineat, quod simul in Eclipticae circulo locum Planetae secundum longitudinem indicabit; de latitudine vero cognoscenda postea dicemus, postquam circulos in hunc usum describere docuerimus.

[ 597 ]

[ v ]

Inferiori parte Laminae, inter Saturni Jovisque orbitas foramina bina sunt parvo intervallo distantia, binosque pollices longa, dimidium lata, quorum superiore dies Mensis, altero Annus Epochae nostrae comparet, itidem ut caetera suis orbibus delati & Automati motu volubiles, quorum ille ter 8) 365 dierum aequales divisiones habet, hic trecentorum annorum. {Vide Tab. 3. Fig. 4.}   Motus autem ab incluso horologio oritur, quod idem horas quoque & scrupula prima indicat in semicirculari foramine inter Jovis ac Martis Orbes parte superiori inciso.  In eo namque numerus horae cujusque ordine praeterlabens, particulas quoque sexagesimas una opera demonstrat.    8)  De Volder et Fullenius ont à tort omis le mot "ter".

[Tab. 3, fig. 4.]  [>]

Movetur autem & manu machina tota, cum vel spectaculi gratia Planetarum discursus exigui temporis mora transigi placet, vel ad tempus datum futurum praeteritumve positus eorum requiritur.  Tunc enim lateri dextro Octogoni manubrium inseritur, quod levi manus motu conversum, qualibet circumductione annuum motum planetis universis superaddit; vel [435] contraria ratione agitatum tantundem illos in praecedentia retrahit, ut retrorsum quidem in centenos annos, in futurum ad ducenos, quaecunque fuit aut futura est coeli positura repraesentari queat.  Pari vero facilitate omnia rursus ad praesens tempus reducuntur, converso manubrio, donec ad puncta dictorum foraminum media dies annusque restituantur.  Quo peracto auferendum est manubrium, ut rursus automatico motu omnia sicuti prius ferantur.   Sed quae hactenus exposita sunt, quo clarius percipiantur figuram hanc Automati, quale extrinsecus apparet, adjicimus 9).

[ 599 ]

[ v ]

De Automato	Tab: 1
	[IMSS]

E X P L A N A T I O TAB.  1.   FIG.  1.   V.V. Ecliptica divisa in signa 12 & gradus 360.   B. Sol.   C. Orbita Mercurii.   D. Mercurius.   E. Orbita Veneris.   F. Venus.   G. Orbita telluris.   H. Tellus cum Luna, quae circa eam volvitur.   I. Orbita Martis.   K. Mars.   L. Orbita Jovis.   M. Jupiter cum quatuor satellitibus.   N. Orbita Saturni.

[ 601 ]

[ v ]

O. Saturnus cum quinque satellitibus.  A.A. Sunt loca Apogaei in singulis planetis. Denotant nodos in singulis planetis, illum ascendentem, hunc descendentem.  [436]  P.P. Sunt circuli latitudinum in singulis planetis.   Q. Notat anni mensem & mensis diem.   R. Notat annum Epochae Christianae.   S. Monstrat horas & horarum minuta.   T. Figura, quae denotat Planetarum ad Solem & inter se proportionem, quam Fig. 2. accurate exprimit.

Fig. 2.   Exhibet veram proprtionem magnitudinis disci Solaris, ad reliquorum
omnium Planetarum discos.

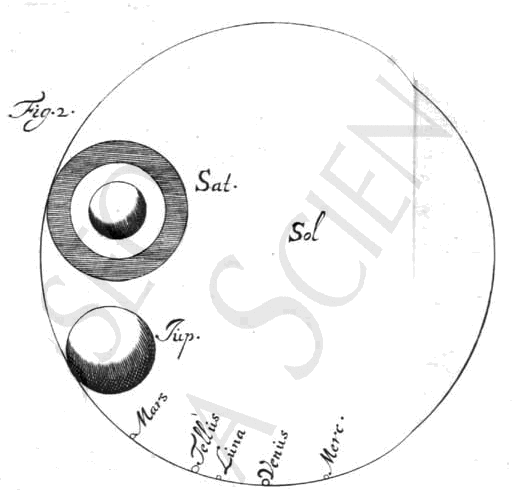
Caeterum fieri non poterat, ut ipsa Solis & Planetarum corpora suis proportionibus ad hunc orbitarum modulum exprimerentur; quippe quae omnia visu percipi ob exilitatem nequirent:*)  idcirco seorsim eos omnes in tabulae loco vacuo describendos curavimus ea, quae hic signata est, magnitudine.  Itaque major circulus Solem refert, reliqui Planetas juxta Solem positos ut vera eorum tum inter se tum ad Solem magnitudinis ratio appareat.  Ea vero & ex distantiarum & ex diametrorum telescopio observatorum comparatione constituta est; quemadmodum in his, quae de Saturni mirabilibus formis olim conscripsimus [^], est explicatum.  Sunt quidem haec Planetarum corpuscula ad Solis magnitudinem multo exiliora, quam ab astronomis qui ante nos fuere sunt prodita.  E quibus prisci illi qui nec orbium inter se rationem cognitam habebant, & nudo visu atque indiligenter prorsus Planetarum diametros metiebantur, non mirum est si longissime aberrarunt; recentiores vero, quique invento jam telescopio scripsere, etiam hi non parum ab hisce mensuris nostris diversi abierunt.  Quas equidem veriores esse adseverare non vereor, quod & [437] majoribus organis visoriis haec sidera nos observavimus & certiori ratione diametros dimensi simus. Itaque quae Solem inter caeterosque   *)  Sur la plaque de devant du planétaire Huygens a fait graver — comparez la Pièce VI de la p. 332 qui précède —:   Sciendum est, si ad hanc orbium planetariorum magnitudinem veris proportionibus caetera referantur, Terram tunc planetasque omnes fore ea parvitate quae cerni omnino nequeat. Solem exigui puncti instar; duploque fere, quam sol, minore diametro orbitam Lunae.  Extremorum vero, Jovis et Saturni, comitum orbitas non majores hujusmodi circellis O O.

[ 603 ]

[ v ]

Planetas hic cernitur expressa ratio, ea certa est, atque a vera vel nihil vel minimum quid diversa. 11)  Una tantum Telluris minus liquido comperta est, quam nos hac ratione definivimus; ut sicut loco inter Martis & Veneris stellas media est Tellus, ita ponatur & magnitudine 12); exinde distantia Solis circiter 12000 Terrae diametrorum efficitur, Terraeque diameter ad Solarem ut 1 ad 110 13); quas tamen mensuras subtilissima illa parallaxium observatio a summis astronomis postea adhibita, qua Veneris perigaei distantiam ad calculos revocarunt, egregie confirmavit 14).    11)  ... Avertissement [583*)] ... celui du "Cosmotheoros" [668-670] ... p. 199. [ *)  Corr. 583, l. 6:  Roemer n'avait pas donné dans son planétaire la place centrale à la terre (894). Cf. XXII, 724.]    12)  ... déjà rappelé ... p. 308 ...    13)  ... Huygens avait laissé le nombre en blanc. Dans le "Systema Saturnium" ... 1 : 111. Comparez p. 622, n. 25.    14)  Nous ne croyons pas qu'en parlant de l'observation de "certaines parallaxes" Huygens ait en vue une mesure de la parallaxe de Venus ...

[ 605 ]

[ v ]

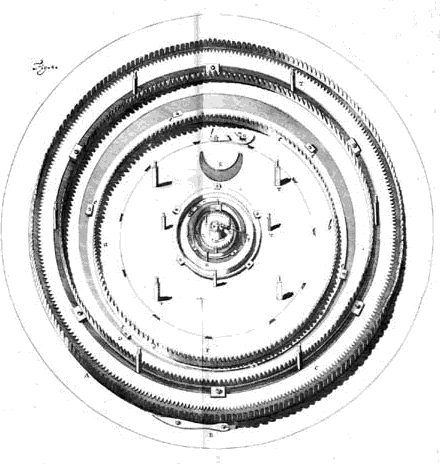
{Vide Tab. 2. Fig. 3.}   Motus autem, qui in hoc Automato cernitur, ratio converso pegmate, inspectaque intus machina cognoscitur.  Reducto enim quod hac parte eam claudit operculo, apparet intus lamina ex aere octogonum totum, uti anterior, occupans, atque ab illa anteriore pollicis unius intervallo remota, & columellis pluribus conserta.  Porro axis quidam ferreus hic apparet bipedalis transversim objectus, ac totidem, quot sunt Planetae, rotis instructus, quarum unaquaeque cochlea una per modiolum trajecta affigitur.  Harum rotarum dentes dentibus majorum rotarum Planetas singulos circumferentium, interque binas laminas jacentium aptantur.  Porro eidem axi communi alia praeterea rota insidet circulo dierum ac mensium convertendo destinata; itemque cochleae, quam

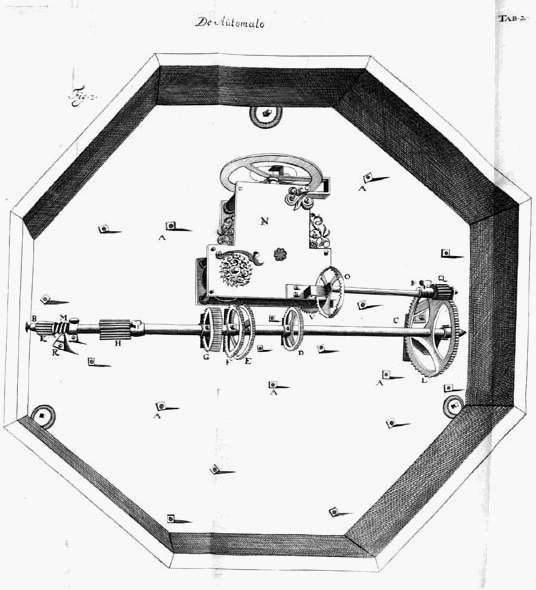
[ 607 ]

[ v ]

infinitam vocant, particula, quae circulum cum inscriptis annis trecentis, totidem annorum spatio semel circumducit, intercedente axiculo quodam dentato.   Positum vero axis ferrei quod attinet, is horizonti quidem parallelus est, non autem laminae magnae quam [438] jam demonstravimus, sed parte ea, quae inspicienti dextra est, multo magis ab illa recedit, quod ita faciendum fuit, ut commodius unius axis conversio omnium planetarum diversis motibus sufficeret.   Dentium vero numeri certa ratione, quam mox exponemus, reperti sunt, tamque exacte mediis motibus aptati, ut in annis viginti Saturnus tantum scrupulo 1, 34" promovendus sit, Jupiter 1', 9". Mars 24', 0". Venus gradibus 3. scrup. 37'. Mercurius 7', 47". Luna parte 1, scrup. 31'. 15)  Caeterum non tantum motus medios exhibuimus, sed & cum inaequalitate ea quae reipsa planetarum cursibus inest; idque secundum anomalias a Keplero excogitatas, quarum apud astronomos maxima auctoritas.  Quo pacto autem haec inaequalitas conficiatur suo loco ostendemus.   Porro etiam horologium Automaton hac parte conspicitur paulo supra axem dictae laminae adfixum, cujus horologii vi axis ille magnus annuas conversiones facit, ac per eum omnia continuo motu cientur; transit enim motus ab horologio in rotam [L] axi infixam quam dierum ac mensium circulo aptari diximus, quemadmodum in adscripto typo apertius liquebit.  Interiora horologii percensere nihil necesse est, cum vulgo notum sit inventum, cujus nimirum vis a lamina in helicem convoluta.  Hic vero motus aequalitatem alia 'helikôdei' lamina adjuvimus*), quae libramento recursus temperaret; quod alterum post inventa pendula remedium excogitavimus non aeque tutum quidem, quod frigore & calore elater vires suas paulatim quid intendat ac remittat, sed hic aptius convenientiusque.  Intenditur autem lamina illa prior motus effectrix septenis quibusque diebus. [439]    15)  Ceci s'accorde avec la table de la p. 176 ... Voyez aussi ... p. 581, n. 3.   [ *)  Cf. fig. 21 (photo) dans T. XVIII, vis-à-vis p. 525 — Museum Boerhaave.]

[ 609 ]

[ v ]

E X P L A N A T I O TAB.  2.   FIG.  3.  A.A. Sunt lamellae quadratae, quae columellarum Fig. 4. Tab. 3. litteris  TT.  designatarum capita cochleis astringunt.   C.B. Est axis bipedalis ferreus.   D. Est rota, quae Mercurii rotas movet constans dentibus 121.   E. Rota Veneris constans dentibus 52.   F. Telluris, dentibus 60.   G. Martis, dentibus 84.   H. Jovis dentibus 14.   K. Saturni dentibus 7.   L. Rota dentium 73. movet circulum, cui menses diesque inscripti sunt.

[ 611 ]

[ v ]

M. Est cochleae infinitae particula, cujus convolutio annorum 300 circuitum efficit, intercedentibus binis rotulis communi axiculo Tab. 3. designato  E  affixis; quibus singulis dentes 6. quarumque altera huic cochleae convenit; altera interior rotae annorum 300. dentibus inseritur.   N. Horologium.   V. Rota est, per quam horologium movet axim  CB.   P. Sunt dentes quatuor in extremitate axis rotae  V.   O. Rota, quae a dentibus  P.  movetur, & dentes habet 45.   Q. Tympanum est axi rotae  O.  inhaerens constans dentibus novem, quibus movetur rota  L  & per eam axis.   R. Est lamella aerea huic laminae majori affixa, cujus orificio parvulo inhaeret annulus dentatus  E  Tab. 3. depictus.  [440]   {Vide Tab. 2. Fig. 3.}   In schemate adscripto, quae conversae machinae faciem amoto operculo exhibet, lamellae quadratae, quibus adscriptum est A, reliquaeque iis similes, eae columellarum capita cochleis adstringunt, quibus columellis laminae, quae hic cernitur, connectitur anterior illa Planetarum orbibus in partes dissecta.   Axis bipedalis ferreus est CB, parte ea, qua C adscriptum est, pollices binos a lamina distans.   In hoc axe defixae rotae orbes planetarum circumagunt, D quidem Mercurii, E Veneris, F Telluris, G Martis, H Jovis, K Saturni.  Circulum vero cui menses diesque inscripti sunt rota L movet, ac denique annorum 300 circuitum efficit cochleae M convolutio, intercedentibus rotulis binis communi axiculo affixis, quibus singulis dentes 6, quarumque altera cochleae huic convenit, altera interior rotae annorum magnae dentibus inseritur.   Per unum igitur axem CB annuas conversiones peragentem, (namque & rota L & cochlea M ipsi inhaerent) tot motuum diversitas perficitur; axis autem ab horologio hoc modo cietur.  Est in horologia rota V, cujus hic particula tantum cernitur horis 96. singulas conversiones faciens.  Hujus axi altero capite ad P dentes additi sunt quaterni, hi inseruntur rotae O dentibus 45. cui rotae in communi axi jungitur tympanum Q. novem dentibus incisum; qui denique aptantur dentibus 73 rotae L.   Oportet nunc & interjectas utrique laminae planetarum rotas inspiciundas dare, ut quomodo constructae sint & quo pacto circumeant, appareat.  [441]

[ 613 ]

[ v ]

Fig. 4.	De Automato.   Tab. 3.	Fig. 6.
Fig. 5.		E

E X P L A N A T I O TAB.  3.   FIG.  4.  A. Rota Saturni constans dentibus 206.  B. Brachiolum, cui Saturnus infigitur.  C. Rota est, cui anni trecenti inscribuntur, ut annum designet illo temporis spatio semel circumvoluta. Constat dentibus 300. Circumvolvitur autem ope cochleae infinitae, quae in Tab. 2. Fig. 3. littera  M  designatur, idque ope axiculi dentati  E.  D. Rota, quae mensem diemque mensis sua circumvolutione ostendit, constans dentibus 219.  [ E. Axiculus dentatus, vide C. ]   F. Rota est, quae circumducit Jovem brachiolo  G  infixum. Constat dentibus 166.  [ G. Vide F. ]   H. Rota Martis cum suo Brachiolo constans dentibus 158.   I. Rota telluris simul cum Luna, quae habet dentes 60.   K. Circulus dentatus, qui fixus inhaeret anteriori laminae totius machinae, & qui, dum rota Telluris circumducitur, movet rotulas, quibus Tellus simul cum luna infigitur. Habet autem dentes 137.   L. Rota Veneris, constans dentibus 32.   M. Rota Mercurii dentes habens 17.   N. Axis fixus, cui ab altera parte Sol infigitur.

[ 615 ]

[ v ]

O. Axiculus Mercurii una ex parte infixus axi Solis, ex altera columellae  P  lamellae Telluris immobili insistenti. Habet autem ille duas rotulas, quarum illa  R , quae movet Rotam Mercurii, habet dentes 7. altera vero  Q  dentes 12. Hic autem axiculus ita supra planum hujus figurae elevatus est, ut Rotae Veneris & Mercurii sub eo motus suos exercere queant.  [442]  [ PQR. Vide O. ]   S. Apertura per quam lamina horas monstrans circumducitur.  T.T.T.T Designant columellas, quibus haec omnia illi laminae quam secunda Tabula Fig. 3. repraesentat affiguntur cochleolarum ope. ab. Est annulus planus, quo Planeta circumvolvitur. cd. Armilla dentibus incisa. ee. Repagula annulum planum in ambitu continentia. lm. Brachiolum.  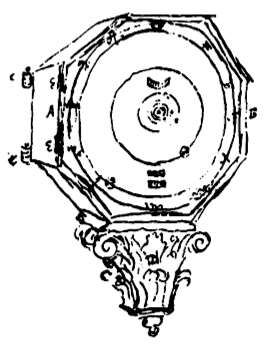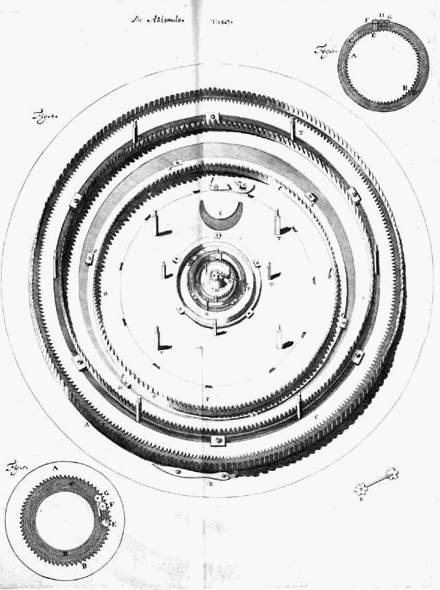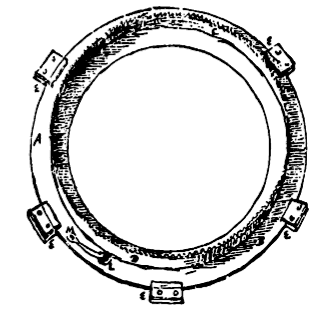[ m axiculus, l tubulus.]   Singulis igitur Planetis annulus planus ad orbitae eorum amplitudinem dicatus est, cui armilla dentata rectis angulis insistit, aequaliter undique ab annuli peripheria distans.  Annulus iste Tabulae octogonae anteriori intus applicitus globulum, Planetae corpus referentem, circumfert, stylo exiguo sibi infixum, quo extra laminam anteriorem tantillo promineat.  In circumferentia annuli hujus repagula quedam collocata sunt laminaeque adfixa intra quae circulari motu ipsi moventur, simulque ut ne a jam dicta lamina recedant continentur.  Horum in Planetis superioribus Saturno ac Jove quina aut sena adjecta sunt propter annulorum magnitudinem, in reliquis quaterna aut trina sufficiunt.   In figura {Vide Tab. 3. Fig. 4.} hic descripta annulus planus est ab, super hunc erecta armilla ac dentibus

[ 617 ]

[ v ]

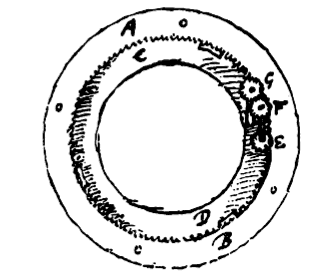
Jam de menstruo Lunae motu ostendendum qua ratione ordinatus sit. {Vide Tab. 3. Fig. 5.}   Inter Martis ac Terrae orbitas quod interjacet laminae Planetariae segmentum, in eo intus defixus est annulus, interiore circumferentia dentes habens 137, quem in hoc schemate significant inscriptae literae A B.  Circumferentia haec dentata paulo major est orbita terrae annuâ, atque ipse annulus AB paulum supra planum, cui affixus est, attollitur, ut sub ipso collocari queant repagula, intra quae volvitur annulus Tellurem ferens, qui notatus est literis C D.  Hic porro annulus axiculum circumfert ad rectos angulos sibi insistentem, rotulasque utroque capite affixas habentem E, F, quarum inferior duodenos dentes

[ 619 ]

[ v ]

habet commissos dentibus [444] annuli AB, superior tredecim.  Superioris dentes inseruntur dentibus 12 rotulae G juxta collocatae, axemque itidem annulo CD infixum habenti, qui quidem axis cavitatem habet in partem anteriorem tabulae Planetariae patentem, in quam cavitatem defigitur stylus exiguus ac lunari circello conjunctus.  Caeterum nec retinaculum quoddam annulo CD affixum & utrosque, quos diximus, axiculos parte superiori detinens, uti nec armillam dentatam exprimendam duxi, ne quid rotularum E F conspectum impediret.   Revoluto itaque annulo Terrestri CD secundum ordinem literarum AEB, quae revolutio anteriori tabulae parte spectata incedit secundum ordinem signorum zodiaci; necesse est contrario motu circumire rotulas E & F, atque huic rursus contrario rotulam G, hoc est, in partem eandem cum annulo Telluris: diximus autem in axem cavum rotulae G stylum inseri, cui cohaeret orbiculus Lunam in circumferentia gerens, Tellurem

[ 621 ]

[ v ]

vero in centro; quare recte ordinatus est Lunae circuitus; quam bene vero tempori Mensis Periodici conveniat inferius manifestum fiet.   Expositis hactenus singulis machinae partibus, dicemus jam, quibus semidiametrorum inter se proportionibus, quibusque centris orbitas Planetarum in tabula anteriore descripserimus, item ubi Apheliorum ac Nodorum puncta constituerimus; deinde quem dentium numerum rotae cuique tribuerimus, ut mediorum motuum constaret ratio, deque ejusmodi numerorum inventione; ac denique qua dentium constructione debitas motuum anomalias expediverimus.   Igitur octogonae laminae statuta hac magnitudine, ut quae ex centro in latus perpendicularis ducitur sit pollicum 11½, centro eodem, ubi & Sol collocandus, circulum [445] Eclipticae signorum descripsimus radio pollicum 10 2/3 . {Vide Tab. 1. Fig. 1.}  Hunc circulum in partes 360 partiti sumus, Signaque 12 suis locis adscripsimus, collocato Arietis signo in parte, quae spectanti ad dextram est, ac pari cum centro altitudine.

Porro Apheliorum loca in laterculo adjecto notata, in quam partem uniuscujusque Planetariae orbitae centrum sumptum fuerit, declarat.  Ex proportione vero semidiametrorum juxta collocata etiam mensura harum linearum intelligitur, si una ipsarum quae est orbitae Telluris semidiameter definita fuerit, quam quidem pollicis unius statuimus, seu pedis Rhenolandici duodecimam partem, qualium enim haec partes 100000 continere censetur, talium radii orbitarum caeterarum partes in laterculo descriptas habent.  Earundem quoque partium sunt excentricitates hic adnotatae, quas ex centro Eclipticae, ubi locus Solis, versus Apheliorum loca accipere oportet, atque ibi centra cujusque orbitae signare.   Ita ex. gr. Saturni orbitam descripturus initio Anni Christi 1682. lineam ex Eclipticae centro duco ad Sagittarii grad. 27, scr. 40'. in ea pono ex centro eodem particulas 54, qualium semidiameter orbitae telluris sive pollex unus 100 continet, non possumus enim in hac parvitate ulteriores minutias prosequi.  Ita centrum orbitae Saturni reperio.  Tum deinde accepto semidiametro partium earundem 951, orbitam Planetae describo, cujus Aphelium signo litera A ad intersectionem rectae ejus, quam ex centro ductam ostendi.  Cum vero orbitae Planetariae in coelo omnes non nihil declinent a plano Eclipticae seu plano orbitae telluris, quod planum hic ipsius tabulae superficies esse intelligitur; ut nimirum dimidiâ sui parte supra attollantur, altera dimidia infra descendant, perspicuum est, non esse ipsas Planetarum [446] orbitas, quae a nobis sunt descriptae, sed lineas ejusmodi in quas incidunt ductae in Eclipticae planum perpendiculares ex orbitarum quibuslibet punctis, quas tamen lineas pro orbitis ipsis habemus, quod secundum illas Planetae motus in longitudinem examinetur; revera autem sunt orbitae ad Eclipticae planum reductae.  Itaque puncta bina, quibus orbita quaeque

[ 623 ]

[ v ]

planum Eclipticae intersecat (hi nodi vocantur) suis signis & notavimus, quorum illud nodo ascendenti tribuitur, unde nimirum Planeta ad partes Eclipticae boreas feratur, quas supra tabulam existere intelligendum; alterum nodo descendenti, quo praeterito in partes austrinas transeat.  Hi vero in eadem linea recta per Solis centrum ducta oppositos locos obtinent communi Astronomorum consensu, etsi non plane ad amussim res sese hoc modo habere videatur [J.d.S], ut suo loco amplius declarabitur.  Caeterum loca nodorum ascendentium; Et quali angulo plana orbitarum Planetarum ad Eclipticae planum inclinentur in tabella hic expressimus; auctores eos secuti qui maxime nobis probandi videntur; adeoque in Venere & Mercurio recentissimorum adhibitis observationibus, quibus in Sole ipso hi Planetae apparuerunt. [447]

ANNO 1682.  Januarii 1mo.  22)

Aphelia.

Nodi ascendentes.

Inclinationes.

Semid. or-  bium Pla- netarum.

Excentricita-  tes in iisdem partibus.

Gr.

/

//

Gr.

/

//

Gr.

/

//

Mercurii

15 :

11 :

19

14 :

29 :

47

6 :

54 :

0

38806

8149

Veneris

2 :

59 :

44

13 :

54 :

52

3 :

22 :

0

72400

500

Martis

0 :

30 :

17

17 :

38 :

12

1 :

50 :

30

152350

14115

Telluris

7 :

7 :

20

100000

1800

Jovis

7 :

55 :

43

5 :

30 :

42

1 :

19 :

20

519650

25058

Saturni.

27 :

39 :

46

21 :

36 :

26

2 :

32 :

0

951000

54207

Diam. annuli Saturni	ad diamet. Solis	ut	11	ad	37	25)
Diam. annuli	ad diametr. globi Saturn.	ut	9	ad	4
Diam. Iovis	ad diametr. Solis	ut	2	ad	11
Diam. Martis	ad diametr. Solis	ut	1	ad	166
Diam. Terrae	ad diametr. Solis	ut	1	ad	110
Diam. Veneris	ad diametr. Solis	ut	1	ad	84
Diam. Mercurii	ad diametr. Solis	ut	1	ad	308

22)  ... valeurs empruntées aux Tables Rudolphines ... p. 148-9 qui précède ... excepté dans le cas du noeud ascendant de Mercure ... p. 177  [Gallet, JdSç, 20 dec. 1677].    25)  Avec l'exception de ce qui se rapporte à Mercure, on trouve tous ces rapports dans le "Systema Saturnium" de 1659 ... 1 : 111 au lieu de 1 : 110.  [p. 81]

[ 625 ]

[ v ]

Porro ut apparentes Planetarum latitudines cognoscere liceat super linea recta nodos oppositos jungente arcus circunferentiae circularis utrinque descripsimus, alterum extra orbitae portionem boream, alterum intra portionem australem, tanto intervallo ab ipsis portionibus, ubi maxime absunt, recedentes, quanto orbita ipsa supra atque infra planum Eclipticae iis ipsis in locis extare deberet; atque ibidem angulos inclinationis adscripsimus.  In quocunque vero orbitae suae reductae puncto Planeta reperietur, si ab eo puncto ad adscriptum arcum minima distantia accipiatur, ea quam proxime intervallum indicabit, quo ab Eclipticae plano illic vera Planetae orbita recedit, quod intervallum cum distantiâ Planetae a Tellure comparando, ipse quoque [448] latitudinis angulus ex triangulorum doctrina facile investigabitur; atque haec de exteriore Automati forma deque usu ejus dixisse sufficiat:  Nunc ad interiorem fabricam pergamus.

[ 627 ]

[ v ]

Dentium in rotis numerus hoc modo a nobis inventus fuit; Motum Medium cujusque sub Ecliptica Planetae annuum seu dierum 365 ad Telluris Medium annuum motum, quales in Tabulis Astronomicis exhibentur, comparavimus; reductis ad tertios scrupulos arcubus eorum motuum integris.  Numeri hinc orti, cum eam inter se proportionem habeant, quam arcus circulorum eodem tempore a Planeta, atque a Tellure in orbitis suis emensi, sequitur tempora utriusque Periodica ejusdem rationis contrariam continere; quam itaque, vel similem minoribus numeris expressam, etiam dentium numeri habere debent, quibus nempe rota tum Planetaria, tum altera ipsi congruens, atque axi magno imposita incidantur; singulis enim axis hujus conversionibus Tellus integram orbitam suam percurrit; quoniam aequalem dentium numerum rotae Tellurem ferenti, itemque ei, quae in axe magno respondet, attribuimus, sexagenarium puta, vel alium pro lubitu, qui commode in rotas inducatur.   Huc itaque res tota recidit ut datis numeris duobus magnis certam inter se rationem habentibus, alii minores inveniantur rotarum dentibus multitudine sua non incommodi, quique eandem proxime rationem ita exhibeant, ut nulli ipsis minores propius.  Sed exemplo rem totam melius exponemus; Sunto igitur inveniendi dentes in rota Saturni, inque minore illam movente, quae axi magno est imposita, quam indicabat superius litera K. {Vide Tab. 2. Fig. 3.}  [<]   Annuus Saturni motus (sequor autem tum in hoc tum in caeteris Riccioli recentissimas Tabulas) proditus [449] est gr. 12, 13', 34". 18'".  Annuus Telluris, quem ille Solis vocat, gr. 359°, 45', 40", 31'". 31)  Reductis igitur omnibus ad scrupula tertia, fit proportio   31)  "Astronomia reformata" Lib.I, cap. IV ... p. 179 qui précède [ref. Almagestum novum].

[ 629 ]

[ v ]

2640858 ad 77708431.  Itaque quam rationem habet posterior horum numerus ad priorem, eam habet Saturni tempus Periodicum ad tempus, quo circa Solem Tellus convertitur, ac proinde & rotae Saturniae dentium numerus ad suae motricis rotae dentes hanc rationem quam proxime servare debet.  Inveniendis igitur numeris minoribus qui proxime rationem istam exprimunt; divido majorem per minorem, & rursus minorem per eum qui a divisione relinquitur, & hunc rursus per ultmimum residuum, atque ita porro continenter pergendo*) invenio quod fit ex primâ divisione 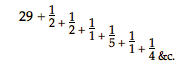nempe numerum cum adjuncta fractione, cujus fractionis numerator est unitas, denominator vero rursus fractionem adjunctam habet, cujus numerator unitas, denominator similiter ac praecedens componitur; idque ita consequenter; qua via, si, quo usque potest, continuetur, eo devenitur, ut a divisione tandem unitas supersit.   Jam ab hac fractionum serie posteriores aliquousque praecidendo, velut hic 1/5 cum caeteris deinceps sequentibus, reliquasque cum numero ipsas praecedente reducendo ad communem denominatorem, erit hujus ad numeratorem ratio propinqua ei, quam datorum numerorum minor habet ad majorem; adeo quidem ut minoribus numeris propius ad eam accedere non liceat. [450]  Reductionis modus facilis est; nempe posteriores, unde hic incipimus fractiones, , tantundem valent ac 1/3, unde ad   [ *)  Fraction continue,  C. Brezinski, 'Ces étranges fractions qui n'en finissent pas' (^);  Continued fractions'.]

[ 631 ]

[ v ]

proxime praecedentem pergendo ac reducendo , faciunt 3/7; denique & numerum integrum includendo ac reducendo 29 + 3/7 fiunt 206/7.  Itaque numeri 7 ad 206 propinqua ratio est rationis 2640858 ad 77708431.  Eoque rotae Saturniae dentes 206 dedimus, ipsam vero moventi dentes 7.  Quod autem minores numeri non inveniuntur, qui propius rationem propositam exprimunt, ita ostendemus.  Principio certum est numeros hujusmodi reductione factos, esse inter se primos, ex. Prop. 1. l. 7. Elem. [^] quia nihil aliud est divisio nostra continua quam subtractio illa Euclidea, quae si numeris nostris 206 & 7, reductione effectis adhibeatur, planum est unitatem tandem relinqui, quia fractionum istarum omnium numerator est unitas.  Quod si jam duo quivis alii numeri propius ad proportionem magnorum accedunt, eos necesse est, facta continua divisione majoris per minorem, donec unitas supersit, quotientem efficere 29, cum fractionibus iisdem, quae supra, continue adjectis, atque ulterius continuatis quam unde reductionem incepimus, cum inveniremus numeros 7 & 206.  alioqui enim ad primae divisionis quotientem qui dictas fractiones omnes quousque possunt continuatas adjectas habet propius accedi nequit.  Sic quoniam continua divisione 206 per 7, invenitur necesse esset divisione simili numerorum propiorum unam saltem insuper fractionem istis adjici, vel 1/5 vel aliam qua propius ad quotientem universalem perveniatur, [451] quam si ad 1/1 subsistamus.  Hinc vero facta reductione, manifestum est, numeros majores effici, quam si a citeriori fractione caeptum fuisset, quandoquidem accessione cujusque fractionis reductae efficitur fractio constans numeris inter se primis, quaeque propterea ad minores reduci nequit; quod examinanti manifestum fiet si ad sequens theorema attenderit demonstratu facillimum:  nempe Propositis duobis numeris inter se primis, eorum alteruter ad se ipsum vel sui multiplicem altero numerorum auctum primus erit.  Si enim non, ergo ita compositum metietur, sed & partem metitur, hoc est, se ipsum, vel

[ 633 ]

[ v ]

sui multiplicem; ergo & reliquum metietur; quod absurdum, quandoquidem numeri inter se primi ponebantur.  Itaque propiores numeri proportioni propositae, non minores, sed majores erunt inventis 206 & 7.   Porro facile intelligitur reductionem fractionum ab ea utilius semper incipi, quam proxime insequens fractio majorem denominatorem habebit vicinarum comparatione; sicut & antecedenti exemplo inde reductionem incepimus, ubi 1/5 sequebatur.   Utilitas vero methodi ad alia multa porrigitur, ubi proportio quaepiam numeris comprehensa ad proxime aequalem aliis minoribus numeris est redigenda.  Velut cum peripheriae circuli ad diametrum ratio ad notas veras plures datur, nempe quae 31415926535 ad 10000000000.  Hîc facta divisione fit, 35) 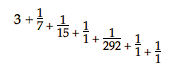ubi si reductionem inchoaremus a fractione 1/7 fit proportio Archimedea 22 ad 7, si vero ab 1/1 fit alia multo propinquior quam Adr. Metius prodidit 355 ad 113; sicut enim [452] 113 ad 355 ita 10000000 ad 31415929 &c.  Eodem modo hic alias ad verum propius accedentes rationes invenire licet; sed haec Metiana, cum ad usum habilis est, tum pro numerorum parvitate eximia, ob exiguam particulam 1/292 citra quam reductio coepta est; Cujusmodi non facile similis reperitur ulteriores numeros tentanti.  Sciendum vero, reductione hac nostra majorem proportionis terminum alternis majorem minoremve vero reperiri, prout a prima, tertia, quinta aut alia deinceps impari fractione reductio inchoata fuerit.  Ita cum a tertia fractione, quae est 1/1 reductionem praecedentem inceperimus, fit proportio circumferentiae ad diametrum, ut 355 ad 113 major vera; at si a secunda quae est 1/15 incepissem, extitisset inde proportio 333 ad 106 minor verâ; rursus si a prima quae est 1/7 initium fiat oritur proportio Archimedea 22 ad 7 major vera;   35)  ... p. 394 du T. XX.

[ 635 ]

[ v ]

veram autem proportionem hic appello, quae iis, qui adsumti sunt, magnis numeris exprimitur, quam nimirum pro ipsa proportione circumferentiae ad diametrum accepimus.  Horum vero demonstratio hoc fundamento nititur notissimo, Fractionem quamcunque, aucto denominatore, fieri minorem; imminuto, majorem.   Sit enim numerus ex prima divisione ortus A, fractionibus vero deinceps descendentibus quotlibet B C D E F & ad infimae F denominatorem adjecta intelligatur fractio quae ex omnibus ulterioribus fractionibus reductis conficeretur, quae dicatur Z.  Cum itaque fractio, cui superscriptum F, sit major vera, quia denominatorem habet minorem vero denominatore, qui esset 1 + Z, hinc augendo denominatorem fractionis E fractione F, fiet reducta fractio ex fractionibus E, F, minor vera, ideoque rursus augendo denominatorem fractionis D, ista fractione [453] reducta, fiet fractio ex D E F reductis major vera, ac proinde rursus augendo denominatorem fractionis C ista ultima, fiet fractio, ex C D E F fractionibus reductis, minor vera. 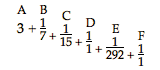  Cumque ita necessario fractiones ex reductione fractionum sursum tendendo effectae, alternatim nunc majores, nunc minores evadant Veris, sitque infima, unde initium fit, semper vera major; facile apparet, si haec sedem imparem obtineat, etiam ex omnium fractionum reductione effectam vera majorem fore, ideoque numero A additam, daturam terminum proportionis majorem vero.  Si vero illa, unde initium fit, sedem parem obtineat, tum ex reductione omnium exstituram fractionem vera minorem, ac proinde numero A additam, daturam terminum proportionis vero minorem.  Quare patet propositi veritas.  Sciendum porro, si omnes ordine terminos proximos datae proportioni desideremus, tunc & ab omnibus fractionibus imparium sedium, & rursus ab omnibus sedium parium faciendam reductionem, idque ita, ut pro singularum fractionum denominatore, qui unitate major erit, ponantur seorsum denominatores omnes ab unitate ad illum usque, & cum iis singulis reductio inchoetur perficiaturque.  Hoc enim si fiat in fractionibus sede impari locatis, omnes termini veris majores ordine existent; si verò fiat in fractionibus sedium parium, habebuntur ordine omnes termini veris minores.  Ita in proposito exemplo si pro fractione prima 1/7 ponantur sigillatim [singulatim] 1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, facta hinc reductione existent proportiones vera majores: 4 ad 1, 7 ad 2, 10 ad 3, 13 ad 4, 16 ad 5, 19 ad 6, 22 ad 7.  deinde a fractione tertia D incipiendo fiet [454] proxima ratio major 355 ad 113.  Et ab quimta F incipiendo fiet proxima ratio major 104348 ad

[ 637 ]

[ v ]

33215.  Rursus si pro fractione secunda 1/15 ponantur singulatim 15 fractiones, 1/1, 1/2, 1/3, &c.  Item pro quarta 1/292 ponantur omnes ab unitate, 1/1, 1/2, 1/3, usque ad 1/292; factis reductionibus habebuntur ordine proportiones veris minores, quae quidem ad fractionem E procedendo dari possint.  Quod si denique seriem continuam mixtam terminorum tam majorem quam minorem vera proportionem exhibentium velimus, quorum quique praecedentibus ad veram propius accedant, tunc hoc observandum, ut in fractionibus quibusvis, quarum denominator unitate major erit, ponantur, non ut modo factum omnes deinceps minores denominatores ab unitate, sed ab ea incipiendo quae dimidio illius denominatoris proxime major erit.

[ 639 ]

[ v ]

Hac igitur ratione in caeteris quoque Planetis usi, rotae Jovis dedimus dentes 166, rotae vero ipsam moventi dentes 14.  rotae Martis dentes 158, ipsam vero moventi dentes 84.  Rotae Veneris dentes 32, ei quae movet dentes 52; qui numeri sunt inter se ferme, ut 70 ad 43.  Quibus numeris si usi essemus, & Rotae Veneris dedissemus dentes 43, rotae vero hanc in axe magno agitanti, 70, aliquantulum perfectius vero Veneris motui respondisset Machina.  Priores enim numeri, quos adhibuimus, efficiunt, ut Venus post 20 annos a vero loco deficiat gr. 3, 37'. cum posteriores in iisdem 20 annis tantillulum ultra verum locum Venerem promoveant, sed excessu 15'. non plene aequante.   Nec multum dissimili ratione inveniuntur dentes rotularum, quae Mercurium movent.  Assumta enim Periodo telluris sub Ecliptica dierum 365. hor. 5. 49'. 15". 46"'., Mercurii vero sub eadem dierum 87. Hor. 23. [455] 14'. 24", aut facilitatis ergo assumta illa d. 365. hor. 5. 50' & hac dierum 87. Hor. 23. 15'. invenietur ratio revolutionum Mercurii ad illas Telluris ut 105190 ad 25335, sive 21038 ad 5067; quorum divisione, eo, quod dictum, modo, instituta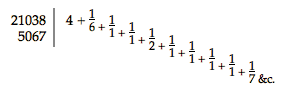

[ 641 ]

[ v ]

& neglecta ultima fractione reliquis ad communem denominatorem deductis fiet 847/204, qui numeri proportioni motuum, quibus hi Planetae moventur, quam proxime respondent.  Verum cum 847 fiat ex ductis in se numeris 121, & 7, & 204 ex ductis in se numeris 12 & 17, rotae annuae, quae est in axe communi, inditi sunt dentes 121 [fig. 3: D], & axiculus interpositus rotatilis circa duo puncta fixa {Vide Tab. 3. F. 4.}, quorum alterum est in axe per Solem & annulum Mercurii transeunte; alterum in columella inhaerente lamellae fixae Telluris.  Sunt autem haec puncta ita remota ab ipsis orbitis Mercurii & Veneris, ut dentes rotarum Veneris & Telluris libere sub axiculo transeuntes ab eo in motu suo non impediantur;  Hic autem axiculus duas rotulas habet circa unamquamque extremitatem unam, quarum altera, cujus dentes committuntur rotae annuae, est dentium 12; altera vero, quae armillae dentatae Planetam vehenti committitur dentium 7, cum ipsa armilla habeat dentes 17.  quo ipso inter motum axis communis, & rotae Mercurium vehentis eandem proportionem servari, quae est 204 ad 847, manifestum est. [456]   Rotularum, quae Lunam vehunt dentes ut inveniantur, assumto eodem motu annuo d. 365. hor. 5. 50', & Lunari motu d. 29 hor. 12, 44', 3" sive scrupulorum 45, ob faciliorem calculum invenietur ratio revolutionum Lunae ad eas Telluris, ut 105190 ad 8505, sive 21038 ad 1701: quibus numeris, ut prius, divisis fit 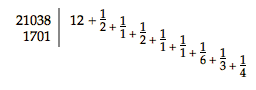Quod si pro ultima fractione sumatur 1/6, & praecedentes ad eundem denominatorem deducantur, fient numeri 1546 & 125, quorum cum prior nullas partes aliquotas habeat, praeter 2 & 773; hic, autem nimium dentium numerum faciat, praestabit si loco fractionis 1/6 proxime minorem sumamus 1/7, quo facto orientur numeri 1781 & 144, quorum prior fit ex 137 & 13, posterior ex 12 in 12.  Ex quibus descripta [<] ratio dentium tum in majori rota, tum in minoribus axiculis dentatis facile constabit.   Ex ipsa autem hac inventione numeri dentium, qui tum in axe communi, tum in rotis singulos Planetas deferentibus incidi debent, manifestum est non posse has

[ 643 ]

[ v ]

circumvolutiones ita fieri, quin tractu temporis aliquantulum ab ea ratione quam motus telluris ad motum uniuscujusque Planetae ex observatis habere assumsimus, aberret; Cujus tamen aberrationis quantitatem, quantula sit, facile est determinare.  Nam ut exacte in machina eadem ratio veri motus observaretur, necessum foret, [457] ut ratio motus praecise numero dentium in rotulis respondeat.  Nimirum in Saturni, ut hoc exemplo res plana fiat, rota, quae in axe communi est, dentes sunt 7, in ea vero, quae Saturnum vehit, dentes 206.  Necessum igitur est, ut tempore 206 annorum Saturnus periodum suam absolvat septies;  Verum cùm ratio motus Telluris ad Saturnum sit, ut 7708431, ad 2640858. invenietur, Saturnum spatio 206 annorum, absolvere periodum suam non praecise septies, sed circiter 7 1/1346.  Singulis ergo 206 annis Saturnus in motu suo in hac machina retardatur 1/1346 sui circuli, singulisque annis tantundem uniuscujusque dentis, & annis 1346 retardabitur ejus motus unico dente, quo igitur post id tempus rota Saturni promovenda erit.  Haec autem rota cum constet dentibus 206, qui integrum circulum 360 graduum constituunt, unicuique denti praeterpropter respondebunt 105 scrupuli, per quos itaque promovendus erit Saturnus post exactos annos 1346, adeoque post 20 annos 1' 34".  Eademque ratio est in caeteris.   Restat explicemus quanam ratione ex harum rotarum revolutione debitae motuum anomaliae sequantur 44).

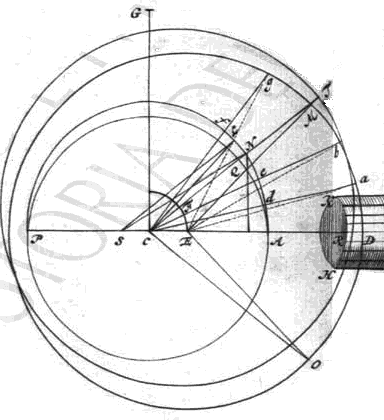
Hunc in finem sit ANP  {Vide Tab. 4 Fig. 7}  orbita Planetae, cujus centrum C; Sol S; sumaturque in SC punctum E ad lubitum, fiatque, ut excentricitas SC ad radium CA, ita CE ad ED, quo radio ac centro E describatur circulus DM.  Intelligatur porro circulo AL super centro suo C mobili affixum esse immobiliter circulum DM incisum dentibus aequalibus super circuli plano erectis, qui proinde circulus necessario quoque circa centrum C movebitur.  Ponatur autem moveri versatione aequabili tympani KH axem ad C directem habentis, cujusque dentes congruant dentibus rotae DM.  Satis enim convenient, etsi ob excentricitatem hujus rotae non semper tympano ad [458] rectos angulos subjiciantur: dico hoc motu Planetam inaequaliter ferri in sua orbita, idque ita, ut ejus motus hypothesi Keplerianae proxime aequipolleat.   44)  Comparez sur ce sujet e.a. les p. 143-148 qui précèdent.

[ 645 ]

[ v ]

{Vide Tab. 4. Fig. 7.}   Sumto enim in circulo DM. centro E descripto quo libet arcu DO, ponatur ejus arcus dentes versatione tympani HK pertransiisse rectam CD, erit necessario recta CO in recta CAD, etsi non ita, ut punctum O sit in D, sed interius in R, cum CD, quae aequalis est duabus CE, EO, major sit, quam CO.  Quantus igitur est angulus OCD, tantus quoque erit angulus, quo recta CAD mota erit circa Centrum C; ideoque si faciamus angulum DCT aequalem angulo DCO, erit CT recta, in quam promota erit CAD, adeo ut Planeta processerit ex A in punctum N, ubi recta CT secat circumferentiam AN centro C descriptam.  Circulus autem DM centro E promoto in F, factoque FT aequali ED, habebit situm circuli TR.  Apparet autem ob eandem angulorum OCD, DCT aequalitatem arcum DM, quem recta CT abscindit in circumferentia ODM esse aequalem arcui DO.  Unde juncta ME, erit & angulus MED aequalis DEO.  Itaque si fiat arcus AL totidem graduum, quot continet arcus DM, jungaturque CL, erit haec parallela EM.  In triangulis igitur CEM, SCL erunt anguli LCS, MEC aequales, & circa hos aequales angulos latera proportionalia.  Est enim ex constructione SC ad CL, ita CE ad EM, quoniam CL ipsi CA & EM ipsi ED est aequalis.  Erunt ergo aequales etiam anguli MCE & LSC, ac proinde latera CM, SL parallela.

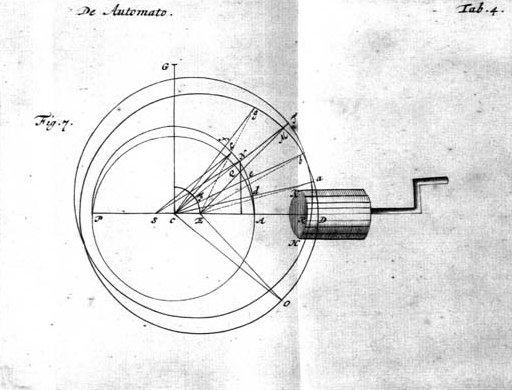
Hac igitur rotatione circulorum DM, AL Planetam in A positum ita moveri per circulum AL, ut ejus motus quam proxime respondeat Hypothesi Kepleri ita ostendetur:  Ponatur Planeta motus ab A versus N, erit spatium NSA anomalia ejus media; atqui propter lineas parallelas SL, CN erit triangulum NSC aequale triangulo CLN, quod insensibili [459] discrimine differt a sectore CLN.  Spatium itaque CLA, adeoque & arcus AL respondebit anomaliae mediae; promoto Planeta ex A in N.  Quod si ponamus AQP esse ellipticam Kepleri orbitam, erit quidem Planeta in Q, ubi scilicet NQ perpendicularis in AP Ellipsin AQP secat, non in N, sed hae Ellipses tam parum a circulis recedunt, ut differentia in machina animadverti nequeat.  Erit itaque N locus Planetae debitus medio motui AL, qui arcus tot gradus, ac arcus DO sive DM complectitur.  Quod si tympanum ponatur quovis alio loco velut in G aeque distante a centro C versus quod tympanum dirigitur, collocetur vero punctum D, quod in rota ODM maxime a Centro C distat sub tympano, & Planeta rursus in A loco Aphelii sui, apparet aequali versatione tympani

[ 647 ]

[ v ]

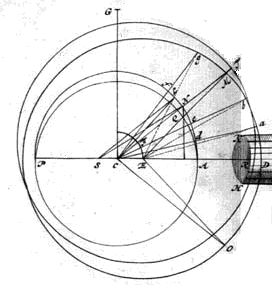in G atque in D eosdem angulos transire circa centrum C.  Quare ubicunque collocetur tympanum, eodem ritu motus Planetae inaequalis fiet, licet dentes rotae DM aequales ponantur, modo dentes tympani K directe spectantis ad punctum C aliquam habeant longitudinem, qua committi queant dentibus circuli DM aliis & aliis in punctis secantis rectam DC; & simul observetur, ut posita recta longissima, quae a centro C ad circulum DM duci potest directe sub tympano K, Planeta ponatur in Aphelio circuli ANL.  Verum cum nostra in machina omnia tympana in uno eodemque axe sint posita, non poterit ille nisi ad duorum Planetarum centra debite collocari; quare porro considerandum est, qui idem per inaequales dentes perfici queat.  Quem in finem supponamus circulum DMP in partes aequales Da, ab, bM, Mg sectum esse, & ad illas singulas duci ex puncto C restas, Ca, Cb, CM, Cg illae in partes inaequales Ad, de, eN, Nf secabunt orbitam Planetae ANL.  Qua ratione invenientur in circulo ANL totidem dentes inaequales, [460] quot aequales positi sunt in circulo DM.  Quibus si nunc porro tympanum K applicetur, (satis enim convenient, licet alibi minores, alibi vero majores paulo evadant,) cum eodem numero dentium tympani K, quo transiere prius dentes arcus DM, jam transeant dentes arcus AN, fiet, ut simul eadem motus Planetae oriatur inaequalitas, quam Hypothesi Keplerianae proxime respondere ostendimus. F   I   N   I   S.   [ Franse vertaling van Antide Janvier in Des révolutions des corps célestes par le mécanisme des rouages, 1812. Ook in:  Pierre Dubois, Histoire de l'horlogerie (1849), p. 162-177. Diens fig. 1-6 ook in L.Reverchon & P. Ditisheim, 'La machine planétaire et l'oeuvre astronomique de Huygens', L'Astronomie: revue mensuelle (Soc. Astr. Fr. 1930), p. 63.]