[ 383 ]

[ Lat. p. 589 ]

BESCHRIJVING  VAN  HET  PLANETARIUM DOOR  CHRISTIAAN  HUYGENS Vertaald uit de "Opuscula Postuma", uitgave van 1703. Lugduni Batavorum, apud Cornelium Boutesteyn DOOR  DR. J. A. VOLLGRAFF  EN  DR. D. A. H. VAN ECK N  AAR het mij voorkomt, bezitten wij de wetenschap van de hemellichamen en hunne bewegingen, welke voor twee duizend jaar ontstaan is en door groote geesten verder ontwikkeld, eerst thans in een afgeronden en volmaakten vorm; met dien verstande, dat men in de laatst verloopen honderd jaren daarin meer vorderingen heeft gemaakt dan in al den vorigen tijd.   Immers, wat betreft hetgeen vroeger in deze kunst het voornaamste was: de plaatsen der sterren, zoowel die der vaste sterren als die der dwaalsterren, te bepalen, den duur van het jaar en van de maanden uiteen te houden, en verduisteringen te voorspellen, niet alleen hebben wij nu geleerd dit alles veel beter en gemakkelijker te doen, maar bovendien kennen wij (hetgeen gewichtiger en luisterrijker is) met volmaakte zekerheid de orde, den stand, de verhouding en de gedaante der hemelbanen, volgens welke de planeten en de aarde zelve zich rondom de zon bewegen; ook hebben wij een ontelbaar aantal vaste sterren en nieuwe evenzoo door waarnemingen met den verrekijker ontdekte planeten aan het getal der reeds bekende toegevoegd.   Al hetwelk vóór den tijd van Copernicus, een deel ervan zelfs vóór onzen eigen tijd, in diepe duisternis verborgen lag.   Wanneer men dus in gedachten houdt, dat de oude sterrekundigen verstoken waren van de kennis van zóó belangrijke tot hun gebied behoorende zaken, zoodat zij noch de afzonderlijke deelen van het Stelsel noch ook den vorm van het geheele Stelsel begrepen hadden, dan zal men ook gemakkelijk inzien, dat het hun onmogelijk was eenig model of beeld daarvan te construeeren.   Hoewel in de geschriften der geleerden zeer vaak de sfeer van Archimedes*) en evenzoo die van Posidonius worden geroemd (welke laatste door Cicero wordt vermeld) zoo is het om de genoemde reden toch onmogelijk dat daarin eenige gelijkenis geweest is met het hemelsche origineel of eenige nabootsing der werkelijke bewegingen, hoewel het aannemelijk is, dat deze sferen   [ *)  Vergelijk Aanhangsel II. Bronnen ook bij Isack Beeckman, 1629v.]

[ 384 ]

[ Lat. ]

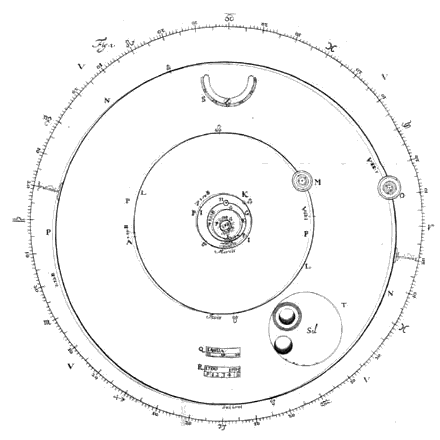
met zeer groote scherpzinnigheid en kunstvaardigheid geconstrueerd waren.   Maar aangezien sedert den tijd, waarin de sterrekunde hervormd en verbeterd is geworden, hetzelfde gemakkelijker beproefd kon worden, zoo is het ook, zooals wij weten, door verscheidene personen ondernomen en uitgevoerd; wij hebben ook eenige der door hen volgens verschillende methoden samengestelde mechanismen gezien. [<]   Wijzelf echter, een van hen allen verschillenden weg gevolgd zijnde, hebben een zoodanig Planetarium laten maken, dat wij daarmede door een klein aantal in elkaar grijpende raderen bereikt hebben, dat op het oppervlak van een platte tafel de lichamen der vijf primaire Planeten rondom de Zon, en evenzoo dat der Maan rondom de Aarde, hunne banen konden beschrijven, in dezelfde tijden waarin zij dat in den hemel 1) doen, en wel in zoodanige excentrische banen, dat deze de ware afmeting en den waren stand der hemelbanen weergeven, met behoud van de bij elk daarvan bestaande ongelijkheid der bewegingen, waardoor zij zich sneller bewegen in minder ver van de zon verwijderde gedeelten, waarbij wij ook nog rekening gehouden hebben met de kleine afwijking tusschen het vlak hunner banen en dat van de Ecliptica of van de Aarde.   Zoodat, afgezien van de bevalligheid van het schouwspel, men daaruit ook de standen van de Planeten kan leeren kennen, niet slechts de oogenblikkelijke, maar ook de toekomende en de verledene, als uit een eeuwigdurenden kalender; en bovendien hun aller conjuncties en opposities, zoowel ten opzichte van de zon als ten opzichte van elkander, en dit des te nauwkeuriger naarmate het werk op grooter schaal is uitgevoerd.   Daar velen naar deze uitvinding gevraagd hebben, die verlangend waren haar of te leeren kennen of haar na te bootsen, zullen wij haren aard in dit boek verklaren. Ik zal beginnen met het buitenwerk van het mechanisme, hetwelk het geheel in zich sluit.   Het is dan een achthoek uit hout samengesteld, met een diameter van twee voet en een diepte van zes duimen.  Deze is op zoodanige wijze aan den muur opgehangen, en bevestigd aan de zich aan de linkerzijde bevindende assen, dat het toestel, als men dit wenscht, omgekeerd en aan de achterzijde geopend kan worden, waardoor het inwendige zichtbaar wordt.   Aan den voorkant ziet men een blad van verguld koper dat de geheele voorzijde van den achthoek vormt en bedekt is met spiegelglas; op dat blad zijn de banen der planeten volgens het systeem van Copernicus, maar volgens de proporties van Kepler, aangegeven en geheel uitgesneden, zoodat door die gleuven kleine pinnen rondgaan, met behulp waarvan de bollen der Planeten, tot halve bollen gereduceerd, boven het blad en als het ware op het oppervlak daarvan rondgevoerd worden, waarbij Saturnus vijf, Jupiter vier satellieten met zich voert, en de Aarde   1)  Wij zouden eerder zeggen "in de ruimte" (V.).

[ 385 ]

[ Lat. ]

één (welke onze Maan is).  Deze satellieten zijn daarbij geplaatst op dezelfde schijfjes als de lichaampjes der Planeten.  Ik heb namelijk ook aan de overige Planeten die geen manen hebben, toch zulke schijfjes gegeven die den omringenden aether moeten aangeven en tevens dienen om de Planeten beter zichtbaar te maken.   Alle primaire Planeten 1), welke, behalve de reeds genoemde, Mars, Venus en Mercurius zijn, voeren nu zoo gestadig hun bewegingen rondom de onbewegelijke Zon uit, dat zij niet alleen de periodieke tijden nauwkeurig in acht nemen, maar ook de wetten der snelheidsverandering.  Rondom de Aarde volbrengt de Maan maandelijksche kringloopen.  Bij de satellieten van Saturnus en Jupiter evenwel was het niet mogelijk hetzelfde tot stand te brengen; zoowel wegens de kleine afmetingen van het toestel als ook om het werk niet te lang te laten duren.  Deze zitten daarom vast op slechts één cirkeltje waarvan de primaire Planeet het middelpunt inneemt.

[Tab. 1, fig. 1.] [IMSS]

Voorts omvat de cirkel der Ecliptica, verdeeld in hare 12 teekenen en in 360 graden, alle Planetenbanen.  De schijnbare plaatsen dezer hemellichamen ten opzichte van de Ecliptica worden het gemakkelijkst op de volgende wijze onderzocht: wanneer men de plaats van een Planeet door hare zoogenaamde lengte wenscht te bepalen, dan is het voldoende een draad te spannen van de Aarde naar die Planeet en een tweede daarmee evenwijdig vanuit het middelpunt der Zon, dat onbewegelijk blijft, tot aan den verdeelden cirkel der Ecliptica; deze draad zal dan de lengte der Planeet doen kennen.  Maar ditzelfde kan ook bereikt worden met behulp van een dradenparallelogram, bestaande uit twee gelijke staafjes, die twee daarin bevestigde eveneens gelijke draden hebben, terwijl het deksel van spiegelglas, dat wij hooger genoemd hebben, gesloten blijft.  Immers, men plaatst het parallelogram daarop en terwijl het oog, dat er op neerziet, onbewegelijk blijft wordt het zoo gesteld, dat terwijl de ééne draad over de middelpunten van Aarde en Planeet loopt, de andere over de Zon heengaat, welke tweede draad dan tevens op den Ecliptica-cirkel de plaats der Planeet volgens de lengte zal aangeven.  Hoe men de breedte kan leeren kennen, zullen wij later zeggen, nadat wij het trekken van cirkels tot dat doel zullen hebben geleerd.   In de onderste helft der plaat, tusschen de banen van Saturnus en Jupiter, bevinden zich twee openingen op kleinen afstand van elkander, beide twee duimen lang en een halve duim breed; inde bovenste daarvan verschijnt de dag der maand, in de andere het jaar onzer jaartelling, evenals het overige voortschuivende in hunne cirkelbanen en automatisch ronddraaiend; van deze cirkels heeft de eene [3 maal]*) 365 gelijke dagbogen en de andere een verdeeling in drie honderd jaren 2).  Wat de beweging betreft, deze gaat uit van een ingesloten uurwerk, hetwelk tevens de uren en   1)  Hier verwijst Huygens naar Tab. 1 Fig. 1. (Deze verwijzingen naar de figuren zijn kantteekeningen).   [ *)  OC XXI, 596, n8: "De Volder en Fullenius hebben ten onrechte het woordje 'ter' weggelaten". Vgl. de figuurtjes Q en R op p. 389.]   2)  Huygens verwijst naar Tab. 3, Fig. 4.

[ 386 ]

[ Lat. ]

minuten aangeeft in een halfcirkelvormige opening die ingesneden is in het bovenste gedeelte tusschen de banen van Jupiter en Mars. Immers, terwijl dat getal van ieder uur daarin in de juiste volgorde voorbijschuift, geeft het getal 1) tegelijkertijd de minuten aan.   1)  Door zijn stand in den halven cirkel.

Ook met de hand kan men de geheele machinerie in beweging brengen, als men òf om dat schouwspel gade te slaan de draaiingen der Planeten in een korten tijd wil laten plaats hebben, òf naar hare standen

[ 387 ]

[ Lat. ]

vraagt op een gegeven tijdstip in de toekomst of in het verleden.  Dan toch steekt men een handvatsel in de rechterzijde van den achthoek, hetwelk, door een lichte handbeweging rondgedraaid, bij ieder draaiing aan alle Planeten er eene jaarbeweging bijgeeft, of, in tegengestelden zin

gedraaid, ze evenveel naar het verleden terugvoert, zoodat men iederen hemelstand die geweest is of zijn zal kan afbeelden, en wel van honderd jaar vóór den tegenwoordigen tijd tot twee honderd jaar daarna.  En met hetzelfde gemak wordt alles weder tot den tegenwoordigen tijd teruggebracht

[ 388 ]

[ Lat. ]

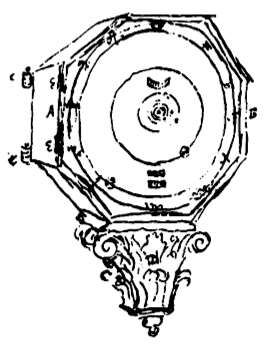
door het draaien van het handvatsel totdat de dag en het uur opnieuw verschijnen in de middelpunten der genoemde openingen.  Als dit volbracht is, moet het handvatsel weggenomen worden, opdat in de automatische beweging alles opnieuw als te voren worde meegevoerd.   Maar opdat het tot dusverre medegedeelde des te duidelijker begrepen worde, voegen wij de afbeelding van het Planetarium, zooals het zich van buiten gezien vertoont, hierbij.

De Automato	Tab: 1
	[IMSS]

VERKLARING   VAN   TAFEL  1,   FIG.  1 VV De Ecliptica verdeeld in 12 teekens en 360°. B De Zon. C De Baan van Mercurius. D Mercurius. E De Baan van Venus. F Venus. G De Baan van de Aarde. H De Aarde met de Maan die om haar draait. I De Baan van Mars. K Mars.

[ 389 ]

[ Lat. ]

L De Baan van Jupiter. M Jupiter met zijne vier satellieten. N De Baan van Saturnus. O Saturnus met zijne vijf satellieten. A.A. Dit zijn de plaatsen van het Apogeum bij de afzonderlijke planeten. Dit geeft de Knoopen aan voor de afzonderlijke Planeten, het eerste figuur den klimmenden, het tweede den dalenden Knoop. PP zijn de breedtecirkels bij de verschillende Planeten. Q wijst de maand van het jaar, en den dag van de maand aan. R wijst het jaar der christelijke jaartelling aan. S wijst de uren aan en de minuten. T teekening, die aanwijst de verhouding der Planeten tot de Zon en onderling, welke fig. 2 nauwkeuriger afbeeldt.

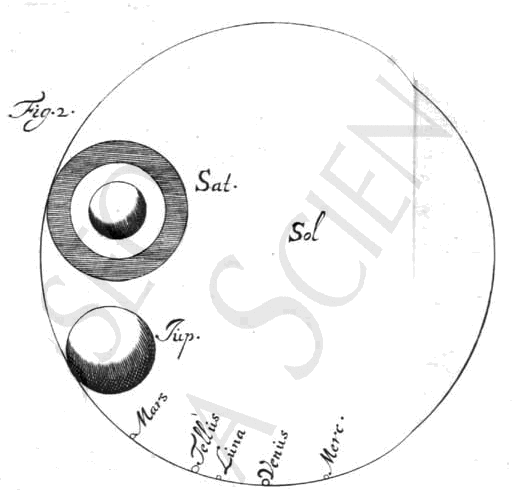
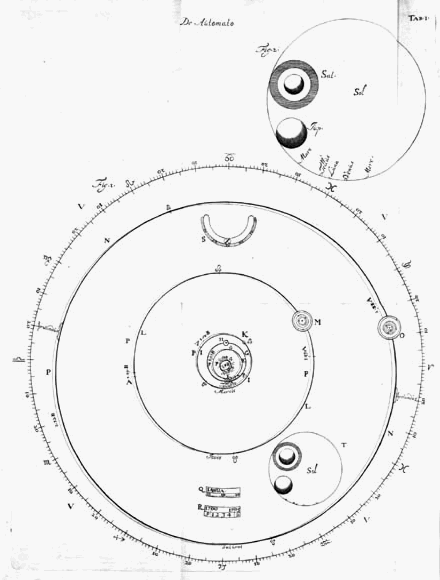
Fig. 2 toont de ware grootte der Zonneschijf in vergelijking met die van alle overige Planeten 1).   Het was niet mogelijk de lichamen van de Zon en de Planeten weer te geven in de ware verhoudingen tot de maat der banen, want dan zouden ze aan alle waarnemingsvermogen ontsnapt zijn door hare kleinheid*); daarom hebben we ze alle afzonderlijk op een ledige plaats der tafel laten afbeelden in de hier bedoelde grootte.   De grootste cirkel zelf stelt dus de Zon voor, de andere de Planeten, die tegen de Zon aan geplaatst zijn opdat zoowel hare onderlinge grootteverhouding, als die ten opzichte van de Zon blijke.   Wat deze verhoudingen betreft, deze zijn opgemaakt uit de vergelijking der afstanden en ook uit die der diameters zooals de telescoop ons die heeft doen zien, zooals uitgelegd is in hetgeen wij lang geleden geschreven hebben over de merkwaardige vormen van Saturnus [^].  Het blijkt dat deze Planetenlichamen in vergelijking met de grootte der Zon veel kleiner zijn dan door de astronomen die ons voorgingen werd geleerd [<].  Dat onder hen de oude sterrekundigen, die de verhoudingen der afmetingen der banen niet kenden en bovendien de middellijnen der Planeten met het bloote oog en zonder eenige zorgvuldigheid maten, zeer ver van de waarheid verwijderd bleven, is geen wonder; maar ook de latere, en zelfs zij die schreven na de uitvinding van den verrekijker,   1)  Zie blz. 410.   [ *)  O.C. XXI, 601: Op het voorblad van het planetarium heeft Huygens laten graveren: Sciendum est ... Vertaling: ] Wetenswaardig is dat, als naar deze grootte van de planeetbanen het overige in werkelijke verhouding weergegeven wordt, de Aarde en de planeten dan alle zo klein zouden zijn dat ze volstrekt niet te zien zouden zijn.  De Zon als een heel klein puntje; en de maanbaan in diameter ongeveer tweemaal zo klein als de zon.  En de banen van de buitenste satellieten van Jupiter en Saturnus niet groter dan dit soort cirkeltjes O O.

[ 390 ]

[ Lat. ]

hebben waarden opgegeven die niet weinig van deze onze maten afwijken.  Ik aarzel niet te verklaren, dat de onze beter zijn, omdat wij ten eerste deze hemellichamen met grooter kijkers hebben waargenomen en ten tweede de middellijnen volgens een secuurder methode hebben gemeten.  De verhouding die hier in de figuur is aangegeven tusschen de Zon en de overige Planeten, is dus zeker, en van de ware verhouding of in het geheel niet of slechts zeer weinig verschillend.  Alleen de verhouding van de grootte der Aarde tot die van de Zon is met mindere zekerheid gevonden; wij hebben deze bepaald door aan te nemen, dat, zooals wat de plaats betreft de Aarde tusschen de Maan [Mars] en Venus ligt, zoo ook hare grootte tusschen die dezer beide hemellichamen inligt; hieruit volgt een afstand van de Zon van ongeveer 12000 aardmiddellijnen, en een verhouding van de middellijn der Aarde tot die van de Zon als van 1 tot 110; welke maten evenwel die zeer fijne waarneming der parallaxen die daarna door de beste astronomen heeft plaats gevonden, waardoor ze den afstand van het Perigeum van Venus hebben berekend, zeer wel bevestigd heeft.   Den aard der beweging nu, die in ons Planetarium wordt gezien leert men kennen door, na omdraaiing van de gehele "doos" de machinerie die er in zit te bekijken 1).  Immers na verwijdering van het deksel die het toestel aan deze zijde afsluit, vertoont zich in het inwendige een koperen plaat, die, evenals de plaat aan de voorzijde, den geheelen achthoek beslaat, van die voorste plaat één duim verwijderd is en een aantal zuiltjes vertoont.  Bovendien vertoont zich hier een 2 voet lange ijzeren as, die dwars zit en evenveel raderen draagt als er Planeten zijn, waarvan elk er aan vastgemaakt is met een door de naaf gaande schroef.  De tanden van deze raderen grijpen in de tanden der grootere raderen, die de afzonderlijke Planeten rondvoeren en tusschen de beide platen liggen.  Bovendien zit op die gemeenschappelijke as nog een ander rad, dat dient tot het in beweging brengen van den cirkel der dagen en maanden, en ook een stuk zoogenaamde schroefdraad zonder einde, dat den cirkel met de verdeeling in 300 jaren in denzelfden tijd eens doet ronddraaien door tusschenkomst van een zeker getand asje.   Wat echter betreft den stand van de ijzeren as, deze is wel horizontaal, maar niet evenwijdig met de groote plaat waarover we reeds gesproken hebben, integendeel wijkt zij aan die zijde welke voor den toeschouwer de rechtsche is, veel verder van de plaat af, hetgeen zoo gemaakt moest worden, opdat de draaiing van één as des te gemakkelijker voldoende zou zijn voor de verschillende bewegingen van al de Planeten.   De aantallen der tanden nu zijn gevonden volgens een zekere methode die wij spoedig zullen uitleggen en zoo nauwkeurig bij de gemiddelde bewegingen aangepast, dat in 20 jaren Saturnus slechts 1' 34" verschoven moet worden, Jupiter 1' 9", Mars 24' 0", Venus 3° 37', Mercurius 7' 47",   1)  Huygens verwijst naar Taf. 2 Fig. 3.

[ 391 ]

[ Lat. ]

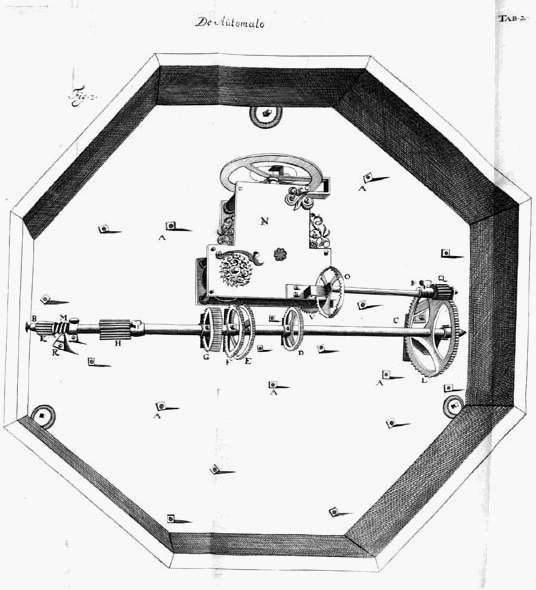
de Maan 1° 31'.  Wij hebben trouwens niet alleen de gemiddelde bewegingen weergegeven, maar de bewegingen met de ongelijkmatigheid die in werkelijkheid bij den loop der Planeten voorkomt, en wel volgens de door Kepler gevonden wetten van snelheidsverandering, welker gezag bij de astronomen zeer groot is.  Op welke wijze deze ongelijkmatigheid verkregen wordt, zullen wij te gepaster plaatse aantoonen.   Verder wordt nog een vanzelf loopend uurwerk aan deze zijde gezien, een weinig boven de as aan de genoemde plaat bevestigd, door de

kracht van hetwelk die groote as jaarlijksche omwentelingen maakt (door welke as dan alles in een gestadige beweging wordt gebracht); immers de beweging gaat van het uurwerk over op een aan de as bevestigd rad [L], waarvan wij gezegd hebben dat het grijpt in den cirkel der dagen en maanden, zooals uit de bijgevoegde figuur duidelijker zal blijken.  Het inwendige van het uurwerk te beschrijven is onnoodig, daar deze uitvinding algemeen bekend is; de bewegende kracht komt, zooals men weet, van een spiraalveer.  In dit geval echter hebben wij de gelijkmatigheid der beweging vergroot door het aanbrengen van een tweede spiraalveer*), welke door haar compenseerende werking de slingeringen kan temperen; welk tweede middel   [ *)  Zie fig. 21 (foto) in XVIII, tegenover p. 525.]

[ 392 ]

[ Lat. ]

wij na de uitvinding der slingers hebben bedacht, en dat weliswaar niet even secuur is, daar door koude en warmte de elasticiteit hare krachten langzamerhand eenigszins vermeerdert of vermindert, maar dat hier geschikter en beter passend is.  De eerste spiraalveer, die de beweging tot stand doet komen, wordt eens in de week opgewonden.

VERKLARING   VAN   TAF.  2,   FIG. 3

A.A. zijn vierkante plaatjes, waarmede de uiteinden der in fig. 4 taf. 3 door de letters T.T. aangegeven zuiltjes vastgeschroefd worden. CB is de twee voet lange ijzeren as. D is het rad, van 121 tanden voorzien, dat de raderen van Mercurius in beweging brengt. E is het rad van Venus, met 52 tanden. F is dat der Aarde, met 60 tanden. G is dat van Mars, met 84 tanden. H dat van Jupiter, met 14 tanden. K dat van Saturnus, met 7 tanden. L een rad met 73 tanden, brengt den cirkel, waarop de dagen en maanden gegrift zijn, in beweging. M is een stuk schroefdraad zonder einde, welks omwenteling den omloop in 300 jaren teweeg brengt met behulp van 2 radertjes, vastgemaakt aan het gemeenschappelijk asje, afgebeeld op Taf. 3 en aangegeven met de letter E, welke elk 6 tanden hebben, en waarvan het eene in die schroefdraad grijpt, het andere, aan de binnenzijde gelegen, in de tanden van het rad der 300 jaren. N is het uurwerk. V is het rad, waardoor het uurwerk de as C.B. beweegt. P zijn 4 tanden aan het uiteinde van de as van het rad V. O is het rad, dat door de tanden P bewogen wordt en 45 tanden heeft. Q is een rad vast zittende aan de as van het rad O, van 9 tanden voorzien, door hetwelk het rad L bewogen wordt, waardoor tevens de as 1) draait. R is een koperen plaatje vastgehecht aan die grootere plaat, in welks kleine opening het getande in tafel 3 afgebeelde radje [E] past.   In de bijgevoegde figuur, die het aanzicht van het achterste voren gekeerde toestel (na verwijdering van het deksel) toont, houden de vierkante plaatjes, waarbij de letter A staat (en de andere daaraan gelijke 2)) de uiteinden der zuiltjes 3) daarop vastgeschroefd, door welke zuiltjes de   1)  Bedoeld is de ijzeren as CB (V).   2)  Waarbij de letter A ontbreekt.   3)  Zuiltje T, zie fig. 4, tab. 3.

[ 393 ]

[ Lat. ]

plaat 1), die hier gezien wordt, is bevestigd aan die andere, zich aan de voorzijde bevindende plaat 2), die door de banen der Planeten in deelen gesneden wordt.   De tweevoetige ijzeren as is CB, aan die zijde waar de letter C staat 2 duimen van de plaat verwijderd.   De aan deze as bevestigde raderen geven de beweging aan de Planetenbanen, D aan die van Mercurius, E aan die van Venus, F aan die der Aarde, G aan die van Mars, H aan die van Jupiter, K aan die van Saturnus.   Het rad L echter beweegt den cirkel waarop de maanden en dagen gegrift zijn, en eindelijk bewerkt de omwenteling der schroefdraad M den omloop in 300 jaren, door tusschenkomst van 2 radertjes, vastgemaakt   1)  Aan de achterkant van de doos waarop de ijzeren as CB is gemonteerd.   2)  De koperen plaat, bestaande uit concentrische ringen.

[ 394 ]

[ Lat. ]

aan een gemeenschappelijk asje, welke elk 6 tanden hebben, en waarvan het eene in die schroefdraad grijpt, het andere, aan de binnenzijde gelegen, in de tanden van het groote jaarrad.   De zoo groote verscheidenheid der bewegingen komt dus tot stand door één as CB, die jaarlijksche omwentelingen maakt (immers zoowel het rad L, als de schroefdraad M zitten daaraan vast); deze as echter wordt op de volgende wijze door het uurwerk in beweging gebracht.  In het uurwerk bevindt zich een rad V, waarvan hier slechts een klein deel wordt gezien, welk rad telkens in 96 uur eenmaal ronddraait.  Aan het eene uiteinde van de as van dit rad zijn 4 tanden aangebracht; deze grijpen in het rad O, dat 45 tanden heeft.  Aan dit rad is op dezelfde as toegevoegd het rad Q, van 9 tanden voorzien, welke ten slotte grijpen in de 73 tanden van het rad L.   Nu is het zaak ook de Planeetraderen, die zich tusschen beide platen bevinden zichtbaar te maken, opdat het blijke hoe zij geconstrueerd zijn en hoe ze rondloopen.

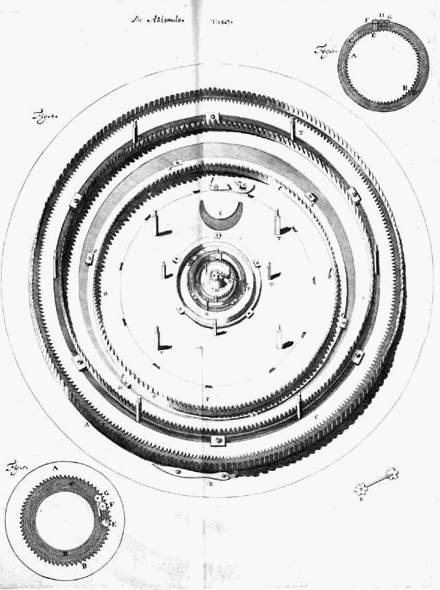
Fig. 4.	De Automato.   Tab. 3.	Fig. 6.
Fig. 5.		E

A is het rad van Saturnus, met 206 tanden. B is het armpje waar Saturnus op vast zit. C is het rad waarop de 300 jaren gegrift zijn, opdat het steeds het jaar aangeve, in dien langen tijd eenmaal ronddraaiende. Het is voorzien van 300 tanden. Het draait met behulp van de schroefdraad zonder einde, welke in Taf. 2, fig. 3 met de letter M is aangeduid, en dat door middel van het getande asje E. D is het rad dat de maand en den dag der maand door zijn omwenteling doet kennen; het is voorzien van 219 tanden.  [ E. Getand asje, zie C. ] F is het rad dat den op het armpje G bevestigden Jupiter rondvoert; het heeft 166 tanden.  [ G. Armpje, zie F. ] H is het rad van Mars met bijbehoorend armpje, voorzien van 158 tanden. I is het rad der Aarde tezamen met de Maan, hetwelk 60 tanden heeft. K is een getande cirkel, die vast zit aan de voorplaat van het geheele toestel en die, terwijl het Aarde-rad ronddraait, de radertjes beweegt, waarop Aarde en Maan gezamenlijk bevestigd zijn. Het heeft 137 tanden. L is het rad van Venus, voorzien van 32 tanden. M is het rad van Mercurius, dat 17 tanden heeft. N is een vaste as, aan welker eene uiteinde de Zon bevestigd is.

[ 395 ]

[ Lat. ]

O is het asje van Mercurius, aan de eene zijde bevestigd aan de as der Zon, aan de andere zijde aan het zuiltje P dat vast zit in de onbewegelijke plaat der Aarde. Dit asje draagt 2 radertjes, waarvan het eene R, dat het rad van Mercurius in beweging brengt, 7 tanden heeft, en het andere Q 12 tanden. Dit asje is zoover boven het vlak dezer figuur verheven, dat de raderen van Venus en Mercurius daaronder hunne bewegingen kunnen volvoeren.  [ PQR. Zie O. ] S is de opening waar de plaat die de uren aangeeft langs rond loopt. T.T.T.T duiden zuiltjes aan waarmede al deze dingen, met behulp van schroeven vastgehecht zijn aan die plaat die figuur 3 van Tafel 2 voorstelt. a b is een platte ring, waarop een Planeet wordt rondgevoerd. c d is een staande ring met tanden voorzien. e e zijn pinnen die den platten ring bij het rondloopen in bedwang houden. l m is een armpje.  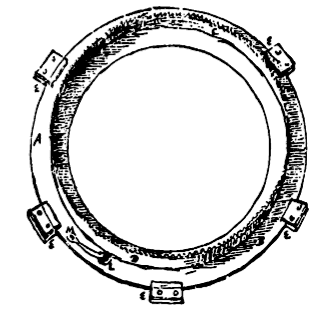[ m: asje, l: buisje.]   Bij elke planeet behoort dus een platte ring overeenkomende met den omvang van haar baan, waar een staande getande ring, die er een rechten hoek mede maakt, aan vast zit, zich overal even hoog boven den omtrek van den eersten ring verheffend.  Die eerste ring, van binnen zich aansluitende bij de voorste achthoekige plaat, voert het bolletje dat het lichaam der Planeet voorstelt met zich rond, hetwelk met een klein pinnetje daarop vastzit, waardoor het aan de buitenzijde der voorste plaat een weinig uitsteekt.  Aan den omtrek van dezen ring zijn zekere pinnen geplaatst, die vastgemaakt zijn aan de plaat, tusschen welke pinnen de ringen hun cirkelvormige bewegingen uitvoeren, terwijl ze tevens door die pinnen verhinderd worden zich van de genoemde plaat te verwijderen.  Van die pinnen zijn er bij de bovenplaneten Saturnus en Jupiter elk 5 of 6 gevoegd wegens de grootte der ringen, bij elk der overige zijn 4 of 3 pinnen voldoende.

[ 396 ]

[ Lat. ]

ring a b zelf, maar aan het armpje l m, dat er aan vast zit en dat bewegelijk is om het asje m; in l draagt dit armpje de Planeet die in een buisje vastgehecht is; hier moet dan de ring met een wijder opening doorboord worden, zoo toch zal de Planeet gemakkelijk door een elliptische gleuf voortbewogen worden.  Maar daar die ellipsen zoo weinig van cirkels verschillen, scheen er geen voldoende reden te zijn om ellipsen te gebruiken.  Bij Saturnus en Jupiter hebben wij echter op deze zelfde manier bereikt dat ze zich vrijer door de vrij smalle cirkelgleuven kunnen bewegen.  Geheel daaraan gelijk is nu ook de cirkel waarop de dagverdeelingen gegrift zijn; maar de jaarcirkel heeft alleen een platten ring met getanden omtrek; hoe deze in beweging gebracht wordt is reeds vroeger gezegd [p. 393-4].  En voor dezen dagcirkel en jaarcirkel is een plaats gevonden tusschen de cirkels die de Planeten Saturnus en Jupiter dragen, en daarom zijn ook de openingen, waardoor die indeelingen gezien moeten worden, tusschen de banen van die Planeten in de voorste plaat uitgesneden.

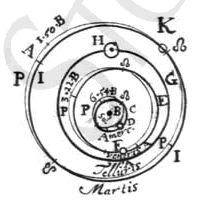
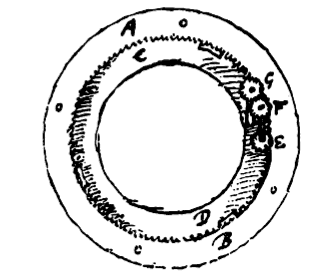
Nu moeten we laten zien 1) hoe de maandelijksche beweging der Maan is ingericht.  Aan de binnenzijde van het stuk van de Planetenplaat dat ligt tusschen de banen van Mars en de Aarde, is een ring vastgehecht, die in zijn binnenrand 137 tanden heeft, welken ring in deze figuur de daarin geschreven letters A B aanduiden.  Deze getande ring is een weinig grooter dan de jaarlijksche kringloop der Aarde, en de ring AB is ook een weinig verheven boven het vlak waar hij aan vast zit, zoodat daaronder de pinnen geplaatst kunnen worden tusschen welke de ring die de Aarde draagt ronddraait, welke ring is aangeduid door de letters C D.  Deze ring draagt voorts een asje met zich mede, dat er loodrecht op staat en dat aan beide uiteinden daaraan vastgemaakte radertjes draagt, E en F, waarvan het onderste 12 tanden heeft die grijpen in de tanden van den ring AB, en het bovenste 13.  De tanden van het bovenste grijpen in de 12 tanden van het radje G, dat er naast geplaatst is en dat evenzoo een aan den cirkel CD vastgehechte as heeft; welke as een holte heeft die geopend is naar de voorzijde der Planetenplaat, in welke holte een klein met het Maancirkeltje verbonden staafje is vastgehecht.  Ik heb nóch een zeker aan den cirkel CD vastgemaakt stukje af laten beelden dat de genoemde asjes van boven in bedwang houdt, nóch het staande getande rad, opdat niets het gezicht op de radertjes E en F zou belemmeren.   Wanneer dus de Aardring ronddraait in de richting aangegeven door de letters A E B, welke omwenteling gezien aan de voorzijde der plaat geschiedt volgens de orde der teekenen van den Dierenriem, dan moeten noodzakelijk de radertjes E en F in tegengestelde richting draaien, en het radje G weder in de daaraan tegengestelde richting, dat is in dezelfde richting als de Aardring.  We hebben reeds gezegd dat in de holle as van het radje G een pin gestoken is, waarmede een ringetje verbonden   1)  Zie tafel 3, fig. 5.  [Figuur toegevoegd uit O.C. XXI, 616.]

[ 397 ]

[ Lat. ]

is, dat de Maan op zijn omtrek draagt en de Aarde in zijn middelpunt; hierdoor is de omloop der Maan juis geregeld; hoe nauwkeurig hij met den waren duur der maandperiode overeenkomt zal later blijken.   Na tot zoover de afzonderlijke deelen van het toestel te hebben verklaard, zullen wij nu zeggen met welke verhoudingen der stralen en met welke middelpunten wij de loopbanen der Planeten op de voorste plaat beschreven hebben, evenzoo waar wij de punten der Aphelia en der Knoopen geplaatst hebben; ten slotte welk aantal tanden wij aan elk rad toegekend hebben opdat het met een gemiddelde beweging uit zou komen en volgens welke methode die aantallen bepaald worden; en eindelijk door welke constructie der tanden wij de vereischte ongelijkmatigheid der bewegingen verkregen hebben.   Wij hebben dan, na aan de achthoekige plaat een zoodanige grootte gegeven te hebben, dat de loodlijn die uit het middelpunt op een zijde wordt neergelaten 11½ duim lang is, vanuit het zelfde middelpunt waar ook de Zon geplaatst is, den cirkel der teekenen van den Dierenriem beschreven met een straal van 10 2/3  duim 1).  Dezen cirkel hebben wij verdeeld in 360 deelen en de namen der 12 teekenen er op de juiste plaatsen bijgeschreven, het Teeken van den Ram plaatsende aan de zijde die voor den toeschouwer de rechtsche is, op gelijke hoogte met het middelpunt.

[Tab. 1, fig. 1.]	[IMSS]

Voorts zijn de plaatsen der Aphelia in een bijgevoegde tabel aangegeven; deze geeft dus tevens aan naar welke zijde het middelpunt van iedere Planetenbaan is genomen.  En uit de verhouding der stralen die er naast is geplaatst, leert men ook de grootte dezer lijnen kennen, indien er één daarvan, namelijk de straal der Aardbaan, bepaald is, aan welken wij de lengte van 1 duim hebben gegeven, d. i. een twaalfde deel van een Rijnlandschen Voet; deze straal wordt geacht in 100000 deelen verdeeld te zijn en de stralen der overige Planetenbanen hebben zooveel van die deelen als in de tabel is aangegeven.  In diezelfde eenheden zijn daar de excentriciteiten aangegeven; men moet deze begrijpen als getrokken uit het middelpunt der Ecliptica, waar de plaats der Zon is, naar de plaatsen der Aphelia, en aldaar het middelpunt van iedere baan plaatsen.   Wanneer ik b.v. de baan van Saturnus wil aangeven in het begin van het jaar 1682 der Christelijke Jaartelling, dan trek ik een lijn uit het middelpunt der ecliptica naar den 27-sten graad, 40-sten minuut van den Schutter; op de lijn zet ik vanuit hetzelfde middelpunt 54 deelen af van zoodanige grootte dat de Aardbaanstraal of 1 duim er 100 bevat; immers wij kunnen bij deze kleine afmetingen de verdere kleine deeltjes niet tot hun recht doen komen.  Zoo vind ik het middelpunt van de baan van Saturnus.  Dan beschrijf ik, tot straal nemende een lengte van 951 zoodanige deelen, de baan der Planeet, welker Aphelium ik aanduid met de   1)  Zie tafel 1, fig. 1.

[ 398 ]

[ Lat. ]

letter A, daar waar ze die rechte lijn snijdt, waarvan ik aangegeven heb, dat ze uit het middelpunt getrokken is.  Daar echter de Planeetbanen in den hemel alle een kleinen hoek maken met het vlak der Ecliptica, anders gezegd met het vlak der Aardbaan, hetwelk hier ondersteld wordt het oppervlak der plaat zelve te zijn, zoo is het duidelijk dat, aangezien die banen met haar eene helft boven dat vlak liggen en met de andere helft er onder, het niet de Planeetbanen zelve zijn die door ons zijn geconstrueerd, maar zoodanige lijnen dat daarop vallen de voetpunten der loodlijnen die uit willekeurige punten der banen op het vlak der Ecliptica zijn neergelaten. — korter: maar de loodrechte projecties dier banen op het vlak der Ecliptica —, welke lijnen wij echter als de banen zelve beschouwen, omdat volgens die lijnen de beweging der Planeet in de lengte wordt onderzocht; in werkelijkheid echter zijn het de banen op het vlak der Ecliptica geprojecteerd.   Wij hebben derhalve de 2 punten volgens welke iedere baan het vlak der Ecliptica snijdt (deze worden Knoopen genoemd) met de daarbij passende teekens en aangeduid, waarvan wij het eerste aan den klimmenden Knoop hebben toegekend, vanwaar af n.l. de Planeet zich naar de Noordzijde der Ecliptica beweegt, welke men zich boven de plaat moet denken, en het tweede aan den dalenden Knoop, na het voorbijgaan waarvan de Planeet overgaat naar de Zuidelijke helft.  Deze twee teekens nemen tegenover elkander liggende plaatsen 1) in op een door het middelpunt der Zon getrokken rechte lijn volgens het algemeen door de sterrekundigen aangenomene, hoewel dit toch niet volstrekt nauwkeurig schijnt te zijn [J.d.S.], zooals te gelegener plaatsen nader verklaard zal worden.  Wij hebben verder de plaatsen der klimmende Knoopen en de hoeken die de vlakken der Planeetbanen maken met het vlak der Ecliptica hier in de tabel aangegeven, die schrijvers volgend, die ons het meest geloofwaardig voorkomen, bij Venus en Mercurius met gebruikmaking van de waarnemingen der allernieuwste auteurs, bij gelegenheid waarvan deze Planeten zich vóór de Zon zelve vertoonden. 1 Januari 1682   *) Aphelia. Klimmende Knoopen Hellingen  Planeet-  baan- stralen  Excentrici-  teiten in dezelfde eenheden van Mercurius  15° 11' 19"   14° 29' 47"   6° 54' 0"  38806  8149       ,,  Venus 2° 59' 44"   13° 54' 52"   3° 22' 0"  72400  500       ,,  Mars 0° 30' 17"   17° 38' 12"   1° 50' 30"  152350  14115       ,,  de Aarde 7° 7' 20"   100000  1800       ,,  Jupiter 7° 55' 43"   5° 30' 42"   1° 19' 20"  519650  25058       ,,  Saturnus 27° 39' 46"   21° 36' 26"   2° 32' 0"   951000  54207       1)  Zie tafel 1, fig. 1.   [ *)  De waarden zijn ontleend aan Kepler, Tabulae Rudolphinae (1627), behalve die van de klimmende knoop van Mercurius. Zie O.C. XXI, p. 148-9, 177, JdSç, 20 dec. 1677: Gallet.]

[ 399 ]

[ Lat. ]

De diameter van den ring van Saturnus staat tot de middellijn der Zon als   11  : 37  *) De diameter van den ring van Saturnus staat tot de middellijn van den bol van Saturnus als 9  : 4 De diameter van Jupiter staat tot de middellijn der Zon als   2  : 11 ,, Mars ,, 1  :  166 ,, Aarde ,, 1  :  110 ,, Venus ,, 1  : 84 ,, Mercurius ,, 1  :  308  1)   Opdat men de schijnbare breedten der Planeten kunne leeren kennen, hebben wij aan beide zijden op de rechte lijn die de tegenover elkander liggende Knoopen verbindt, cirkelbogen beschreven, den eenen aan de buitenzijde van de Noordelijke helft der baan, den anderen binnen de Zuidelijke helft, welke bogen van deze baangedeelten, daar waar de onderlinge afstand het grootst is zoover verwijderd zijn als de baan zelve op die plaatsen boven en onder het vlak der Ecliptica moest liggen; en terzelfder plaatse hebben wij er de hellingshoeken bijgeschreven.  Wanneer echter de Planeet zich in een willekeurig punt van de geprojecteerde baan bevindt, dan zal, als men den kleinsten afstand neemt van dat punt tot den daarbij gelegen boog, deze met groote benadering den afstand aangeven, waarop aldaar de ware baan der Planeet van het vlak der Ecliptica verwijderd is; en indien men dit interval met den afstand der Planeet tot de Aarde vergelijkt, dan zal ook de breedtehoek gemakkelijk volgens de leer der driehoeksmeting berekend kunnen worden.  Laat het voldoende wezen dit gezegd te hebben over den uitwendigen vorm van het Planetarium en over het gebruik dat men er van maken kan; gaan wij nu over tot de samenstelling van het inwendige.   Het aantal tanden op de raderen is op de volgende wijze door ons gevonden.  De gemiddelde jaarlijksche beweging van elke Planeet onder den Dierenriem, d.i. de beweging in 365 dagen, hebben wij vergeleken met de gemiddelde jaarlijksche beweging der Aarde, zooals deze bewegingen in de astronomische tafels te vinden zijn, en wel met herleiding hunner geheele baanbewegingen tot zestigste deelen van seconden. Daar de zoo gevonden getallen dezelfde verhouding tot elkander hebben als de cirkelbogen die in denzelfden tijd door de Planeet en door de Aarde in hare banen worden beschreven, zoo volgt er uit, dat de omlooptijden van die beide tot elkander in de omgekeerde verhouding staan; welke verhouding, of een dergelijke door kleinere getallen uitgedrukte, dus ook de aantallen der tanden tot elkander moeten hebben; van de tanden namelijk waarmede eenerzijds het Planetenrad, anderzijds het daarin grijpende op de groote as geplaatste rad moeten worden voorzien; immers   [ *)  Deze verhoudingen komen overeen met die in Systema Saturnium (1659),  Ned.]   1)  Zie blz 410.

[ 400 ]

[ Lat. ]

door iedere omwenteling van deze as doorloopt de Aarde haar geheele baan, omdat wij een gelijk aantal tanden aanbrengen bij het rad dat de Aarde draagt en bij het rad dat daarmede op de groote as overeenkomt, b.v. 60 of een ander willekeurig getal dat voor die raderen past.   De geheele kwestie komt dus hierop neer: wanneer twee groote getallen gegeven zijn die in een bepaalde verhouding tot elkander staan, andere kleinere te vinden voor de radertanden die niet ongeschikt zijn door hun grootte en die dezelfde verhouding met een zoo groote nauwkeurigheid opleveren, dat geen andere kleinere getallen een betere benadering geven.  Maar door een voorbeeld zullen wij deze geheele zaak beter duidelijk maken.  Stel dus dat gevonden moeten worden de tanden op het rad van Saturnus en die op het kleinere rad dat dit in beweging brengt, hetwelk bevestigd is aan de groote as, welk laatste rad, zooals hooger gezegd, is aangeduid door de letter K 1).   Voor de jaarlijksche beweging van Saturnus (ik volg hierbij, zooals in het overige, de allernieuwste tafels van Riccioli) wordt opgegeven 12° 13' 34" 18"'.  Voor de jaarlijksche beweging der Aarde, die hij de beweging der Zon noemt, 359° 45' 40" 31"'.*)  Wanneer wij alles tot zestigste deelen van een seconde herleiden, wordt dus de verhouding 2640858 : 77708431.   Zooals het laatste dezer getallen staat tot het eerste, zoo verhoudt zich dus de omlooptijd van Saturnus tot den tijd waarin de Aarde om de Zon draait; bijgevolg moet het getal der tanden van het Saturnusrad zoo nauwkeurig mogelijk in deze verhouding staan tot het aantal tanden van het rad dat het in beweging brengt.  Om nu kleinere getallen te vinden die deze verhouding ongeveer uitdrukken, deel ik het grootste getal door het kleinste en dan het kleinste door de rest, en deze laatste opnieuw door de rest der vorige deeling°); en zoo al voortgaande vind ik dat de eerste deeling oplevert 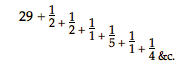  Ik vind namelijk een getal met een daarbij behoorende breuk, waarvan de teller 1 is, maar waarvan de noemer opnieuw een breuk met zich voert, waarvan de teller 1 is, terwijl de noemer alweer is samengesteld als de vorige; en zoo maar voort; op welken weg voortgaande zoover als   1)  Zie tafel 2, fig. 3. [<]   [ *)  Astronomia reformata, Lib.I, cap. IV;  OC XXI, p. 179;  Almagestum novum.]   [ °)  Bij de ontwikkeling van de theorie van de kettingbreuk (continued fraction, fraction continue) was Huygens één van de eersten, na John Wallis, Arithmetica infinitorum, 1656, p. 182.]

[ 401 ]

[ Lat. ]

men kan, men ten slotte hiertoe komt, dat bij de deeling een rest 1 overblijft.   Als men nu van deze breukenreeks de laatste breuken, vanaf een willekeurig gekozen breuk, weglaat, b.v. hier de breuk 1/5 met de daarop volgende, en de overige met het daaraan voorafgaande getal tot een gemeenschappelijken noemer herleidt, dan zal de verhouding van dien noemer tot den teller niet veel verschillen van de verhouding van het kleinste der gegeven getallen tot het grootste.  Zóó gering zal het verschil zijn, dat het niet mogelijk is met kleinere getallen dichter tot de ware verhouding te naderen.  De methode der herleiding is eenvoudig; immers de laatste hier beschouwde breuken , hebben de waarde 1/3; vandaar voortgaande tot de voorafgaande breuk, vinden we door herleiding = 3/7; daarna ook het geheele getal er bij nemende, vinden we door herleiding 29 + 3/7 = 206/7.  De verhouding der getallen 7 en 206 komt dus nagenoeg overeen met die der getallen 2640858 en 77708431.  Daarom hebben wij aan het rad van Saturnus 206 tanden gegeven, en aan het rad dat eerstgenoemd rad in beweging brengt 7 tanden.  Wat betreft onze bewering, dat er geen kleinere getallen te vinden zijn, die de gegeven verhouding beter weergeven, dit zullen we als volgt bewijzen.  Vooreerst is het zeker dat de op deze wijze door herleiding verkregen getallen onderling ondeelbaar zijn, volgens stelling 1 van boek 7 der Elementen 1), aangezien onze gedurige deeling niets anders is dan een zoodanige Euclidische aftrekking; indien men deze laatste toepast op onze getallen 206 en 7, door herleiding verkregen, dan is het duidelijk, dat ten slotte de eenheid overblijft, omdat de teller van al die breuken de eenheid is.  Indien er nu twee andere getallen zijn welker verhouding dichter nadert tot die der groote getallen, dan is het noodzakelijk dat deze, wanneer men voortdurend het grootste door het kleinste deelt totdat de eenheid overblijft, het quotient 29 opleveren, met dezelfde bovengenoemde breuken er telkens bijgevoegd, waarbij men evenwel verder voortgaan moet dan tot die breuken vanwaar wij bij onze herleiding zijn begonnen toen wij de getallen 7 en 206 vonden.  Op andere wijze toch is het onmogelijk dichter te naderen tot het quotient der eerste deeling dat alle genoemde breuken, to het einde toe uitgedeeld, omvat.  Zoo zou het, omdat bij voortdurende deeling van 206 door 7 wordt gevonden ,   1)  Euclides VII Stelling 1:  "Als twee ongelijke geheele getallen gegeven zijn en het kleinste voortdurend beurtelings van het grootste afgetrokken wordt, dan zullen, als de rest nooit opgaat op de voorafgaande rest, zoodat tenslotte de eenheid overblijft, de gegeven getallen onderling ondeelbaar zijn". (V.).

[ 402 ]

[ Lat. ]

noodzakelijk zijn, dat door een dergelijke deeling der een betere benadering opleverende getallen, althans één breuk aan de reeds genoemde breuken werd toegevoegd, hetzij 1/5 of een andere, waardoor wij dichter tot het algemeene quotient zouden naderen dan door bij 1/1 af te breken.  Hieruit echter is het duidelijk dat, als wij de herleiding uitgevoerd hebben, grootere getallen verkregen worden, dan indien wij met een vroegere breuk begonnen waren, aangezien door de toevoeging van iedere herleide breuk een breuk ontstaat bestaande uit onderling ondeelbare getallen en die derhalve niet tot kleinere getallen herleid kan worden; hetgeen den onderzoeker duidelijk zal worden als hij zijn aandacht zal geschonken hebben aan de volgende zeer gemakkelijk te bewijzen stelling:  als gegeven zijn 2 onderling ondeelbare getallen, dan zal elk daarvan ondeelbaar zijn ten opzichte van zichzelf of een veelvoud van zichzelf, vermeerderd met het andere getal.  Immers indien dit niet het geval is, dan zal het oorspronkelijk getal een gemeenen deeler hebben met die som; het heeft echter ook een gemeenen deeler met een deel daarvan, namelijk met zichzelf of zijn veelvoud; derhalve heeft het ook een gemeenen deeler met de rest, hetgeen ongerijmd is, daar de twee getallen onderling ondeelbaar werden ondersteld.  Derhalve zullen de getallen die dichter naderen tot de gegeven verhouding niet kleiner maar grooter zijn dan de gevonden getallen 206 en 7.   Voorts begrijpt men gemakkelijk, dat de herleiding der breuken steeds het nuttigst begonnen wordt met een breuk, waarop er een volgt die een grooter noemer heeft dan de aangrenzende; daarom zijn wij dan ook in het vorige voorbeeld met de herleiding begonnen daar waar de breuk 1/5 volgde.   Het nut dezer methode strekt zich uit tot vele andere gevallen wanneer het er op aankomt een zekere door getallen gegeven verhouding te herleiden tot een ongeveer gelijke door andere kleinere getallen uitgedrukte verhouding.  B.v. wanneer de verhouding van den cirkelomtrek tot de middellijn in een groot aantal juiste cijfers gegeven wordt, n.l.  31415926535 : 10000000000.  Door uitvoering der deeling verkrijgt men in dit geval*) 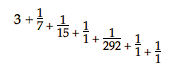terwijl, indien wij de herleiding beginnen met de breuk 1/7, de Archimedische verhouding 22 : 7 ontstaat, indien wij echter met 1/1 beginnen, dan ontstaat een andere veel nadere waarde, die door Adr. Metius   [ *)  Zie ook OC XX, p. 394.]

[ 403 ]

[ Lat. ]

bekend is gemaakt, n.l. 355 : 113; immers 113 : 355 = 10000000 : 31415929, enz.  Op dezelfde wijze kan men andere de waarheid nog dichter benaderende verhoudingen vinden, maar deze Metiaanse verhouding is voor het gebruik geschikt en munt uit door de kleinheid der getallen, vanwege de kleinheid der breuk 1/292, die volgt op de breuk waarmede de herleiding begonnen is.  Iets dergelijks vindt men niet licht terug als men het met andere getallen probeert.  Bovendien moet men weten, dat door deze onze herleiding afwisselend een grootere en een kleinere waarde dan de juiste gevonden wordt, een grootere n.l. als de herleiding begonnen is met de eerste, derde, vijfde, of een verdere oneven breuk.  Wanneer wij b.v. de laatstvermelde herleiding beginnen met de derde breuk, die 1/1 is, dan wordt de verhouding van den cirkelomtrek tot de middellijn 355 : 113 grooter dan de ware waarde, maar indien ik begonnen was met het tweede, d.i. met 1/15 dan zou de verhouding 333 : 106 ontstaan zijn, die kleiner is dan de ware waarde; indien men echter een begin maakt met de eerste die 1/7 is, dan ontstaat de Archimedische verhouding 22 : 7 die grooter is dan de ware; ware verhouding noem ik hier de verhouding die uitgedrukt wordt door de genoemde groote getallen, welke wij immers als de verhouding zelve van cirkelomtrek tot diameter hebben aangenomen.  Het bewijs hiervan berust op dit zeer bekende fundament, dat iedere breuk kleiner wordt als de noemer vermeerderd wordt, en grooter als deze verminderd wordt.   Laat n.l. het getal dat door de eerste deeling ontstaan is A zijn terwijl er overigens een willekeurig aantal afdalende breuken B C D E F zijn en aan den noemer van de onderste F een breuk toegevoegd is, die uit de herleiding van al de overige breuken kan worden verkregen en Z heet.  Daar dus de breuk die F heet grooter is dan de ware breuk, daar zij een noemer heeft die kleiner is dan de ware noemer die 1 + Z zou zijn, zoo ontstaat hieruit door vermeerdering van den noemer van breuk E met breuk F een uit de breuken E en F herleide breuk die kleiner is dan de ware waarde, en daarom zal dan weer door vermeerdering van den noemer der breuk D, als de herleiding daarvan heeft plaats gehad, een breuk uit D, E en F door herleiding gevonden ontstaan die grooter is dan de ware waarde, en eindelijk door vermeerdering van den noemer van breuk C een laatste breuk, uit de herleiding der breuken C, D, E en F ontstaan, die kleiner is dan de ware.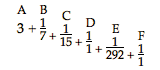

[ 404 ]

[ Lat. ]

Daar dus noodzakelijk de breuken die ontstaan uit de herleiding der omhoog loopende reeks van breuken afwisselend nu grooter dan kleiner dan de ware breuken worden, en de onderste waarmede men een begin maakt, altijd grooter is dan de ware waarde, zoo blijkt het gemakkelijk dat, zoo deze een oneven plaats inneemt, ook de breuk die uit de herleiding van alle breuken ontstaat, grooter dan de ware waarde zal zijn, en dus ook gevoegd bij het getal A een verhouding zal opleveren die grooter is dan de ware.  Maar indien die breuk waarmede een begin gemaakt wordt, een even plaats inneemt, zoo is het duidelijk, dat uit de herleiding van al de breuken een breuk ontstaan zal die kleiner is dan de ware waarde en dus ook, gevoegd bij het getal A, een verhouding zal opleveren die kleiner is dan de ware.  De waarheid der stelling is dus gebleken.  Men moet verder weten dat, indien men in volgorde alle benaderde waarden behoorende bij de gegeven verhouding wenscht te verkrijgen, men dan zowel met alle breuken die een oneven plaats innemen als ook met alle die een even plaats innemen de herleiding moet maken*), en dat wel met dien verstande dat men voor elken noemer die grooter is dan 1 afzonderlijk alle mogelijke noemers in de plaats stelt van af de eenheid tot aan den waren noemer [ad illum: tot aan die noemer] en met elk daarvan de herleiding opnieuw begint en uitvoert.  Immers, indien dit geschiedt met de breuken die op oneven plaatsen staan, zullen alle waarden die grooter zijn dan de ware in volgorde ontstaan, maar indien dit geschiedt met de breuken der even plaatsen, zullen in volgorde alle waarden verkregen worden die kleiner zijn dan de ware.  Indien wij b.v. in het hooger gegeven voorbeeld de eerste breuk 1/7 achtereenvolgens vervangen door 1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, zullen daaruit na herleiding de volgende verhoudingen ontstaan die alle grooter zijn dan de ware:  4 : 1, 7 : 2, 10 : 3, 13 : 4, 16 : 5, 19 : 6, 22 : 7.  Vervolgens beginnende bij de derde breuk D, zal de volgende grootere verhouding worden 355 : 113.  En als wij beginnen met de vijfde F, wordt de daarop volgende grootere verhouding 104348 : 33215.  Indien aan den anderen kant voor de tweede breuk 1/15 achtereenvolgens in de plaats gesteld wordt 1/1, 1/2, 1/3 enz. en evenzoo voor de vierde 1/292 alle breuken in de plaats gesteld worden van de eenheid af, dus 1/1, 1/2, 1/3 tot en met 1/292, dan zullen wij, na uitvoering der herleidingen,in volgorde de verhoudingen hebben die kleiner zijn dan de ware, ten minste diegene die verkregen kunnen worden als men een begin maakt met de breuk E.  Indien wij eindelijk een volledige gemengde serie willen hebben van waarden die of een grootere of een kleinere dan de ware verhouding aangeven, waarvan elke dichter bij de ware verhouding komt dan de vorige, dan moet men deze regel in acht nemen dat men bij elke breuk, waarvan de noemer grooter dan de eenheid is, niet, zooals zooeven werd gedaan, alle kleinere noemers er in zet van de eenheid af, maar dat men dan beginnen moet met het kleinste getal dat de helft van dien noemer overtreft.   [ *)  In de originele vertaling alleen: "men ook met alle breuken die een oneven plaats innemen".]

[ 405 ]

[ Lat. ]

Deze methode ook bij de overige Planeten volgende, hebben we aan het rad van Jupiter 166 tanden gegeven, aan het rad hetwelk dit rad in beweging brengt 14 tanden, aan het rad van Mars 158 tanden, aan het rad dat dit rad beweegt 84 tanden.  Aan het rad van Venus 32 tanden, aan het rad dat dit in beweging brengt 52 tanden; welke getallen zich ongeveer verhouden als 43 : 70.  Indien wij deze laatste getallen hadden gebruikt, en dus aan het rad van Venus 43 tanden hadden gegeven, en aan het rad op de groote as, dat het voornoemde rad beweegt 70 tanden, dan zou het toestel eenigszins nauwkeuriger met de ware beweging van Venus overeen zijn gekomen.  Immers de eerstgenoemde getallen, die wij gebezigd hebben, maken dat Venus na 20 jaar 3° 37' bij den waren stand ten achter is, terwijl de laatstgenoemde getallen in dezelfde 20 jaren Venus een klein weinigje te ver gevoerd zou hebben, maar slechts over een afstand van iets minder dan 15'.   Op ongeveer dezelfde wijze worden ook de aantallen gevonden van de tanden der radertjes die Mercurius in beweging brengen.  Immers als de periode der Aarde met betrekking tot de Ecliptica gesteld wordt op 365 dagen, 5 uren, 49' 15" 46"', en die van Mercurius op 87 dagen, 23 uren, 14' 24", of gemakshalve resp. op 365 dagen 5 uren 50' en 87 dagen 23 uren 15', dan wordt voor de verhouding der omwentelingen van Mercurius ten opzichte van die der Aarde gevonden 105190 : 25335, of 21038 : 5067, door de deeling van welke getallen, uitgevoerd op de hooger gezegde wijze, verkregen wordt 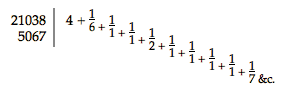en wanneer men de laatste breuk verwaarloost en de overige tot een gemeenschappelijken noemer herleidt zal ontstaan 847/204, welke getallen met de verhouding der bewegingen volgens welke deze Planeten bewogen worden zeer nauwkeurig overeenkomen.  Maar omdat 847 ontstaat uit de vermenigvuldiging der getallen 121 een 7, en 204 uit die der getallen 12 en 17 zijn op het jaarrad 1), dat zich bevindt op de gemeenschappelijke as, 121 tanden aangebracht, en is een hulp-asje aangebracht dat draaibaar is om twee vaste punten waarvan het eene zich bevindt op de as die door de Zon en het ringetje van Mercurius loopt,   1)  Zie tafel 3, fig. 4  [en tab. 2, fig. 3: D].

[ 406 ]

[ Lat. ]

en het andere is een zuiltje dat vast zit op de vaste Aardplaat.  Deze punten nu zijn zoover verwijderd van de banen van Mercurius en Venus, dat de tanden der raderen van Venus en de Aarde vrij onder het asje doorgaande daardoor in hun beweging niet gehinderd worden.  Dit asje nu heeft twee radertjes, één rondom elk uiteinde, waarvan het eene, welks tanden grijpen in die van het jaarrad, 12 tanden heeft, het andere echter hetwelk grijpt in den staanden cirkel die de Planeet draagt, 7 tanden heeft, terwijl die staande cirkel zelf 17 tanden heeft.  Hierdoor is het duidelijk dat tusschen de beweging der gemeenschappelijke as en die van het rad dat Mercurius draagt, de genoemde verhouding tot stand komt, n.l. die van 204 : 847.   Opdat het aantal tanden van de radertjes die de Maan rondvoeren gevonden worde, zal, als dezelfde jaarlijksche beweging wordt aangenomen van 365 dagen, 5 uren, 50' en een maanperiode van 29 dagen, 12 uren, 44' 3", of liever 45' voor het gemak der berekening, een verhouding 105190 : 8505 of 21038 : 1701 voor die der omwentelingen van Maan en Aarde gevonden worden; door deeling van welke getallen, evenals vroeger, ontstaat 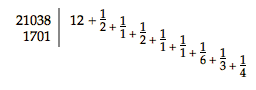  Indien echter als laatste breuk wordt aangenomen 1/6 en de voorafgaande breuken tot denzelfden noemer herleid worden, zullen ontstaan de getallen 1546 en 125, waarvan het eerste getal geen andere factoren heeft dan 2 en 773, maar omdat dit een te groot aantal tanden oplevert, zal het beter zijn in plaats van de breuk 1/6 de naast bijkomende 1/7 te nemen, waardoor ontstaan de getallen 1781 en 144, waarvan de eerste ontstaat uit 137 en 13, de tweede uit 12 en 12.  Hieruit zal men gemakkelijk komen tot de opgegeven [<] inrichting der tanden zoowel bij het grootere rad als ook bij de kleinere getande raderen.   Uit de wijze waarop het aantal gevonden is van de tanden die zoowel in de gemeenschappelijke as als ook in de raderen die de afzonderlijke planeten dragen, moeten worden ingesneden, is het duidelijk dat deze omwentelingen niet kunnen plaats hebben zonder dat na een zeker tijdsverloop een kleine fout optreedt in de verhouding welke wij aangenomen hebben dat de beweging der Aarde ten opzichte van de beweging

[ 407 ]

[ Lat. ]

van elke Planeet volgens de waarneming hebben moet; het is echter gemakkelijk te bepalen hoe groot deze kleine fout is.  Want opdat in het toestel de verhouding der ware beweging nauwkeurig zou worden waargenomen, zou het noodig zijn dat die verhouding der beweging precies overeen kwam met het aantal radertanden.  Bij het rad van Saturnus, opdat door dit voorbeeld de zaak duidelijk worde (welk rad op de gemeenschappelijke as zit) zijn er n.l. 7 tanden, maar bij het rad, dat Saturnus draagt 206 tanden.  Het is dus noodzakelijk dat Saturnus in een tijdsverloop van 206 jaren zijn omloop 7 maal volbrengt.  Maar daar de verhouding der beweging van de Aarde tot die van Saturnus is als 7708431 : 2640858, zal men vinden dat Saturnus in een tijdsverloop van 206 jaren zijn omloop niet precies zeven maal volbrengt, maar 7 1/1346 maal.  In elke 206 jaren komt dus Saturnus in zijn beweging in dit toestel 1/1346 van zijn cirkelvormige baan ten achter, en in elk jaar eenzelfde gedeelte van één tand, en in 1346 jaren zal zijn beweging één tand ten achter zijn; na dezen tijd moet men dus het rad van Saturnus één tand vooruit zetten.  Daar nu dit rad uit 206 tanden bestaat, die een volledigen cirkel van 360° uitmaken, zullen met elken tand 105' overeenkomen, met welke dus Saturnus vooruitgezet moet worden na een tijdsverloop van 1346 jaren, dus na 20 jaren 1' 34".  Dezelfde berekeningswijze is van toepassing bij de overige planeten.   Nu blijft ons nog over te verklaren, op welke wijze uit de omwenteling dezer raderen de vereischte ongelijkmatigheden der beweging volgen*).  Tot dit doel diene het volgende:

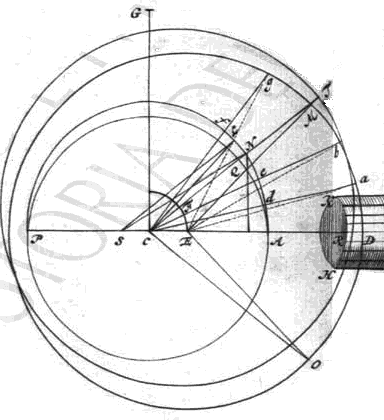
laat ANP een Planetenbaan zijn waarvan het middelpunt C is; zij S de Zon; en laat op SC het willekeurige punt E genomen worden, en laat ED zoo geconstrueerd worden dat CE : ED = de excentriciteit SC : den straal CA; laat dan met den straal ED en het middelpunt E de cirkel DM beschreven worden 1).  Men moet verder begrijpen dat aan den cirkel AL in zijn beweeglijk middelpunt C de cirkel DM onbewegelijk is vastgemaakt, welke laatste is ingesneden met onderling gelijke boven het vlak van den cirkel uitstekende tanden, welke cirkel dus noodzakelijk eveneens om het centrum C zal draaien.  Laat ons aannemen dat deze laatste cirkel in beweging gebracht wordt door de gelijkmatige draaiing van het rad KH, dat een naar het punt C gerichte as heeft, en welks tanden grijpen in die van het rad DM.  Zij zullen n.l. voldoende in elkander sluiten, hoewel wegens de excentriciteit van den cirkel de rij der tanden niet altijd een rechten hoek maakt met de as van het bewegende rad.  Ik beweer dat op deze wijze de Planeet in haar baan ongelijkmatig rondloopt en wel zoo dat hare beweging ten naastenbij overeenkomt met de hypothese van Kepler.   Immers 1) als men op den cirkel DM die uit het middelpunt E beschreven is een willekeurigen boog DO neemt, laat ons dan aannemen   [ *)  Zie ook OC XXI, p. 143-148.]   1)  Zie tafel 4, fig. 7.

[ 408 ]

[ Lat. ]

dat de tanden van dien boog door de draaiing van het rad HK de rechte lijn CD overschreden hebben, op dat oogenblik zal noodzakelijk de rechte lijn CO samenvallen met de rechte lijn CAD, hoewel niet zóó dat het punt O in D valt, maar meer naar binnen in R, daar CD, die gelijk is aan de som van CE en EO, grooter is dan CO.  Zoo groot als de hoek OCD is, zoo groot zal ook de hoek zijn, waarover de rechte lijn CAD bewogen zal zijn rondom het middelpunt C; dus zal, indien wij den hoek DCT gelijk maken aan den hoek DCO, CT de rechte lijn zijn, die CAD heeft bereikt, zoodat de Planeet van A tot het punt N is voortgegaan, waar de rechte lijn CT den cirkel AN snijdt die vanuit het middelpunt C is beschreven.

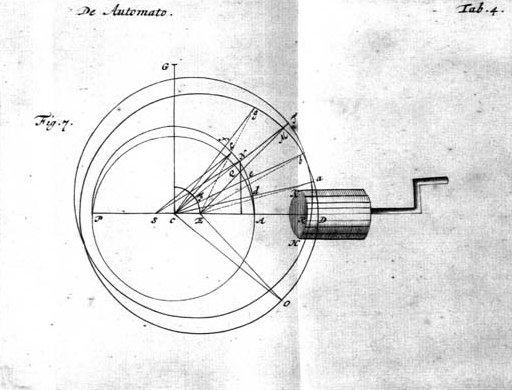
De cirkel DM echter zal, daar het middelpunt E is voortgegaan tot F, en FT gelijk aan ED moet worden genomen, den stand van den cirkel TR innemen.  Het blijkt nu uit die zelfde gelijkheid der hoeken OCD en DCT dat de boog DM, dien de rechte lijn CT van den cirkel ODM afsnijdt, gelijk is aan den boog DO.  Na verbinding van M met E, volgt daaruit, dat ook de hoek MED gelijk is aan DEO.  Indien dus een boog AL genomen wordt van evenveel graden als boog DM, en de lijn CL getrokken wordt, zal deze evenwijdig zijn met EM.  In de driehoeken CEM en SCL zullen dus de hoeken LCS en MEC gelijk zijn; ook zijn de zijden rondom die hoeken met elkander evenredig.  Volgens de constructie is n.l.   SC : CL = CE : EM,  omdat CL = CA en EM = ED.  Dus zullen ook de hoeken MCE en LSC gelijk zijn, en bijgevolg de zijden CM en SL evenwijdig.

[ 409 ]

[ Lat. ]

Dat derhalve door deze draaing der cirkels DM en AL de zich in A bevindende Planeet zóó langs den cirkel AL wordt bewogen, dat hare beweging ten naastenbij overeenkomt met de hypothese van Kepler, zal op de volgende wijze worden aangetoond.  Laat ondersteld worden dat de Planeet voortgegaan is van A tot N, dan zal het stuk NSA hare gemiddelde anomalie zijn; maar wegens de evenwijdigheid der lijnen SL en CN zal de driehoek NSC gelijk zijn aan den driehoek CLN, welke zeer weinig verschilt van den sector CLN.  Het stuk CLA en derhalve ook de boog AL zullen dus overeenkomen met de gemiddelde anomalie bij voortgang der Planeet van A naar N.  Indien we nu aannemen dat AQP de, volgens Kepler elliptische, baan is, dan zal de Planeet weliswaar in Q zijn (n.l. in het punt waar NQ, de loodlijn uit N op AP neergelaten, de ellips AQP snijdt) en niet in N; maar deze ellipsen verschillen zoo weinig van cirkels dat het verschil in ons toestel niet bemerkbaar is.  N zal dus de plaats zijn der Planeet, die zij bereikt tengevolge van de gemiddelde beweging AL, welke boog evenveel graden bevat als de boog DO of DM. 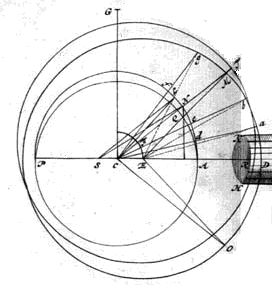Indien echter het bewegende rad op een willekeurige andere plaats gezet wordt b.v. in G, op gelijken afstand van het middelpunt C, waar de as van het rad op gericht is en indien het punt D dat op het rad ODM het verste van het middelpunt C verwijderd is onder het bewegende rad wordt geplaatst, en de Planeet opnieuw in A, haar Aphelium, dan blijkt het dat door een even groote draaiing van het bewegende rad in G als in D ook dezelfde hoeken rondom het middelpunt C worden afgelegd.  Waar ook het bewegende rad wordt geplaatst, de beweging der Planeet zal dus op dezelfde wijze ongelijkmatig worden, hoewel de tanden van het rad DM gelijk aangenomen zijn, alleen moeten de tanden van het bewegend rad K, waarvan de as gericht is naar het punt C, een zekere lengte hebben, waardoor het hun mogelijk wordt te grijpen in de tanden van den cirkel DM die telkens in andere punten de rechte lijn DC snijdt; en tegelijk moet er op gelet worden, dat, als de langste rechte lijn die van het middelpunt C naar den cirkel DM getrokken kan worden juist onder het bewegend rad K ligt, de Planeet geplaatst moet worden in het Aphelium van den cirkel ANL.  Omdat echter in ons toestel alle bewegende raderen op een en dezelfde as zijn geplaatst, zoo zal deze slechts ten opzichte van de middelpunten van 2 planeten den juisten stand kunnen hebben; daarom moeten wij verder overleggen hoe hetzelfde door ongelijkheid der tanden kan bereikt worden.  Laat ons daartoe onderstellen dat de cirkel DMP in gelijke deelen Da, ab, bM, Mg, gesneden is en dat naar elk daarvan uit het punt C rechte lijnen getrokken worden, n.l. Ca, Cb, CM, Cg, dan zullen deze de Planetenbaan ANL in ongelijke stukken Ad, de, eN, Nf, verdeelen.  Om deze reden zullen op den cirkel ANL even zoo vele ongelijke tanden gevonden worden als er gelijke tanden geplaatst zijn op den cirkel DM.  Indien dan nu het bewegend rad K op deze ongelijke tanden werkt

[ 410 ]

[ Lat. ]

(immers zij zullen voldoende aansluiting hebben, hoewel zij hier wat kleiner, daar wat grooter zijn) dan zullen met behulp van hetzelfde aantal tanden van het bewegend rad K, waardoor in het vorige geval de tanden van boog DM hun weg hebben afgelegd, nu de tanden van boog AN voorbijgaan, en zoo zal bereikt worden, dat tevens dezelfde ongelijkmatigheid der Planetenbeweging verkregen wordt, welke, naar wij hebben aangetoond, nagenoeg met de hypothese van Kepler overeenkomt. E I N D E

Noot 1 op blz. 389 en noot 1 op blz. 399 Volgens deze tabel (die met de teekening T, blz. 388-389 overeenkomt) zou men hebben: diameter ring Saturnus : diameter Zon = 1 : 3,4 De ware 1 : 5,4 ,, Saturnus : ,, ,, = 1 : 7,6 waarden 1 : 11,6 ,, Jupiter : ,, ,, = 1 : 5,5 zijn: 1 : 9,8 ,, Mars : ,, ,, = 1 : 166 1 : 202 ,, Aarde : ,, ,, = 1 : 110 1 : 109 ,, Venus : ,, ,, = 1 : 84 1 : 112 ,, Mercurius : ,, ,, = 1 : 308 1 : 295 De waarden die Huygens aanneemt wijken dus, vooral wat de planeten Saturnus en Jupiter betreft, sterk van de juiste waarden af. J. A. VOLLGRAFF

ERRATUM.  Op blz. 2 staat achter den naam van Dr. Vollgraff, astronoom te Voorburg; lees Middelburg.   [ Dit was in 1928. Heeft Johan Adriaan Vollgraff (1877-1965) eerder les gegeven in Zierikzee? Zie: "De eindexamenklas van 1906. Links dr. J.A. Vollgraff ..." (als leraar). Museum Boerhaave heeft een Vollgraff-collectie met o.a. een portret uit 1916.   Franse vertaling van Antide Janvier in Des révolutions des corps célestes par le mécanisme des rouages, 1812. Ook in:  Pierre Dubois, Histoire de l'horlogerie (1849), p. 162-177. Diens fig. 1-6 ook in L.Reverchon & P. Ditisheim, 'La machine planétaire et l'oeuvre astronomique de Huygens', L'Astronomie: revue mensuelle (Soc. Astr. Fr. 1930), p. 63.   Het planetarium van Huygens komt voor in de Catalogue of the special loan collection of scientific apparatus at the South Kensington Museum (London 1876/77), p. 427.]