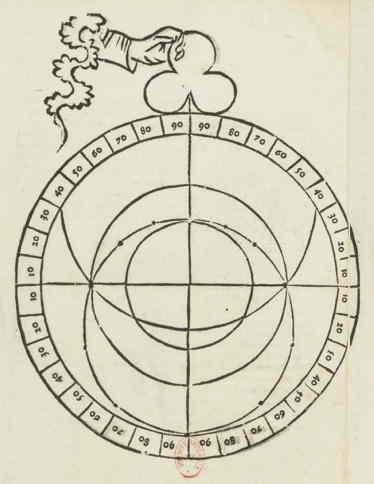
Figuur in ed. 1485 voorafgaand aan Liber de Nativitatibus.
[ Vgl. Chaucer (1387), fig. 17-19.]

[ a 2 ]

Begin van het boek van Abraham ibn Ezra over horoscopen.

Ook Abraham ibn Ezra heeft gezegd: het beste van de instrumenten om bij horoscopen de ascendant te vinden is het Astrolabium; en hoe volmaakter het is, des te beter. En na het astrolabium is het beste instrument het zogenaamde kwadrant*). Hierna de horizontale zonnewijzer. Hierna de vertikale zonnewijzer. Hierna de meting gedaan met water. ...   *)  Zie het 'Zutphens kwadrant' van rond 1300 (Stedelijk Museum Zutphen) en het 'Canterbury Astrolabe Quadrant' (British Museum).

[ ... ]

[ c 5v ]

vijftallen, was meer naar buiten geplaatst tussen de andere cirkels. Vervolgens heb ik vanaf het snijpunt van de dwarse diameter en de binnenste cirkel naar het onderste deel van de schijf 38 graden en 42 minuten geteld, en daar heb ik een teken gezet. Daarna spande ik een draad, vanaf het snijpunt van de andere diameter en de binnenste cirkel onder de ring, tot aan dat teken; en ik heb het snijpunt van die draad en de dwarse diameter aangetekend; en door dit snijpunt heb ik een cirkel getrokken om het middelpunt dat in het begin was bepaald; en deze cirkel heb ik gegraveerd voor de hemelequator. Dat getal nu van 38 graden en 42 minuten heb ik genomen omdat waar ik geboren ben de Ram [het Lentepunt] midden op de dag zo hoog komt. Als immers zo'n cirkel voor de hemelequator gesteld werd kon ik de gehele horizon binnen de rand van mijn instrument brengen. Toen ik dus de cirkel voor de hemelequator had getrokken op de manier zoals gezegd, heb ik aan beide kanten de ermee evenwijdige cirkels van Kreeft en Steenbok gegraveerd volgens de bijbehorende declinatie. Vervolgens heb ik de horizon beschreven voor een breedte van 51 graden en 12 minuten, dat is die van Mechelen, en deze paste geheel binnen de rand zoals ik gezegd heb. Daarna beschreef ik de cirkels evenwijdig aan de horizon, de almucantars, twee graden van elkaar. De horizon nu heb ik op de plaat goed verdiept, wegens de grotere bekendheid, en evenzo elke vijfde almucantar. Ik heb ook hoogtecirkels gegraveerd die men azimut-cirkels noemt, die de horizon en de ermee evenwijdige cirkels loodrecht snijden; de eerste daarvan, namelijk die welke door het ware oosten gaat, dat van de Ram, en door het zenith boven het hoofd en door het ware westen, heb ik diep in de schijf gemaakt, om hem meer te doen opvallen. Ook andere azimut-cirkels vanaf deze eerste naar het zuiden, oftewel naar de ring toe, liet ik snijden met de horizon en met de almucantars die in werkelijkheid ermee evenwijdig zijn, steeds per drie graden; maar vanaf die verdiepte cirkel meer naar binnen, in de richting van het middelpunt van de schijf dat als noordpool wordt gesteld, alleen per zes graden, wegens de beperkte ruimte. De kunst om dit alles te maken is in verschillende verhandelingen voldoende bekend gemaakt.*) Almucantars (Mashallah, ms 1276). Azimut-cirkels (Mashallah). Uurbogen onder de horizon (Mashalla). Vgl. ms 1432 en Reisch 1512. Evenzo heb ik twaalf uurbogen gegrift en wel boven de horizon, opdat we ze kunnen gebruiken wanneer we willen, en twaalf onder de horizon zoals de theorie van het maken leert; behalve dat er bij één enig verschil was, dat echter de manier om de uurbogen te trekken niet in de weg staat of verandert, noch de juistheid van de verdeling voor het vinden van de uren. Ik had namelijk binnen de cirkel van Kreeft, in de richting van het middelpunt van de schijf, een evenwijdige getrokken op een afstand van zes graden. En een andere buiten de cirkel van Steenbok, eveneens zes er vanaf. En over deze twee en over de helft van de hemelequator heb ik uurbogen aangelegd voorzover het dienstig was. En dit heb ik gedaan wegens enige dingen die later vermeld zullen worden. Maar omdat enige schrijvers van judiciële astrologie de vereffening van de aspecten, en van de herstellingen over de ongelijke uren en hun delen, zoals ook de vereffening van de huizen, duidelijk hebben gegrondvest, naar blijkt in hun werken. Daarom heb ik, opdat deze manier zich bij het instrument vanzelf zou aanbieden, deze verdeling bedacht:   *)  De figuren komen uit R.T. Gunther, Chaucer and Messahalla on the astrolabe (1929, manuscript.: 1276), bij p. 156-159. De verhandeling 'De compositione Astrolabii' van Mashalla (ca. 800) werd gedrukt in: Gregor Reisch, Margarita philosophica, 1512, fol. H1-M4v, met figuren. Uitleg van de stereografische projectie: J. D. North, 'The Astrolabe' in Scientific American, jan. 1974.   [ Ontcijferen van oude manuscripten kun je ook zelf proberen, zie 'Handschrift lezen'.]

[ c 6 ]

elk gedeelte namelijk van de drie al genoemde cirkels tussen uurbogen onder de horizon, heb ik in vijf gelijke delen gedeeld. En door elke drie punten van deze drie delen die op deze drie cirkels met elkaar overeenkomen, heb ik cirkelbogen getrokken op de manier zoals ze bij de uren ontstonden. Vervolgens heb ik de voet van de passer onbeweeglijk gezet op het middelpunt dat voor de pool gehouden wordt, en het andere been uitgestrekt; en ik heb veel cirkelbogen getrokken vanaf de bovenste van de uurbogen tot beneden, die ze dwars doorsneden op een afstand van zo goed als twee graden; en wel op de volgende manier. De twee eerste ruimtes van twee uren namelijk waren doorsneden met dwarse cirkelbogen, zoals ik heb gezegd; en ook met dezelfde indeling en maat de twee derde en de twee vijfde; maar de twee tweede, aan twee uren toegekend, en de twee vierde en de twee zesde ruimtes hadden onderling eenzelfde maat en indeling, die echter van de vorige verschilde in de maat, met zo goed als één graad, van samentrekking en uitzetting van de passer. Zodanig dat elke dwarsboog die twee uren verbond zo eindigde op een gemeenschappelijke uurboog, dat hij midden tussen twee dwarsbogen aan de andere kant het einde had op deze manier. En deze dwarsbogen zijn zeer handig voor een vlottere bewerking met aspecten en herstellingen, zoals bij gebruik zal blijken. En dit is de uiteenzetting van het graveren van mijn schijf op één van zijn zijden. En wegens een mening over huizen en aspecten die misschien niet geheel zonder reden is, hoewel deze door de schrijvers niet wordt uitgedrukt, heb ik de andere zijde van de schijf gegraveerd op de manier zoals ik zal zeggen. Ik heb namelijk op deze zijde eerst de rand beschreven, gelijk aan de eerste, en ik heb twee diameters getrokken, elkaar loodrecht snijdend in het middelpunt; en ik heb de rand bezet met graden en getallen zoals de eerste. Vervolgens heb ik binnen deze rand een hemelequator beschreven, geheel gelijk aan de eerste; en daarna heb ik de horizon gegraveerd volgens de breedte van Mechelen, op de manier zoals ik gezegd heb. En door het zenith van deze horizon en door het ware Oosten en Westen heb ik een hoogtecirkel beschreven die ik, omdat hij wegens zijn grootte niet helemaal binnen de koperen schijf bevat kon worden, voor het overige liet doorlopen op een houten schijf, aansluitend op de koperen schijf*). En door deze hoogtecirkel op een daarvoor geschikte manier per twee graden te verdelen — op de manier waarop elke grote cirkel op de planisfeer kunstvaardig te verdelen is, zoals ik hierna zal uiteenzetten over de Dierenriem — heb ik grote cirkels getrokken door elke twee punten van de verdelingen van deze hoogtecirkel tegenover elkaar en over beide gedeelten van de horizon en de diameter die omlaag gaat vanaf de ring en die de plaats van de meridiaancirkel inneemt. En op deze manier heb ik de graveringen op deze zijde van mijn schijf voltooid.   Vervolgens heb ik een andere schijf genomen, goed vlak gemaakt en behoorlijk sterk, voldoende om kromming te weerstaan; en ik heb die eerst cirkelvormig afgesneden, zodat hij   *)  Vergelijk de figuur in Johannes Stöffler, Elucidatio, 1513, fol. 6v.

[ c 6v ]

precies binnen de rand van de andere schijf kon worden bevat, behalve een uitsteeksel dat ik heb bestemd voor een tandje of almuri*). Daarna heb ik de voet van de passer op het middelpunt van de schijf geplaatst en met zijn beweeglijke voet heb ik een cirkel beschreven voor de hemelequator, gelijk aan die op de andere schijf, en die heb ik per graad verdeeld. Vervolgens heb ik de Dierenriem vorm gegeven, volgens de bijbehorende declinatie zoals de theorie leert; deze heb ik zodanig ingericht dat er naast die cirkel die als ecliptica gesteld wordt andere daarmee concentrische cirkels waren, zodat er graden met hun getallen konden worden gegrift. Ook heb ik één cirkel beschreven voor de lijn die gesteld wordt op zes graden van de ecliptica-lijn, naar het middelpunt van de schijf toe; en een andere buiten de ecliptica op evenveel graden; volgens de theorie waarmee op hun manier de lijnen evenwijdig met de horizon beschreven worden, die almucantars worden genoemd. Verder heb ik aan de binnenste van deze concentrische cirkels nog een cirkel toegevoegd, concentrisch ermee, naar de ecliptica toe, zodat de verdelingen in graden daar konden worden aangegeven. En ann de buitenste heb ik er meer toegevoegd en grotere, voor de verdelingen in graden, en zodat het aantal ervan en ook de namen van de Tekens daar passend bij konden worden geplaatst. Vervolgens, nadat de ecliptica-pool op de schijf was gegrift, volgens wat wordt vereist°), heb ik een grote cirkel getrokken door deze pool en door beide gemeenschappelijke snijpunten van hemelequator en ecliptica, en om dit gedaan te krijgen had ik een andere schijf erbij nodig en door het middelpunt van deze grote cirkel heb ik een rechte lijn getrokken evenwijdig aan de diameter die door de al genoemde snijpunten gaat, doorlopend en gericht; en voor dit doortrekken zijn toegevoegde houten schijven nodig, wegens de grote lengte van deze lijn#). Daarna heb ik de schijfdiameter die vanaf de almuri omlaag gaat en die de andere die door de genoemde snijpunten loopt loodrecht snijdt, doorgetrokken totdat hij deze grote cirkel in twee gelijke delen verdeelde. Vervolgens heb ik één van hun helften, of beide omdat het niet uitmaakt bij deze grote cirkel, in negentig graden verdeeld. En ik heb een draad gespannen vanaf de ecliptica-pool naar een van deze verdelingen en ik heb tekens gezet op die lange evenwijdige lijn die ook deze grote cirkel in twee gelijke delen verdeelt, namelijk op de plaatsen waarover de genoemde draad loopt, als hij wordt gespannen zoals gezegd. Dat wil zeggen door de draad vanaf de ecliptica-pool steeds zo te spannen, dat hij de genoemde verdelingen zou raken, en ook die lange evenwijdige lijn. En toen zette ik de voet van de passer onbeweeglijk op een van deze tekens die op deze lijn zo waren aangegegeven, en ik zette de beweeglijke voet uit tot op de ecliptica-pool; en met deze opstelling toegepast op alle aangegeven tekens heb ik met de beweeglijke voet van de passer stap voor stap de hele ecliptica verdeeld en ook de lijnen op gelijke afstanden ervan, aan beide kanten op zes graden. En dit is de algemene manier om grote cirkels, en lijnen op gelijke afstanden ervan, te verdelen in graden of andere gedeelten, ik bedoel met een verdeling die met cirkels wordt gemaakt; zo kan immers de ene met de andere verdeeld worden als er één door de polen van de andere gaat. Het is hier niet de plaats om een bewijs hiervan te geven. Er is ook een andere verdeling van de ecliptica en van alle grote cirkels op een planisfeer, die gebeurt met rechte lijnen; en   *)  Almuri: uitsteeksel bij Steenbok, zie figuur. Chaucer (in Gunther 1929, p. 25), "Thy almury is called the denticle of Capricorn or else the calculator."   °)  Zie de figuur in Stöffler 1513, fol. 15v.   #)  Fig. Stöffler 1513, fol. 16v.

[ c 7 ]

deze heb ik eveneens gebruikt: ik plaatste namelijk een rechte liniaal of een draad op de pool van de ecliptica en op een van de verdelingen van de hemelequator, die verdeeld was per graad; en waar de liniaal of de draad de ecliptica raakte, daar zette ik een merk; en op deze manier heb ik de hele ecliptica-lijn in graden verdeeld. Op dezelfde manier kunnen andere grote cirkels met rechte lijnen worden verdeeld in hun delen, door namelijk een draad te plaatsen op een pool van de te verdelen cirkel en die te spannen over zoveel gedeelten van de hemelequator als we willen hebben, tot op de te verdelen cirkel; en waar hij tegen de te verdelen cirkel komt moeten we er een teken op aanbrengen; en zo wordt de verdeling tot aan het eind voltooid. Maar om niet iets dat met de verdeling van de cirkels te maken heeft over te slaan, zal ik nog een kleinigheid over de verdeling van de ecliptica toevoegen. Ik bedoel dat beide polen ervan als volgt te verkrijgen zijn: we gaan dan op de cirkel van de hemelequator vanaf een van de twee snijpunten van ecliptica en hemelequator, in de richting van de zuidelijke delen van de ecliptica, tellen volgens de grootte van de helling van de ecliptica, en waar onze telling stopt maken we een teken; daarna spannen we een draad vanaf het snijpunt er tegenover tot aan het gemaakte teken en waar de draad de diameter van de schijf snijdt, zetten we een punt, omdat daar de ene pool is. Vervolgens gaan we vanaf dat zelfde snijpunt van hemelequator en ecliptica, waar­vandaan de draad al gespannen was, dezelfde helling als eerst aftellen, maar naar de andere kant; en door de plaats waar het aftellen stopt spannen we de draad vanaf het snijpunt waar­vandaan hij eerst gespannen was; tot waar hij de recht doorgetrokken diameter van de schijf snijdt, en op de plaats van dit snijpunt zetten we een punt, omdat daar de tweede pool is. Vervolgens verdelen we het gedeelte van de diameter tussen die beide polen in twee gelijke delen; dan zetten we de voet van de passer in het midden, en we zetten de omtrek uit tot aan de beide polen en de beide snijpunten van ecliptica en hemelequator; en we draaien de passer rond, en op deze manier maken we een hele cirkel; en het is wel noodzakelijk dat deze cirkel door die vier punten gaat als de voorgaande vormen juist zijn getrokken, en door het middelpunt van deze grote cirkel moet een lange lijn worden getrokken, evenwijdig aan de diameter die door de gemeenschappelijke snijpunten van ecliptica en hemelequator gaat. Hierna moet één kwart van deze cirkel verdeeld worden in 90 gelijke delen; en er moet een draad gelegd worden op de pool van de ecliptica-cirkel die het tegenoverliggende kwart begrenst, en bij het spannen ervan naar alle afzonderlijke deelstreepjes van het in graden verdeelde kwart, moeten merktekens gezet worden waar die draad de diameter van deze cirkel snijdt. En door deze merktekens en door beide polen van de ecliptica moet de passer geleid worden waarmee de ecliptica moet worden verdeeld. Maar om de middelpunten te vinden van al deze grote cirkels waarmee de ecliptica te verdelen is, moet er een verdeling zijn van de helft van die grote cirkel, die eerst tot 90 delen werd verdeeld, ik bedoel de helft ervan die loopt van de ene ecliptica-pool naar de andere, en zoals daarmee moeten er tekens gemaakt worden op die lange evenwijdige lijn. En die tekens zijn met de hierboven verhaalde manier de middelpunten geworden van alle grote cirkels. En op een dergelijke manier kan

[ c 7v ]

elke cirkel op een planisfeer worden verdeeld, behalve de hemelequator en daarmee evenwijdige cirkels; en eveneens met deze theorie heb ik op mijn schijf de verdeling van de ecliptica onderzocht. En daarna heb ik de vaste sterren op deze schijf geplaatst, met grote cirkels die door de polen van de ecliptica gaan en door de graden van de ecliptica die bij de sterren horen in de lengte; en met lijnen evenwijdig aan de ecliptica, op de manier waarop de evenwijdigen worden afgebeeld, volgens de breedten van de sterren. Dat is te zeggen, ik heb sterren uitgekozen die het meest in het oog lopen en die het meest nodig zijn in de judiciële astrologie. En van elk van de achtenveertig sterrenbeelden die er gezet konden worden heb ik minstens één ster en soms meer sterren gezet. Vervolgens heb ik alle overtollige delen uit deze schijf weggehaald en het volvellum*) afgemaakt, heel nauwkeurig onderzocht; waarop inderdaad elke ster die in mijn land kan verschijnen passend kon worden geplaatst. Nu was de Dierenriem op dit volvellum zo goed als verdubbeld, zodanig dat de ene een brede cirkel was met op het eind van de ene rand beschreven de ecliptica-lijn met zijn verdelingen en getallen, en op het eind van de andere rand van dezelfde brede cirkel was een andere cirkel met zijn verdelingen, zes graden van de ecliptica af. Die brede cirkel die de ene Dierenriem was had namelijk zo'n breedte, dat hij precies zes graden vanaf de ecliptica bevatte aan de binnenkant. En de andere Dierenriem was eveneens zes graden van de ecliptica verwijderd, aan de buitenkant, en deze Dierenriem was zo wijd, dat de verdelingen in graden en hun aantal, met vijf toenemend, en ook de namen van de Tekens er passend ingeplaatst konden worden, zoals ik eerder heb verhaald. En de ruimte binnen de twee Dierenriemen heb ik leeg gemaakt, behalve enige kleine delen die niet toelieten dat beide Dierenriemen van stand zouden veranderen, en eveneens behalve enige kleine puntige uitsteeksels bestemd voor enkele sterren. En dit is de manier waarop ik mijn instrument bewerkt heb. Tenslotte heb ik dan het volvellum en de schijf met een geschikte pin aan elkaar bevestigd, en zo heb ik mijn hele astrolabium voltooid. Maar de achterkant van het astrolabium heb ik niet behandeld, omdat een groot kwadrant meer kan en het gebruik ervan betrouwbaarder is.

[Over het gebruik van het astrolabium].

En nadat we uitleg hebben gegeven over de bouw van ons astrolabium lijkt het me geschikt er iets bij te voegen over het gebruik en het profijt ervan. Met weglating van veelsoortige en veelzijdige passages, verspreid over verschillende verhandelingen, zal ik dan voorzover ik het kan vrij goed weergeven en uiteenzetten dat weinige, dat mij nog leek te moeten worden toegevoegd. Maar eerst moet één ding goed worden begrepen waarvan de bespreking geenszins te veronachtzamen is; en dat is dat het bij het opnemen van de uren gebeurt dat we ons soms vergissen, als we niet opnieuw denken aan de verscheidenheid van dagen en uren waarnaar de loop van de planeten wordt vereffend en van de uren die met instrumenten worden opgenomen; terwijl juist wordt voorgeschreven dat de ascendant en de overige huizen en ook de aspecten van de planeten daarnaar worden vereffend. Er is daaronder immers een verschil, soms groter, soms kleiner en soms geen; zoals wordt uitgesproken   *)  De opengewerkte draaischijf; andere namen: 'rete' (net), 'spin', 'araignée' (zie bij Astrolabium en schema); 'volvellum' komt voor in Metius 1627, als "omdrayende ronde schyve".

[ c 8 ]

door Ptolemaeus en Geber en andere meesters van de waarneming*). Toch leert Albategni ons vrij duidelijk hoe voorzichtig we moeten zijn in het ons behelpen met dit verschil, zoals blijkt in het vierendertigste hoofdstukje van zijn boek°). Laat ik nu hier ook kort zeggen hoe we te werk moeten gaan. Wanneer een tijdstip bekend is dat met een of ander instrument is waargenomen, waarbij we de ware plaatsen van de planeten willen vinden, en als het om ongelijke uren gaat, dan moet het herleid worden tot gelijke uren, zoals elders gezegd zal worden; als een tijdstip op een dergelijke manier bekend is, zeg ik, zullen we de tijdsvereffening nemen in tabellen van opkomst van de rechte cirkel die opgesteld wordt in de richting van de graad waarin de Zon op dat tijdstip staat en dit met bijtelling van de beweging van de achtste sfeer#); en die tijdsvereffening herleid tot de tijd in uren, zoals bekend, zullen we van het bekende tijdstip aftrekken. En met wat overblijft zullen we de plaatsen van de planeten opsporen. En deze zo onderzochte uren heten vereffeningsuren; maar de uren die met een instrument worden opgenomen, voorzover ze tenminste tot gelijke uren gemaakt zijn, worden genoemd uren van de streek; en op deze uren worden de ascendant en de overige huizen vereffend. Als daarentegen de plaats van een planeet bekend is, zoals de plaats van een conjunctie van enige planeten of van een oppositie ervan, of de ingang van een bepaalde planeet in een bepaalde graad van een bepaald Teken, en als we het tijdstip willen vinden waarop dit gebeurde of gebeurd was, dan moeten we de tijdsvereffening volgens de vermelde manier toevoegen aan de tijdstippen die volgen uit de komst van een hemellichaam op een plaats; zoals we eerder, toen het tijdstip bekend was en we de plaats van het hemellichaam wilden vinden, de tijdsvereffening hebben afgetrokken van die tijdstippen. En zo moeten de uren onderzocht worden om te weten welke daarvan vereffeningsuren zijn en welke uren van de streek. De oorzaak nu van dit verschil tussen deze twee soorten uren wordt voldoende verklaard door Ptolemaeus, Geber, Albategni, Abraham en andere meesters van de waarneming; daarom leek het me overbodig deze hier uiteen te zetten.   Hoe de plaatsen van planeten met ons astrolabium worden gevonden volgens een schatting die dichtbij de waarheid ligt; zowel in lengte als in breedte. Als we echter de plaats van een planeet met dit astrolabium willen opsporen, zoals hij aan ons verschijnt, zullen we zijn verheffing boven de horizon opnemen met een kwadrant of gelijkwaardig instrument; ook zullen we hiermee waarnemen in de richting van welk gedeelte van de horizon deze verheffing is; en dit wordt door sommigen genoemd het zenith van het hemellichaam. En dat is niet alleen van toepassing op dit voorbeeld, maar ook op vele andere; vooral wanneer het hemellichaam waarmee we ons willen bezighouden dichtbij de meridiaan staat, omdat dan dezelfde verheffing lang duurt. Zodat als we met alleen de verheffing tevreden zijn het kan gebeuren, dat we ons soms zeer vergissen bij het aannemen van de uren en graden van de ascendant en van de huizen en andere. Daarom lijkt het me noodzakelijk een instrument te hebben waarmee tegelijk kunnen worden waargenomen de verheffing van het hemellichaam en ook zijn zenith, oftewel hoe ver het van de meridiaan verwijderd is aan de ene kant of de andere, of van de hoogtecirkel die   *)  Magistri probationum, magistri considerationum: "astronomers who based their tables and calculations on observation" (Steel 2018, p. 45).   °)  Albategni, De motu stellarum, Nor. 1537, fol. 45v.  Idem, De scientia stellarum, Bon. 1645, p. 114.   #)  De beweging van de sterrenhemel die het Lentepunt doet verschuiven.

[ c 8v ]

door het ware oosten en westen gaat. En misschien door het plaatsen van een groot kwadrant op een vlak stuk marmer of op een grote bronzen tafel, op een daarvoor geschikte en handige manier, kunnen deze beide gemakkelijk tegelijk worden gevonden, te weten de verheffing van een hemellichaam en het zenith ervan.   Als dan de verheffing van een bepaalde planeet is opgenomen en ook zijn afstand van de meridiaan, vooral wanneer hij dichtbij die meridiaan staat, moet van deze twee het overeenkomstige worden opgezocht in almucantar en azimuth van onze schijf, en daar moet een merkteken gezet worden. Vervolgens, als het tijdstip van waarneming is vastgelegd, zal ik het volvellum de stand geven die het waarnemings­tijdstip vereist; en dan zal ik het merkteken bekijken dat eerder is gemaakt en nagaan in de richting van welk Teken en welke graad het terecht­gekomen is, omdat in die graad dan de planeet zal zijn en dit met de beweging van de achtste sfeer. En daarmee zal ook de breedte van de planeet verkregen worden, en of deze noordelijk is of zuidelijk. Ook zal de grootte van de breedte door evenredige schatting nauwkeurig genoeg verkregen worden zolang de breedte van de planeet niet groter is dan zes graden; want als deze groter zou zijn, zou het moeilijk zijn met ons instrument de grootte ervan nauwkeurig te onderzoeken. Ik heb namelijk de breedte van de Dierenriem liever tot slechts zes graden aan beide kanten willen uitstrekken, om de delen van de breedte sneller en makkelijker te vinden, want bij minder is beter te zoeken; en verder omdat de breedten van de drie buiten­planeten, waarvan in de judiciële astrologie de invloed groter gemaakt moet worden, daarbinnen blijven; en als enige breedten van binnen­planeten groter zouden kunnen zijn, zouden ze toch ook met ons instrument te vinden zijn voorzover dit van belang is voor de beoordelingen, en dit is omdat we ermee kunnen vinden welke van de planeten boven een andere werd verheven. Ook de heen- en terug­gaande bewegingen en stilstanden van de planeten*) kunnen we met dit instrument onderzoeken. Als immers een geschikte tussentijd wordt aangehouden tussen twee waarnemingen, zullen hun plaatsen aangeduid worden op de manier zoals ik al heb verhaald over het vinden van de plaats van een planeet; en hiermee zal duidelijk blijken of bij de twee waarnemingen dezelfde graad aan de ecliptica behoort, omdat de planeet dan stationair is; of dat met de tweede waarneming overeenkomt een graad die voorafgaat aan de graad van de eerste waarneming, omdat het dan een teruggaande beweging is; en bij een volgende is het een heengaande beweging.

Over het vinden van de aspecten van planeten volgens de opvatting van Ptolemaeus en Albumazar en zoveel anderen.

Bij degenen die in de kunst van de Astrologie meer deskundig zijn is er unanieme overeenstemming, dat een planeet die in het begin van een huis staat, zich ten opzichte van het begin van het in de rij der huizen volgende derde huis, en ten opzichte van het begin van het voorgaande elfde huis, in het zeshoeks-aspect bevindt. Ook dat hij stralen van het driehoeks-aspect werpt op het begin van het vijfde huis dat er op volgt, en op het begin van het negende huis ervoor; er zijn ook   *)  Zie: 'Apparent retrograde motion'.

[  d  ]

projecties van stralen van het vierkants-aspect van dezelfde planeet op het begin van het voorgaande tiende huis en van het volgende vierde. Daarom, als de huizen zijn vereffend volgens de breedte op aarde, zoals in het betreffende hoofdstukje staat, zullen daarmee de projecties van stralen van een aspect van een planeet als vaststaand worden beschouwd, volgens de manier zoals gezegd is. Als nu een hemellichaam in het begin van geen enkel huis staat, maar erbinnen, weet je dat het volgens een bepaalde verhouding stralen van een aspect werpt op de graad van dat huis waarbij dat aspect past, volgens de genoemde opstelling; ik bedoel de graad die in een zodanige verhouding staat tot dat hele huis waarvan het een graad is, als de graad van het hemellichaam zich verhoudt tot zijn huis; en wel het huis nemend met betrekking tot de graden van de klimmingen, naar gelang het samengestelde delen van uren bevat. Maar opdat het bedenksel van deze verhouding voor ons gemakkelijk en handig is, moet met ons instrument, dat hiervoor en voor andere dingen is verzonnen, op de volgende manier worden gewerkt. Als het hemellichaam waarvan het aspect wordt gezocht, en het huis waarnaar het aspect ervan wordt gericht, tussen de graad van de ascendant en de hoek van de aarde zijn, moet het begin van het huis waarin het hemellichaam is, worden geplaatst op de lijn van de hoek van de aarde; en bekeken moet worden waar dan de graad van de ascendant is. Daarna moet het volvellum zó bewogen worden, dat de graad van het hemellichaam op de hoek van de aarde valt; en bezien moet worden tot waar de graad van de ascendant is gekomen, en heel zorgvuldig moet worden aangeduid de hoekafstand ervan tot de eerste plaats van beschouwing; en dit met de op het instrument gemaakte verdelingen en met delen van die verdelingen. Vervolgens moet het begin van het huis waarnaar het aspect wordt gericht op de lijn van de hoek van de aarde geplaatst worden, en weer moet de plaats van de ascendant aangeduid worden. Daarna moet het volvellum zó bewogen worden, dat de afstand van de graad van de ascendant tot de nu aangeduide plaats even groot is, als de hoekafstand ervan tot de plaats van beschouwing bij de eerste opname van de afstand; en de graad die nu de lijn van de hoek van de aarde raakt zal de graad zijn waarin het aspect valt.   Als echter beide, namelijk het hemellichaam en het huis dat het aanziet, tussen de pool van de aarde en de westelijke graad zijn, moet het begin van het huis waarin het hemellichaam is, geplaatst worden op de lijn van de hoek van de aarde, zoals eerst, en aangetekend moet worden de boog waarop het nadir*) van de graad van de ascendent valt. En voor dit aantekenen is van groot belang het ongelijk eindigen van de dwarsbogen op sommige uurbogen. Daarna moet het volvellum bewogen worden tot waar de graad van het hemellichaam de lijn van de hoek van de aarde raakt; en aangeduid moet worden de verwijdering van het nadir van de graad van de ascendant vanaf de aangetekende boog. Vervolgens plaatsen we het begin van het huis waarnaar de stralen gericht worden, op de hoek van de aarde. En de bewerking gaat geheel op dezelfde manier in dit kwadrant met het nadir van de ascendant, als ik eerder heb gezegd over de ascendant zelf. En zo wordt de graad van het aspect gevonden met het vallen ervan op de hoek van de aarde.   Als nu het hemellichaam in het eerste kwadrant staat en het huis waarnaar het aspect gaat in het tweede, moet het begin van het huis van het hemellichaam geplaatst worden op de hoek van de aarde. En met de beweging van het volvellum wordt aangeduid het aantal verdelingen en delen ervan over de afstand tot de graad van de ascendant, zoals wat we hebben voorgeschreven in het begin heel zorgvuldig aan te duiden. Ons biedt zich vervolgens aan dat het begin van het huis waarheen de stralen worden gezonden op de hoek van de aarde wordt geplaatst   *)  Nadir: tegenpunt; zie Gunther 1929, p. 186 (Mashallah): "nadir of the ascendant degree".

[ dv ]

en, als de boogpositie van het nadir van de ascendant-graad zorgvuldig is aangetekend, dat deze van dezelfde boog wordt verwijderd met nabootsing van de afstand tussen de twee plaatsen die in het eerste kwadrant zijn aangetekend, dat wil zeggen: volgens zo'n aantal verdeligen en delen ervan wordt het nadir verwijderd van de al aangetekende boog, in oostelijke richting, als het aantal verdelingen en delen ervan was, bevat in de afstand van de twee plaatsen die in het eerste kwadrant zijn aangetekend. En de graad die dan op de hoek van de aarde is gevallen, zal de graad van het aspect van het hemellichaam zijn.   Maar als het hemellichaam in het tweede kwadrant verblijft, en het huis dat het aanziet in het eerste, moet de nu gestelde bewerking worden omgekeerd. Ik zal namelijk de eerste afstand vinden met het nadir in het tweede kwadrant; vervolgens zal ik een daaraan gelijke nemen met de graad van de ascendant in het eerste; en de graad waarop de stralen terechtkomen zal steeds vallen op de lijn van de hoek van de aarde.   Nu moet begrepen worden dat, als graden van aspecten worden gevonden op een boog die onder de horizon is, met diezelfde gevonden kunnen worden de graden van aspecten boven de horizon. Immers, een graad van een driehoeks-aspect aan de ene kant ligt tegenover een graad van een zeshoeks-aspect aan de andere kant. En een nadir-graad van een zeshoeks-aspect hier, is zelf een graad van een driehoeks-aspect daar; en een graad van een vierkants-aspect rechts staat tegenover een graad van een vierkants-aspect links. Omdat evenzo geldt: als de graad van het hemellichaam waarvan het aspect gezocht wordt, boven de horizon blijft, moet gewerkt worden met het nadir van dezelfde graad in plaats van die graad van het hemellichaam; en ook met het nadir van het begin van het huis waarnaar de stralen zich richten, als dat huis boven de aarde blijft. Projecties van stralen in tegengestelde kwadranten zijn immers gelijk.   Verder: als het hemellichaam waarvan we het aspect zoeken een breedte heeft, geven we het de plaats op ons instrument en daarna moet de instructie gevolgd worden die ik hierboven heb gegeven. Ook het werk van herstellingen*) kunnen we met hetzelfde instrument vrij vlot uitvoeren. Ik plaats namelijk het volvellum in overeenkomst met de hemel op het tijdstip waarop ik wil herstellen; en ik beschouw eerst of de plaats van de significator, oftewel de graad die ik wil herstellen, onder horizon is of erboven. Omdat ik, als deze er onder is, die plaats of graad neem, en een lijn of boog aanteken op de onderste schijf waarboven die plaats of graad staat bij die stand; ik teken ook de plaats van de almuri aan op de rand. Daarna beweeg ik het volvellum zoals het behoort totdat de plaats waar de herstelling eindigt, op die aangetekende boog of lijn valt; en de plaats van de almuri teken ik weer op de rand. En de graden, bevat tussen de twee op de rand getekende plaatsen, zullen de graden van herstelling zijn. Als echter de plaats van de significator, of de graad die hersteld moet worden, niet op een boog valt en ook niet op een lijn, maar in de ruimte, beschouw ik de verhouding van de graad of de plaats van de significator ten opzichte van de dichtstbij­zijnde boog of lijn — en hiervoor zijn nuttig die dwarsbogen die de uurbogen snijden — en ik teken de plaats van de almuri op de rand, zoals eerder. Vervolgens zet ik de graad waarop de herstelling eindigt op dezelfde verhouding tot die boog of lijn; en weer teken ik de plaats van de almuri aan   *)  Lat.: directionum. Zie Adriaan Metius, Fundamentale onderwijsinghe ... (1627) 2.3, p. 83: 'Van de Directie ofte herstellinghe'. Op p. 84: "hoe veel graden van de Aequinoctiael met de Globe worden omgedreven ende verloopen / terwylen de directie (het zy directa ofte conversa) volbracht wordt / want in veel [zoveel] jaren tijdts / als daer gevonden worden graden verloopen te zijn / sal de beduydinge ofte gheschiedenisse van den promissor ofte significator volbracht worden." Carlo Antonio Manzini, Tabulae primi mobilis (1626), begin: "Directio, seu deductio".

  d 2

op de rand. En de graden tussen de twee op de rand aangetekende plaatsen gevat, zullen de graden van herleiding zijn. Als nu de plaats van de significator, of de graad die hersteld moet worden, boven de horizon is; evenzo ook de eindplaats van de herstelling die met deze significator overeenkomt, of die nu boven de horizon is of eronder, in elk van deze gevallen moet worden gebruik gemaakt van de tegenover­liggende graden; en dan is de bewerking volgens de al gegeven instructie. Maar als de plaats van een significator die onder de horizon ligt, een breedte heeft, moet aangeduid worden een boog of lijn of ruimte die met deze breedte overeenkomt; en verder is de procedure zoals ik gezegd heb. En als de plaats van een significator die boven de horizon ligt, een breedte heeft, moet de tegengestelde graad worden genomen bij de tegengestelde breedte; en er moet gehandeld worden zoals eerst.   Verder is de kennis van ascendanten der Tekens onder de hemelkwadranten dezelfde als de kennis van herstellingen, want als de ene bekend is, is de andere ook bekend; laat het dan voldoende zijn dat de ene voor beide is genomen. Het moet ons verder niet onbekend zijn, dat bij het onderzoek van de vereffening van startpunten van huizen, en van aspecten van dwaalsterren, het bij nauwkeurig zoeken altijd noodzakelijk is, de plaatsen van de planeten met toevoeging van de beweging van de achtste sfeer te vereffenen; opdat we, als de plaats van de Zon met deze toevoeging is afgewogen, de uren precies kunnen verkrijgen, en de startpunten van de twaalf huizen, en zo uiteindelijk de graden van aspecten. En na het vinden van dit alles moet dezelfde vereffening van de achtste sfeer worden afgetrokken van zowel alle startpunten van huizen, als van alle plaatsen van planeten waarbij ze was opgeteld, zoals ook van de graden van aspecten die met de voorgaande instructie zijn gevonden. En zo zal al het genoemde met alle nauwkeurigheid overblijven, volmaakt afgewogen. Op dezelfde manier moet het gedaan worden bij de herstellingen. Het is immers duidelijk voor wie het beschouwt, dat wanneer uren en ascendanten van tekens, en andere dingen die hiermee worden gevonden, genomen zijn ten opzichte van de Dierenriem van de negende sfeer, en wanneer we beoordelingen ten opzichte van de Dierenriem van de achtste sfeer en dit zojuist genoemde werk achterwege laten, we in een lelijke fout vervallen. Als tenminste de oordelen in de astrologie zijn gegeven volgens de ligging van de plaatsen van hemellichamen ten opzichte van de negende sfeer; en de betrouwbaarheid van deskundigen zou dit kenbaar maken. Veel meer voel ik ervoor dat de plaatsen van de planeten met hun aspecten en twaalf huizen, en andere dingen, met toevoeging van de beweging van de achtste sfeer vastgesteld blijven, zonder enige later bijkomende aftrekking ervan.

Over aspecten met een andere manier.

Als iemand echter huizen en aspecten en andere dingen wil vereffenen met die manier, waarbij we ons voorstellen dat het halfrond in gelijke delen wordt verdeeld door grote cirkels, die gaan door beide snijpunten van de meridiaan-cirkel en de horizon, de hoogtecirkel die gaat door oost en west gelijkelijk verdelend — omdat deze manier sommigen misschien logisch zou toeschijnen — dan moet het volvellum aangebracht worden op de zijde van de schijf die overeenkomt met deze voorstelling, en zodanig opgesteld dat de graad van de ascendant

[ d 2v ]

op dat tijdstip, waarop we de huizen en aspecten willen vereffenen, valt op het oostelijk deel van de horizon. En omdat die grote cirkels die door de genoemde snijpunten gaan telkens twee graden van elkaar afstaan, tellen we vanaf het oostelijk deel van de horizon in de richting van de hoek van de aarde vijftien bogen van die grote cirkels af; omdat deze behoren bij het eerste huis. En waar de zestiende boog de ecliptica snijdt, zonder beweging van het volvellum uit de gestelde opstelling, daar zal het begin van het tweede huis zijn. Op gelijke manier moet gedaan worden met het derde en vierde en alle andere. En dit is de manier om huizen te vereffenen langs deze weg.   Ook een aspect is volgens deze manier gemakkelijk te vinden. Beschouwd moet worden de graad van de ecliptica waarop de planeet staat, waarvan we het aspect zoeken, en aangeduid moet worden de cirkel op de schijf eronder die onder deze graad doorgaat; en als de planeet een breedte heeft moet het zijn volgens wat erbij behoort. En steeds moet aangeduid worden de cirkel die daaronder loopt; en vanaf deze aangeduide cirkel tellen we naar beide kanten dertig van die cirkels; en waar de eenendertigste de ecliptica treft, daar zal het zeshoeks-aspect van die planeet zijn, het ene rechts, het andere links. Evenzo tellen we vanaf dezelfde aangeduide cirkel vijfenveertig van die cirkels, en waar de zesenveertigste de ecliptica raakt, daar is het vierkants-aspect. Evenzo doen we met het driehoeks-aspect op zijn manier. Of we kunnen van elk van beide zeshoeks-aspecten het nadir nemen, omdat het in beide gevallen hetzelfde is; aangezien immers al die cirkels grote cirkels zijn, zullen ze noodzakelijkerwijze steeds gaan door graden van de ecliptica die tegenover elkaar liggen.   Ook een herstelling is makkelijk langs deze weg: ik duid namelijk de cirkel aan waarop de significator staat, of de plaats waar de herstelling het begin neemt, en ik teken de plaats van de almuri aan op de rand; vervolgens draai ik het volvellum tot waar het eind van de herstelling op die aangeduide cirkel valt, en weer teken ik de plaats van de almuri op de rand; en dan tel ik de graden van de rand, bevat tussen die twee aangetekende plaatsen; omdat deze de graden van de herstelling zijn.

Over aspecten volgens de gemeenschap der astrologen en in het bijzonder volgens Albategni.

Er is ook een derde manier bij het opnemen van aspecten, die door zeer velen voor de eerste wordt gehouden, als zijnde door de meeste filosofen geautoriseerd, en die is met gelijke graden die zijn van de ecliptica, algemeen aanvaard. En dat dit waar is bevestigt Albategni in het vierenvijftigste hoofdstukje van zijn boek*); tenzij het hemellichaam waarvan het aspect wordt gezocht enige breedte heeft vanaf de ecliptica-lijn; zodat als het geen breedte heeft, meteen de graden van de aspecten zullen blijken. Als een hemellichaam namelijk staat in het begin van Ram, staat het op deze manier in zeshoeks-aspect ten opzichte van het begin van Tweelingen en het begin van Waterman. En evenzo met de andere aspecten, en dit met de afzonderlijke graden van de kring der Tekens; zoals blijkt in de volgende figuur.   *)  Albategni, De scientia stellarum, Bon. 1645, p. 208.

  d 3

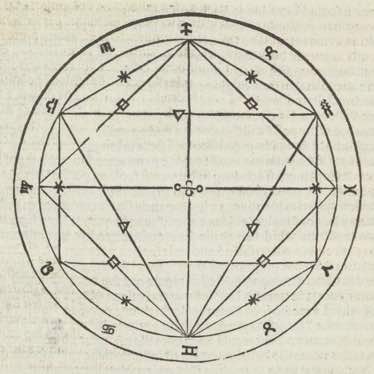	Tweelingen	Waterman
		Ram

Maar als een hemellichaam enige breedte heeft zal dit weinig uitmaken, ook als de breedte 10 graden zou kunnen zijn; omdat dit in de aspecten nauwelijks een verschil zou maken van 30 minuten van een graad; zoals kan blijken voor wie het beproeft. En dit komt alleen voor bij het zeshoeks-aspect en bij het driehoeks-aspect. De manier om zich de verschillende aspecten voor te stellen is namelijk bij deze toepassing als volgt, dat men zich moet voorstellen een grote cirkel gaande door het hemellichaam waarvan we het aspect zoeken, die de ecliptica-lijn snijdt in twee middens, op zo'n manier dat er vanaf één van die snijpunten tot aan het hemellichaam 60 graden zijn, de graden van die grote cirkel. En de graden van de ecliptica die er zijn vanaf datzelfde snijpunt tot aan de graad van de ecliptica waarop hetzelfde hemellichaam is in lengte (hoewel het in breedte erbuiten is) zijn de graden van de ecliptica die bij een zeshoeks-aspect behoren. En aangezien alle grote cirkels op de sfeer elkaar in gelijke delen snijden, is het noodzakelijk dat er vanaf dezelfde plaats van het hemellichaam tot aan het andere snijpunt 120 graden zijn, de graden van dezelfde grote cirkel; en vanaf de graad van dezelfde ster in de ecliptica tot aan dat tweede

[ d 3v ]

snijpunt zijn zoveel graden van de ecliptica omvat, als die van zijn driehoeks-aspect. Op deze manier kunnen we ons een dubbel zeshoeks-aspect voorstellen en evenzo een dubbel driehoeks-aspect. Een voorstelling van het vierkants-aspect kan echter volgens dit principe, hoe groot ook de breedte van het hemellichaam is, geen enkel verschil maken, aangezien 90 graden van de ecliptica aan beide kanten afgeteld altijd precies een dubbel vierkants-aspect zullen omvatten. De twee snijpunten van de ecliptica en de grote cirkel die door het hemellichaam gaat, moeten immers bij dit aspect verwijderd zijn van hetzelfde hemellichaam over 90 graden, van de graden van die grote cirkel. En evenzo van de graad van het hemellichaam in de ecliptica met evenveel graden van de ecliptica, dat wil zeggen 90. Beide genoemde snijpunten zijn immers polen van die cirkel die gaat door de polen van de ecliptica en door het hemellichaam en door de ecliptica, de plaats van het hemellichaam in lengte aangevend op de ecliptica. Maar opdat we dat verschil, hoe zeer gering en weinig belemmerend het ook is, dat door de breedte van de planeten optreedt, met een instrument heel gemakkelijk kunnen onderscheiden, zal ik hier iets anders toevoegen, dat nog op mijn instrument passend zou kunnen worden aangebracht op een kleine ruimte en met weinig lijnen of bogen. Maar omdat ik vond dat dit instrument in staat was om het werk te vervullen en bovendien van grote omvang en uitstekende vormgeving, daarom heb ik afgezien van deze aanvulling op dit instrument, ten gunste van het universele astrolabium dat met een andere naam saphea*) genoemd wordt.   Steeds als men dus met dit instrument de graden van een zeshoeks-aspect wil vinden op de al genoemde manier, moet afgeteld worden op de liniaal die over dit instrument wordt bewogen, in de verhandeling van dit instrument schuine horizon°) genoemd; moet afgeteld worden zeg ik, vanaf het midden van die liniaal waar de pin wordt geplaatst, naar één van de uiteinden ervan, zestig graden. En daar zet ik op de scherpe kant van die liniaal een merkteken en vervolgens beweeg ik deze liniaal zó, dat dit merkteken zover verwijderd is van de hemel-equator die op dat instrument beschreven is, als de breedte van het hemellichaam is, waarvan ik het aspect zoek — en dit door te tellen op de bogen die daar revolutiones°) worden genoemd, tot gelijk met de breedte van het hemellichaam; en die bogen staan op dat instrument voor de parallel-cirkels — en dan breng ik het merkteken over op de schijf. Daarna kijk ik naar de boog van de cirkel die de hemel-equator snijdt waarbij dat merkteken staat, of waarop — en deze bogen warden ascensiones°) genoemd in die verhandeling — en zoveel graden (en delen ervan) er zijn vanaf dit merkteken tot aan de diameter die komt vanaf de polen van de hemelequator-lijn, tellend met die bogen die ascensiones heten, zoveel graden van de ecliptica zullen overeenkomen met het gezochte zeshoeks-aspect van het hemellichaam; en zo'n zeshoeks-aspect is altijd kleiner dan 60 graden. En zoveel als het zeshoeks-aspect kleiner is dan zestig, zoveel is het driehoeks-aspect ervan groter dan 120 graden. Zodat het zeshoeks- en het driehoeks-aspect altijd vallen op tegenover elkaar liggende graden; en hetzelfde geldt voor beide zeshoeks- en voor beide driehoeks-aspecten. Dit zij dan gezegd over de aspecten.   Doch over het vinden van de graden van de ascendant van jaarlijkse omwentelingen, zowel die van de wereld als die van een geboorte, met dit instrument, zoals ook over andere veelsoortige zaken waarbij met ditzelfde instrument gewerkt zou kunnen worden,   Face of the Saphea     *)  Saphea: hemelequator staat vertikaal, NP is links. Zie Gunther 1976, p. 256-262, met verwijzing naar: Alfonso X, Libros del saber de astronomía, T. 3, 1864, 'Libros de la lamina universal', met fig. Rete en fig. Face. Figura de la red       Spaans manuscript, 1276/1278: BH MSS 156: Libro de la lamina, figura de la red, Libro de la azafeha, figura de la fas; index in Libros del saber, T. V, p. 103.   Gunther 1976, p. 159: "In 1263 Arzachel's treatise on the Saphea was translated into Latin by Profacius and Johannes Brixiensis, and a copy is preserved in Paris MS. latin, No. 7195.", met de tekst die ook te vinden is in Sédillot 1844, p. 185.   °)  Vorige noot, Sédillot 1844, p. 190: "regula recta ... est vice horizontis obliqui". P. 188: "arcus qui secant hunc diametrum [circuli horizontis recti] ... dicuntur revolutiones". (Horizon van de 'recta sphaera', plaats op de evenaar, polen op de horizon.) P. 189: "Arcus vero qui concurrunt in ipsis duobus polis describunt ascensiones circuli recti".

[ d 4 ]

aangezien die in verschillende verhandelingen voldoende zijn beschreven, leek het mij niet de moeite waard ze hier te herhalen. Voor zoveel als het is zal ik dan, met afkapping van verdere uitbreiding van het geschrift, hier een eind maken aan dit werkje. Moge dus, broeder Willem, dit kleine onvolwassen bedenksel van mij uw filosofisch onderscheidings­vermogen behagen. Opdat het u niet zou tegenstaan heb ik me erop toegelegd het zo beknopt samen te vatten, in de hoop dat u met uw grote en voortreffelijke verstand zou weten, dat ik het beter begrijp dan ik zelf zou kunnen beschrijven. Verder moet u beslist weten dat, als het nog in mijn vermogen zou liggen grotere dingen dan deze te doen, u mij daartoe bereid zult vinden, uit liefde voor uw welwillendheid. Moge uwe eerwaarde altijd gezond blijven en mij zo God wil volstrekt niet vergeten. Dit werkje is door Hendrik Bate voltooid in Mechelen, toen de Maan in conjunctie was met Jupiter, in het zevende huis, met de Leeuw als rijzend teken, in het jaar 1274 op 11 oktober; op verzoek van broeder Willem van Moerbeke, predikheer, penitentiaris van de paus en kapelaan.

[Equatorium planetarum].*)

Als we de ware plaatsen van de planeten juist willen vaststellen met het door ons speciaal hiervoor bedachte instrument, gaan we als volgt te werk. Aangezien daar één cirkel is die te plaatsen is in verschillende liggingen, en weer verplaatsbaar, die de gemeenschappelijke functie van equant°) vervult voor vijf planeten, namelijk Saturnus, Jupiter, Mars, Zon en Venus: Als het gaat over de Zon, plaatsen we dat deel van deze cirkel waar geschreven staat aux#) volgens het gat waarboven geschreven staat aux Solis; en de tegenover­gestelde kant in het gat er­tegenover. Dan dus, als beschouwd wordt de hoek van de Zon op een gegeven tijdstip, afgelezen uit de tabellen van Toledo of gelijke die op de achtste sfeer zijn gebaseerd, zetten we een gelijk getal op deze equant-cirkel, en wel vanaf het apogeum beginnend, als merkteken daar waar de telling eindigt. Daarna spannen we een draad vanaf het middelpunt, dat met een pin is vastgemaakt aan het midden van het instrument, en we trekken deze recht door het merkteken dat op de equant-cirkel is aangegeven, tot aan de kring van de Tekens, die de rand van het instrument is; en de plaats waar de zo gespannen draad de rand snijdt is de ware plaats van de Zon op de achtste sfeer. Dit instrument is namelijk bedacht en gebouwd op grond van de planeet­bewegingen ten opzichte van de achtste sfeer, volgens welke Arzachel en zoveel andere waarnemers hun tabellen hebben gegrondvest; zoals blijkt in de tabellen van Toledo, die van Novara, Hereford en veel andere. Ptolemaeus echter, en Geber, Albategni en Abraham ibn Ezra, Al-Sufi en ook andere meesters van de waarneming, vooral astronomen in het Oosten, die de planeet­bewegingen ten opzichte van de negende sfeer beschouwden, hebben zich hierop gebaseerd. En dit blijkt in   Lussen van Mars   *)  This short text describes the uses of an equatorium, an instrument which allows one to find the position of the planets mechanically and without calculations (Steel 2018, p. 44). North 2005, p. 61: albion, een 'equatorium';  Falk, 'A Merton College Equatorium', 2016. Willem Gilliszoon, Liber desideratus super coelestium motuum indagatione sine calculo, Lyon 1494 (facs. ed. D.J. Struik, 1965). Johann Schöner, Aequatorium astronomicum, 1521;  Canones, 1522. Francisco Zarzoso, In aequatorem planetarum libri duo, 1526.   °)  Verhelderende figuren in: James Evans, 'Fonction et origine probable du point équant de Ptolémée', 1984. Lussen van Mars (zie figuur), tussen 1971 en 1984, worden aangepast met de equant van Ptolemaeus. Vergelijk de figuur van Joh. Kepler in Astronomia nova (1609), p. 4: lussen van Mars, 1580 - 1596.   #)  Aux: "the geocentric 'Aux' is similar (but not equal) to the heliocentric Apogee" (Price 1955, p. 109).

[ d 4v ]

de tabellen van Ptolemaeus, Albategni en Abraham, in de de tabellen van Pisa, Winchester*) en andere; daarom hebben zij ook hun beoordelingen hiernaar gegeven; zoals vooral blijkt bij de prins van de judiciële astrologie Albumazar. En dezen hebben allen de beweging van de achtste sfeer verschillend van de vorigen gesteld; dezen hebben die namelijk gesteld als eenparig om de polen van de ecliptica, de anderen daarentegen hebben zich kleine cirkels om het begin van Ram en Weegschaal voorgesteld. En hoewel dit instrument van ons is gegrondvest op de achtste sfeer, is het niettemin geldig voor de planeet­bewegingen, aangepast aan deze tweede methode die volgens de negende sfeer is.   Dus als we liever langs deze tweede weg de plaats van de Zon willen vinden uit tabellen die hiervoor zijn opgesteld, zoals die van Mechelen°), of die van Pisa, moeten we de hoek van de Zon nemen en verder is de behandeling in alles op die manier die ik eerder heb uiteengezet. En de zo gevonden plaats van de Zon noteren we zorgvuldig in de kring van de Tekens en die bewaren we voor wat we zullen beschrijven. Vervolgens halen we het apogeum van de Zon in de achtste sfeer, zoals het in de tabellen van Toledo of andere gelijke wordt gesteld, af van het apogeum van de Zon volgens de negende sfeer, overeenkomend met het gegeven tijdstip. En de rest tellen we op bij de al gevonden plaats van de Zon waarvan ik voorschreef die te bewaren; en zo hebben we het gevraagde. Bij voorbeeld: het apogeum van de Zon in de achtste sfeer is twee Tekens en 17 graden en 50 minuten. Het apogeum van de Zon in de negende sfeer echter is voor de gegeven tijd twee Tekens en 29 graden en 13 minuten. Van dit laatste aantal moeten we dus het voorgaande aftrekken, en overblijft elf graden en drieëntwintig minuten, welke graden en minuten we optellen bij de volgens de genoemde manier gevonden en bewaarde plaats van de Zon; en dit is het gevraagde. Ook moet er op gelet worden dat de achtste sfeer beweegt, volgens de latere meesters van de waarneming eenparig met één graad in 70 jaar. En de apogea van de planeten volgen deze beweging, en daarom worden deze apogea volgens wat de tijd vereist gerectificeerd ten opzichte van de negende sfeer, en wel voor elke 70 jaar met één graad, en voor honderd met een graad en 25 minuten, en voor 20 jaar met 17 minuten, en voor één jaar met 51 seconden. En zo behoort die toevoeging waarvan ik nu een voorbeeld heb gegeven voor het betreffende tijdstip te worden vastgesteld.

Over de vereffening van Saturnus, Jupiter, Mars en Venus met het instrument.

Maar als we nu de plaats van Saturnus in de achtste sfeer met dit instrument willen onderzoeken, moeten we als volgt te werk gaan. Die verplaatsbare cirkel die dient voor de equant plaatsen we op zijn manier ten opzichte van het apogeum van Saturnus, dat op het instrument geschreven is zoals ik heb voorgeschreven dat het bij de Zon wordt gedaan. We brengen ook de epicykel van Saturnus aan, als volgt: die ronding of het rondje dat aan het einde van de plaat van de deferens zit stellen we als epicykel, zodanig dat het gat dat erin is gemaakt in de richting zit van het gat van het hoofd­middelpunt van het instrument, en we draaien dit rondje zó, dat het middelpunt van de equant van Saturnus dat op dat rondje is aangegeven recht in de richting van het apogeum van Saturnus valt; dan zal het rondje vanzelf op zijn plaats vallen, omdat een pinnetje dat aan de onderkant van het rondje bevestigd is in het ervoor bestemde gaatje komt; en dan wordt   *)  Wintoniensibus: van Winchester. Zie North 2002, p. 13; North 2005, p. 241: "Abraham Ibn Ezra ... a new set of astronomical tables he composed. He adapted them to at least two of his places of residence, Pisa and Winchester".   °)  Machlinenses: van Mechelen, eigen werk van Hendrik Bate. Zie Steel 2018, p. 46.

[ d 5 ]

het rondje vastgezet met de grote pin, die midden op zijn kop het middelpunt van de kring der Tekens draagt. En dit alles blijkt gemakkelijk door alleen het instrument goed te bekijken. Als dan uit de tabellen van Toulouse of daaraan gelijke het middelpunt van Saturnus*) is gehaald, tellen we, beginnend bij het apogeum van de equant, een gelijk aantal af op die equant-cirkel, in de volgorde van de verdelingen; en waar het aantal bereikt is wordt een teken gezet. Daarna wordt een draad gespannen vanaf het middelpunt van de equant, dat in het rondje gegrift staat, tot in het teken dat op de equant is gezet; en onder deze zo gespannen draad wordt de epicykel gedraaid, zodanig dat het apogeum ervan en het tegengestelde apogeum van de epicykel er recht onder vallen. Als we ook beschouwen de gemiddelde hoek van Saturnus, met tabellen gevonden, gaan we een gelijk aantal aftellen op de epicykel van Saturnus, en waar de telling eindigt brengen we het tongetje dat over de epicykel draait op zijn plaats, terwijl de epicykel onbeweeglijk in rust blijft. Dan moet de draad weer opgenomen worden en gespannen vanaf het middelpunt van de pin, recht door het teken op het tongetje, en tot in de kring der Tekens gehouden; en de plaats in de kring der Tekens die de draad aanwijst is de ware plaats van Saturnus in de achtste sfeer.   Als we ons werk echter willen veranderen volgens de tweede leerschool, en de plaats van Saturnus met ons instrument vereffenen volgens de principes van deze school, halen we het middelpunt en de hoek van Saturnus uit de tabellen van Mechelen of van Pisa of gelijke, die volgens de negende sfeer lopen; en verder gaan we geheel te werk op dezelfde manier die ik over Saturnus net heb uiteengezet. En nadat de plaats van Saturnus in de kring der Tekens op deze manier is gevonden, wordt hij zorgvuldig bewaard. En tenslotte moet daarbij dezelfde optelling worden gedaan die ik eerder heb gesteld bij het voorbeeld over de Zon.   Nu de instructie van de vereffening van Saturnus met het instrument behandeld is, blijkt voldoende hoe de instructie is voor de vereffening van Jupiter, Mars en Venus met hetzelfde instrument. De manier van werken is immers geheel gelijk, nadat we de equant-cirkel in de vereiste stand hebben gezet voor welke men wil; en de epicykel brengen we voor elk op de passende manier aan; elk heeft namelijk zijn eigen epicykel, zoals blijkt op het instrument.   Vermeld moet nog worden dat, wegens de geringe afstand van het middelpunt van Venus tot het middelpunt van de kring der Tekens, het noodzakelijk was dat het middelpunt van diens equant op de pin van ons instrument valt. Daarom moet er bij het vereffenen van Venus zorgvuldig op gelet worden dat de pin van het instrument zó wordt geplaatst dat dit eccentrische middelpunt recht onder het apogeum van Venus draait, zonder ook maar een kleine slordigheid. Zo is dan duidelijk wat er met ons vrij grote instrument gedaan moet worden bij de vereffening van vijf planeten.

Over Mercurius.

Maar omdat we voor Mercurius en de Maan een speciaal instrument hebben, omdat hun bewegingen niet passen bij die van de vorige, daarom moet een speciale instructie gegeven worden over de manier waarop we ermee te werk moeten gaan om ook hun plaatsen te vereffenen. Als we dan Mercurius willen vereffenen, bekijken we de zijde van het instrument die voor Mercurius dient. Dit instrument heeft namelijk   *)  Lat.: centro Saturni, middelpunt van de epicykel. Even hierna: "de gemiddelde hoek van Saturnus" (Lat.: argumentum Saturni). Poulle 1994, Table 3: "medius cursus Saturni".

[ d 5v ]

twee zijden, waarvan de ene dient voor Mercurius en de andere voor de Maan. Laten we dus eerst het middelpunt van Mercurius nemen, zoals het wordt gevonden met tabellen die volgens de achtst sfeer lopen. Als we vervolgens de zijde van het instrument bezien die staat voor Mercurius, vinden we de rand ervan weer verdeeld volgens de twaalf Tekens van de Dierenriem; en op dezelfde zijde onmiddellijk binnen de rand vinden we een andere cirkel met zijn verdelingen en opschrift van getallen die geheel onbeweeglijk is; en dit is de equant-cirkel van Mercurius. En binnen deze equant is er een andere, in het andere oppervlak beweeglijk en draaibaar, met zijn verdelingen en voorzien van de nodige getallen; en deze cirkel heet de cirkel van het beweeglijke apogeum. En binnen deze cirkel draait een ronde schijf, de deferent, die de epicykel van Mercurius meevoert. We vereffenen Mercurius dan als volgt: volgens het getal van het middelpunt van Mercurius, vooraf uit tabellen genomen zoals gezegd, tellen we het aantal af op de cirkel van het beweeglijke apogeum, beginnend bij het apogeum ervan, in de daar beschreven volgorde; en waar het aantal bereikt is zetten we een merkteken. Vervolgens wordt de cirkel zó gedraaid, dat dit merkteken recht onder het apogeum van de onbeweeglijke equant valt; en dan wordt deze cirkel vastgezet met was of iets anders, zodat hij niet heen en weer kan bewegen. Daarna tellen we volgens hetzelfde middelpunt van Mercurius op de equant-cirkel, beginnend bij het onbeweeglijke apogeum ervan, in de volgorde van zijn verdelingen en getallen, en waar deze telling eindigt komt een merkteken. Dan wordt een draad gespannen vanaf dit merkteken tot in het middelpunt van de equant, dat naast het hoofd­middelpunt van het instrument blijkt te zijn, en de schijf die de epicykel meevoert wordt gedraaid totdat het middelpunt van de epicykel en het apogeum ervan en eveneens het tegengestelde apogeum recht onder deze draad vallen. En daarna gaan we op de epicykel, en wel op de buitenste cirkel daarop beschreven, aftellen het gedeelte van Mercurius, oftewel de hoek, die gehaald is uit de betreffende tabellen; en we tekenen aan waar het eindigt. En tenslotte spannen we een draad vanaf het hoofd­middelpunt in het midden van het instrument, en door het aangetekende op de buitenste cirkel van de epicykel, tot aan de rand van het instrument; en de plaats van de draad op de rand is de ware plaats van Mercurius in de achtste sfeer.   Maar als we de andere leerschool willen volgen, ten opzichte van de negende sfeer, dan gaan we te werk zoals ik bij Saturnus heb uiteengezet.

Over de Maan.

Als we daarentegen de Maan willen vereffenen, bekijken we de zijde van dit instrument die voor de Maan gemaakt is. En daar verschijnt een nauwkeurige voorstelling van de bewegingen van de Maan volgens wat door de meesters van de waarneming is gevonden en bedacht. De gemiddelde plaats van de Zon, uit tabellen gehaald, tekenen we aan op de rand; als daarna de hoekafstand van de Maan tot de Zon, volgens de gemiddelde loop, genomen wordt uit hiertoe gemaakte tabellen, moet afgeteld worden op de cirkel die onmiddelijk binnen de rand draait, en die de cirkel van het apogeum van de Maan is; moet afgeteld worden, zeg ik, en wel beginnend bij het apogeum, in de volgorde van de erop geschreven getallen, zoveel Tekens, graden en minuten als de hoekafstand van de Maan tot de Zon is; en de aangetekende graad waarin die telling eindigt moet geplaatst worden onder het teken van de gemiddelde

[ d 6 ]

beweging van de Zon. En dan zet ik deze cirkle vast, zodat hij niet heen en weer kan bewegen. Vervolgens ga ik op dezelfde cirkel van het apogeum weer aftellen vanaf het eind van het eerste getal, zoveel als de hoekafstand van de Maan is van zichzelf; en dit is het dubbele van de hoekafstand van de Maan tot de Zon; geteld moet worden op de cirkel van het apogeum vanaf het apogeum ervan. En dan span ik een draad vanaf het middelpunt van de rand, dat is het middelpunt van de kring der Tekens, tot op de plaats waar de telling eindigt op de cirkel van het apogeum. Daarna draai ik de schijf die de epicykel meevoert, totdat het middelpunt van dezelfde epicykel onder deze draad valt. Dan moet deze schijf onbeweeglijk blijven. Maar de draad verplaatsen we naar het middelpunt dat ligt tegenover het middelpunt van de deferent van de Maan, en vanaf dit middelpunt spannen we de draad recht door het middelpunt van de epicykel en verder; en onder deze draad plaatsen we het apogeum en het tegenovergestelde van het apogeum; en alle schijven van het instrument moeten onbeweeglijk blijven. Dit middelpunt nu, vanwaar de draad wordt gespannen, is dat kleine gaatje dat draait om het rondje dat in het midden van het instrument is geplaatst. Het middelpunt van de deferent echter, dat op dezelfde manier draait, heb ik met opzet dichtgestopt, opdat het middelpunt er tegenover duidelijker zou uitkomen. Hierna dan, met de hoek van de Maan uit tabellen gehaald, ga ik volgens de grootte ervan de Tekens en de graden aftellen op de epicykel van het instrument; en ik plaats het tongetje dat over de epicykel draait gelijk met de hoek van de Maan. En tenslotte span ik een draad vanaf het hoofd­middelpunt dat in het midden van het instrument is, door het midden van het kruisje dat op het tongetje van de epicykel is gegrift, tot op de rand van het instrument. En de plaats van de draad op de rand is de ware plaats van de Maan. Hierbij moet ook begrepen worden dat, volgens welke weg we de Maan ook willen vereffenen, of het nu is volgens de achtste sfeer of volgens de negende, en met welke tabellen we het middelpunt van de Maan en de hoek ook nemen, steeds is er één manier van werken op ons instrument.   Hier eindigt naar wens het werkje van Abraham ibn Ezra over Horoscopen met voorbeeld­figuren voor de afzonderlijke huizen. En de bouw van het Astrolabium van Hendrik Bate volgens de meester. Gedrukt te Venetië door en op kosten van Erhard Ratdolt van Augsburg. In het jaar van de zaligmakende menswording van onze Heer 1485, op 24 januari.

Bronnen en literatuur