Betoog , breedte en lengte , breedte meten , lengte meten , tekens (geluid, licht, maan-eclips) , onvolmaakt ,
andere middelen (maanbaan, zon-eclips, klok) , ook onvolmaakt , beste , volmaaktheden , nut
| Betoog over het vinden van Oost en West |
| Daar de ganse Aardbodem die wij bewonen, samen met de Zeeën een ronde bol maakt, en onze blik daardoor maar een een klein gedeelte ervan kan omvatten, komen we nooit tot volmaakte kennis van landen en provincies zonder ons te verplaatsen en alles van dichtbij te gaan waarnemen. Doch omdat dit niet voor iedereen mogelijk is hebben verstandige geesten van oudsher getracht ze in Kaarten af te tekenen. Hieruit is gesproten de heerlijke wetenschap of kunst genaamd GEOGRAFIE, dat is landbeschrijving, in onze eeuw door de grote zeevaart en de koophandel bijna tot volmaaktheid gebracht. Om nu landen en steden op Kaarten te plaatsen zoals ze op de Aardbol liggen, is bevonden dat twee middelen noodzakelijk zijn: kennis van de ware breedte en van de echte lengte, dat wil zeggen van het ware Zuiden en Noorden, en van het Oosten en Westen van plaatsen. Ook zijn daartoe hulpmiddelen bedacht: instrumenten en de manieren om ze te gebruiken. |
|
Eerst willen we beschrijven wat dat is, de ware breedte of Zuid en Noord, en de ware lengte, of Oost en West. Over de breedte en de lengte van steden, noord en zuid, en oost en west Door de hemelmeters is bevonden dat de Aardbol rond is en in het midden van de hemel staat. Dus hebben ze alle cirkels aan de hemel bedacht die nodig zijn om de loop van de sterren beter te kunnen onderscheiden en berekenen. De hemel draait één keer rond in 24 uur, van oost naar west, dus ze hebben besloten dat de beweging gaat om een bepaalde As, met aan de uiteinden twee punten die stilstaan aan de hemel; zoals er bij een houten bol, op twee ijzeren punten draaiend, altijd twee zwarte putjes in het hout achterblijven. Deze punten zijn genoemd Aspunten of Polen, dat wil zeggen draaipunten; er is een Noordpool en een Zuidpool. Bovendien was er de gewaarwording dat de hemel en de sterren bij de Polen langzamer omliepen en minder weg aflegden dan bij het midden van de hemel. Dat dus elk punt aan de hemel een eigen cirkel beschrijft, en een punt dat even ver is van beide polen moest de grootste cirkel maken. Deze cirkel bepaalt het midden van de hemel en ze hebben hem genoemd Æquinoctiaal (Equator), omdat de Zon, als hij in zijn loop in de Zodiak (Dierenriem) op deze cirkel komt, de dag en de nacht even lang maakt in de hele wereld. Verder, omdat de Zon en alle sterren dagelijks boven de Horizon verschijnen, in het Oosten, en de hoogte toeneemt tot aan het hoogste punt, pal Zuid of Noord, en dan weer afneemt, |
|
tot de ondergang in het Westen, hebben de Hemelmeters nog een cirkel bedacht, door de polen en door ons Zenit recht boven ons hoofd, die deze op- en ondergang in twee gelijke delen verdeelt (voorzover deze cirkels boven de horizon uitsteken). Deze cirkel hebben ze genoemd de Meridiaan, dat is middagcirkel. Deze cirkels nu, samen met de As en de polen van de hemel, worden ook op de Aardbol gesteld, die hetzelfde middelpunt heeft. Wij hebben op aarde dus ook twee polen, een noord- en een zuidpool, onze Æquinoctiaal of middellijn (evenaar), en het punt van ozne woonplaats dat met ons Zenit aan de hemel op een loodrechte lijn staat. De evenaar op aarde is enig en onveranderlijk, doch er zijn talloze verschillende meridianen: te trekken door de polen van de aarde en onze verblijfplaats. Een meridiaan kan dus wel door verschillende plaatsen op de aardbol gaan als ze zuid en noord van elkaar liggen, maar als ze oost en west van elkaar liggen, of een andere streek dan zuid en noord, hebben ze altijd verschillende meridianen. Om nu te zeggen wat dat is, de breedte of lengte der steden zuid en noord, is te weten dat onder de breedte van een punt op de aardbol wordt verstaan een stuk van de meridiaan daarvan, gerekend vanaf de evenaar tot de plaats van dat punt, noordelijk of zuidelijk. |
| Dit kunnen we verklaren met de volgende figuur, waarbij we ook uitleggen wat gezegd is over de meridiaan, as en polen. |

|
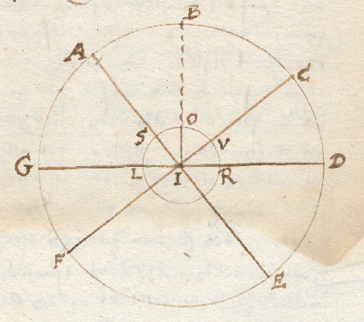
De cirkel ABDG stelt voor de uiterste omtrek van de hemel, en ORMS*) de aardbol, met samen het middelpunt L, volgens de algemene opvatting van de hemelmeters. Laat iemand op aarde wonen in O, met als horizon de lijn GD, door L, al is de woonplaats O, want de lijn IO is zo klein ten opzichte van de grote afstand ID van hemel tot aarde, dat het niet uitmaakt. De hemel draait van oost naar west, en heeft de polen A en E, dus zal de Eqiuinoctiaal midden daartussen komen: CIF, en AE is de as van de wereld. De woonplaats is in O, en de lijn IOB, loodrecht op de horizon GD wijst naar het toppunt of zenit B, en de cirkel ADEF is de meridiaan aan de hemel van O. Zo worden al deze cirkels en punten ook waargenomen op de aardbol: - woonplaat O komt overeen met zenit B, - S is de noordpool van de aarde, N*) de zuidpool, SN de as van de aarde, - VM is de evenaar, en de cirkel SRMS de meridiaan van O op aarde. Dus wanneer een stad of eiland recht onder de Eqiuinoctiaal CVF van de hemel ligt, of op de aardse VIM, te weten in V, is er geen breedte. En zo'n ligging heeft onder andere het vermaarde eiland Sao Tomé. Maar wanner een plaats afwijkt van de evenaar,
*) In de figuur ontbreekt M, onder L op de evenaar CF. En ook N, aardse zuidpool op AE. |
|
naar een van de polen S of N, zoals hier O naar S, zegt men dat de breedte is: het deel van de meridiaan VO tussen de evenaar V en O, met de naam van de pool erbij, zoals hier een noordelijke breedte. Alle plaatsen die op hun eigen meridiaan even ver van de evenaar liggen, hebben een bepaalde noordelijke of zuidelijke breedte, ze liggen op een cirkel die evenwijdig is met de evenaar, een parallel-cirkel. Tot zover de breedte. Uit het voorgaande kan de lengte gemakkelijk begrepen worden. Plaatsen die buiten een meridiaan van elkaar liggen, hebben meridianen die meer of minder verschillen. Oost en West is dus niets anders dan dit verschil. Alle meridianen komen samen in de pool en snijden de evenaar en de parallelcirkels, dus op elke parallel kan men berekenen hoeveel graden en minuten twee steden ten oosten of westen van elkaar liggen. Doch omdat ze op de evenaar het verst van elkaar zijn gescheiden, wordt het verschil der meridianen gewoonlijk berkend op de evenaar. Dit geldt voor Oost en West in het algemeen. Maar om de eigen lengte van plaatsen op de aardbol te bepalen, is te weten dat de ronde aardbol geen begin en einde heeft, zodat aan de wetenschap de vrijheid is gelaten, zo'n begin der lengte te kiezen. De Ouden hebben dit begin, of de eerste meridiaan, gesteld op een der Canarische eilanden, |
|
zoals die ook nog gesteld wordt op het eiland Teneriffe, door de vermaarde hoge berg Pico del Teide. Van deze meridiaan oostwaarts langs de evenaar, totdat men komt aan de meridiaan van een bekende plaats, in graden en minuten, dat is de lengte van die plaats. En vervolgens telt men over de hele aardbol tot 360 graden op de evenaar, als men weer bij de eerste meridiaan van Teneriffe is. Het aantal graden en minuten van de evenaar tussen de meridianen van twee plaatsen, is het lengteverschil van die plaatsen, die elk hun eigen lengte hebben ten opzichte van de meridiaan van Teneriffe. De reden waarom de Ouden dit de lengte hebben genoemd, en het voorgaande de breedte, is dat op hun Kaarten de landen zich ongeveer 90 graden uitstrekten naar noord en zuid, en ongeveer 180 graden naar oost en west; ze kenden dus een langwerpig vierzijdig stuk land. Voor hen was de wereld niet verder bekend dan tot 60 graden noorderbreedte en 30 graden zuiderbreedte, en de lengte strekte zich uit van de meridiaan van de Canarische eilanden tot de uiterste eilanden van Indië in het oosten. Om de lengte en breedte van steden nog beter te begrijpen zal ik hier een figuur bij doen, die de halve aardbol weergeeft op een plat vlak. Hetzelfde is te begrijpen van de hele aardbol in het rond. |
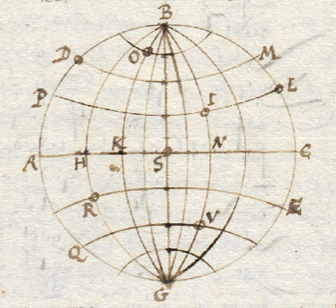
| Laat B en G de polen van de aarde zijn, AC de evenaar. |
|
west is bij A, noord bij B, oost bij C, zuid bij G. Er zijn verschillende plaatsen zoals D, O, I, R, V, S, waarvan D genomen is voor Teneriffe (de meridiaan ervan is BAGC). Bij A op de evenaar is het begin der lengte, Teneriffe heeft lengte 0 en breedte AD, noordelijk. Neem nu de stad O: de lengte is die tussen de meridianen BAG en BOKG, dus AK; de breedte is KO, noordelijk. Zo heeft de stad I lengte AN, breedte NI. De stad S ligt op de evenaar en heeft geen breedte, de lengte is AS. Evenzo zal stad R de lengte AH hebben en zuiderbreedte HR. Tenslotte zal stad V de lengte AN hebben (dezelfde als I) en zuiderbreedte NV. Als twee steden zoals I en L op eenzelfde parallel PIL liggen, even ver van de evenaar, hebben ze eenzelfde breedte NI of CL. Op verschillende parallellen, zoals D en I, verschillen ze in breedte zoals PD of LM, in graden en minuten. |

|
Als twee steden op één meridiaan liggen, zoals V en I, is er geen verschil in de lengte, maar alleen in de breedte, zoals het stuk bestaande uit NI en NV. Als ze op verschillende meridianen en parallellen liggen, zoals R en I, verschillen ze in lengte (HN) en breedte (EL), enzovoorts bij alle liggingen van landen en steden of eilanden in zee. Hetzelfde is ook te begrijpen van schepen op zee. |
|
Omdat de breedte het makkelijkst en betrouwbaarst gevonden kan worden zullen wij deze eerst behandelen. Te weten is, dat de breedte van landen precies overeenkomt met de hoogte die de hemelpool heeft boven de horizon van elke plaats, door het middelpunt van de aarde. Deze hoogte is niets anders dan een deel van de meridiaan van die plaats, tussen de pool en de horizon in het noorden of zuiden. Dus indien men de poolshoogte kan meten, weet men ook de breedte van de plaats, vanaf de evenaar. De poolshogte wordt op verschillende manieren gevonden. Doch eerst zullen we bewijzen dat die even groot is als de breedte. Laat in de figuur hier onder ABCD zijn de meridiaan aan de hemel, en de noordpool van de wereld E, de zuidpool O, de lijn EPO de as van de wereld, door het middelpunt P van de aarde. Laat de Equator van de hemel zijn FPN, de aarde IML, en daarop een stad in I. De noordpool G, de zuidpool Q; de horizon van de stad I is APC, en het toppunt of zenit is B. Nu zal op aarde de meridiaan van de stad I zijn LIMQ, en de evenaar HPK, dus de breedte van de stad I is de boog van H tot I. |
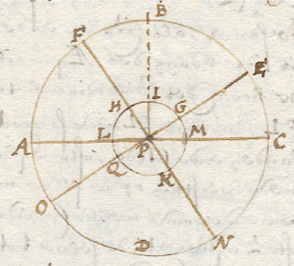
| De hoogte van de pool E zal zijn het meridiaandeel EC vanaf de horizon in het noorden C tot de pool E. Nu is te weten dat er in cirkels om eenzelfde middelpunt |
|
altijd gelijke delen gemaakt worden door dezelfde delende rechte lijnen, zodat GM evenveel doet in de meridiaan IML, als EC in de meridiaan ECOF, en HI evenveel op aarde als FB aan de hemel. Ook is op te merken dat de bogen van een cirkel evenveel graden en minuten inhouden als de hoeken van de rechte lijnen die op het middelpunt vallen, zodat de hoek EM*) gelijk is aan de boog EC, en de hoek FBP°) aan de boog FB. Waaruit volgt dat de hoek EPC gelijk is aan de hoogte van de pool CE, en de hoek FPB aan de boog FB, of HPI aan HI. Ik zeg dan dat HI even groot is als MG, of FB even groot als EC, dat wil zeggen: de breedte van de stad I is even groot als de hoogte van de pool E boven de horizon AC. Want: 1. de kwartcirkel BC is gelijk aan FE, en de rechte hoek IPM is gelijk aan HPG. 2. boog BE zit in beide kwartcirkels, en hoek IPG in beide rechte hoeken. 3. als men van gelijke grootheden hetzelfde aftrekt, blijft wat overschiet ook gelijk. Dus als BE wordt afgehaald van FE of BC, en de hoek IPG van HPG of IPM, blijven de bogen FB en EC gelijk, en de hoeken HPI en GPM, of de breedte HI van stad I met de hoogte van de pool G boven de horizon LM, of van de hemelpool E boven de horizon AC. Wat te bewijzen was.
*) Lees: GPM in plaats van EM. °) FPB in plaats van FBP. De poolshoogte is dus te vinden op twee manieren: met de hoogte van de evenaar (AF in de vorige figuur), en door meting met sterren bij de pool als ze op de meridiaan komen, in het bijzonder met de noordster (Poolster).
Doch indien men door meting weet hoe ver enige ster in het noorden van de pool af staat, is het al genoeg zijn kleinste hoogte AB te nemen en BC erbij te doen, |
|
zijn afstand van de pool, om de verlangde poolshoogte AC te krijgen; of zijn grootste hoogte DA, en de afstand van de pool DC er af te trekken. Om de hoogte van de evenaar te vinden moet men weten hoe ver eenige heldere sterren en de zon dagelijks afwijken van de evenaar, naar het noorden of zuiden; deze afwijking noemt men de declinatie. Als deze bekend is neemt men de hoogte als ze op de meridiaan zijn, en doet men de declinatie erbij, of trekt die er af, dan blijft over de hoogte van de evenaar. We bespreken verschillende gevallen aan de hand van figuren: dichtbij de evenaar of ver er vandaan. |
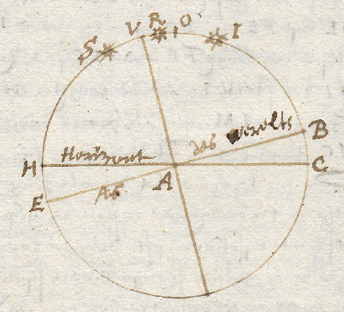
|
Hier valt het toppunt O bij de Equator VA, en de Zon staat in I, in de richting van pool B, of in S. Als de zon in I is, meet men zijn hoogte van C tot I en trekt men eraf de boog IB (het verschil van de kwartcirkel VB en de zonsdeclinatie VI), de poolshoogte is dan CB. Maar als de zon in R is, meet men zijn hoogte van H tot R en trekt men de de declinatie VR er af, dan is HV de hoogte van de Equator. Met de zon in S neemt men zijn hoogte HS en doet de declinatie SV erbij om HV te vinden. 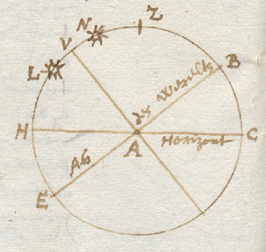
Hier staat de Zon buiten het toppunt Z, in de richting van pool E. Als hij in N is, is zijn hoogte HN, waarvan zijn declinatie VN wordt afgetrokken om de hoogte HV van de Equator te krijgen. Maar als de zon in L is, neemt men zijn hoogte HL, en doet men zijn declinatie LV daarbij, dat geeft ook de hoogtee HV. |
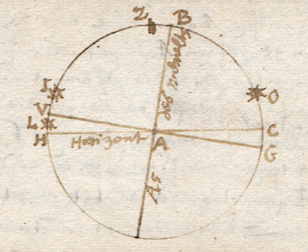
|
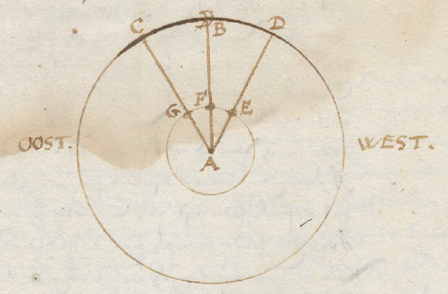
volmaakt overeenkomen met de meridianen aan de hemel, zoals ook de aardse evenaar met de hemelse Equator, volgt ook dat het lengteverschil van twee steden te vinden is uit de hemelequator en het verschil tussen de twee hemelmeridianen van deze steden. De hemelequator is de tijdmeter, die door eenmaal om te draaien een Etmaal maakt, oftewel een natuutlijke dag van 24 uur. Per uur passeren 15 graden van de Equator onze meridiaan, en per minuut passeren 15 minuten daarvan, enzovoorts. Het verschil op de Equator van twee hemelmeridianen van twee steden moet gevonden worden uit het tijdverschil tussen de twee steden. Aangezien de zon van oost naar west gaat, komt hij altijd eerder aan de hemelmeridiaan van plaatsen die ten oosten van ons liggen, dan aan die van steden ten westen van ons. Als wij hier middag hebben (12 uur), is het bij oostelijke volken namiddag, en bij westelijke voormiddag, enzovoorts. Bij voorbeeld: Laat ons in de figuur nemen dat drie steden A, B en C op één parallel liggen, |
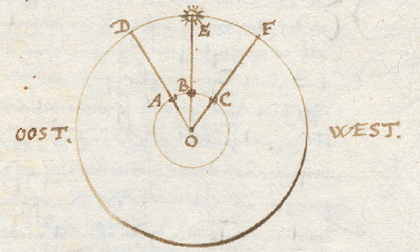
| dat wil zeggen op één breedtecirkel, of ook |
|
op de evenaar zelf (want we hebben al gezegd dat het niet uitmaakt waarop men de lengte van plaatsen berekent). Laat ze elk 30 graden op de evenaar van elkaar verschillen. De hemelequator is DEF, de evenaar ABC, de hemelmeridianen zijn OD, OE en OF, de aardse OA, OB en OC; de zon staat in E. Omdat nu de meridiaan OE overeenkomt met de meridiaan OB, is het middag in de stad B. Maar in C kan het nog geen middag zijn, omdat de zon nog niet op de meridiaan OF is gekomen; er zijn nog 30 graden te gaan, dat is 2 uur, dus het is tien uur in C. In de stad A is de zon de meridiaan OD al gepasseerd, en het is daar 2 uur na de middag. Als de zon vertrekt van de meridiaan OE, wordt het in B namiddag, maar ergens naar C toe wordt het dan middag. Wat hier verklaard is over de middag, moet ook zo begrepen worden van alle uren van de dag; dus als het 8 uur is in B, is het 10 uur in A, en 6 uur in C, enz. Alle steden onder één meridiaan OB hebben tegelijk middag en benoemen voor- of namiddag met dezelfde tijd. Nu genoeg bewezen is dat het verschil van twee aardse meridianen AO en OB of OC niet anders te vinden is, dan met het tijdverschil op eenzelfde ogenblik tussen twee plaatsen waarvan met het lengteverschil wil weten, wordt gevraagd met welk middel men tot kennis van dit verschil zou kunnen komen. Antwoord: dit is juist waar alles op aankomt, en daarom moet het nader verklaard worden; wat ik zal doen met onze stad Amsterdam in B, als het daar middag is. Men kan op elke tijd, overdag aan de Zon, 's nachts aan de sterren, met instrumenten voor het meten van de hemel precies de uren en minuten daarvan vinden en berekenen; dat zal iedereen toegeven die slechts iets weet van de Sterrenkunde. Dus ik zeg dat, als het net middag is in plaats B, indien men dan |
|
op hetzelfde ogenblik alle mensen, zowel oostelijk naar A, als westelijk naar C, met enig teken kon waarschuwen om ook hun tijd op te nemen aan Zon of sterren, met goede instrumenten, dat men dan door vergelijking zou weten hoeveel hun meridianen van de onze verschillen. Want uit het voorgaande blijkt dat de uurmeter in A twee uur later zou vonden, en de meter in C twee uur vroeger. Waaruit men dan ook zou besluiten dat de stad A 30 graden ten oosten van Amsterdam ligt, op de evenaar of op de parallel CBA; en de stad C zoveel graden westelijk. En zo zou men rondom de hele aardbodem de lengte bekend krijgen, tot aan de meridiaan van Amsterdam onder de aarde, waar het middernacht zou zijn, bij een lengteverschil van 180 graden. En als iemand op Teneriffe was geweest, zou men niet elleen de ware lengte van Amsterdam hebben verkregen, maar vervolgens ook van alle andere plaatsen, door optelling of aftrekking van de in elke stad gevonden lengteverschillen. Nu moet onderzocht worden wat voor tekens men elkaar kan geven op aarde, waarvan men verzekerd kan zijn dat de meting op een bepaald ogenblik gebeurt. Ze moeten zodanig zijn dat dat ze in zeer korte tijd zijn waar te nemen. Want om de tijdmeting op verschillende plaatsen passend te doen, en de lengte van nabije meridianen precies te vinden, wordt niet alleen vereist dat de tijd heel scherp wordt gemeten (dat is te doen), maar ook dat er geen merkbaar verschil is in de meting door twijfelachtigheid van de tekens. Zoals bijvoorbeeld: Als de tijd goed gemeten was met instrumenten, maar de meter twijdelde een minuut van een uur, of het teken voorbij was of niet, kon dit in het lengteverschil van de plaatsen 15 minuten van de evenaar scheelen, dat is meer dan twee 'dyitse mijlen' op onze parallel, bijna gelijk aan de afstand van Amsterdam tot Haarlem, wat in een kleine landstreek een groot verschil zou geven. Zo iets kan men door het gehoor niet verkrijgen, of tenminste niet overal. Want al zou in A, als daar middag gemeten werd, een kanon afgeschoten worden, dat men in B en C zou horen, toch zouden de meters |
|
in B en C als ze dit hoorden niet op hetzelfde ogenblik meten, maar lang daarna, omdat het geluid niet in een ogenblik, maar in een merkbaar verschillende tijd voortgaat. Bovendien zou het totaal ongeschikt zijn op meridianen ver van elkaar, daar het geluid van een kanon niet ver genoeg gaat. Laat staan de winden die het geluid helpen of belemmeren. En uit kleine afstanden van meridianen te besluiten tot een grote is geheel onzeker, maar als grote afstanden goed berekend zijn, kan men tussenliggende kleine makkelijker vaststellen. Als het oor ons niets te bieden heeft, zou men iets kunnen hopen van het oog. Want al gebeurt het gezicht op een punt van de tijd, ook van oneindig ver, toch kan de meter A aan de meter B alleen met vuur in de nacht, of met rook overdag een teken geven, en dat op zeer kleine afstand. Een licht kan men hoogstens 2 of 3 mijlen ver zien; en rook wordt gemakkelijk verspreid door de wind en heeft niet zo'n snelheid als het licht van vuur. Bovendien, om van A tot C een licht te kunnen laten schijnen, moeten de nevels in de lucht en de bultigheid van de aarde niet in de weg zitten, wat onmogelijk te verkrijgen is. Zodat men hierin van het oog ook niet veel kan verwachten, dan misschien op nabij gelegen plaatsen, waarbij de minste fout grote misslagen kan maken, en die kunnen ook niet de volmaaktheid van kaarten bevorderen, wat belangrijker is. Ook is nog op te merken dat, al zouden zulke beletselen niet voorvallen, het toch nodig zou zijn elkaar te waarschuwen op welke dag en welk uur men de tekens en de meting zou doen, wat niet altijd en overal gedaan zou kunnen worden, vanwege oorlog of anderszins. Nu het oog ons van nabij in de steek laat, en we toch geen nadere waarschuwing kunnen krijgen dan met geluid, moet men aan ander middel bedenken om een zeker teken van meten te geven.. Maar hiervoor is nodig dat niet alleen het teken wis en zeker is, en in korte tijd gebeurt, maar ook dat het gezien kan worden over zeer grote landstreken, ja zo goed als over een geheel halfrond van de aardbodem, om zowel tegelijk veraf gelegen plaatsen zoals A en C, als naburige, met B te kunnen vergelijken door gedane tijdmetingen. Dan moet er wel een teken zijn |
|
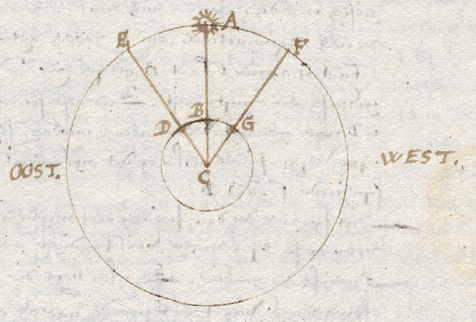
zeer ver van B, naar de hemel E, dat op alle gewesten naar A en C meteen is waar te nemen. Want hoe hoger een ding in de hemel staat, op hoe meer plaatsen op aarde het gezien wordt. Zo'n teken vinden we in de loop en het lichaam van de Maan, zoals wanneer deze haar licht komt te verliezen in de schaduw van de aarde, of te eclipseren. Wnat daarbij gelden zulke voorwaarden als de genoemde. Namelijk: 1. de hele wereld laten weten, en lange tijd van te voren voorspellen. 2. door de snelle loop van de maan is goed te onderscheiden wanneer de tekens te zien zijn en wanneer ze voorbij zijn. 3. de maan staat zo hoog dat ze op bijna van de helft van de aarde op eenzelfde ogenblik te zien is. Bovendien hebben we op de maan bij een Eclips verscheidene tekens, met als vier belangrijkste: 1. het begin van de eclips. 2. als de maan geheel de schaduw van de aarde ingaat, en haar licht helemaal verliest. 3. als ze haar licht weer begint te krijgen. 4. als ze weer geheel verlicht wordt en helemaal van de schaduw verlost is. Deze vier tekens geven het gemak dat, als er bij het ene teken iets hapert, door gissing of bij betrokken lucht, men toch de lengteverschillen kan weten door andere. Nu blijft over te bewijzen, hoe men hiermee een lengteverschil kan verkrijgen, wat we doen met de volgende figuur. Laat de Zon zijn P, in zijn eigen cirkel PMRP, de Maan S in haar cirkel, de Aarde VIO, met middelpunt A. Laat de maan beginnen te eclipseren als de zon in P is, tegenover de meridiaan AIL van de stad I, of in het onderste deel ervan onder de horizon, dan is het middernacht in I. Het is zeker dat de maan op hetzelfde ogenblik wordt gezien zowel oostelijk van I in V, als westelijk in O. Want de afstand van de maan S tot het middelpunt der aarde A, is ongeveer zestig keer zo groot als de halve diameter AI van de aarde. |
|
1. Ze gebeuren slechts om de vijf of zes maanden, en niet steeds op hetzelfde halfrond, zodat men niet elke dag of week kan meten, terwijl men het verschil van twee meridianen pas door 3 of 4 eclipsen met meer zekerheid kan onderzoeken. Ondertussen kunnen meters ziek worden of verhuizen, of anderszins verhinderd worden. 2. Niet alle meters zijn even bekwaam om de tekens van verduistering op de maan goed te onderscheiden, veel oefening is vereist; en mensen beoordelen verschillend wanneer de verduistering begint of eindigt. Weliswaar kan hiervoor de Hollandse verrekijker gebruikt worden, maar niet iedereen is eraan gewend, en het vereist niet minder oefening dan met het blote oog. 3. Maansverduisteringen zijn van die aard, dat ze de meter dikwijls enige tijd laten twijfelen of ze al begonnen zijn of niet, en wel om twee redenen: a. de duisternis op de maan begint niet plotseling, het juiste raakpunt van de schaduw is niet precies te onderscheiden, het kan wel 4 minuten duren. Te meer als de lucht wat dampig is en de maan bij de horizon staat. Want de dikte van de lucht maakt dan, dat de duisternis vroeger lijkt te komen dan het behoorde, en later weg te gaan, wat velen eerder heeft misleid. b. niet bij alle eclipsen gaat de maan precies midden door de schaduw van de aarde. Want als gesteld wordt dat de maan bij B in de schaduw komt |
| gaande naar C toe, dan kan men de snijding van de twee cirkels bij I terstond gewaarworden; |
| als de maan er zichtbaar is. Ook kan men weten hoeveel de maan voortgaat, elk uur en minuut van de dag. Dus kan ook een lengteverschil gevonden worden, zowel in F als in G en E. |
|
Want zoveel als de plaats van de maan gemeten in E, of G, op een zekere tijd verschilt van de plaats die de maan moest hebben in F, zoveel verschil E of G in lengte van F; wel te verstaan dat men het verschil tussen de gevonden en berekende plaats moet brengen tot uren en minuten van de maanloop, en dan tot graden en minuten op de evenaar. Dit zal beter te begrijpen zijn met een voorbeeld. Laat de maanloop berekend zijn op de meridiaan AFB, en in Ephemeriden (dagtafels) gebracht, om daaruit zijn plaats aan de hemel per uur en minuut te weten, en laat bevonden zijn dat de maan in 24 uur 13 graden loopt. Laat ook een meter in de stad E bevonden hebben dat de maan 's avonds om zes uur staat op 20 graden 30 minuten van het teken Kreeft. Maar als hij in de dagtafels ziet dat de maan is gesteld op 18 graden 30 minuten van Kreeft, zal hij besluiten dat E in lengte van F verschilt: 2 graden van de maanloop. Om de tijd te hebben zal hij zeggen: 13 graden geven 24 uur, wat geven 2 graden? Uitkomst: 3 uur 41 minuten, dat wil zeggen op de evenaar 55 graden 15 minuten*) voor het verschil tussen de meridianen AFB en AED. Om nu te weten te komen of E oostelijk of westelijk van F ligt, is te weten dat door meting de plaats van de maan in westelijke steden op hetzelfde tijdstip in de dagtafels altijd verder in de Dierenriem wordt gevonden; in oostelijke daarentegen niet zo ver. En dit is omdat de maan lopend van B naar D van oost naar west, eer ze van de meridiaan AFB komt op AED,
*) In 24 uur draait de aarde 360 graden, in 1 uur 15 graden; wat geeft 3 uur 41 minuten? Uitkomst 55 graden 15 minuten. |
|
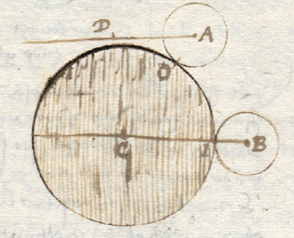
altijd nog oostelijker loopt, dan ze op zo'n tijdstip wordt gevonden in dagtafels die op AFB gemaakt zijn. Men kan ook de plaats van de maan opzoeken in de dagtafels, en zien welk uur daarbij past. Want dat uur zal altijd zoveel verschillen van het andere waarop de meting gebeurde, als het verschil van de meridianen vereist. Bijvoorbeeld: als de meter in E de maan vindt op 20 graden 30 minuten van Kreeft (zes uur 's avonds), en deze plaats opzoekt in dagtafels van F, zal hij vinden: 9 uur 41 minuten, en dus besluiten dat de meridiaan AED van AFB verschilt naar het westen 3 uur 41 minuten, zoals in de andere berekening. En deze manier is makkelijker dan de voorgaande. Anderen hebben getracht het lengteverschil te vinden uit de eclipsen van de Zon, eenzelfde teken nemend, zoals het begin of einde van de eclips, of een bepadld verduisterd gedeelte van het lichaam van de Zon. Want daar deze eclipsen in de ene stad ook op een ander uur gezien worden dan in de andere, en de loop van de Maan onder de Zon bekend is, volgt dat men uit de gemeten tijd en de loop van de maan (uit dagtafels berekend) het veschil van de meridianen van twee plaatsen ook passend kan vinden. Ook zijn er enigen geweest, die geprobeerd hebben in praktijk te brengen en af te stellen een Uurwerk dat eenparig gaat met de Zon, en dat in lange tijd helemaal niet aan ongelijkheiid of fout is onderworpen. Want als men zo'n uurwerk had, zou men het allermakkelijkst en allerzekerst het verschil der meridianen kunnen vinden op alle plaatsen van de wereld, op de volgende manier. Neem aan dat in deze figuur DGB de aardbol is, met middelpunt C, |
| de omtrek van de hemel EAF, drie steden in D, B en G, drie hemelmeridianen daarvan CE, CA, CF, met de andere overenkomende. Laat iemand in de stad B, |
|
midden op de dag, het uurwerk afstellen op de Zon, en af laten lopen. Het is onbetwijfelbaar, indien het uurwerk altijd eenparig ging zonder enige verandering, dat het niet alleen altijd middag zou wijzen als de Zon weer op de meridiaan in A kwam, maar ook alle uren daartussen, met hun minuten, correct zou afmeten en aanwijzen. Stel nu dat iemand zou reizen met het uurwerk, van stad B naar G of D, zonder dat er enige verandering of ontregeling in de gang van het uurwerk kon komen, dan zou het uurwerk altijd middag wijzen als de zon was gekomen in A. Want door het vervoer van het uurwerk van B naar G of D kon zijn loop niet veranderen. Als dan iemand in G, terwijl het uurwerk middag wees, de tijd aan de zon ging afmeten met een instrument, zou hij bevinden dat de zon niet stond op de meridiaan CGE, maar daar buiten in A, en dus een voormiddags uur hebben, omdat G westelijk van B ligt. En indien hij ging meten in D, zou hij een namiddags uur vinden, omdat D ten oosten van B ligt. Dit moet ook begrepen worden van alle andere uren en minuten van de dag, waarop men maar het uurwerk op de zon zou willen afstellen. Uit dit tijdverschil nu zou men het ware verschil van de meridianen op zekere wijze vinden. Want als de zon en het uurwerk altijd overeenkomen op de meridiaan CA, en het uurwerk werd op een andere meridiaan gebracht, zoals naar G, zou het zoveel moeten verlopen voordat de zon in F stond, als de boog AF uitmaakt op de dagelijkse omloop van de zon, gerekend op de evenaar. Dus als het middag was in G, zou terstond op het uurwerk zelf het tijdverschil gezien worden, dat men moest veranderen in graden en minuten op de evenaar, om het lengteverschil te hebben voor de stad G van de stad B, zoals hiervoor duidelijk genoeg is uitgelegd. En zo zou het ook toegaan als het uurwerk in D was gebracht. Want als het daar middag was, zou het een voormiddags uur aanwijzen, zoals het op da ogenblik in B zou worden bevonden. Dit zijn wel de drie voornaamste eerder bedachte middelen van lengtevinding, afgezien van maansverduisteringen. Nog één is er, gegrond op de magneetnaald en de afwijking ervan van het juiste noorden, die voor S. Stevin de aanleiding is geweest zijn Havenvinding te schrijven. Maar deze manier is zo vol |
|
2. Ten tweede is deze manier geheel onzeker omdat meting van plaatsen van de maan niet zonder fout kan gebeuren. De oorzaak is dat haar loop regelmatig wordt gemaakt ten opzichte van het middelpunt van de aarde, en niet ten opzichte van het oppervlak waar wij wonen. Hierdoor komt het dat de maan door verschillende mensen op het halfrond waar ze zichtbaar is, als ze gaan meten, op hetzelfde ogenblik op verschillende plaatsen van de hemel wordt gezien. Wat niet zou gebeuren als alle meters in het middelpunt van de aarde stonden. Ze zullen dus een verkeerde plaats vergelijken met de dagtafels, en zich grovelijk vergissen. Dit vereist enige verklaring, die we in de volgende figuur pogen te geven. |
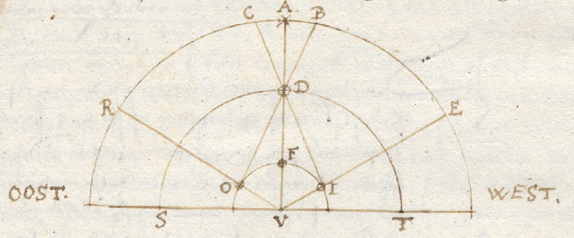
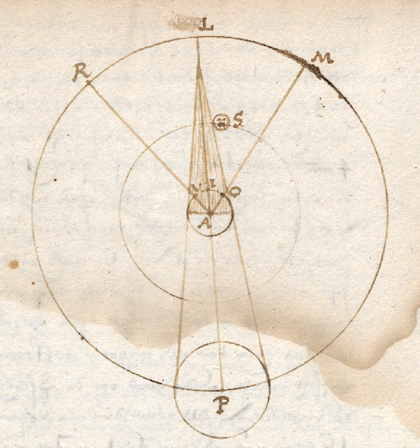
|
Laat de aarde zijn OFL, met middelpunt V, de cirkel van de maan SDT, de Dierenriem RAE, drie steden O, F, I, en de hemelmeridianen ervan VR, VA, VE. De dagtafels van de maanloop (gemaakt voor de stad F) worden zo gerekend alsof de maan vanuit V tegen de Dierenriem wordt gezien. Als nu op een zeker ogenblik de maan D vanuit F wordt gezien over de ster A op de meridiaan VDA, dan zou een meter in F de maan net zo zien als vanuit V. Maar een meter in de stad I zou de maan zien in C, ten oosten van de ster A. En een meter in de stad O zou haar zien in B zien, naar het westen. Dus vanuit I en O gezien wordt een andere plaats van de maan gezien dan A, zoals in de dagtafels staat, waardoor verkeerde lengteverschillen worden verkregen. Weliswaar kan men dit gezichtsverschil berekenen en in aanmerking nemen, |
|
maar het verandert zo veelvuldig en dikwijls zo vlug, ook zelfs terwijl men meet, dat het onmogelijk is alles zo te verhelpen dat men niet een fout maakt van graad of twee. Dit gezichtsverschil is ook afhankelijk.van de hoogte van de maan boven de horizon, wat blijkt uit deze figuur. |
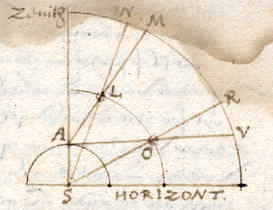
|
AO is de gezichtslijn van het oog in A op aarde, door de maan O tot in het punt V van de Dierenriem. Deze snijdt de lijn SO (die de ware plaats van de maan aanwijst) met een grotere hoek in O, dan de gezichtslijn AL (met de maan in L) de lijn SL snijdt in L. Dus R verschilt veel meer van V dan N van M. En dit is wat de metingen van de maan met intrumenten zo twijfelachtig en onbetrouwbaar maakt. Zodat ik durf te zeggen dat ware lengteverschillen er nooit mee gevonden zullen worden. Om deze twee genoemde redenen is lengtevinding met de loop en plaats van de Maan geheel onzeker. De tweede manier, met eclipsen van de Zon, zou daartoe wel de beste grondslag geven, als er niet veel aanleidingen waren om te missen: 1. Tegen de zon gezien is de maan aan dezelfde gezichtsverschillen onderworpen als nu besproken zijn. Waardoor begin en eind van de eclipsen niet op dezelfde tijd komt voor alle mensen die Oost en west wonen, zoals bij de eclipsen van de maan; en ook dat de zichtbare loop van de maan over de zon niet op alle plaatsen even snel of langzaam gaat, terwijl daaruit het verschil der meridianeen zou moeten blijken, om de ermee evenredige tijd goed te vinden. 2. Eclipsen van de zon komen nog minder vaak voor dan die van de maan,. 3. Voor zeer precies waarnemen ervan zijn weinig hemelmeters genoeg geoefend. |
|
Het is wel waar dat goede waarnemingen van een zon-eclips, op verschillende plaatsen, gebruikt kunnen worden om iets op te bouwen. Men meet die met een passer op een bord, door een hollandse verrekijker ingelaten in een donkere ruimte op een vlak bord*). Waarbij Eclipsen van de maan, waargenomen met het blote oog, het niet kunnen halen.
*) Zie de uitvoerige beschrijving van de waarneming van de zonsverduistering van 10 juni 1630 in het 'Journal' van Isack Beeckman, T. 3, p. 152-157. Hortensius was daarbij aanwezig. Dit zou het gemakkelijkst zijn en het zekerst. maar het heeft de meeste onvolmaaktheden. Uurwerken worden gemaakt van harde stof of van een vloeiende stof. Die van harde stof moeten lopen over raderen, door gewicht of door veren. De raderen, van koper of ijzer, heeft niemand ooit zo goed kunnen vijlen dat de tandjes precies even ver van elkaar blijven, en dit zal ook nooit gedaan worden. Bovendien verslijten ze. Het gewicht blijft niet gelijk, omdat het aan touwen moet hangen. De veren persen niet altijd gelijk, afhankelijk van de uitrekking. Ook hebben veren, snaren en raderen te iijden van de verandering van de lucht, in krimpen en rekken. Die van een vloeiende stof zijn zandlopers of waterlopers. Ze staan in de lucht en sluiten die ook in, ze hebben dus last van hitte of koude of andere veranderingen van de elementen. Kortom, nog niemand heeft een eenparig lopend uurwerk in praktijk gebracht dat zonder schade of ontregeling kon worden vervoerd. |
|
De edele heer Galilei heeft een ander middel gevonden en aan de Hoogmogende Heren aangeboden om in het werk gesteld te worden, tot nut van het menselijk geslacht en in het bijzonder van ons lieve vaderland. Te weten is dat omtrent 30 jaar geleden door Jacob Metius van Alkmaar onze verziende brillen aan de dag zijn gebracht, en door de heer Galilei nagemaakt en gebruikt bij het onderzoek van de hemellichamen. Hij ontdekte bij de planeet Jupiter vier andere kleine planeetjes, die aan alle Oude Filosofen nooit bekend zijn geweest. Met Jupiter worden ze in 12 jaar rond de Dierenriem gedragen. Hij noemde ze de Sidera Medicaea, ter ere van het huis der Medici en speurde van jaar tot jaar hun loop na. Hij vond opmerkenswaardige dingen: 1. Het lichaam van Jupiter is donker zoals de aarde, het wordt door de zon verlicht en maakt een schaduw achter zich, zoals de aarde. 2. De planeetjes van Jupiter worden in die schaduw wel eens verduisterd en verliezen dan hun licht dat ze van de zon ontvangen (de gemeenschappelijke fontein van licht in de planetenwereld). 3. Ze ontmoeten elkaar dikwijls en scheiden zich dan weer af van elkaar. 4. Dikwijls schuilen ze voor of achter het lichaam van Jupiter en dan worden ze onzichtbaar. Uit deze en dergelijke gebeurtenissen heeft Galilei een betrouwbaar en geschikt middel gevonden |
| om lengteverschillen zeer precies te onderscheiden, dat we nu zullen behandelen aan de hand van figuren. |
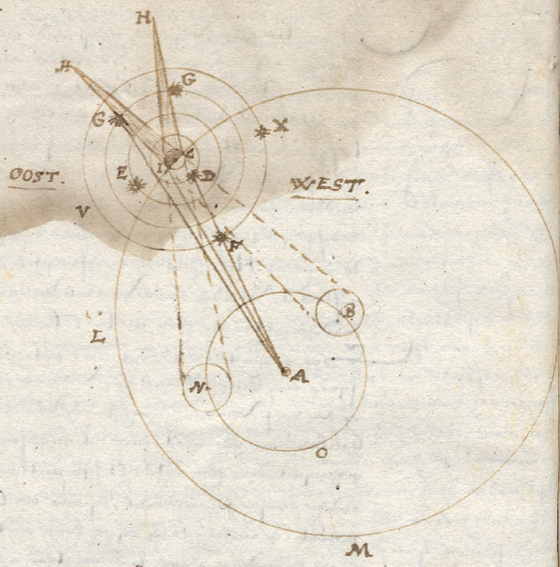
|
A is de aarde met ons oog, de zon staat in B, en loopt in de cirkel BNO, Jupiter staat in C, en zijn cirkel die hij in 12 jaar doorloopt is CLM. Het lichaam van Jupiter wordt alleen verlicht aan de kant van de zon en er moet een schaduw CHI achter zijn ten westen, die tot in H steeds dunner wordt, omdat de zon groter is dan Jupiter. De vier planeetjes zijn D, E, F en G, en draaien elk in een eigen cirkel rond Jupiter van west naar oost: 1. Ze staan soms boven Jupiter in H, soms eronder in F, dat is voor ons gezicht soms achter Jupiter en soms ervoor. 2. Ze zijn nu eens oostelijk van Jupiter, dan weer westelijk. 3. Van H naar V lopen ze een stuk naar het oosten en bij V schijnen ze stil te staan, dan keren ze naar het westen totdat ze bij X weer stilstaan, en daarna gaan ze weer naar Jupiter toe. 4. Soms schijnen ze in de schaduw van Jupiter te gaan, soms er uit te komen. 5. Ze schijnen nu eens elkaar, dan weer het lichaam van Jupiter, te raken en weer gecheiden te worden. |
| Om te begrijpen hoe het toegaat voor ons gezicht, moet men de volgende figuur bekijken. |

|
Zo ongeveer vertoont Jupiter zich, gezien door de verrekijker, met de planeetjes nu eens oostelijk, dan weer westelijk ervan, altijd bijna op een rechte lijn. Ze gaan van A en O naar het Oosten, verbergen zich achter Jupiter en komen bij D weer te voorschijn. Soms komen ze van C naar E naar het westen, en dan gaan ze voorbij D onder Jupiter, alsof ze er weer achter schuilden. We kunnen niet zien hoe hoog of laag ze zijn, maar soms valt de schaduw van Jupiter op een planeetje uit A, voor- of nadat het de schijf raakt. Zie de voorgaande figuur bij G (planeetje gaat naar het oosten): de gezichslijn AG ligt links van AI. Het tegendeel gebeurt als de zon in N staat. De planeetjes ontmoeten elkaar ook, zoals C en B, rakend of zeer nabij. Zie ook in de eerste figuur D en F, op één gezichtslijn. Om nu te begrijpen waarin het voorstel van Galilei eigenlijk bestaat, is te weten dat hij de loop van de planeetjes langdurig heeft waargenomen, en in rekentafels gesteld. |
|
Hij wil dat elke meter met een goede verrekijker ernaar kijkt, en de tijd precies meet. Want uit wat gezegd is volgt, dat het tijdverschil het verschil van meridianen passend kan aanwijzen. Daar iemand kan twijfelen of aan alle genoemde voorwaarden voldaan wordt, zowel bij de tekens als bij de meters, zullen we hierna bekijken de volmaaktheden die er volgens Galilei zijn in deze manier van lengtevinding. Eerst geven we van de planeetjes de volgorde, grootte en tijd van elks omloop om Jupiter, aan de hand van de volgende figuur. |
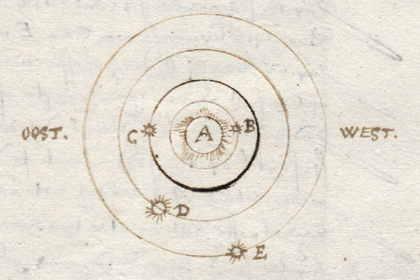
|
A is het lichaam van Jupiter, met er omheen vier cirkels van de vier Mediceïsche sterren. B is het dichtst bij Jupiter, het kleinst en het snelst: omloopstijd 42 uur. De tweede, C, is trager: omloopstijd Daarna komt in grootte de vierde, E, de traagste: omloopstijd 17 dagen. De derde, D, is het grootst, omlooptijd 7 dagen. Deze omloopstijden heeft Galilei lang geleden zo vastgesteld, in zijn boek over de gestalte des werelds*). Maar ongewijfeld heeft hij ze voor dit werk van de
*) Dialogo, 1632, p. 112; Engl. 1661, p. 101; Ned.: Hans van den Berg, Amst. 2012, p. 185. |
|
lengtevinding al onderzocht tot uren en minuten toe. Laot ons nu zien welk voordeel in deze manier boven alle andere door hem is bespeurd. Voorwaarden waaraan voldaan moet worden door de tekens: 1. Ze moeten zeer dikwijls gebeuren. 2. Zo hoog zijn, dat ze op een halfrond van de aarde te zien zijn. 3. Wis en zeker zijn, en in zo korte tijd dat ze geen twijfel laten aan het oordeel van de meter. 4. Enige tijd van te voren te voorspellen. 5. Zich op hetzelfde ogenblik gelijk vertonen aan alle mensen die ze zien. Voorwaarden voor de meters: 1. Ervaren in het afgissen van de tekens. 2. Het moeten er veel zijn. 3. De tijd goed kunnen meten, met goede instrumenten. Alle voorwaarden zijn te vinden in de uitvinding van Galilei: 1. Door de snelle omloop van de planeetjes B en C zijn in een etmael dikwijls een of twee teken te zien, als Jupiter niet te dicht bij de zon staat (bij ons hoogsten 2 maanden per jaar, in de hete landen nauwelijks 1 maand). 2. Jupiter is te zien op een halfrond van de aarde. 3. Wis en zeker zijn: de ontmoeting, indompeling in de schaduw en uittrede, verberging achter Jupiter, en er weer uitkomen. |
| De laatste op zichzelf, en ook in het oog van de meter, als hij maar een goede verrekijker heeft. Galilei heeft zulke goede verrekijkers gebruikt dat ze Jupiter geheel naakt en passer-rond vertonen, en zeer groot, ja 3 of 4 maal zo groot als in de beste Hollandse 'brillen'. |

|
Wij zien Jupiter ruig zoals in de eerste figuur, hij ziet hem zoals in de tweede figuur. Wij zien Jupiter en een planeetje niet dichter bij elkaar dan in de eerste figuur, zoals ik menigmaal heb onderzocht, hij ziet een raking zoals in de tweede figuur. Wat de tijd betreft: het ingaan in de schaduw, of achter Jupiter, duurt hoogstens een minuut, Bij de ontmoetingen heeft hij gezien dat de meter soms maar 10 of 12 seconden in twijfel is. Dit is van uitnemend belang voor meridianen dicht bij elkaar: een halve minuut in de tijd betekent 7½ minuut op de evenaar [14 km]. 4. Galilei heeft de loop van deze planeten zo nauwkeurig onderzocht, dat hij |
|
deze tekens ettelijke maanden van te voren kan voorspellen, en in dagtafels zetten. 5. Deze tekens worden overal op hetzelfde ogenblik op gelijke wijze gezien. Jupiter staat zo hoog, dat het niet uitmaakt of we de tekens zien vanuit het middelpunt van de aarde of vanaf het oppervlak. Tot zover de tekens. Wat de meters betreft, kan het de uitvinding ook niet aan volmaaktheid schorten: 1. Men kan iemand in 2 a 3 weken geheel bekwaam maken om de tekens goed af te gissen, omdat ze zo snel voorbij zijn en zo dikwijls terugkomen. Bij maansverduisteringen is 6 a 7 jaar ervaring nodig. 2. Met veel verrekijkers kan men veel mensen op veel plaatsen van de wereld tegelijk hierin oefenen. 3. Iemand kan in een week de tijd leren meten met geschikte instrumenten, daarvoor is slechts nodig kennis van de sterren en van de Globe. Doch in dit geval heeft Galilei iets in praktijk gebracht om de tijd zeer scherp te meten, als met een klok, wat hij later bekend zal maken. Uit dit alles volgt dat deze manier niet alleen de beste, maar ook de enige is, om te komen tot ware kennis van lengteverschillen, in korte tijd. Ze is niet heel ingewikkeld in rekenen of meten, en er zijn geen dure instrumenten voor nodig. Alleen een goede verrekijker en een simpel gezicht om de tekens af te gissen, met een geschikt instrument om de tijd te berekenen of aan de sterren te meten. Iedereen met verstand kan niet anders oordelen dan dat deze manier van lengtevinding het waard is, door de Hoogmogende Heren genereus te worden aangenomen, opgekweekt en tot volmaaktheid gebracht. |
|
1. Alle landkaarten zullen gezuiverd kunnen worden van grove fouten in de lengte van steden en kleinere gebieden. Dat is een van de profijtelijkste dingen die aan het menselijke geslacht meegedeeld kunnen worden. 2. Op zee zullen alle havens en eilanden op de juiste plaats op de kaart kunnen liggen. Stuurlieden zullen beter weten of een verkeerde gissing komt door eigen fout of door verborgen stromen. Menig gevaar van schipbreuk zal voorkomen worden. 3. Het grootste nut zal komen indien verrekijkers op zee goed gebruikt kunnen worden. Dan kan men altijd onderzoeken op welke lengte men is met het schip, en bijeenkomsten van vloten op zee houden. Hoe groot het profijt is dat dit geven zal aan de scheepvaart van deze landen, kan iedereen bedenken. De vorderingen van de laatste jaren zullen worden overtroffen als men de zaak op last van de Hoogmogende Heren ten einde kan brengen zoals gezegd is. Ik laat nu staan de reputatie die deze stad bij alle buitenlandse naties zal krijgen, |
|
als ze zullen zien dat er niets overblijft dat nog niet bezocht of bevaren is, dat het vernuft van alle wetenschappen hier te lande in het werk wordt gesteld, zodat we de hele wereld aan ons proberen te verplichten met de nuttige uitwerking van mooie uitvindingen. En tenslotte dat de Hoogmogende Heren voor de juiste Maecenas van alle goede verstanden moeten worden gehouden, en voor de kloekste uitvoerders van de allerloffelijkste der moeiten. Dit zij voor deze keer genoeg over de vinding van het ware Oost en West, waarnaar eerder door velen naarstig is gezocht, maar die door niemand zo goed is benaderd als door de Edele Heer Galilei.
|