Was dat niet toevallig, met die getallen 4 en 2?
2e Voorbeeld (1e vorm):
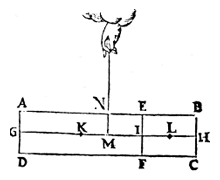Gegeven een andere balk, verdeeld in een groot en een klein stuk. K en L zijn de zwaartepunten.
Te bewijzen (zonder getallen): gewicht omgekeerd evenredig met arm.
Maer op datmen niet en dencke dit daer also by ghevalle ghesciedt te sijne, wy sullender Wisconstich bewys af doen aldus:
T G H E G H E V E N. Laet ABCD wederom een pilaer sijn [...], ende het swaerheyts middelpunt van het deel EFDA sy K, int middel van GI, ende van het deel EFCB, sy L int middel van IH, ende des heels ABCD sy M int middel van GH, ende MN sal der deelen EFDA ende EFCB handthaef sijn, daer an sy evestaltwichtich hanghen.
T B E G H E E R D E. Wy moeten bewysen dat ghelijck het lichaem ofte de swaerheydt (twelck hier een selfde is [...], overmits den pilaer door tghestelde overal eenvaerdigher swaerheyt is) van EFDA, tot EFCB, alsoo den langsten erm ML, tot den cortsten MK.