Home | Chr. Huygens | < Oeuvres XII

Voorwoord, Theor. I ... IX, Prop. X, XI, XII, Theor. X ... XVI, Prop. XX
Probl. I ... VIII

[ 113 ]

Christiaan Huygens, Const.z.

Vondsten

over de

Grootte van de cirkel

Waarna volgen

Constructies van enige beroemde problemen.

Leiden, Bij Johannes & Daniel Elzevier.
Acad. Drukkers

M DC LIV..

[ 115 ]

[ 1654 ]

Voorwoord.

Ten aanzien van het oude probleem van het Tetragonisme*), dat bij degenen die niets van Wiskunde weten wel het meest bekende is, hebben wij onlangs iets verricht dat de moeite waard is, naar wordt gemeend, en enige dingen verkregen die volgens ons beter zijn dan wat tot nu toe is doorgrond; de bewijzen willen wij aan de Meetkundigen meedelen. Want we denken dat ze zowel voor hun studie van nut zullen zijn, als door de nieuwheid zelf een prikkel tot het zoeken naar verborgen zaken, voor hen die bedenken dat ook bij dit onderwerp — waarmee allen zich lang geleden met de grootste inspanning hebben beziggehouden — het een en ander is overgebleven dat aandacht verdient.
Wel hebben velen eerder getracht zich de roem voor het vinden van de Kwadratuur toe te eigenen, en herhaaldelijk verschillende gedachtenspinsels openbaar gemaakt, ware met onware vermengend. Maar we weten dat ze alle door kundiger mensen ofwel zijn neergehaald, of gering geschat, en er is nog niets anders aanvaard, waarop elke afmeting van de cirkel kon steunen, dan dit ene: dat deze groter is dan een ingeschreven veelhoek en kleiner dan een omgeschreven veelhoek.
Doch wij verschaffen nu een nadere bepaling en tonen aan: bij twee veelhoeken die middelevenredig zijn tussen een ingeschreven en een omgeschreven veelhoek, daarmee gelijkvormig, is de omtrek van de kleinste ervan groter dan de cirkelomtrek, en de andere veelhoek overtreft de oppervlakte van de cirkel in dezelfde verhouding¹). En terwijl dit wel onder wat we zullen bewijzen zowel het moeilijkste lijkt, als in het bijzonder aanmerkenswaardig, zijn er toch andere die niet alleen nauwkeuriger zijn²), maar die ook meer van nut zullen blijken; deze zullen we echter niet hier vooraf opsommen, als zijnde beter te begrijpen in het volgende.
Het zal evenwel goed zijn kort uiteen te zetten wat ze bijdragen aan de studie van de Meetkunde, aangezien ze in niet geringe mate zijn aan te bevelen om hun bruikbaarheid. Nu hebben we van het voorgestelde een dubbele behandeling ingericht, door eerst datgene te leveren waarvan het bewijs berust op de gewone beginselen van de Meetkunde, en vervolgens ook een beschouwing van zwaartepunten toe te passen;

[ *) Grieks voor vierhoekig maken, 'vierkanting' of kwadratuur.
NB: De noten zijn meestal sterk bekort; soms is er een toegevoegd.
De marge-noten in de brontekst van 1654 zijn {tussen accoladen} in de tekst opgenomen.]
¹) Zie Theor. XI, Prop. XIV op p. 151. [...] De gelijke verhouding staat aan het eind, op p. 155.
²) Vergelijk de noten 13 en 17 op p. 96 en 97.

[ 117 ]

bij het eerste zal men inderdaad uitgelegd vinden, hoe niet alleen bij de omtrek van de hele cirkel³), maar ook bij een willekeurige gegeven boog⁴) een rechte lijn is te vinden die er aan gelijk is; op een manier die geschikt is voor Mechanische constructies, en die zelfs de subtielste daarvan het minst zal verijdelen. Evenzo hoe door hen die met getallen bezig zijn de verhouding van de omtrek tot de middellijn, die Archimedes haalde uit veelhoeken met 96 zijden, met alleen twaalfhoeken kan worden bevestigd⁵). En uit veelhoeken met 10800 zijden: terwijl er voor degenen die de oude weg bewandelen nog maar deze grenzen van de omtrek bestaan, 62831852 en 62831855, bij een diameter van 20000000 delen, zal gezien worden dat die met onze Methode zijn verlegd naar 6283185307179584 en 6283185307179589⁶); en dat steeds het dubbele aantal ware cijfers wordt verkregen, hoe groot ook het aantal zijden is van de veelhoeken die gebruikt worden. Dat het inderdaad om een bepaalde reden⁷) gebeurt hebben we ingezien, zoals ook een kwadraat van een willekeurig getal meestal wordt opgesteld met tweemaal zoveel cijfers als het getal zelf.
Maar nog meer bekorting verschaft een eigenschap van zwaartepunten, en hierdoor schijnen we enigszins dichterbij de volmaking van dit onoverwinnelijke probleem te zijn gekomen. In elk geval hebben we nu voor het vaststellen van de Archimedische grenzen van de omtrek alleen nodig dat de zijde van de ingeschreven driehoek bekend is⁸). En met een zestighoek bewijzen we⁹) dat deze begrensd is tussen 31415926538 en 31415926533, als de middellijn wordt gesteld op 10000000000, terwijl met de gebruikelijke methode nog maar te voorschijn worden gebracht 3145 en 3140. Zodat het aantal ware tekens hier al het drievoudige is en meer, zoals met het voorgaande het dubbele; en inderdaad met voortdurend succes, evenals bij grotere getallen wordt opgemerkt dat de derde macht het drievoudige heeft van het getal zelf⁷). Dus als men voortaan de grootte van de omtrek onjuist bepaalt, zal men niet weerlegd worden met veelhoeken die talloze zijden hebben, maar met een korte en geenszins ingewikkelde berekening, en beweren dat deze fout is, wat tot nu toe bijna een gewoonte is, zal men niet gemakkelijk kunnen.
Bovendien, als er iets is in de Tabel van de koorden, en iedereen weet van hoeveel belang het is dat deze wordt gecorrigeerd, als er bij het samenstellen ervan een fout is begaan of van elders iets verkeerds is binnengeslopen, zal het niet moeilijk zijn dit met behulp hiervan te herstellen, daar nu op een andere manier uit de in de cirkel ingeschreven veelhoeken de lengte van de bogen gevonden kan worden waarover de koorden zich uitstrekken. Ja zelfs ook voor wie van alle hulp van Tabellen verstoken is laten we zien, hoe zij uit de gegeven zijden van driehoeken de hoeken ervan kunnen opsporen¹⁰), zodat er nooit een afwijking van twee seconden van de ware is, en dikwijls zelfs geen zestigste deel van een seconde. En we vertrouwen erop dat deze dingen inderdaad beschouwd zullen worden als van niet gering belang. En we hebben vernomen dat ook René

³) Zie Probl. II, Prop. XI op p. 143. ⁴) Zie Probl. III, Prop. XII op p. 147.
⁵) Vgl. Probl. I, Prop. X op p. 139. ⁶) Vgl. het eind (p. 143) van Prop. X.
⁷) Zie noot 15, p. 142. ⁸) Vgl. p. 173-177. ⁹) Vgl. p. 179.
¹⁰) [...] Zie p. 179, laatste alinea [sinustabel genoemd op p. 181]. De hoogte van de driehoek geeft de koorde behorende bij het dubbele van een hoek, en zo de boog. Zie ook p. 163, met verwijzing naar Snellius.

[ 119 ]

Descartes, door wiens vondsten zowel de gehele Filosofie als de Wiskunde zeer is verlicht, hierover het een en ander op papier heeft gezet¹¹). Men zegt dat dit na zijn dood in aantekeningen is gevonden, en tot nu toe hebben we niet te weten kunnen komen met welke ijver of met welk resultaat hij hieraan de hand heeft geslagen. Doch van de geleerde meetkundige Willebrord Snellius bestaat Cyclometricus¹²), met veel arbeid geschreven, dat helemaal hierover gaat. En hij zou niet weinig lof hebben verdiend, als hij de twee voornaamste theorema's, waarop heel dit werk als op fundamenten is opgetrokken, had kunnen bewijzen¹³). Maar wat hij daar verlangt als bewijs te worden aangenomen, bevestigt het voorgestelde geenszins; deze theorema's bevatten echter een opmerkelijke waarheid, zoals we voor elk met een duidelijke redenering aantonen. En we hebben gemeend deze inderdaad met recht in het volgende op te moeten nemen, omdat hun oorzaken berusten op onze vondsten.

¹¹) Uit brief No. 5323 (31 dec. 1653) van Const. Huygens blijkt dat Chanut de papieren van Descartes wilde doornemen met zoon Christiaan, om te zien of er nog iets publiceerbaar was over filosofie of wiskunde. [...] Het schijnt dat de laatste de papieren niet heeft gezien, maar wel de inventaris, die zijn vader had. [...] Inderdaad verscheen later R. Des-Cartes Opuscula posthuma, physica & mathematica (Amst. 1701) met 'Excerpta', waarin iets over de lengte van koorden en hun bogen, en 'Ad quadrandum Circulum'. [...]
¹²) Zie over Snellius en het aangehaalde werk [1621] p. 94, n. 5 en 6.
¹³) Zie over deze theorema's p. 95, n. 8 en p. 157 en 159.

[ 121 ] [ 1654 ]

Christiaan Huygens, Const.z.

Vondsten

over de

Grootte van de cirkel.

Theorema I. Propositie I.
Als bij een segment van een Cirkel, kleiner dan de halve cirkel¹), de grootste driehoek wordt ingeschreven, en als bij de overgebleven segmenten evenzo driehoeken worden ingeschreven, zal de eerst beschreven driehoek kleiner zijn dan het viervoudige van de twee samen die in de overgebleven segmenten zijn beschreven.

Laat er een cirkelsegment ABC zijn, kleiner dan de halve cirkel¹), waarvan de middellijn BD is; en de grootste ingeschreven driehoek is ABC, dat wil zeggen dat hij de basis en de hoogte gelijk heeft met het segment. En bij de twee overgebleven segmenten worden ingeschreven de evenzo grootste driehoeken AEB en BFC.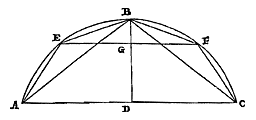
Ik zeg dat driehoek ABC kleiner is dan het viervoudige van de driehoeken AEB en BFC samen genomen.
Immers: laat verbonden worden EF, die de middellijn van het segment snijdt in G. Aangezien nu boog AB in tweeën wordt gedeeld in het punt E, zal elk van beide delen EA en EB groter zijn dan de helft van AB. En daarom zal het kwadraat van AB kleiner zijn dan het viervoudige van het kwadraat van EB of EA. En zoals het kwadraat van AB tot het kwadraat van EB, zo is DB tot BG in lengte; omdat namelijk het kwadraat van AB gelijk is aan de rechthoek die wordt omvat door DB en de middellijn van de hele cirkel*), en het kwadraat van EB gelijk aan de rechthoek onder dezelfde middellijn en de rechte BG. Dus is BD kleiner dan het viervoudige van BG. Maar ook is AC kleiner dan het dubbele van EF, aangezien AB aan deze gelijk is. Dus blijkt driehoek ABC kleiner te zijn dan het achtvoudige van driehoek EBF. En aan deze driehoek zijn gelijk AEB en BFC afzonderlijk. Dus zal driehoek ABC kleiner zijn dan het viervoudige van deze samen. Wat aangetoond moest worden.

¹) Zie de 'Errata', p. 215. Maar de beperking is niet noodzakelijk.
[ *) Teken de hele cirkel, middellijn BDP en AP; dan is DB : AB = AB : BP , dus AB² = DB × BP . 'Rechthoek' staat voor 'product', en 'kwadraat' is ook 'vierkant'.]

[ 123 ]

Theor. II. Prop. II.
Als er een cirkelsegment is, kleiner dan de halve cirkel, en op dezelfde basis een driehoek, waarvan de zijden raken aan het segment; en er wordt een lijn getrokken die het segment raakt in de top: dan zal deze van de genoemde driehoek een driehoek afsnijden die groter is dan de helft van de grootste driehoek binnen het segment beschreven.

Laat er een cirkelsegment ABC zijn, kleiner dan de halve cirkel, met B als top. En laat aan het segment raken aan de einden de rechten AE en CE, die samenkomen in E; ze komen immers samen omdat het segment kleiner is dan de halve cirkel. Verder wordt getrokken FG, die dit raakt in de top B; en getrokken worden AB en BC.
Aangetoond moet dus worden, dat de driehoek FEG groter is dan de helft van de driehoek ABC.
Het staat vast dat de driehoeken AEC en FEG, en evenzo AFB en BGC, gelijkbenig zijn, en dat FG doormidden wordt gedeeld in B. En FE en EG zijn beide samen groter dan FG; dus is EF groter dan FB, of FA. De hele AE is dan kleiner dan tweemaal FE. En daarom zal driehoek FEG groter zijn dan een vierde deel van driehoek AEC. Zoals nu FA tot AE is, zo is de hoogte van driehoek ABC tot de hoogte van driehoek AEC, en de basis is voor beide dezelfde AC. Dus, daar FA kleiner is dan de helft van de hele AE, zal driehoek ABC kleiner zijn dan de helft van driehoek AEC. Maar groter dan het vierde deel hiervan was driehoek FEG. Dus is driehoek FEG groter dan de helft van driehoek ABC. Wat aangetoond moest worden.

Theor. III. Prop. III.
Elk cirkelsegment kleiner dan de halve cirkel¹), heeft tot de grootste ingeschreven driehoek een verhouding groter dan vierderde.

Laat er een cirkelsegment zijn, kleiner dan de halve cirkel¹), waarin de grootste driehoek ABC is ingeschreven. Ik zeg dat het segment tot de genoemde driehoek een verhouding heeft die groter is dan van vier tot drie.
Laat namelijk ook in de overige twee segmenten de grootste driehoeken ADB en BEC zijn ingeschreven. Dus is driehoek ABC kleiner dan het viervoudige van deze samen {* volgens 1. hier}; en derhalve kan een of ander oppervlak aan driehoek ABC worden toegevoegd, dat samen daarmee ook kleiner is dan het viervoudige van de genoemde driehoeken ADB en BEC samen.

[ 125 ]

Laat daarom dus de driehoek AFC erbij worden gedaan, zodat het hele oppervlak ABCF kleiner is dan het viervoudige van de driehoeken ADB en BEC. En verder stellen we ons voor dat in de overige segmenten de grootste driehoeken worden ingeschreven; en evenzo steeds in de overige, totdat de segmenten waarin het laatst wordt ingeschreven samen kleiner zijn dan driehoek ACF, want dit kan gedaan worden²). 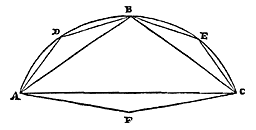Dus zullen ook de laatst ingeschreven driehoeken samen kleiner zijn dan driehoek ACF.
Omdat nu de twee driehoeken ADB en BEC samen groter zijn dan een vierde deel van het oppervlak ABCF. En omdat weer groter dan een vierde deel van deze twee, de vier driehoeken zijn die in de overige segmenten worden ingeschreven. En groter dan een vierde van deze evenzo de volgende; en zo steeds verder, als er meer beschreven zijn. Daarom zal het oppervlak samengesteld uit de vierhoek ABCF en de overige ingeschreven driehoeken, en een derde van die, welke het laatst zijn ingeschreven, groter zijn dan vierderde van de vierhoek ABCF zelf. Door Archimedes is immers bewezen³), dat als er een aantal oppervlakken is in viervoudige verhouding, deze alle samen met een derde van het kleinste, een verhouding van vierderde hebben tot het grootste.
Dus door te verdelen zullen alle driehoeken beschreven binnen de segmenten ADB en BEC met een derde van de laatst beschrevene, groter zijn aan een derde deel van het oppervlak ABCF. Maar het eerder genoemde derde is kleiner dan een derde van driehoek ACF. Dus als daarvan wordt afgenomen het derde van de laatst ingeschrevene, en van oppervlak ABCF wordt weggenomen de driehoek AFC, zullen alle driehoeken binnen de segmenten ADB en BEC beschreven, groter zijn dan een derde van driehoek ABC {* 33.5 Elem.⁴)}. En door samenstellen zal daarom de hele rechtlijnige figuur die in segment ABC is ingeschreven groter zijn dan vierderde van driehoek ABC, en des te meer het segment zelf. Wat te bewijzen was.

²) Zie het bewijs van Prop. 2 van boek 12 van de Elementen van Euclides.
³) Prop. 23 van 'Kwadratuur van de parabool': "Als een aantal grootheden achtereenvolgens in viervoudige verhouding wordt opgesteld, zijn al deze grootheden, samen met een derde deel van de kleinste ervan, in grootte gelijk aan vierderde van het grootste", p. 154 in ed. Basel 1544. [Engl.]
⁴) "Als er een grotere verhouding is van geheel tot geheel, dan van afgenomene tot afgenomene, zal er ook van de rest tot de rest een grotere verhouding zijn dan van geheel tot geheel". Zie p. 526 van de Euclidis Elementorum libri XV, ed. Clavius, 1607.

[ 127 ]

Theor. IV. Prop. IV.
Elk cirkelsegment kleiner dan de halve cirkel, is kleiner dan tweederde van de driehoek die dezelfde basis heeft, en zijden die aan het segment raken.

Laat er een cirkelsegment ABC zijn, kleiner dan de halve cirkel, en laat aan de uiteinden van de basis daaraan raken de rechten AD en CD, die samenkomen in het punt D. Ik zeg dat Segment ABC kleiner is dan tweederde van driehoek ADC.
Immers, laat getrokken worden EF die het segment raakt in de top B, en de grootste ingeschreven cirkel ABC. Daar dus de driehoek EDF groter is dan de helft van de driehoek ABC {* volgens 2. hier}, is duidelijk dat van de eerste een gedeelte kan worden afgesneden. zodanig dat de rest toch nog groter is dan de helft van de genoemde driehoek ABC. Laat dus op deze wijze afgesneden worden de driehoek EDG. En verder worden getrokken de rechten HI en KL, die de overblijvende segmenten AMB en BNC raken in hun toppen, en daarin de grootste ingeschreven driehoeken. En we stellen ons voor dat hetzelfde gedaan wordt met de overige segmenten, totdat tenslotte de overblijvende segmenten samen kleiner zijn dan het dubbele van driehoek EDG. Dan zal bij het segment een of andere rechtlijnige figuur zijn ingeschreven, en een andere omgeschreven.
En aangezien driehoek EGF groter is dan de helft van driehoek ABC; en weer de driehoeken HEI en KFL groter dan de helften van de driehoeken AMB en BNC; en aangezien dit steeds met dezelfde verhouding bij de overige plaats vindt, zodat de driehoeken boven de toppen van de segmenten opgericht, groter zijn dan de helft van die welke binnen die segmenten zijn beschreven; daarom blijkt dat alle driehoeken buiten het segment geplaatst ook zonder driehoek EGD samen groter zijn dan de helften van alle driehoeken binnen het segment beschreven. Maar nu is ook driehoek EGD groter dan de overige segmenten in het segment. Dus zal driehoek EDF samen met de overige driehoeken die buiten het segment zijn, groter zijn dan de helft van het hele segment ABC. En daarom zal des te meer het oppervlak omvat door de rechten AD en DC en de boog ABC, groter zijn dan de helft van segment ABC. En derhalve driehoek ADC groter dan anderhalf maal het segment ABC. Wat te bewijzen was.

[ 129 ]

Theor. V. Prop. V.
Elke cirkel is groter dan een veelhoek met gelijke zijden daarin ingeschreven en het derde deel van het overschot waarmee deze veelhoek een andere ingeschreven veelhoek met de helft van het aantal zijden te boven gaat.⁵)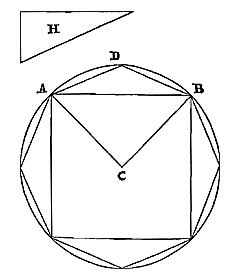

Laat er een cirkel zijn met middelpunt C; en laat er een veelhoek worden ingeschreven met gelijke zijden, waarvan AB er een is. En laat evenzo een andere veelhoek worden ingeschreven, waarvan twee zijden AD en DB worden onderspannen door AB. Deze is dus groter dan de eerste veelhoek. Laat nu het oppervlak H gelijk zijn aan een derde deel van het overschot. Ik zeg dat de cirkel groter is dan veelhoek ADB samen met het oppervlak H.
Immers: laat vanuit het middelpunt de rechten CA en CB worden getrokken. Aangezien dan het cirkelsegment ADB groter is dan vierderde van de ingeschreven driehoek ADB {* volgens 3. hier}, zullen de segmenten AD en DB samen groter zijn dan een derde van driehoek ADB. En daarom zal de sector CAB groter zijn dan de vierhoek CADB en een derde van driehoek ADB. Zoals nu sector CAB tot de hele cirkel is, zo is vierhoek CDBA tot veelhoek ADB, en zo ook is een derde van driehoek ADB tot een derde van het overschot van veelhoek ADB boven veelhoek AB. Dus is duidelijk dat ook de hele cirkel groter zal zijn dan veelhoek ADB samen met een derde van het overschot waarmee veelhoek ADB de veelhoek AB te boven gaat, dat wil zeggen samen met het oppervlak H. Wat te bewijzen was.

⁵) Met s_n als oppervlak van de veelhoek met n zijden, ingeschreven in een cirkel met straal 1, moet dus gelden: π > s_2n + ¹/₃ (s_2n – s_n).
Met p als omtrek van een veelhoek geeft s_2n = ½ p_n [^] de formule: 2 π > p_2n + ¹/₃ (p_2n – p_n). Vergelijk noot 7 van p. 94. Huygens verkreeg zo een benadering zoals Snellius (1621, p. 42-) op een veel ingewikkelder manier had bereikt.

[ 131 ]

Theor. VI. Prop. VI.
Elke cirkel is kleiner dan tweederde van een omgeschreven veelhoek met gelijke zijden en een derde van de gelijkvormige ingeschreven veelhoek.⁶)

Laat er een cirkel zijn met middelpunt A, en laat er worden ingeschreven een veelhoek met gelijke zijden, waarvan BC er een is; en omgeschreven een andere gelijkvormige FEG, waarvan de zijden aan de cirkel raken in de hoekpunten van de vorige veelhoek. Ik zeg dat de cirkel kleiner is dan tweederde van veelhoek FEG samen met een derde van veelhoek BC.
Want laat vanuit het middelpunt de rechten AB en AC worden getrokken. Aangezien dan op de basis van het segment BDC de driehoek BEC staat, waarvan de zijden aan het segment raken, zal dit zelf kleiner zijn dan tweederde van driehoek BEC {* volgens 4. hier}. Dus als aan driehoek ABC toegevoegd wordt tweederde van driehoek BEC, dat wil zeggen tweederde van het overschot van vierhoek ABEC boven driehoek ABC, zal het oppervlak uit beide samengesteld groter zijn dan de cirkelsector ABC. Nu is het hetzelfde, of aan driehoek ABC nu wordt toegevoegd tweederde van het genoemde overschot, of dat wordt toegevoegd tweederde van vierhoek ABEC en daarentegen afgetrokken tweederde van driehoek ABC; en hieruit komt tweederde van vierhoek ABEC met een derde van driehoek ABC. Dus blijkt dat sector ABC kleiner is dan tweederde van vierhoek ABEC en een derde van driehoek ABC. En daarom zal, als alles zoveel maal wordt genomen als sector ABC door de cirkel wordt omvat, ook de hele cirkel kleiner zijn dan tweederde van de omgeschreven veelhoek FEG en een derde van de ingeschreven veelhoek BC. Wat te bewijzen was.

⁶) Dus: π < ²/₃ S_n + ¹/₃ s_n , waarbij de straal 1 is. [...] Afgeleid kan worden dat de benadering van dezelfde orde is als bij het vorige theorema.

[ 133 ] [ 1654, 9 ]

Theor. VII. Prop. VII.
Elke cirkelomtrek is groter dan de omtrek van een ingeschreven veelhoek met gelijke zijden en een derde van het overschot waarmee deze omtrek de omtrek van een andere ingeschreven veelhoek, met de helft van het aantal zijden, te boven gaat.⁷)

Laat er een cirkel AB zijn, met middelpunt O, waarin de gelijkzijdige veelhoek ACD wordt ingeschreven, en ook een andere AECBDF met het dubbele aantal zijden. En laat de rechte GI gelijk zijn aan de omtrek van veelhoek AECBDF, maar GH gelijk aan de omtrek van veelhoek ACD. Het overschot van de omtrekken is dus HI; waarvan een derde deel KI wordt gedaan bij GI. Ik zeg dat de hele GK groter is dan de omtrek van cirkel AB.

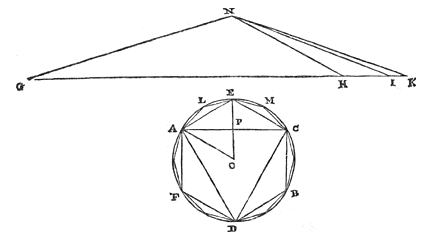
driehoek, cirkel met ingeschreven drie-, zes- en twaalfhoek

Immers: laat in de cirkel een derde gelijkzijdige veelhoek ALEMC ingeschreven worden, die het dubbele aantal zijden heeft van veelhoek AECBDF. En laat op de lijnen GH, HI en IK driehoeken worden opgericht waarvan de gemeenschappelijke top N is, en de hoogte gelijk aan de halve middellijn van cirkel AB. Aangezien dus de basis GH gelijk is aan de omtrek van veelhoek ACD, zal driehoek GNH gelijk zijn aan de veelhoek die tweemaal zoveel zijden heeft, dat is aan veelhoek AECBDF. Dit blijkt namelijk als vanuit het middelpunt de rechten OA en OE worden getrokken, waarvan de laatste AC snijdt in P. Want driehoek AEO is inderdaad gelijk aan een driehoek die als basis AP heeft en als hoogte de straal OE. En het zoveelste deel driehoek AEO is van veelhoek AECBDF, is ook de rechte AP van de omtrek ACD. Dus veelhoek AECBDF zal gelijk zijn aan een driehoek waarvan de basis gelijk is aan omtrek ACD, en de hoogte aan straal EO; dat is aan driehoek GNH.
Om dezelfde reden, aangezien basis GI gelijk is aan de omtrek van veelhoek AECBDF, en de hoogte van driehoek GNI gelijk aan de straal van de cirkel, zal driehoek GNI gelijk zijn aan veelhoek ALEMC. Dus driehoek HNI is gelijk aan het overschot van veelhoek ALEMC boven veelhoek AECBDF. En van driehoek HNI is door constructie driehoek INK een derde. Dus deze zal gelijk zijn aan een derde van genoemd overschot. En daarom zal de hele

⁷) Zie de tweede formule van noot 5.

[ 135 ]

driehoek GNK kleiner zijn dan cirkel AB {* volgens 5. hier}. Doch de hoogte van de driehoek is gelijk aan de halve middellijn van de cirkel. Dus het is evident dat de rechte GK kleiner is dan de hele cirkelomtrek. Wat te bewijzen was.

Hieruit is duidelijk: als van vierderde van de zijden van een in een cirkel ingeschreven veelhoek afgenomen wordt een derde van de zijden van een andere ingeschreven veelhoek met de helft van het aantal zijden, dan is de rest kleiner dan de cirkelomtrek. Het is immers hetzelfde, of aan de grotere omtrek nu toegevoegd wordt ¹/₃ van het overschot waarmee deze de kleinere omtrek te boven gaat, of dat wordt toegevoegd ¹/₃ van de grotere omtrek en integendeel weggenomen ¹/₃ van de kleinere omtrek. En hieruit komt vierderde van de grotere omtrek min een derde van de kleinere. En daarom, als van zestien zijden van de ingeschreven twaalfhoek twee zijden van de ingeschreven zeshoek, dat wil zeggen de middellijn van de cirkel, wordt afgetrokken, zal de rest kleiner zijn dan de cirkelomtrek of als van acht zijden van de twaalfhoek de straal wordt afgetrokken, zal de rest kleiner zijn dan de helft van de omtrek. En dit is nuttig voor mechanische constructie, aangezien het verschil gering is, zoals later zal worden aangetoond⁸).

Duidelijk is ook dat bij elke boog die kleiner is dan de halve omtrek, als bij de koorde wordt toegevoegd een derde van het overschot waarmee de koorde de sinus te boven gaat, het samengestelde kleiner zal zijn dan de boog.*)

⁸) Zie Problema II, Prop. XI, p. 143. [ *) Zie in de figuur: boog AE, sinus AP.]

Theor. VIII. Prop. VIII.
Als bij een gegeven cirkel aan het uiteinde van een middellijn een raaklijn wordt getrokken, en als ook van het tegenoverliggende uiteinde een lijn wordt getrokken die de omtrek snijdt en de getrokken raaklijn ontmoet: dan zal tweederde van het afgesneden stuk raaklijn, met een derde van de lijn die vanaf het snijpunt loodrecht op de middellijn valt, samen groter zijn dan de aanliggende afgesneden boog.⁹)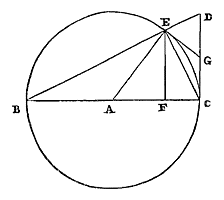

Laat er een cirkel zijn met middelpunt A en middellijn BC; en vanuit C wordt een rechte CD getrokken die aan de cirkel raakt; en deze wordt ontmoet door een andere rechte BD, getrokken vanaf het andere uiteinde van de middellijn, die de omtrek snijdt in E; en EF staat loodrecht op middellijn BC. Ik zeg dat tweederde van het afgesneden stuk raaklijn samen met een derde van die EF, groter zal zijn dan de boog EC.
Immers: laat verbonden woren AE en EC, en getrokken in het punt E een lijn die aan de cirkel raakt, die de raaklijn CD ontmoet in G. Dan zal GE gelijk zijn aan die GC, en evenzo aan DG; want als om G als middelpunt een omtrek wordt beschreven die door de punten C en E gaat, zal deze ook door het punt D gaan, aangezien de hoek CED recht is. Nu is hierboven bewezen dat tweederde van vierhoek AEGC met een derde van driehoek AEC samen groter is dan sector AEC {* volgens 6. hier}. En vierhoek AEGC is gelijk aan een driehoek die als basis heeft het dubbele van CG, dat is CD, en als hoogte CA; en driehoek

⁹) Het doel van dit theorema is vooral het voorbereiden van Theor. IX. Toch is duidelijk dat het directer leidt tot: Elke cirkelomtrek is kleiner dan tweederde van de omtrek van een omgeschreven gelijkzijdige veelhoek, plus een derde van de omtrek van de ingeschreven veelhoek met de helft van het aantal zijden.
Maar waarschijnlijk is dit theorema (vgl. 2e formule van noot 6) door Huygens beschouwd als minder elegant en minder praktisch dan Theor. IX dat hij laat volgen, waarvan bovendien de benadering iets beter is.

[ 137 ]

AEC is gelijk aan een driehoek die als basis heeft EF en als hoogte de genoemde AC. Dus blijkt tweederde van vierhoek AEGC samen met een derde van driehoek AEC gelijk te zijn aan een driehoek die als basis heeft de samengestelde uit tweederde van CD en een derde van EF, en als hoogte de straal AC. En daarom zal zo'n driehoek ook groter zijn dan sector AEC. Waaruit volgt dat de basis daarvan, dat is de samengestelde uit tweederde van CD en een derde van EF, groter is dan boog CE. Wat te bewijzen was.

Theor. IX. Prop. IX.
Elke cirkelomtrek is kleiner dan tweederde van de omtrek van een gelijkzijdige ingeschreven veelhoek en een derde van de omtrek van de gelijkvormige omgeschreven veelhoek.¹⁰)

Laat er een cirkel zijn met middelpunt A; en laat daarin worden ingeschreven een gelijkzijdige veelhoek, met zijde CD; en omgeschreven een gelijkvormige andere met de zijden evenwijdig aan de vorige, waarvan EF er een is. Ik zeg dat de omtrek van de hele cirkel kleiner is dan tweederde van de omtrek van veelhoek CD en een derde van de omtrek van veelhoek EF.
Want laat de middellijn BG van de cirkel worden getrokken, die tegelijk de zijde CD van de ingeschreven veelhoek doormidden deelt in H, en de zijde EF van de omgeschreven veelhoek in G (en het staat vast dat G het contactpunt van zijde EF zal zijn). En HL wordt gelijk aan HG gesteld, en AC en BC worden verbonden en verlengd, en BC ontmoet zijde EF in K, doch de verlengde van AC valt in het hoekpunt E van de omgeschreven veelhoek.
Aangezien dus HL gelijk is aan HG, zal BL het dubbele van AH zijn. En daarom geldt: zoals GA tot AH is, zo is GB tot BL. Nu is de verhouding van HB tot BL groter dan die van GB tot BH, aangezien de volgende drie elkaar met een gelijke waarde overtreffen: GB, HB en LB. Dus zal de verhouding van GB tot BL, dat wil zeggen van GA tot AH, groter zijn dan de kwadratische verhouding van GB tot BH.*)

¹⁰) Dit theorema is af te leiden uit het in noot 9 geformuleerde. [...] Wat volgt is via een kortere weg te vinden, zie noot 11.
[ *) B.v.: als GB = 10, HB = 9, LB = 8, dan is GB : BL = 10 : 8, en (GB : BH)² = (10 : 9)² = 100 : 81.]

[ 139 ]

En zoals GA tot AH is, zo is EG tot CH; en zoals GB tot BH, zo KG tot CH. Dus zal de verhouding van EG tot CH groter zijn dan de verdubbelde van die, welke KG tot CH heeft. En daarom is de verhouding van EG tot KG groter dan die van KG tot CH. Zodat de twee EG en CH samen zeker groter zijn dan het dubbele van KG¹¹). En als van alle het derde deel wordt genomen zullen de derde delen van EG en CH samen groter zijn dan tweederde van KG. Derhalve, met toevoeging van het derde van CH aan weerskanten, zal een derde van EG met tweederde van CH groter zijn dan tweederde van KG met een derde van CH. Maar ook is kleiner dan deze de boog CG {* volgens vorige}. Dus tweederde van CH samen met een derde van EG is zeker groter dan dezelfde boog CG. Dientengevolge, met alles zoveel maal genomen als boog CG door de hele omtrek wordt bevat, zal ook tweederde van van de omtrek van veelhoek CD met een derde van de omtrek van veelhoek EF, groter zijn dan de omtrek van de hele cirkel. Wat te bewijzen was.

Dus elke omtreksboog kleiner dan een vierde deel is kleiner dan tweederde van de sinus ervan en een derde van de tangens.

¹¹) Dit resultaat had makkelijker verkregen kunnen worden door een loodlijn CM op EG neer te laten. Dan is CK de bissectrice van hoek ECM en dus is EK > KM, d.w.z. EG – KG > KG – CH, dus EG + CH > 2 KG.

[ 1654, 15 ]

Probleem I. Prop. X.

Een verhouding van omtrek tot middellijn willekeurig dichtbij de ware te vinden.
Dat de verhouding van de omtrek tot de middellijn kleiner is dan drie en een zevende, maar groter dan 3¹⁰/₇₁, toonde Archimedes aan¹²) met een ingeschreven en een omgeschreven veelhoek met 96 zijden. Hetzelfde zullen we hier echter bewijzen met twaalfhoeken.

Omdat namelijk een zijde van de in een cirkel ingeschreven twaalfhoek groter is dan 5176³/₈ delen, waarvan de straal er 10000 bevat, zullen twaalf zijden derhalve, dat is de omtrek van de ingeschreven twaalfhoek, groter zijn dan 62116½; doch de omtrek van een ingeschreven zeshoek is zesmaal de straal, en daarom van 60000 delen. Dus overtreft de omtrek van de twaalfhoek de omtrek van de zeshoek met meer dan 2116½ delen. En daarom zal een derde deel van het overschot groter zijn dan 705½. Dus zal de omtrek van de twaalfhoek samen met een derde van het overschot, waarmee hij de omtrek van de zeshoek te boven gaat, groter zijn dan het samenvoegsel van 2116½ en 705½ delen, dat is 62822 delen. En ten opzichte van deze zal derhalve de cirkelomtrek zeker groter zijn {* volgens 7. hier}. Doch de verhouding van 62822 tot 20000, de lengte van de middellijn, is groter

¹²) Aangehaald in noot 1 op p. 93 [Heiberg I, 1880, 257-271].
[ Heath, 1897, p. 91-98. Huygens gebruikte ed. Basel 1544, Lat. p. 55-58.]

[ 141 ]

dan 3¹⁰/₇₁ tot 1. Dus zal de verhouding van de omtrek tot de middellijn zeker ook groter zijn.

Aan de andere kant, aangezien de zijde van de ingeschreven twaalfhoek kleiner is dan 5176²/₅ delen, zullen acht zijden, dat is ²/₃ van de omtrek, kleiner zijn dan 41411¹/₅ delen. Evenzo, omdat de zijde van de omgeschreven twaalfhoek kleiner is dan 5359, zullen vier zijden, dat is een derde van de omtrek, kleiner zijn dan 21436. Daarom zal ²/₃ van de omtrek van de ingeschreven twaalfhoek met een derde van de omtrek van de omgeschreven twaalfhoek kleiner zijn dan 62847¹/₅. Maar ten opzichte van deze samen is ook de cirkelomtrek kleiner {* volgens 9. hier}. Dus deze zal tot de middellijn zeker een kleinere verhouding hebben dan 62847¹/₅ tot 20000; en veel kleiner derhalve dan 62857¹/₇, dat is drie en een zevende.
Bewezen zijn dus de begrenzingen van de Verhouding van omtrek tot middellijn die Archimedes heeft vastgesteld. Die zelfde begrenzingen zullen we echter hierna bevestigen als alleen de zijde van de ingeschreven gelijkzijdige driehoek is opgespoord¹³). Verder, om de verhouding dichter te benaderen moeten veelhoeken met meer zijden beschouwd worden. We stellen ons dan voor een veelhoek bij de cirkel omgeschreven, en een andere ingeschreven, met 60 zijden. En bovendien een ingeschreven veelhoek met de helft van het aantal zijden, namelijk een dertighoek.

En dan wordt gevonden dat de zijde van een ingeschreven zestighoek groter is dan 10467191 delen, waarvan de straal er 100000000 heeft, en de zijde van de dertighoek kleiner dan 20905693; hiervan is de helft 10452846½ de sinus van de boog die gelijk is aan ¹/₆₀ van de omtrek. En de koorde was [groter dan] 10467191. Dus het verschil 14344½ is kleiner dan het ware; en een derde deel van het verschil is 4781½, wat opgeteld bij de koorde 10467191 geeft 10471972½. En groter dan dit is dus de boog van ¹/₆₀ van de omtrek*). Als nu 10471972½ wordt vermenigvuldigd met zestig komt er 628318350. De hele omtrek is dus zeker groter dan dit.

Aan de andere kant, aangezien de zijde van de ingeschreven 60-hoek kleiner is dan 10467192, zal tweederde ervan kleiner zijn dan 6978128. En aangezien de zijde van de omgeschreven 60-hoek kleiner is dan 10481556, zal een derde deel daarvan kleiner zijn dan 3493852. En als dit wordt opgeteld bij 6978128 komt er 10471980. Dit is dus zeker groter dan ¹/₆₀ van de omtrek, en het zestigvoudige ervan, dat is 628318800, zal groter zijn dan de hele omtrek.
En laten we zelfs veelhoeken toepassen met 10800 zijden, waarvan inderdaad de zijde van de ingeschreven veelhoek, door de berekening van de edele Rekenkundige Ludolph van Ceulen, is bevonden van 58177640912684919 delen en niet één meer, en deze strekt zich uit onder een boog van twee minuten; de zijde van de omgeschreven veelhoek nu is 58177643374063182 en niet één minder. En bovendien is de zijde van de ingeschreven veelhoek met de helft van het aantal zijden 116355276902613523 en niet één minder¹⁴). Hiermee wordt de lengte van de omtrek groter bevonden dan

¹³) Zie Probleem IV, p. 173. [ *) Zie p. 135: laatste alinea van Theor. VII.]
¹⁴) De zijden van de ingeschreven veelhoek staan in een tabel op fol. 21v van het werk genoemd op p. 93, n. 3 [Ludolph van Ceulen, Vanden circkel, 1596]. Voor de omgeschreven veelhoek is de tabel ernaast te gebruiken. [...]

[ 143 ]

6283185307179584 delen, en kleiner dan 6283185307179589, als de straal er 1000000000000000 heeft. Doch met de gebruikelijke methode door optelling van de zijden van deze ingeschreven en omgeschreven veelhoek, wordt alleen gevonden dat de omtrek groter is dan 62831852 delen en kleiner dan 62831855. Het blijkt dus dat het aantal ware cijfers door ons gevonden meer dan tweemaal zo groot is. En dit is ook het geval bij het voorgaande, en steeds moet het er uitkomen, hoe groot het aantal zijden ook is van de veelhoeken die we gebruiken. Maar met wat we hierna zullen behandelen zal blijken dat gemakkelijk een drievoudig aantal cijfers bereikt kan worden¹⁵).

¹⁵) [... Nagegaan wordt dat de bewering van Huygens klopt in bijna alle gevallen.]

Probleem II. Prop. XI.

Een rechte nemen die gelijk is aan de omtrek van een gegeven cirkel.
Hierboven is aangetoond¹⁶), dat acht zijden van een ingeschreven twaalfhoek verminderd met de straal van de cirkel, kleiner zijn dan de helft van de omtrek. Doch bij constructie kan meestal geen verschil worden opgemerkt. Want als er een vierduizendste deel van de middellijn bij de zo gevonden lengte komt, zal deze de helft van de omtrek al overtreffen. Wat als volgt duidelijk zal worden. Als de straal van 10000 delen is, is de zijde van de in de cirkel ingeschreven twaalfhoek groter dan 5176³/₈ van deze delen. Dientengevolge zijn acht zijden groter dan 41411; en als de straal 10000 eraf wordt gehaald, zal de rest groter zijn dan 31411. Als daarbij 5 delen worden opgeteld, dat is ¹/₄₀₀₀ van de middellijn, komen er al 31416 delen, en dat de halve omtrek kleiner is dan deze blijkt uit het voorgaande. Nu wordt de zijde van een ingeschreven twaalfhoek gemakkelijk gevonden, omdat de straal een zesde deel van de omtrek onderspant. En deze verhouding is nauwkeuriger dan wanneer we die van drie en een zevende gebruiken. Want volgens deze zal de ½¹⁷) lengte van de omtrek worden overtroffen met meer dan ¹/₁₆₀₀ van de middellijn.

¹⁶) Zie de voorlaatste alinea van Theor. VII, Prop. VII, p. 135 hierboven.
¹⁷) Het getal ½ is met pen ingevoegd in het exemplaar van Huygens, dat we bezitten.

[ 145 ]

Anders.
Gegeven een cirkel met BC als middellijn. De halve omtrek BC wordt in tweeën gedeeld in D, en de andere in drieën in E en F. En getrokken worden DE en DF, die de middellijn zullen snijden in G en H. Dan zal een zijde van driehoek GDH samen met de basis GH iets groter zijn dan het vierde deel BD, en dit namelijk met niet meer dan ¹/₅₀₀₀ van middellijn BC overtreffen.*)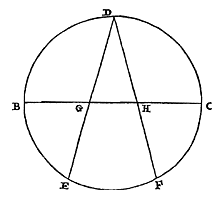
Te weten is namelijk dat DG of DH gelijk is aan twee zijden van een ingeschreven twaalfhoek¹⁸). En GH aan de zijde van de omgeschreven twaalfhoek¹⁹). Dientengevolge staat wel vast dat DG en GH samen groter zijn dan het vierde deel BD. Want omdat volgens 8.²⁰) hierboven acht zijden van de in de cirkel ingeschreven twaalfhoek met vier zijden van de omgeschrevene groter zijn dan de hele omtrek, daarom zullen, als van alles het vierde deel wordt genomen, ook twee zijden van de ingeschrevene met een zijde van de omgeschrevene groter zijn dan een vierde van de omtrek. Verder, aangezien een zijde van de ingeschreven twaalfhoek kleiner is dan 51764 delen waarvan BC er 200000 heeft, zullen twee zijden, dat is GD, kleiner zijn dan 103528. En de zijde van de omgeschreven twaalfhoek is kleiner dan 53590 delen, en dat is GH. Dus als DG en GH worden samengevoegd maken ze er minder dan 157118. Maar het vierde deel BD is groter dan 157079, zoals vaststaat uit het voorgaande. Dus het verschil is kleiner dan 39 delen, terwijl pas 40 delen ¹/₅₀₀₀ van middellijn BC maken.

[ *) Huygens schreef hierover aan Lipstorp en van Schooten in maart 1654, zie T. I, p. 274-276.]
¹⁸) Omdat hoek EDF = 30°, is ½ DH = ½ r : cos 15° = r sin 30° : cos 15° = 2 r sin 15 ° = a₁₂.
¹⁹) Als M het middelpunt is, heeft een andere cirkel, met straal DM en middelpunt D, een omgeschreven twaalfhoek met zijde GH, omdat EDF = 30°.
²⁰) Lees 9.

Anders.²¹)
Tel bij drie halve diameters op ¹/₁₀ van de zijde van een ingeschreven vierkant; het samengestelde zal de halve omtrek zo dicht benaderen, dat het geen ¹/₁₈₀₀₀²²) van de middellijn korter is. De zijde van het vierkant is groter dan 141421 delen waarvan de straal er 100000 heeft, zodat gemakkelijk is aan te tonen wat gezegd is.

Of liever: tel bij zes halve middellijnen op ¹/₅ van de genoemde zijde van het ingeschreven vierkant om een rechte te krijgen gelijk aan de hele omtrek.

²¹) Heel dit tweede 'Anders' staat niet in de gedrukte tekst [^], maar Huygens schreef het met pen in zijn exemplaar; het is niet bekend wanneer.
²²) Lees 1/11000. Het verschil is 1/11700 van de middellijn.

[ 147 ]

Probleem III. Prop. XII.

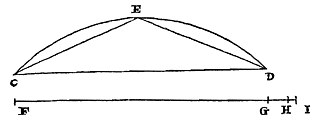
Een rechte nemen die gelijk is aan een willekeurige gegeven boog.
Gegeven een omtreksboog CD, eerst kleiner dan een vierde deel, waarbij een rechte moet worden genomen die eraan gelijk is.

Laat boog CD doormidden in E doormidden gedeeld worden, en laat een rechte FG gelijk zijn aan de koorde CD. En FH gelijk aan de twee CE en ED, die de koorden zijn van de booghelften. En aan deze FH wordt toegevoegd HI, een derde van het overschot GH. Dan zal de hele FI bijna gelijk zijn aan boog CD, zodanig dat hij groter zal zijn als hij wordt vergroot met één van zijn deeltjes, waarvan hij er 1200 bevat; ook als boog CD gelijk aan het vierde deel wordt gegeven. En bij kleinere bogen zal het verschil kleiner zijn. Want als hij niet groter is gegeven dan een zesde van de omtrek, zal de gevonden lijn met minder dan zijn ¹/₆₀₀₀ deel afwijken van de ware lengte van de boog. En dat de op deze wijze gevonden rechten inderdaad kleiner zijn dan de bogen staat vast uit Theorema 7 hierboven. Doch over de grootte van het verschil is nog iets te bewijzen.

Door dus eerst de boog CD gelijk te stellen aan een vierde van de omtrek, zal de rechte CD, dat is FG, een zijde zijn van een in de cirkel ingeschreven vierkant, en derhalve kleiner dan van 141422 delen, waarvan de straal van de cirkel er 100000 heeft. En CE of ED een zijde van een ingeschreven achthoek, en daarom groter dan 76536. Nu is tweemaal ED gelijk aan FH. Dus deze is groter dan 153072. En daarom is het overschot GH groter dan 11650; en het derde deel hiervan HI groter dan 3883. En daarom is de hele FI groter dan 156955. Doch daar boog CD kleiner dan het vierde deel wordt gesteld is hij kleiner dan 157080. Dus hiervan verschilt de rechte FI minder dan 125 delen, waarvan deze er zelf 156955 heeft. Wat in elk geval minder is dan ¹/₁₂₀₀ van FI zelf.

Als boog CD echter een zesde deel van de omtrek is, zal de rechte CD, dat is FG, een zijde zijn van een ingeschreven zeshoek, en daarom van 10000 delen, en CE of ED een zijde van een twaalfhoek, en daarom groter dan 5176³/₈; waarvan het dubbele FH groter is dan 10352¾; dientengevolge is GH groter dan 352¾ en HI groter dan 117⁷/₁₂. De hele FI is dus groter dan 10470¹/₃. Doch boog CD, een zesde van de omtrek, is kleiner dan 10472. Dus ontbreken aan de lijn FI minder dan 1²/₃ van dezelfde delen. Wat nog geen ¹/₆₀₀₀ van FI is.
Verder, wanneer de boog groter is gegeven dan een vierde, moet hij worden verdeeld in 4 of 6 of meer gelijke delen, naar gelang we een nauwkeurige afmeting willen gebruiken; maar van even getallen. En als de koorden van deze delen worden samengenomen moet er bijgevoegd worden een derde van het overschot waarmee zij het samenvoegsel te boven gaan van de koorden bij steeds twee bogen. Want zo

[ 149 ]

zal de lengte van de hele boog worden samengesteld. Of dit kan ook op dezelfde manier verkregen worden, als de lengte gevonden wordt van de resterende boog op de halve omtrek, of het overschot daarboven, of van de resterende boog op de hele omtrek, als er een gegeven is die groter is dan drievierde; en deze lengte wordt toegevoegd aan of weggenomen van de lengte van de halve of de hele omtrek, waarvan we eerder hebben uiteengezet hoe die is te vinden.

Theor. X. Prop. XIII.
De zijde van een in de cirkel ingeschreven gelijkzijdige Veelhoek, is middelevenredig tussen de zijde van de gelijkvormige omgeschreven veelhoek, en de halve zijde van de ingeschreven veelhoek met het halve aantal zijden.²³)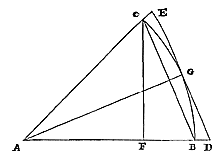

Laat in een cirkel met middelpunt A en straal AB de zijde van een ingeschreven gelijkzijdige veelhoek BC zijn; en de zijde van de gelijkvormige omgeschreven veelhoek DE, evenwijdig aan BC.
Dus zal de verlengde AB gaan door D, en AC door E. En als CF loodrecht op AB wordt getrokken, zal deze de helft zijn van de zijde van de ingeschreven veelhoek met het halve aantal zijden. Daarom moet worden aangetoond dat BC middelevenredig is tussen ED en CF.
Laat getrokken worden AG, die ED doormidden deelt, en daarom ook de halve middellijn zal zijn van de cirkel en gelijk aan AB. En aangezien geldt: zoals ED tot CB is, zo is DA tot AB, dat wil zeggen DA tot AG; en zoals DA tot AG is, zo is BC tot CF, vanwege de gelijkvormige driehoeken DAG en BCF. Derhalve zal gelden: zoals ED tot CB is, zo is ook CB tot CF. Wat te bewijzen was.

²³) Er geldt dus: p²_2n = p_n P_2n. Zie p. 94, noot 7 voor het verband met Prop. IX van Snellius [Cyclometricus, p. 14].

Lemma. ²⁴)
Laat een lijn BC gelijk verdeeld zijn in R; en ongelijk in F, met het grootste segment FC; laat BO gelijk zijn aan BC en CF samen; en BM aan BC en CR. Ik zeg dat de verhouding van RB tot BF groter is dan de verdrievoudigde van die, welke OB tot BM heeft.

Immers: laat gelijk aan OM worden genomen elk van deze twee: ML en LP. Aangezien dan MO gelijk is aan RF (want dit wordt door de constructie verondersteld) zal PO het drievoudige zijn van FR. Maar ook is BM het drievoudige van BR. Dus zoals BR tot BM is, zo is FR tot PO. En door verwisseling: zoals BR tot FR is, zo is BM tot PO. Nu is BO groter dan BM. Dus zal de verhouding van BO tot OP groter zijn dan die van BR tot RF; en door omzetting van de verhouding:

²⁴) Ter voorbereiding van Theor. XI, waaraan Huygens zoveel waarde hechtte, zie p. 97, n. 17.
[ Theor. XI wordt al genoemd in het Voorwoord, p. 115 en in brieven: T. 1, p. 279, 290 aan Kinner; p. 281 (eind) aan Gregorius; p. 289 aan Golius.]
Stel BR = a en RF = x, dan geldt voor x < a:
a / (a – x) > {(3a + x) / 3a}³ , of, zo men wil: 1 / (1 – ζ) > (1 + ζ/3)³ , met ζ < 1.

[ 151 ]

OB tot BP is kleiner dan RB tot BF²⁵). Verder, aangezien OM en ML gelijk zijn, zal de verhouding van BO tot OM groter zijn dan die van BM tot ML; en door omzetting van de verhouding: OB tot BM kleiner dan MB tot BL. Op dezelfde manier is nog aan te tonen dat de verhouding van MB tot BL kleiner is dan die van LB tot BP. Dus zal de verdrievoudigde verhouding van die van OB tot BM zeker kleiner zijn dan de samengestelde uit de verhoudingen van OB tot BM, BM tot BL, en BL tot BP, dat wil zeggen dan de verhouding van OB tot BP. Nu was RB tot BF groter dan OB tot BP. Dus zal de verhouding RB tot BF zeker groter zijn dan de verdrievoudigde verhouding van OB tot BM. Wat te bewijzen was.

²⁵) Huygens gebruikt hier, en ook later, een stelling uit de theorie van verhoudingen:
als a > b en c > d dan volgt uit a/b > c/d dat ook geldt a / (a – b) < c / (c – d).

[ 1654, 23 ]

Theor. XI. Prop. XIV.
Elke cirkelomtrek is kleiner dan de kleinste van twee middelevenredigen tussen de omtrekken van gelijkvormige veelhoeken, waarvan de ene bij de cirkel regelmatig is ingeschreven, de andere omgeschreven. En de cirkel is kleiner dan een daarmee gelijkvormige veelhoek waarvan de omvang gelijk is aan die van de grootste van de middelevenredigen.²⁶)

Laat de cirkel zijn BD, met middelpunt A. En laat er ingeschreven worden de gelijkzijdige veelhoek BCDL, en omgeschreven een gelijkvormige HKMN, met de zijden evenwijdig. Aan de omtrek van veelhoek HKMN is gelijk de rechte T, en aan de omtrek van BCDL is Z gelijk. En tussen Z en T zijn X en V twee middelevenredigen, waarvan X de kleinste is. Ik zeg dat de omtrek van cirkel BD kleiner is dan de rechte X. En als er een veelhoek Y is, waarvan de omtrek gelijk is aan de rechte V, en die gelijkvormig is

²⁶) Zie voor het eerste deel p. 97 [...] en voor het tweede deel p. 115, n. 1. [...]

[ 153 ]

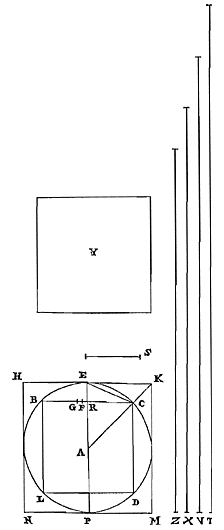met BCDL of HKMN, dan zeg ik dat cirkel BD kleiner is dan de veelhoek Y.
Immers: laat getrokken worden de middellijn PE van de cirkel, die de evenwijdige zijden BC en HK, van de ingeschreven en omgeschreven veelhoek, doormidden deelt in R en E; dan zal E het contactpunt zijn van de zijde HK, en BC zal in R loodrecht worden gesneden. Laat ook vanuit het middelpunt worden getrokken de rechte ACK, die de hoeken C en K van beide veelhoeken doormidden snijdt, want dat dit door deze rechte wordt gedaan staat vast; en laat CE verbonden worden.
Dan wordt aan deze CE gelijk gesteld CF; en laat bij deze twee, CR en CF, de derde evenredige zijn CG. Dus zoals CE of CF een zijde is van een ingeschreven veelhoek, zo zal CG het zijn van een omgeschreven veelhoek {* volgens 13. hier}. En daarom zal tweederde van CF samen met een derde van CG groter zijn dan de boog EC {* volgens 9. hier}.
Laat nu aan tweederde van CF met een derde van CG gelijk zijn de rechte S. Dus zal ook deze groter zijn dan boog EC.

En aangezien CR zich verhoudt tot CF als CF tot CG, zal ook gelden: tweemaal CR samen met CF tot driemaal CR (dat is BC met CF) verhoudt zich tot BC met CR, als tweemaal CF samen met CG tot driemaal CF; of als van deze het derde deel wordt genomen, als ²/₃ CF samen met ¹/₃ CG tot CF, dat is zoals S tot CF.
Daarom zal ook de verdrievoudigde verhouding van BC met CF tot BC met CR dezelfde zijn als de verdrievoudigde verhouding van S tot CF. Nu is de verhouding van RB tot BF groter dan de verdrievoudigde van BC met CF, tot BC met CR {* volgens voorgaand lemma}. Dus is dezelfde verhouding van RB tot BF groter dan de verdrievoudigde van S tot CF, dat wil zeggen van kubus S tot kubus CF. En zoals RB tot BF is, zo is kubus RB tot wat ontstaat uit vierkant RB maal BF. Dus is ook de verhouding van kubus RB tot vierkant RB maal BF groter dan van kubus S tot kubus CF.*)
Maar kleiner dan vierkant RB maal BF is de rechthoek op RB en BG, maal FC; wat als volgt wordt aangetoond. Omdat namelijk evenredig zijn RC, CF en CG, zal hetgene waarmee de grootste de middelste overtreft, dat is FG, groter zijn dan waarmee de middelste de kleinste overtreft, dat is FR. En FC is groter dan FB. Dus de verhouding van CF tot FR zal zeker groter zijn dan die van BF tot FG. En door omzetting van de verhouding: de verhouding van FC tot CR is kleiner dan die van FB tot BG²⁵). En door verwisseling: FC tot FB is kleiner dan CR of RB tot BG, dat is (als BR genomen wordt als gemeenschappelijke hoogte) dan van vierkant RB tot rechthoek RBG. Dientengevolge zal wat ontstaat uit rechthoek RBG maal FC kleiner zijn dan wat ontstaat uit vierkant RB maal FB, zoals gezegd is.
Daar dus is aangetoond dat de verhouding van kubus RB tot vierkant RB maal BF groter is dan die van kubus S tot kubus CF, zal zeker

[ *) T. 1, p. 289: Huygens verontschuldigt zich in zijn aanbiedingsbrief aan Jacob Golius voor een bewijsvoering met lichamen bij een vlak probleem. Hij beroept zich op Archimedes.]

[ 155 ]

ook de verhouding van kubus RB tot het blok van rechthoek RBG maal FC groter zijn dan die van kubus S tot kubus CF. En door verwisseling: de verhouding van kubus RB tot kubus S is groter dan die van rechthoek RBG maal FC, tot kubus CF; dat is groter dan rechthoek RBG tot vierkant CF. Nu is aan vierkant CF gelijk de rechthoek GCR, dat is de rechthoek op GC en RB, omdat evenredig zijn CR, CF en CG. Dus zal de verhouding van kubus RB tot kubus S groter zijn dan die van rechthoek RBG tot de rechthoek op GC en RB, dat is groter dan BG tot GC.
Zoals nu BG tot GC is, zo is RC tot EK. Immers: omdat CR tot CG is, als vierkant CR tot vierkant CF of vierkant CE; en zoals vierkant CR tot vierkant CE is, zo is PR tot tot middellijn PE. Daarom zal CR tot CG zijn als PR tot PE. Dientengevolge is het dubbele van CR, dat is CB, tot CG als het dubbele van PR tot PE, dat is als PR tot PA. En door verdeling: BG tot GC, als RA tot AP, of AE, dat wil zeggen als RC tot EK, wat we zeiden.
Dus is ook de verhouding van kubus RB tot kubus S, dat is de verdrievoudigde verhouding van RB tot S, groter dan RC tot EK. Doch aangetoond is dat S groter is dan boog EC. Dus zal de verdrievoudigde verhouding van RB of RC tot iets dat gelijk is aan boog EC zeker groter zijn dan RC tot EK. Zoals nu RC tot boog EC is, zo is de omtrek van veelhoek BCDL, dat is lijn Z, tot de omtrek van cirkel BD. En zoals RC tot EK is, zo is de omtrek van veelhoek BCDL tot de omtrek van veelhoek HKMN, dat wil zeggen: zo is Z tot T. Dus is ook de verdrievoudigde verhouding van Z tot de hele omtrek van BD groter dan Z tot T. Doch de verdrievoudigde verhouding van Z tot X is dezelfde als de verhouding van Z tot T. Dus is de verhouding van Z tot de genoemde omtrek groter dan die van Z tot X. En derhalve is de omtrek kleiner dan X. Wat te bewijzen was.

Nu is te weten dat die X kleiner is dan tweederde van Z en een derde van T, dat wil zeggen dan tweederde van de omtrek van de ingeschreven veelhoek en een derde van de omgeschreven veelhoek, en hiervan staat al vast uit het voorgaande dat de cirkelomtrek kleiner is dan dit²⁷). Want ²/₃ Z met ¹/₃ T is gelijk aan de kleinste van de twee middelevenredigen volgens een Rekenkundige verhouding, die groter is dan de kleinste van de middelevenredigen volgens een Meetkundige verhouding.
Dan zullen we het nu ook voor de veelhoek Y bewijzen, dat deze namelijk groter is dan de cirkel BD. Omdat immers veelhoek Y tot de gelijkvormige veelhoek HKMN de kwadratische verhouding heeft van die van omtrek tot omtrek; en omdat de omtrek van veelhoek Y gelijk is aan de rechte V, en de omtrek van HKMN aan T, zal derhalve veelhoek Y tot veelhoek HKMN de kwadratische verhouding hebben van die van V tot T, dat is de verhouding van X tot T.
Zoals nu veelhoek HKMN tot cirkel BD, zo is de omtrek van deze veelhoek, dat is de lijn T, tot de omtrek van cirkel BD; aangezien de veelhoek gelijk is aan een driehoek met de basis gelijk aan zijn omtrek en de hoogte van straal AE, doch de cirkel is gelijk aan een driehoek met dezelfde hoogte waarvan de basis gelijk is aan de cirkelomtrek. Volgens de gelijkheden zal dus veelhoek Y tot cirkel BD zijn als X tot omtrek BD²⁸). En aangetoond is dat X groter is dan omtrek BD. Dus zal ook veelhoek Y groter zijn dan cirkel BD. Wat te bewijzen was.

²⁷) Volgens Prop. IX, p. 137, al hierboven aangehaald.
²⁸) Vergelijk noot 1 van p. 115 hierboven.

[ 157 ]

Hieruit is de fout van Oronce Finé²⁹) duidelijk, die heeft meegedeeld dat een vierde deel van de omtrek gelijk was aan de kleinste van van de twee middelevenredigen tussen de zijden van het ingeschreven en omgeschreven vierkant, en de cirkel gelijk aan het vierkant dat ontstond uit de grootste.

²⁹) Oronce Finé (of Fine, of Orontius Finaeus; 1494-1555), Quadratura Circuli (1544), p. 13. [...] Alleen het tweede, over het oppervlak, wordt daar gevonden. Er moet wel een ander exemplaar of een andere editie zijn waarin het eerste staat, want Pedro Nunes, De erratis Orontii Finaei (1546) noemt het op p. 28. [...]

[ Andere editie, zie IMSS en ECHO (bij Arithmetica practica), eveneens van 1544, met p. 11.2: "... praeterea quadratum cg, eidem circulo ah/ esse isoperimetrum.", dat bovendien vierkant cg gelijke omtrek heeft met cirkel ah; zie Problema 5, op p. 15 .. 20-22. Het jaar is hetzelfde, maar het blijkt een latere editie:
- de Index is gelijk (zie andere), maar niet juist voor de laatstgenoemde,
- na 'Finis' staat er nu (p. 24): "... multa in melius commutavimus ...", we hebben veel verbeterd.
Eind van Praefatio: "malevolis ... obtrectatoribus, perpetuum invidiae tormentum exoptamus" is vervangen door (p. 3): " ... obtrectatoribus, meliorem mentem (ut Christianum decet philosophum) exoptamus" — "kwaadwillige ... benijders, wensen we een voortdurende kwelling van afgunst toe" werd: "... benijders, wensen we (zoals een Christelijk filosoof betaamt) een betere mening toe".]
[ Andere kritiek: Johannes Buteo, Opera geometrica, Lugd. 1554 (en 1559), p. 42-50.]

Het is niet de eerste, en ook niet de laatste foute kwadratuur van Oronce Fine, zie Protomathesis (1532), vol. 2, fol. 90 en De rebus mathematicis (1556).

Theor. XII. Propos. XV.
Als tussen een verlengde middellijn van de cirkel en de omtrek een rechte wordt gepast die gelijk is aan de straal, en waarvan het verlengde de cirkel snijdt, en die de lijn ontmoet die aan de cirkel raakt in het andere uiteinde van de middellijn; dan zal deze een deel van de raaklijn afsnijden dat groter is dan de aanliggende afgesneden boog.³⁰)

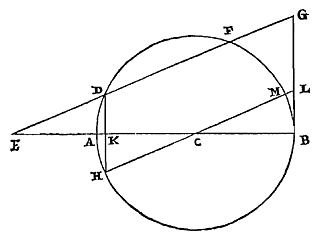
Laat een cirkel beschreven zijn om het middelpunt C, met middellijn AB. En deze wordt verlengd bij A, en tussen deze en de omtrek wordt een rechte ED geplaatst die gelijk is aan straal AC. Deze snijdt na verlenging de omtrek in F, en ontmoet de raaklijn in G, namelijk de lijn die aan de cirkel raakt in uiteinde B van de middellijn. Ik zeg dat de raaklijn BG groter is dan de boog BF.
Immers: laat getrokken worden door het middelpunt de rechte HL evenwijdig aan EG, die de omtrek ontmoet in de punten H en M, en de raaklijn BG in L. En laat verbonden worden DH, die de middellijn snijdt in K. Dan zijn de driehoeken EDK en CHK gelijkvormig, aangezien ze de hoeken bij K gelijk hebben, en hoek E gelijk aan hoek C. Maar ook is de zijde ED gelijk aan de zijde HC, en deze zijden liggen tegenover gelijke hoeken. Dus is ook de zijde DK gelijk aan de zijde KH. CA snijdt daarom DH doormidden, en eveneens de boog DAH. Dan is boog DH of de aan deze gelijke FM het dubbele van boog AH. Doch aan deze AH is gelijk de boog MB. Dan zal boog FB het drievoudige zijn

³⁰) Dit theorema is identiek met Prop. XXIX van Snellius, en verschilt niet essentieel van Theor. IX, Prop. IX van p. 137 hierboven. Zie de twee eerste formules van noot 10 op p. 136.

[ 159 ]

van boog AH. Verder, aangezien HK de sinus is van boog HA, en aan de tangens hiervan LB gelijk is, zullen tweederde van HK en een derde van LB samen groter zijn dan boog AH {* volgens 9. hier³¹)}. En daarom, als van alles een derde genomen wordt, zal het dubbele van HK, dat is HD of GL, samen met LB groter zijn dan het drievoudige van boog AH, dat wil zeggen groter dan boog FB. Dus blijkt de hele GB groter te zijn dan boog FB.

Dit Theorema is een van de twee, waarop de hele Cyclometria van Willebrord Snellius berust, en hij heeft gewild dat men dacht dat hij het had bewezen, met gebruikmaking van een betoog dat louter een cirkelredenering bevat³²). Maar we zullen ook het andere toevoegen, dat bij uitstek nuttig is en zeer het beschouwen waard.

³¹) Zie de laatste alinea van Theor. IX, Prop. IX, p. 139 hierboven.
³²) Het gaat om Prop. XXIX en Prop. XXVI: het speciale geval dat EG aan de cirkel raakt. [...]

Theor. XIII. Propos. XVI.
Als aan een middellijn van een cirkel een halve middellijn wordt toegevoegd, en vanaf het uiteinde van het toegevoegde wordt een rechte getrokken die de cirkel snijdt, en die de lijn ontmoet die aan de cirkel raakt in het tegenoverliggende uiteinde van de middellijn, dan zal deze een deel van de raaklijn afsnijden dat kleiner is dan de aanliggende afgesneden boog.³³)

³³) Het theorema is eigenlijk identiek met Prop. XXVIII van Snellius, wiens bewijs onjuist is. [...]
[ Kanttekeningen van Huygens in zijn vader's exemplaar van Cyclometricus bij deze Prop. (p. 42): "Haec propositio vera est et a nobis demonstrata ..." en (p. 43) "Hoc non aliter demonstrat Auctor, quam sumpto id quod erat demonstrandum ...", zie 'Huygens in Leiden' (2018), 2.11.]

[ 161 ]

Laat er een cirkel zijn met middellijn AB, die verlengd wordt, en AC is gelijk aan de halve middellijn. En getrokken wordt de rechte CL, die de omtrek voor de tweede maal snijdt in E, en de raaklijn ontmoet in L, namelijk die welke aan de cirkel raakt in uiteinde B van de middellijn. Ik zeg dat de afgesneden BL kleiner is dan de boog BE.

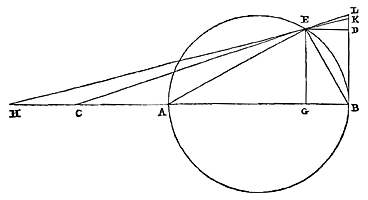
Immers: laat verbonden worden AE en EB en, met AH gelijk aan AE gesteld, wordt HE getrokken en verlengd, en hij ontmoet de raaklijn in K. Tenslotte moet EG loodrecht staan op middellijn AB, en ED op raaklijn BL. Aangezien dan de driehoek HAE gelijkbenig is, zullen de hoeken H en HEA aan elkaar gelijk zijn. En omdat de hoek AEB recht is, zullen ook aan een rechte hoek gelijk zijn de twee HEA en KEB samen. Maar ook deze twee H en HKB zijn samen gelijk aan een rechte hoek, aangezien in driehoek HKB de hoek B recht is. Als dus gelijke worden weggenomen aan weerskanten, namelijk hoek H van de laatste en hoek HEA van de eerste, zullen onderling gelijke hoeken KEB en HKB overblijven. Driehoek KBE is dus gelijkbenig, en de zijden EB en BK ervan zijn gelijk.
Nu is BD gelijk aan EG. Dus DK is het verschil waarmee BE EG overtreft. Verder, aangezien geldt dat AG tot AE is als AE tot AB, zullen de twee samen AG en AB groter zijn dan het dubbele van AE {* 25.5. Elem.³⁴)}. En daarom is AE, dat is AH, kleiner dan de helft van AG en AB samen, dat wil zeggen kleiner dan CA met de helft van AG. En daarom, als aan weerskanten CA er wordt afgenomen, zal CH kleiner zijn dan de helft van AG. CA is echter groter dan de helft van AG. Dus als AC bij AG wordt opgeteld, zal de hele CG groter zijn dan driemaal CH.
Omdat nu geldt dat zoals HG tot GE is, zo is ED tot DK; en zoals GE tot GC is, zo is LD tot DE; zal volgens de regel van de veranderde verhouding³⁵) gelden: zoals HG tot GC is, zo is LD tot DK. En door omzetting van de verhouding en verdeling, zoals GC tot CH is, zo is DK tot KL. Dus is DK ook groter dan driemaal KL. Nu was DK het overschot van EB boven EG. Dus KL is kleiner dan driemaal het genoemde overschot. En KB is gelijk aan de koorde EB. Dus zal KB samen met KL, dat is de hele LB, zeker kleiner zijn dan boog BE {* volgens 7. hier³⁶)}. Wat te bewijzen was.

En bij nauwkeurig afwegen van het voorgaande Theorema blijkt dat er geen ander punt kan worden genomen op de verlengde middellijn BA, dat minder ver van de cirkel ligt dan punt C, en dat dezelfde eigenschap heeft, namelijk dat na het trekken van CL de afgesneden raaklijn BL altijd kleiner is dan de afgesneden boog BE³⁷).

³⁴) Als vier grootheden evenredig zijn, zullen de grootste en de kleinste groter zijn dan de overige twee (Clavius, p. 518).
³⁵) Zie T. XI, p. 304, noot 22. [Clavius, p. 515; als a : b = e : f, en b : c = d : e, dan is a : c = d : f.]
³⁶) Zie de laatste alinea van het bewijs van Theor. VII, p. 135 hierboven.
³⁷) [... De uitspraak wordt bewezen.]

[ 163 ]

Verder is het gebruik van dit Theorema veelvoudig, zowel bij het vinden van hoeken van driehoeken waarvan de zijden bekend zijn, en dit zonder hulp van tabellen, als ook dat zijden gevonden worden uit bekende hoeken, of dat aan een willekeurige boog de koorde wordt toegekend. Dit alles is door Snellius in de Cyclometricus zorgvuldig behandeld³⁸).

³⁸) Zie in de 'Appendicula' de problemen V en VI, p. 95-102 en Prop. XXXVIII op p. 76-83. [...]

[ 1654, 31 ]

Theor. XIV. Propos. XVII. ³⁹)
Het zwaartepunt van een cirkelsegment verdeelt de middellijn van het segment zodanig, dat het deel bij de top groter is dan het overige deel, doch kleiner dan anderhalf maal zo groot.

Laat er een cirkelsegment ABC zijn (doch kleiner gesteld dan de halve cirkel, aangezien de andere niet van toepassing zijn op het voorgestelde), en de middellijn van het segment is BD, die doormidden wordt gesneden in E. Aangetoond moet dus worden dat ten eerste het zwaartepunt van segment AB verder dan E van de top verwijderd is; want dat het is gelegen op de middellijn hebben we elders aangetoond⁴⁰).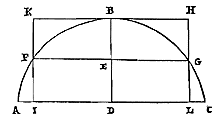
Laat door E een rechte getrokken worden evenwijdig aan de basis, die de omtrek aan weerskanten ontmoet in de punten F en G. Daardoor worden getrokken KI en HL, loodrecht op de basis AC, en samen met de lijn die in de top aan het segment raakt brengen deze de rechthoek KL tot stand. Aangezien het segment dus kleiner is dan de halve cirkel, staat vast dat de helft FL van de genoemde rechthoek binnen het segment AFGC is bevat, en bovendien enkele oppervlakken AFI en LGC. En dat de andere helft KG van de rechthoek KL het segment FBG insluit samen met de oppervlakken FBK en BGH. En daar deze oppervlakken geheel boven de rechte FG liggen, zal ook hun gemeenschappelijk zwaartepunt daarboven liggen. Dus het zwaartepunt van de rest BFILGB zal onder de rechte FG liggen. Maar ook het gemeenschappelijk zwaartepunt van de oppervlakken AFI en LGC ligt onder dezelfde FG. Dus van de grootheid die is samengesteld uit deze oppervlakken en het genoemde oppervlak BFILGB, dat is segment ABC zelf, wordt het zwaartepunt noodzakelijk onder lijn FG gevonden, en daarom onder het punt E.

³⁹) Zie p. 97 en 98 van het Voorbericht. [Brief No. 185 (I, 279) aan van Schooten.]
⁴⁰) Zie Theorema IV van Theorema's over de kwadratuur, p. 295 van T. XI.

[ 165 ]

Laat echter nu dezelfde middellijn BD gesneden worden in S, zodanig dat BS anderhalf maal het overige deel SD is. Ik zeg dat het zwaartepunt van segment ABC minder ver van de top B is verwijderd dan punt S.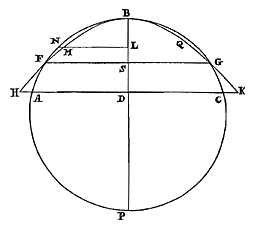
Immers: laat BDP de middellijn zijn van de hele cirkel, en door S een rechte getrokken worden evenwijdig aan de basis, die de omtrek ontmoet in F en G. En we stellen ons een parabool voor met B als top en BD als as, en het latus rectum gelijk aan SP. En hij ontmoet de basis van het segment in H en K. Aangezien dan het kwadraat van FS gelijk is aan de rechthoek BSP, dat wil zeggen aan die welke door BS en het latus rectum van de parabool wordt gemaakt, zal deze door punt F gaan, en evenzo door G. En de delen BF en BG van de parabolische lijn vallen binnen de omtrek, maar de overige FH en GK zullen erbuiten zijn.
Dit is namelijk aan te tonen als tussen B en S een langs de ordinaat gelegde NL is getrokken, die de omtrek ontmoet in N, en de parabool in M. Want omdat het kwadraat van NL gelijk is aan de rechthoek BLP, en het kwadraat van ML aan de rechthoek omvat door de lijnen BL en SP; en omdat rechthoek BLP groter is dan die door BL en SP wordt omvat; zal het kwadraat van NL groter zijn dan het kwadraat van ML, en lijn NL groter dan ML. En hetzelfde zal gebeuren overal waar tussen B en S een lijn langs de ordinaat wordt gelegd. Dus is het noodzakelijk dat het deel BF van de omtrek helemaal buiten de parabool loopt, en om dezelfde reden deel BG.
Aan de andere kant, omdat de rechthoek BDP gelijk is aan het kwadraat van DA, en de rechthoek omvat door BD en SP aan het kwadraat van DH, zal HD groter zijn dan AD in een macht, en daarom ook in lengte. En dezelfde uitkomst is er, waar ook tussen S en D een lijn langs de ordinaat wordt gelegd. En daarom zullen de delen van de omtrek FA en evenzo GC binnen de parabool vallen.
Er ontstaan dus enige oppervlakken FNBM en BQG, en evenzo andere HFA en GCK. En van de laatste zal, daar ze geheel onder de lijn FG liggen, ook hun gemeenschappelijk zwaartepunt onder deze lijn liggen. Maar van het paraboolsegment HBK is het zwaartepunt op FG zelf, namelijk het punt S {* 8. lib. 2. Archim. de Æquipond.⁴¹)}. Dus zal van het overige deel AFMBQGC het zwaartepunt boven de rechte FG liggen. Maar hierboven blijkt ook het zwaartepunt van de oppervlakken FMBN en BQC te zijn gelegen, daar ze helemaal boven FG liggen. Dus ook van het oppervlak dat uit deze twee en AFMBQGC is samengesteld, dat is van het cirkelsegment ABC, zal het zwaartepunt boven de lijn FG gevonden worden; en daar het ligt op de middellijn BD, zal het minder ver van de top B verwijderd zijn dan punt S. Wat te bewijzen was.

⁴¹) P. 138 van de Latijnse tekst, ed. Basel 1544. [...]
[ De methode van dit theorema wordt aangehaald in Is. Barrow, Lectiones, zie Engl. 1916, App.
Zoals ook het 3e en 4e theorema, zie T. VII, 38 en 43.]

[ 167 ]

Theor. XV. Propos. XVIII.
Een cirkelsegment kleiner dan de halve cirkel heeft tot de grootste ingeschreven driehoek een verhouding groter dan vierderde; en kleiner dan die van drie-eenderde maal de middellijn van het overige segment, tot de middellijn van de cirkel met driemaal het lijnstuk vanaf het middelpunt tot de basis van het segment.⁴²)

Gegeven het cirkelsegment ABC, kleiner dan de halve cirkel, met de grootste ingeschreven driehoek. Verder is de middellijn van het segment BD, en de middellijn van de cirkel waarvan het segment is gesneden is BF, het middelpunt is E. Aangetoond moet worden ten eerste, dat de verhouding van segment ABC tot de ingeschreven driehoek groter is dan vierderde.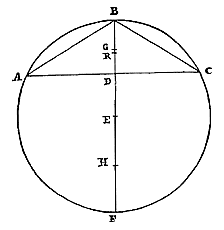
Laat het zwaartepunt van segment ABC het punt G zijn, en DF verdeeld worden in H, zodat HD het dubbele is van de rest HF. Aangezien dus FB het dubbele is van EB, en DB kleiner dan het dubbele van GB⁴³), zal de verhouding van FB tot BD groter zijn dan die van EB tot BG. En door omzetting van de verhouding: BF tot FD kleiner dan BE tot EG⁴⁴). En door te verwisselen: BF tot BE (welke verhouding twee op een is) kleiner dan FD tot EG. Dus FD is groter dan het dubbele van EG. Doch tweederde van deze FD bevat HD. Dus HD is groter dan vierderde maal EG. Zoals nu HD tot EG is, zo is segment ABC tot de ingeschreven driehoek; dit hebben we namelijk vroeger bewezen in de Theorema's over de kwadratuur van Hyperbool, Ellips en Cirkel⁴⁵). Dus is de verhouding van het segment tot de ingeschreven driehoek groter dan vierderde.

Verder, dat het segment tot de driehoek ABC een kleinere verhouding heeft dan die van drie en een derde van DF, tot de middellijn van de cirkel BF samen met driemaal ED, dit zullen we nu aantonen. Laat de middellijn van het segment in R zo verdeeld worden, dat BR anderhalf maal de rest RD is. Dan valt punt R tussen G en D {* volgens vorige} aangezien gesteld is dat G het zwaartepunt is in segment ABC. En daar de verhouding van het segment tot de ingeschreven driehoek dezelfde is als die van HD tot EG, zoals pas gezegd is; en de verhouding van HD tot EG kleiner is dan die van HD tot ER; daarom zal ook de verhouding van het segment tot de ingeschreven driehoek

⁴²) Eerst een herhaling van Theor. III, p. 123; dan voor de bovengrens een sterkere benadering dan die van Theor. IV, p. 127, want BR/RD is de limiet van BG/GD voor steeds kleinere bogen.
⁴³) Zie het eerste deel van het vorige theorema. ⁴⁴) Zie noot 25, p. 151.
⁴⁵) Zie Theorema VII van p. 305 van T. XI. ⁴⁶) Zie het 2e deel van het vorige theorema.

[ 169 ]

kleiner zijn dan die van HD tot ER, of dan die van HD vijfmaal genomen tot het vijfvoudige van ER. Nu is echter HD (daar hij gelijk is aan tweederde van DF) vijfmaal genomen gelijk aan tienderde, dat is drie-eenderde, maal DF. En ER, die ED bevat en tweevijfde van DB, zal als hij vijfmaal wordt genomen gelijk zijn aan tweemaal BD en vijfmaal ED; dat is aan tweemaal de hele EB en bovendien driemaal ED. Dus blijkt het segment ABC tot de ingeschreven driehoek een kleinere verhouding te hebben dan drie-eenderde maal DF tot tweemaal EB, dat is de middellijn BF, samen met driemaal ED. Wat te bewijzen was.

Theor. XVI. Propos. XIX.
Een willekeurige boog, kleiner dan de halve omtrek, is groter dan zijn koorde samen met eenderde van het verschil waarmee de koorde de sinus overtreft. En hij is kleiner dan de koorde samen met het lijnstuk dat zich verhoudt tot het genoemde eenderde, als viermaal de koorde samen met de sinus, tot tweemaal de koorde met driemaal de sinus⁴⁷)

Gegeven een cirkel met middelpunt D en middellijn FB. En boog BA moet kleiner zijn dan de halve omtrek, waarbij de koorde BA wordt getrokken, en ook de sinus AM, te weten degene die loodrecht staat op middellijn FB. Laat verder gelijk zijn aan deze AM de rechte GH, en GI gelijk aan de koorde AB. Het overschot is dus HI, en eenderde deel IK daarvan wordt aan GI toegevoegd. Aangetoond moet worden ten eerste, dat boog AB groter is dan de hele GK. Doch dit is duidelijk uit Theorema 7⁴⁸).
Maar wanneer bij die GI wordt opgeteld IO, die tot het derde deel IK van HI een verhouding heeft van viermaal GI samen met GH, tot het dubbele van GI met het drievoudige van GH; dan zeg ik dat de hele GO groter is dan boog AB.
Laat namelijk op de lijnen GH, HI en IO driehoeken worden opgericht, waarvan de gemeenschappelijke top L is, en de hoogte gelijk aan de straal DB.

⁴⁷) Het eerste deel is identiek met Theor. V, p. 129. [... Er volgen formules bij het 2e deel.]
⁴⁸) Zie de laatste alinea van het bewijs van Theor. VII, p. 135.

[ 171 ]

En laat worden verbonden DA, en getrokken de middellijn CE van de cirkel, die de rechte AB doormidden deelt in N, en de boog AB in E. En laat verbondenworden AE en EB.

Aangezien dan OI tot IK is als viermaal GI samen met GH, tot tweemaal GI met driemaal GH, zal gelden, als van elke volgende het drievoudige wordt genomen: OI tot IH (deze is immers driemaal IK), als viermaal GI samen met GH tot zesmaal GI met negenmaal GH. En door samenstellen: OH tot HI, als tienmaal elk van beide IG en GH tot zesmaal IG met negenmaal GH; of als van deze eenderde deel wordt genomen: als tienderde maal de twee GI en GH samen, tot tweemaal GI met driemaal GH.
Nu is de verhouding van GI tot GH, dat is die van BA tot AM, dezelfde als die van BD tot DN, wegens de gelijkvormige driehoeken BAM en BDN. Dus is OH tot HI ook als ¹⁰/₃ van beide BD en DN samen tot tweemaal BD met driemaal DN, dat is als ¹⁰/₃ NC tot middellijn EC met driemaal DN. Doch kleiner dan deze verhouding is de verhouding van segment AEB tot driehoek AEB {* volgens vorige}. Dus van genoemd segment tot genoemde driehoek is de verhouding kleiner dan van OH tot HI, dat is dan van driehoek OHL tot driehoek IHL. En driehoek IHL is gelijk aan driehoek AEB. Wat als volgt wordt aangetoond.
Driehoek GHL is immers gelijk aan driehoek DAB, aangezien ze basis en hoogte andersom gelijk hebben. En met een dergelijke redenering, aangezien GI gelijk is aan de rechte AB, zal driehoek GIL gelijk zijn aan de twee driehoeken DAE en DBE samen, dat is aan vierhoek DAEB. Dus is het noodzakelijk dat driehoek HIL gelijk is aan driehoek AEB, wat we zeiden.
Dus zal segment AEB tot zijn ingeschreven driehoek AEB ook een kleinere verhouding hebben dan driehoek OHL tot dezelfde driehoek AEB. Derhalve zal driehoek OHL groter zijn dan segment AEB. En daarom de hele driehoek OGL groter dan de sector DAEB. En de hoogte van driehoek GLO is gelijk aan de straal DB. Dus zal de basis GO groter zijn dan boog AB. Wat te bewijzen was.

Hieruit is verder duidelijk dat over de hele omtrek ook kan worden uitgesproken dat, Als bij een cirkel worden ingeschreven twee gelijkzijdige veelhoeken, waarvan de ene het dubbele aantal zijden heeft van de andere, en als aan eenderde van het verschil van de omtrekken wordt toegevoegd de omtrek van de grootste veelhoek, dan zal het samengestelde hiervan kleiner zijn dan de omtrek van de cirkel. En als bij dezelfde grootste omtrek een lijn wordt opgeteld die zich verhoudt tot het genoemde eenderde van het verschil, als viermaal de grootste omtrek samen met de kleinste omtrek, tot tweemaal de grootste met driemaal de kleinste, zal het samengestelde de omtrek van de cirkel overtreffen.⁴⁹)

⁴⁹) Zie de tweede formule van noot 47 [de eerste van n. 47 op p. 169].

[ 173 ] [ 1654, 40 ]

Problema IV. Propos. XX.
De verhouding van de omtrek tot de middellijn te onderzoeken; en uit gegeven koorden, in een gegeven cirkel ingeschreven, te vinden de lengte van de bogen waaronder deze zich uitstrekken.

Gegeven een cirkel met middelpunt D, waarvan CB een middellijn is, en een boog BA die een zesde deel van de omtrek is, waarbij de koorde AB wordt getrokken, evenals de sinus AM.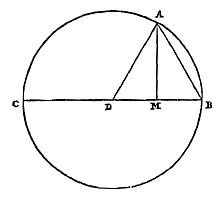
Als dan gesteld wordt dat de halve middellijn DB van 100000 delen is, zal de koorde BA ook van zoveel delen zijn. En AM van 86603 delen en niet één minder (dat wil zeggen, als een deel of eenheid wordt afgetrokken van 86603 zal het minder worden dan het benodigde)⁵⁰), als zijnde de helft van de zijde van een in de cirkel ingeschreven gelijkzijdige driehoek.

Dientengevolge wordt het overschot van AB boven AM 13397, kleiner dan het ware. Als hiervan het derde deel 4465²/₃ wordt opgeteld bij AB van 100000, komen er 104465²/₃ delen, kleiner dan boog AB. En dit is de eerste ondergrens, waarbij we hierna een andere zullen vinden die dichterbij de ware is. Doch eerst moet er ook een bovengrens gezocht worden volgens het voorgaande Theorema.

Er zijn namelijk drie getallen waarbij een vierde evenredige moet worden gezocht. Het eerste is het aantal delen van tweemaal AB en driemaal AM, dat 459807 zal zijn, kleiner dan het ware (want er moet ook op gelet worden dat het kleiner is, en evenzo bij de volgende zoals gezegd zal worden), het tweede van viermaal AB en eenmaal AM, dat is 486603, groter dan het ware. En het derde driemaal het overschot van AB boven AM, 4466, groter dan het ware. Dus de vierde evenredige zal zijn 4727, groter dan het ware, en als het opgeteld wordt bij AB van 100000 komt er 104727, groter dan het aantal delen dat boog AB bevat, een zesde deel van de omtrek {* volgens het vorige}. Dan hebben we nu de lengte van boog AB gevonden volgens een ondergrens en een bovengrens, waarvan de laatste zeker veel dichterbij de ware is, daar de beste benadering van de ware 104719 is [<].

Maar uit deze beide zal een andere ondergrens worden verkregen, nauwkeuriger dan de vorige, als we het volgende voorschrift gebruiken, dat afhangt van een zorgvuldiger beschouwing van zwaartepunten⁵¹).

⁵⁰) De zin tussen haakjes is door Huygens toegevoegd in de marge van het exemplaar dat we bezitten.
⁵¹) De handschriften en brieven geven geen uitsluitsel over de manier waarop de regel die volgt is gevonden. We weten alleen uit brief No. 185 van 1 april 1654 (p. 279 van T. I) dat een parabool gebruikt is, zoals bij het 2e deel van Theorema XVI. [... Er volgt een mogelijke manier.]

[ 175 ]

Vierderde van het verschil van de gevonden grenzen moet worden toegevoegd aan tweemaal de koorde en driemaal de sinus, en de verhouding die het hieruit samengestelde heeft tot drie-eenderde of 10/3 van de sinus en de koorde samen, dezelfde verhouding moet het overschot hebben van de koorde boven de sinus tot een andere. Deze laatste bij de sinus opgeteld geeft een rechte die kleiner is dan de boog.⁵²)

⁵²) [... Bewijs met formules.]

[ 177 ]

De ondergrens was 104465²/₃, de bovengrens 104727; het verschil hiervan is 261¹/₃. En weer moet bij drie getallen de vierde evenredige worden gevonden. Het eerste is van het aantal delen van tweemaal AB en driemaal AM en vierderde van het verschil van de grenzen, 460158, groter dan het ware. Het tweede ¹⁰/₃ van AB en AM samen, 622008, kleiner dan het ware. Het derde tenslotte is het overschot van AB boven AM, 13397 kleiner dan het ware. Daarbij is de vierde evenredige 18109, kleiner dan het ware. Dit dus, opgeteld bij het aantal delen van AM 86602½, kleiner dan het ware, maakt 104711½, kleiner dan boog AB.
Daarom zal het zesvoudige ervan 628269 kleiner zijn dan de hele omtrek. Maar aangezien 104727 groter is gevonden dan boog AB, zal het zesvoudige daarvan 628362 groter dan de omtrek zijn. Dus de verhouding tussen de omtrek en de middellijn is kleiner dan 628362, doch groter dan 628269 tot 200000. Of kleiner dan 314181, doch groter dan 314135 tot 100000. Waardoor vaststaat dat deze in elk geval kleiner is dan drie-eenzevende, en groter dan 3¹⁰/₇₁. En ook wordt hierdoor weerlegd de fout van Longomontanus⁵³), die heeft geschreven dat de omtrek groter is dan 314182⁵⁴) delen waarvan de straal er 100000 heeft.

Laat nu de boog AB ¹/₈ van de omtrek zijn, en AM, de helft van de zijde van een in de cirkel ingeschreven vierkant, zal van 7071068 delen zijn, en niet één kleiner, waarvan de straal DB er 10000000 heeft. En AB, de zijde van een achthoek, van 7653668, niet één groter. Met deze gegevens zal overeenkomstig het voorgaande als eerste ondergrens voor de lengte van boog AB gevonden worden 7847868. Daarna als bovengrens 7854066. En uit beide weer als nauwkeuriger ondergrens 7853885. Waardoor vaststaat dat de omtrek tot de middellijn een kleinere verhouding heeft dan van 31416¹/₃, doch groter dan 31415 tot 10000.

En daar de bovengrens 7854066 minder van de ware lengte van boog AB verschilt dan 85 delen (boog AB is immers, volgens wat we hierboven hebben aangetoond⁵⁵) groter dan 7853981); en daar 85 delen minder dan twee boogseconden uitmaken, dat wil zeggen 2/1296000 van de omtrek, want de hele omtrek heeft er meer dan 60000000; is hieruit duidelijk: als we van een rechthoekige driehoek de hoeken zoeken uit de gegeven zijden, op de manier van die bovengrens kort hiervoor, zullen we nooit twee

⁵³) Zie over hem en zijn werk van 1644 [p. 73-74: Pell] over de kwadratuur van de cirkel T. I, p. 176, noten 4 en 5. Al in Cyclometria ex lunulis ... (1612), p. 55 geeft hij 3,14185959.. In 1644, p. 24 [en 1634, p. 103]: 3,14185960..
⁵⁴) In het exemplaar dat we bezitten is het laatste cijfer met pen veranderd, waarschijnlijk door Huygens. Er staat 314185.
⁵⁵) Laatste alinea van Problema I, Prop. X, p. 143: omtrek groter dan 62831852, een achtste ervan is groter dan 7853981.

[ 179 ]

seconden afwijken; ook al zouden de zijden om de rechte hoek aan elkaar gelijk zijn, zoals ze hier waren in driehoek DAM.

Als echter de verhouding van zijde DM tot MA zodanig is, dat hoek ADM niet ¼ van de rechte overtreft, zal de fout niet een zestigste van een seconde zijn. Als immers boog AB gesteld wordt op 1/16 van de omtrek, zal AM, de helft van de zijde van een in de cirkel ingeschreven gelijkzijdige achthoek, zijn van 382683433 delen, niet één kleiner. En AB, de zijde van een zestienhoek, 390180644 en niet één groter, waarvan de straal DB er 1000000000 heeft. Dientengevolge wordt de eerste ondergrens voor de lengte van boog AB bevonden van 392679714 delen. De bovengrens van 392699148. En hieruit weer de ondergrens 392699010. Nu staat vast uit het boven bewezene⁵⁶) dat boog AB, 1/16 van de omtrek, groter is dan 392699081, wat de bovengrens te boven gaat met 67 delen. Deze dan maken minder uit dan een zestigste seconde, dat wil zeggen 1/77760000 van de hele omtrek, aangezien deze in elk geval groter is dan 6000000000.

Verder zal uit de nieuwste gevonden grenzen een verhouding van omtrek tot middellijn te voorschijn komen die kleiner is dan 3141593¹/₅, doch groter dan 3141592 tot 1000000.

Maar als boog AB wordt gesteld op 1/60 van de omtrek, of van 6 delen waarvan de hele er 360 heeft; dan zal AM, de helft van de zijde van een (ingeschreven)⁵⁷) dertighoek, zijn van 10452846326766 delen, niet één kleiner, waarvan de straal er 100000000000000 heeft. En AB, zijde van een (ingeschreven)⁵⁷) zestighoek, van 10467191248588, niet één groter. En hieruit zal boog AB gevonden worden volgens de eerste ondergrens 10471972889195. Volgens de bovengrens 10471975512584. En hieruit de andere ondergrens 10471975511302. Dientengevolge wordt de verhouding van omtrek tot middellijn kleiner dan 31415926538, doch groter dan 31415926533 tot 10000000000.

Als deze grenzen gezocht zouden moeten worden door optelling van de zijden van ingeschreven en omgeschreven veelhoeken, zou het neerkomen op bijna vierhonderd duizend zijden⁵⁸). Want uit een ingeschreven en omgeschreven zestighoek zou alleen bewezen worden, dat de verhouding van omtrek tot cirkel kleiner is dan 3145 tot 1000, doch groter dan 3140. Zodat het aantal ware tekens, dat door onze redenering blijkt te zijn voortgebracht, het drievoudige is en meer. En als iemand het bij veelhoeken nog verder probeert, zal hij merken dat hetzelfde altijd uitkomt; om een reden die ons niet onbekend is, maar die een vrij lange uitleg zou vereisen⁵⁹).

Doch verder meen ik dat het voldoende duidelijk is hoe, gegeven willekeurige andere gegeven ingeschreven veelhoeken, hiermee de lengte kan worden gevonden van de bogen waaronder ze liggen. Als ze immers groter zijn dan de zijde van een ingeschreven vierkant, moet de lengte van de op de halve omtrek

⁵⁶) Zie nog steeds de plaats van de vorige noot.
⁵⁷) De woorden tussen haakjes werden in de marge toegevoegd door Huygens in het exemplaar dat we bezitten.
⁵⁸) Met de formules van n. 7, p. 94: 240000 zijden. [Vgl. brief No. 181, aan van Schooten, maart 1654.]
⁵⁹) Zie noot 15, p. 142.

[ 181 ]

resterende boog gezocht worden, waarvan dan ook de koorde gegeven wordt. En te weten is dat ook de koorden van halve bogen gevonden worden, wanneer de koorde van de hele boog gegeven is. En als we op deze manier tweedelingen willen gebruiken, zullen we zonder moeite bij elke koorde de lengte van de boog ervan te weten kunnen komen, zo dichtbij de ware als we willen. Dit is nuttig voor het onderzoeken van sinus-tabellen. Ja ook om ze samen te stellen; omdat als van een boog de koorde bekend is, ook die van een iets grotere of kleinere voldoende nauwkeurig kan worden bepaald.

[ 183 ] [ 1654, 45 ]

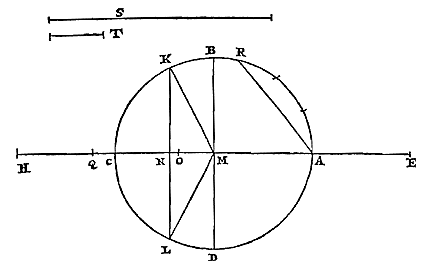
Christiaan Huygens, C.z.

Constructies van enige beroemde problemen.

Probl. I.

Een gegeven bol met een vlak zo te verdelen, dat de segmenten tot elkaar een gegeven verhouding hebben.¹)
Archimedes heeft dit probleem ontward in boek 2 van 'Over de bol en de cilinder'²). Doch het schijnt dat hij de beloofde constructie niet heeft uitgelegd, tenzij het die is welke Eutocius in een of ander oud boek heeft gevonden en in zijn commentaren ingelast³). Deze wordt echter uitgevoerd door snijding van een parabool en een hyperbool, zoals ook die waarvan Dionysodorus de bedenker is⁴), die evenwel verschilt van de vorige. Behalve deze twee voert Eutocius⁵) ook een derde aan uit een boek van Diocles over brandspiegels, die een beschrijving van een hyperbool en een ellips vereist. Doch de onze die we hier zullen beschrijven verlangt de driedeling van een hoek; en deze manier van construeren lijkt bij problemen over lichamen in zekere zin de eenvoudigste, en het meest geschikt voor gebruik.

Laat dus gegeven zijn een bol met middelpunt M en middellijn CA. En gegeven zij de verhouding van een lijn S tot T, van een grotere tot een kleinere. We stellen ons voor dat de bol wordt gesneden met een vlak langs middellijn AC, en dat de cirkel CBAD daarin de grootste is. En laat middellijn CA aan weerskanten verlengd worden, en aan de halve middellijn gelijk gesteld elk van deze twee CH en AE. En laat de hele HE in Q zo worden verdeeld, dat EQ tot QH is als S tot T.

¹) Zie het Voorbericht (p. 102) over de historie van dit probleem. De oplossing die volgt staat in iets andere vorm op p. 16-18, datum 31 jan. 1652. [Eerder: p. 9, aan Gregorius (24 jan. 1652), T. I, No. 119.]
²) Zie p. 3, n. 3. [Heiberg, I, 210; ed. Basel, Comm. p. 45-47; Engl.: Heath, p. 62.]
³) Zie p. 12, n. 16 en 17. [Ed. Basel 1544, p. 32-37; Engl.]
⁴) Ed. Basel p. 37-38 (Heiberg III, p. 189). [Engl. Vgl. Gregorius in T. I, 137, 18 febr. 1652.]
⁵) Ed. Basel, p. 38-42 (Heiberg III, p. 189). [Engl.]

[ 185 ]

Verder wordt aan MQ gelijk gesteld de rechte AR bij de omtrek. En aan die welke onder een derde deel van de boog AR ligt wordt gelijk genomen MN. En door punt N wordt een vlak KL getrokken dat loodrecht staat op middellijn CA. Ik zeg dat dit de bol zo snijdt, dat het segment waarvan A de top is tot dat waarvan de top C is, een verhouding heeft als van S tot T⁶).

Immers: laat de bol door middelpunt M worden gesneden met het vlak BD evenwijdig aan KL, en laat verbonden worden KM en ML; en we stellen ons een kegel voor met als basis de cirkel gemaakt door de snede KL, en M als top. En zoals het kwadraat van CM is tot het kwadraat van MN, zo moet MN tot NO zijn in lengte. Dan zal door omzetting van de verhouding gelden: zoals het kwadraat van CM, of het kwadr. van KM, is tot het kwadraat van KN (kwadr. KN is immers het overschot van kwadraat KM boven kwadr. MN), zo is lijn NM tot MO.
Zoals nu kwadr. KM, dat is kwadr. BM is tot kwadr. KN, zo is de cirkel om middellijn BD tot die om middellijn KL. Dus zal ook de eerste cirkel zich tot de tweede verhouden als NM tot MO. En derhalve zal kegel KML gelijk zijn aan de kegel met als basis de cirkel om middellijn BD, en als hoogte MO {* 15.12 Elem.⁷)}. Nu heeft deze kegel tot de halve bol BCD, dat is tot de kegel met als basis dezelfde cirkel om middellijn BD, en hoogte MH {* 32.1 [34] Archim. de Sphaer. & Cylin.⁸)}, een verhouding als van MO tot MH. Dus ook de kegel KML zal tot de halve bol BCD zijn zoals MO tot MH. En andersom.

Verder nu, aangezien de halve bol BCD tot de bolsector MKCL is als het bolvormige oppervlak van de eerste tot dat van de laatste {* 42.1 [44] Archim. de Sphaer. & Cyl.⁹)}, dat is als MC tot CN {* 3.2 Archim. de Sphaer. & Cyl.¹⁰)}; zal door omzetting van de verhouding de halve bol BCD zijn tot het deel ervan dat overblijft als sector MKCL wordt weggenomen, zoals CM tot MN; of als van deze twee het dubbele wordt genomen, als HM tot OQ. Dat namelijk OQ het dubbele is van MN zullen we later aantonen.
En aangetoond is, dat de halve bol BCD tot kegel KML is zoals HM tot MO. Dus nu zal gelden: de halve bol BCD is tot het hele segment tussen de vlakken BD en KL bevat, als HM tot QO en OM samen {* 24.5 Elem.¹¹)}, dat is tot MQ. Daarom zal ook door omzetting van de verhouding de halve bol BCD tot segment KCL zijn als MH tot HQ.

⁶) Een iets andere constructie is op 9 aug. 1653 [T. I, p. 239] meegedeeld aan Kinner von Löwenthurn, lijkend op die van 31 jan. 1652 (zie n. 1). Zie n. 4 op p. 16. Koorde AR = (S – T) / (S + T) × AC.
⁷) Zie noot 10 op p. 11. [Clavius (1607) p. 480.]
⁸) Zie noot 7 op p. 17. [Ed. Basel, p. 32; Heiberg I, p. 141 (nr. 34).]
⁹) Zie noot 11 op p. 11. [Ed. Basel, p. 40; Heiberg I, p. 181.]
¹⁰) Zie noot 9 op p. 17. [Ed. Basel, p. 45; Heiberg I, p. 207.]
¹¹) Zie noot 28, p. 312 van T. XI en n. 13 op p. 12 en 13. [Clavius, p. 516.]

[ 187 ]

En van de voorafgaande het dubbele genomen: de hele bol tot segment KCL als EH tot HQ. En door verdeling, segment KAL tot segment KCL als EQ tot QH, dat is als S tot T. Wat gedaan moest worden.
Wat nu is gezegd, dat OQ het dubbele is van MN, zal als volgt duidelijk worden. Omdat immers geldt: zoals het kwadraat van CM is tot het kwadr. van MN, zo is MN tot NO in lengte; en QM is gelijk aan de koorde van boog AR, waarvan een derde deel de koorde MN heeft; daarom zullen de twee QM en NO samen gelijk zijn aan driemaal MN, zoals door de volgende hulpstelling wordt bewezen. En om deze reden, als de gemeenschappelijke ON eraf wordt gehaald, zal alleen QM gelijk zijn aan tweemaal NM en MO. Maar dezelfde QM is gelijk aan deze twee QO en OM samen, dus blijkt het dubbele van MN gelijk te zijn aan OQ.

Hulpstelling.
Als een omtreksboog in drie gelijke delen wordt gesneden, zijn de drie rechten samen, die koorde zijn van de gelijke delen, gelijk aan de koorde van de hele boog en die rechte, die zich tot de koorde van eenderde deel verhoudt als het kwadraat hiervan tot het kwadraat van de halve middellijn.
Laat de boog van sector ABC in drie gelijke delen worden verdeeld door de punten D en E. En eronder liggen als koorde de rechten BD, DE en EC; en onder de hele boog de lijn BC. Verder worden getrokken DA en EA, en ze zullen de koorde BC snijden in de punten G en H. Laat HF evenwijdig zijn met GD.

Aangezien dan de omtrek BDE het dubbele is van omtrek EC, en de hoek EAC die op de laatste staat wordt bij het middelpunt gevormd, terwijl hoek BCE die op de eerste staat bij de omtrek wordt gevormd; daarom zal hoek BCE, dat is hoek HCE in driehoek HCE gelijk zijn aan hoek CAE in driehoek CAE. Maar de hoek bij E is aan beide gemeenschappelijk; dus de genoemde driehoeken zijn gelijkvormig met elkaar. En dan geldt: zoals AE tot EC is, zo is EC tot EH. Dus de verhouding van AE tot EH, dat is van DE tot EF, is de kwadratische verhouding van die van AE tot EC, en derhalve dezelfde als die van het kwadraat van AE tot het kwadr. van EC of kwadr. van ED. Dan zal andersom FE tot ED zijn zoals kwadr. ED tot kwadr. EA. Daarom moet worden aangetoond, dat de drie BD, DE en EC samen gelijk zijn aan de koorde BC en EF. Wat zeker duidelijk is; want CE is gelijk aan CH; BD is gelijk aan BG; en DE aan GH en FE samen. Dus staat het voorgestelde vast.

[ 189 ]

Nu hebben we de boog BC kleiner genomen dan de halve omtrek, aangezien hij bij de constructie van het probleem altijd zo wordt gevonden. De hulpstelling heeft wel betrekking op willekeurige bogen, en het bewijs is weinig anders bij bogen die groter zijn dan de halve omtrek¹²).

¹²) Deze opmerking ontbreekt in de weergave van 31 jan. 1652 (p. 16-18), het lemma staat er wel.

Probl. II.

Een kubus te vinden die tweemaal zo groot is als een gegeven kubus.¹³)
Hiertoe zullen we eerst een onvolmaakte constructie voorstellen die nuttig is voor mechanische toepassing; daarna zullen we er een nauwkeurige aan toevoegen, die evenwel alleen vervolmaakt kan worden door vaker de proef te nemen. En inderdaad vereisen alle ruimtelijke problemen hetzij deze¹⁴), hetzij een beschrijving van kegelsneden.

Laat dus gegeven zijn een kubus met zijde AB, en te vinden is de zijde van de dubbele kubus.

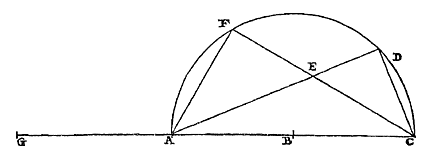
Met straal BA wordt een halve cirkel AFC beschreven. En boog AF is een derde deel van de halve cirkel, CD een vierde; en getrokken worden CF en AD, waarvan het snijpunt is in punt E. AE zal de zijde van de gevraagde kubus zijn, die echter overtreffend met iets gerings, dat kleiner is dan 1/2000 deel ervan, zoals gemakkelijk met getallen kan worden onderzocht.
AE is namelijk de secans van een hoek van 37° 30', die derhalve groter is dan 12600 delen waarvan AF of AB er 10000 heeft. Doch kleiner dan 12605. Dus daar een kubus op 12600 groter is dan het dubbele van die op AB van 10000, zal ook de kubus op AE groter zijn dan het dubbele van de kubus op AB. Aan de andere kant, omdat AE groter is dan 12600 delen zal 1/2000 AE groter zijn dan 6 delen. De hele AE is echter kleiner dan 12605. Dus door van AE een tweeduizendste deel ervan af te halen zal de rest kleiner zijn dan 12599; zoveel blijven er immers over wanneer van 12605 wordt afgetrokken 6. Maar nu is een kubus op 12599 kleiner dan het dubbele van de kubus op 10000. Dus zal AE, verkleind met een tweeduizendste deel ervan, ook zeker een kleinere kubus voortbrengen dan het dubbele van de kubus met zijde AB.

Verder, voor een volmaakte constructie moet wel CF getrokken worden zoals hiervoor; AD echter zo, dat de koorde CD gelijk is aan de afgesneden EF. En inderdaad zeg ik met dit gestelde dat de kubus op AE het dubbele is van die op AB.

Immers: als CA wordt verlengd, en AG gelijk is aan AE, dan is wegens gelijkvormige driehoeken EC tot CD, dat is EF, als EA tot AF, dat is als GA tot AB.

¹³) Vgl. p. 45-48 (1-2 maart 1652): exacte oplossing, en benaderde met langer bewijs.
¹⁴) In het exemplaar dat we bezitten is 'isthic' door Huygens met pen veranderd in 'hoc'.

[ 191 ]

En door samenstelling: CF tot FE als GB tot BA of AF. En door verwisseling: CF tot GB als EF tot FA. En daarom: zoals het kwadraat van CF is tot het kwadr. van GB, zo is kwadr. EF tot kwadr. FA. En door samenstelling: zoals kwadr. CF en GB tot kwadr. GB, zo is kwadr. EF en FA samen, dat is kwadr. EA, tot kwadr. AF. Nu is kwadr. CF en GB samen gelijk aan rechthoek GCA met kwadr. AG, wat wordt aangetoond als volgt.

Het kwadraat van GB is namelijk gelijk aan rechthoek CGA en kwadraat AB of AF {* 6.2 Elem..¹⁵)}. En daarom, als aan beide kanten wordt opgeteld kwadraat FC, zullen de kwadraten GB en FC samen gelijk zijn aan rechthoek CGA en kwadraat AC. Nu is rechthoek CGA met kwadraat AC gelijk aan rechthoek GCA met kwadraat GA. Dus zijn ook de kwadraten CF en GB samen gelijk aan rechthoek GCA met kwadraat AG, zoals we hebben gezegd.
Zoals dus rechthoek GCA met kwadraat AG tot kwadr. GB is, zo is kwadr. EA tot kwadr. AF, dat wil zeggen: zo is kwadraat GA tot kwadr. AB. En door verwisseling: zoals rechthoek GCA met kwadraat GA tot kwadraat GA is, zo is kwadr. GB tot kwadr. AB. Door dan te verdelen zal gelden: zoals rechthoek GCA tot kwadr. GA is, zo is kwadr. GB met kwadraat AB eraf genomen, dat is rechthoek CGA, tot kwadr. AB. En door weer te verwisselen: zoals rechth. GCA tot rechth. CGA, dat is zoals CA tot AG, zo is kwadraat GA tot kwadr. AB. Daarom zal wat ontstaat uit kwadraat GA maal GA, dat is kubus GA gelijk zijn aan wat ontstaat uit kwadraat AB maal AC, dat is aan het dubbele van de kubus op AB. Wat te bewijzen was¹⁶).

¹⁵) Zie p. 46, noot 2. [Clavius p. 178.] ¹⁶) Zie nog p. 46, n. 3 [eenvoudiger methode].

Probl. III.

Bij twee gegeven rechten twee middelevenredigen te vinden.¹⁷)
Verscheidene constructies van oude Meetkundigen voor dit Probleem zijn meegedeeld door Eutocius bij boek 2 van Archimedes over de Bol en de Cilinder¹⁸), maar niet allemaal van verschillende vinding, zoals hij ook zelf terecht opmerkt. De vinding van Hero¹⁹) schijnt te zijn gevolgd door Apollonius en Philo Byzantinus²⁰), hoewel sommigen menen dat Hero van later tijd was dan Apollonius²¹). De manier van Diocles door Pappus en Sporus²²).

¹⁷) Zie voor de historie van dit probleem p. 103-106 van het Voorbericht.
¹⁸) Ed. Basel, Comm. p. 14-27 (Heiberg III, p. 66-127).
¹⁹) Ed. Basel, p. 15; zie ook p. 40 n. 10 [Pappus, Math. Coll., 1588, p. 6r en 6v]. [Figuur rechts: ms Willem van Moerbeke (ca. 1270) bij Vaticaan.]
²⁰) Ed. Basel, p. 16. Eutocius zegt al dat de 3 constructies bijna gelijk zijn.
²¹) Deze vraag heeft velen bezig gehouden. Cantor, Vorlesungen (1894), p. 347 plaatst Hero in de 1e eeuw n. Chr., 2 eeuwen na Apollonius.
²²) Ed. Basel, p. 17-20. Diocles gebruikt zijn cissoïde. [...]

[ 193 ]

Doch de constructie van Nicomedes²³) op dezelfde plaats²⁴), is subtiel in vergelijking met de overige, en Fr. Vieta heeft die in iets andere vorm opgenomen in zijn Supplementum geometriae²⁵). Die van R. Descartes is uitstekend en nieuw, door snijding van een parabool en een omtrek²⁶), waarvan het bewijs is te lezen in de boeken over Harmonieën van M. Mersenne²⁷). En van ons zijn de volgende.

²³) Zie p. 13, n. 2 en p. 15 [Pappus 1588, p. 5v en 56v]. Zie ook p. 4-6: Nicomedes inspireerde Huygens. [...]
²⁴) Ed. Basel p. 26-27.
²⁵) Zie Prop. V in Opera mathematica, 1646, p. 242 [p. 14r en 14v in ed. 1593]. [... Bespreking.]
²⁶) La Geometrie (1637), p. 395-396: 'L'invention de deux moyenes proportionelles'.
²⁷) Harmonicorum Libri, 1636, II, 147-148 [over de toonladder: elf middelevenredigen in een octaaf; p. 146: "vir summus", het bewijs is van Roberval].

Laat de grootste van de gegeven lijnen zijn AC²⁸), die doormidden wordt gesneden in E. De kleinste is AB, die zo wordt opgesteld dat de driehoek EAB gelijke benen AE en EB heeft. En parallelogram CABD wordt voltooid. En AC en AB worden verlengd. Verder wordt tegen D een liniaal gezet, en deze wordt bewogen tot waar hij de stand GF heeft, namelijk zo, dat hij de rechte EF gelijk aan de rechte EG afsnijdt (dit nu bereiken we of door vaker te proberen, of door het beschrijven van een hyperbool, zoals later zal worden getoond). Ik zeg dat tussen AC en AB de twee middelevenredigen BG en CF gevonden zijn.

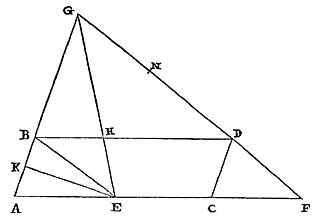
Laat namelijk EK loodrecht op AB staan. Omdat BE dus gelijk is aan EA, zal AB in K doormidden gedeeld worden; doch de lijn BG is erbij gevoegd. Dus de rechthoek AGB met het kwadraat van KB zal gelijk zijn aan kwadraat KG [^]. En als aan elk van beide wordt toegevoegd kwadraat KE, zal rechthoek AGB samen met de kwadraten BK en KE, dat is samen met kwadraat BE, gelijk zijn aan kwadraat EG. Evenzo, omdat AC doormidden gedeeld wordt in E, en de lijn CF erbij is gevoegd, zal rechthoek AFC met kwadraat EC gelijk zijn aan kwadraat EF.
Nu is kwadraat EF gelijk aan kwadraat EG. Dan zal rechthoek AFC met kwadraat CE gelijk zijn aan rechthoek AGB met kwadraat BE. Maar nu is kwadraat CE of EA gelijk aan kwadraat EB. Dus is ook de rest rechthoek AFC gelijk aan rechthoek AGB. En daarom geldt: zoals FA tot AG is, zo is BG tot CF. Doch zoals FA tot AG is, zo is DB tot BG, en zo is ook FC tot CD.

²⁸) Zie p. 49-51, m.n. noot 5: 9-10 maart 1652. [...]

[ 195 ]

Dus zoals DB, dat is AC, tot BG is, zo is BG tot FC, en FC tot CD, dat is AB. Wat te bewijzen was.
Wat nu gezegd is, dat ook door beschrijving met een hyperbool te vinden is hoe lijn FDG moet worden getrokken, zal vaststaan uit het volgende:
Laat het namelijk zo gedaan zijn dat EF en EG gelijk zijn, en laat GN gelijk aan DF genomen worden. Dus punt N ligt op een hyperbool die wordt beschreven door punt D om de asymptoten FA en AG {* 8.2 Conic.²⁹)}. Maar hetzelfde punt N ligt ook op een omtrek waarvan E het middelpunt is en ED de straal (dit is namelijk gemakkelijk te begrijpen omdat driehoek FEG gelijkbenig is, en NG gelijk aan DF). Dus het punt N is gegeven als snijpunt van de genoemde hyperbool en omtrek. Maar ook D is gegeven. Dus is de stand van lijn FG gegeven door hem te trekken door de punten N en D. En de samenstelling is duidelijk.

²⁹) Zie p. 46r van Apollonius, ed. Commandino (1566). [...]

Anders. ³⁰)
Een cirkel wordt beschreven om middellijn AC, gelijk aan de grootste van de gegeven lijnen, en geplaatst wordt AB, gelijk aan de kleinste daarvan, en parallelogram AD wordt voltooid; 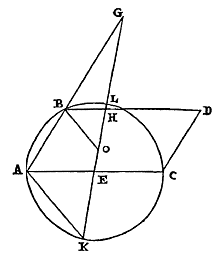en na verlenging van AB wordt uit het middelpunt E de rechte EHG getrokken op zo'n manier dat HD en HG aan elkaar gelijk zijn. Deze zal dan de omtrek snijden in L. Ik zeg dat bij de twee AC en AB de twee middelevenredigen BG en GL zijn gevonden.

Immers³¹): laat GE worden verlengd tot aan de omtrek in K, en AK verbonden, en daaraan evenwijdig BO. De driehoeken AEK en BHO zijn dus gelijkvormig; en omdat AE gelijk is aan EK, zullen ook BH en HO gelijk zijn. Maar ook HG en HD zijn aan elkaar gelijk. Dus is de hele OG gelijk aan BD, dat is aan middellijn AC of LK; en als de gemeenschappelijke LO wordt weggelaten, zullen overblijven de gelijke LG en OK. Nu is rechthoek KGL gelijk aan rechthoek AGB [^]. Dus zoals KG tot GA is, zo is BG tot GL. Maar zoals KG tot GA is, zo is OG tot GB en zo is de rest OK, dat is LG, tot BA. Dus zoals OG, dat is AC, tot GB is, zo is BG tot GL en GL tot AB. Wat te bewijzen was. Doch de vinding van deze constructie heeft dezelfde oorsprong als die van de voorgaande³²).

³⁰) Zie p. 52. ³¹) Zoals op p. 53, datum 5 juni 1652. [...] ³²) Zie p. 52, noot 9.

[ 197 ]

Anders. ³³)
Laat gegeven zijn AB en Q waarbij twee middelevenredigen gezocht moeten worden; met AB groter dan Q.

Laat AF gelijk worden genomen aan de helft van Q; en na verlenging van AB aan weerskanten, moet BR hieraan gelijk zijn. Laat nu op AB de loodlijn FC opgericht worden, en RC aan RA gelijk gesteld; en BC verbonden, en daaraan evenwijdig AE getrokken. Tenslotte wordt een liniaal tegen punt C gezet, en deze wordt bewogen tot waar hij de stand CD heeft en CE gelijk aan AD maakt. Ik zeg dat tussen AB en Q de twee middelevenredigen zijn CE en ED.

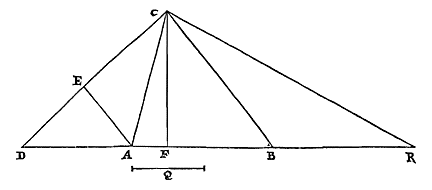
Immers: laat CA worden verbonden. Dan zal gelden, omdat RA en RC gelijk zijn en hoek CFA recht is: RA tot AC is als AC tot tweemaal AF, dat is Q; en derhalve is kwadraat AC gelijk aan de rechthoek op RA en Q. Nu is kwadraat AC met kwadraat AD en tweemaal rechthoek DAF, dat is die op DA en Q gevat, gelijk aan kwadraat DC {* 12.2 Elem.³⁴)}. Dus kwadraat DC zal gelijk zijn aan kwadraat DA samen met de rechthoeken op DA en Q, en op RA en Q, dat wil zeggen samen met de rechthoek op DR en Q.
Nu is kwadraat DB gelijk aan rechthoek RDA en kwadraat AB {* 6.2 Elem.³⁵)}. Dus zoals kwadraat DB tot kwadraat DC, dat is zoals kwadr. AB tot kwadr. AD (immers: zoals DB tot DC, zo is AB tot EC of AD) zo zal zijn rechthoek RDA met kwadraat AB tot de rechthoek op RD en Q, met kwadraat AD. Daarom is ook rechthoek RDA tot de rechthoek op RD en Q, zoals kwadr. AB tot kwadr, AD {* 19.5 Elem.³⁶)}.
Doch zoals kwadraat AB tot kwadraat AD is, zo is AB tot ED in lengte; want zoals BA tot AD is, zo is CE, dat is AD, tot ED. Dus rechthoek RDA is tot de rechthoek op RD en Q, dat is AD tot Q, zoals AB tot ED. En door verwisseling en omkering, BA tot AD zoals ED tot Q. Maar zoals BA is tot AD, dat is CE, zo is CE tot ED. Dus zoals AB tot CE is, zo is CE tot ED, en ED tot Q. Dus tussen AB en Q zijn middelevenredig CE en ED. Wat aangetoond moest worden.

³³) Vgl. p. 54-56, 16 en 19 maart 1652. [...] ³⁴) Zie noot 15 op p. 29 [Clavius, p. 192].
³⁵) Zie p. 46, noot 2 [Clavius, p. 178]. ³⁶) Zie noot 26, p. 311 van T. XI [Clavius, p. 510].

[ 199 ] [ 1654, 56 ]

Probl. IV.
Bij een gegeven vierkant, met een zijde verlengd, in de buitenhoek een rechte aanpassen van gegeven grootte, die gericht is naar de overstaande hoek.³⁷)

Laat er een vierkant BA zijn waarvan de zijde FA is verlengd. Gegeven is ook een lijn K. En er moet een rechte BDC worden getrokken, zodanig dat het afgesneden deel DC gelijk is aan de gegeven K.

Aan de kwadraten van K en EB wordt gelijk gesteld het kwadraat van EG; en op BG als middellijn wordt een halve cirkel BCG beschreven, die het verlengde van de rechte FA snijdt in C, en BDC wordt getrokken. Ik zeg dat DC gelijk is aan K. 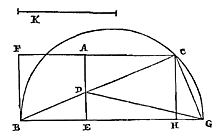Immers: laat CG en GD worden verbonden; en CH loodrecht op BG zijn. Omdat dan de driehoeken BED en CHG gelijkvormig zijn, en de zijden BE en CH bij de rechte hoeken aan elkaar gelijk, zal ook de zijde DB gelijk zijn aan zijde GC, en DE aan GH. Nu zijn de kwadraten DC en CG, dat is de kwadraten DC en CH en HG, gelijk aan kwadraat DG {* 47.1. Elem.³⁸)}, dat is aan de kwadraten GE en ED. Dus als van de laatste wordt afgenomen kwadraat ED, en van de eerste kwadraat HG, zullen de twee kwadraten DC en HC gelijk zijn aan kwadraat EG, dat is aan de kwadraten van K en EB {Door constructie}. En kwadraat EB is gelijk aan kwadraat CH. Dus ook zal het andere kwadraat DC gelijk zijn aan het kwadraat van K; en de rechte DC aan K zelf. Wat te bewijzen was.

Dit bewijs is verschillend van dat wat bij Pappus van Alexandrië is te lezen in boek 7, prop. 72³⁹). De constructie verschilt echter niet. Overigens hebben we gevonden dat op hetzelfde geval ook betrekking heeft het volgende.

³⁷) Historie van dit probleem: p. 106. [P. 19; brief aan van Schooten, 23 okt. 1653, in T. I, p. 247.]
³⁸) [...] Clavius, p. 147.
³⁹) Zie p. 206v van het werk [Math. Coll., 1588] aangehaald in noot 3 op p. 259 van T. II.

Probl. V.
Bij een gegeven vierkant met twee aangrenzende zijden verlengd, in de binnenhoek een rechte aanpassen van gegeven grootte, die door de overstaande hoek gaat. Deze mag echter niet kleiner zijn gegeven dan tweemaal de diagonaal van het vierkant.⁴⁰)

Gegeven een vierkant AB, en de zijden AF en AE zijn verlengd. Gegeven ook een lijn K, niet kleiner dan tweemaal de diagonaal van AB. En er moet door hoekpunt B een rechte DC aangelegd worden die gelijk is aan K.

⁴⁰) Historie van dit probleem: p. 107. [P. 19; brief aan van Schooten, 23 okt. 1653, in T. I, p. 247.]

[ 201 ]

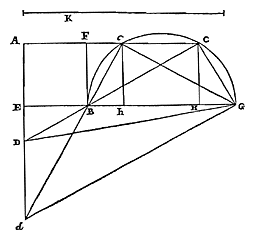Als K gelijk is aan tweemaal AB, is de constructie duidelijk; dan is immers door B een lijn te trekken die loodrecht staat op AB, en die zal aan het voorgestelde voldoen. Wanneer K echter groter is dan tweemaal AB, gaat de constructie volgens dezelfde woorden als in het voorgaande Probleem; en het bewijs is ook hetzelfde.

Dat nu de omtrek BCG het verlengde van AF zal snijden is duidelijk uit het volgende. Omdat immers K groter is dan tweemaal de diagonaal AB, zal het kwadraat van K groter zijn dan achtmaal het kwadraat van EB. Dus kwadraat EG is groter dan negenmaal het kwadraat van EB*); en derhalve is EG groter dan driemaal EB. De helft BG, dat is de straal van de beschreven halve cirkel, is dus groter dan EB of BF; dientengevolge is het noodzakelijk dat de rechte AC wordt gesneden door de omtrek BCG.

[ *) Gesteld was in Probl. IV: EG² = K² + EB².]

Probl. VI.
Bij een gegeven ruit met een zijde verlengd, in de buitenhoek een rechte aanpassen van gegeven grootte, die gericht is naar de overstaande hoek.⁴¹)

Gegeven de ruit AB, met de zijde FA verlengd. Verder is gegeven de lijn K. En de rechte BDC moet zo worden getrokken, dat het afgesneden deel DC gelijk is aan K.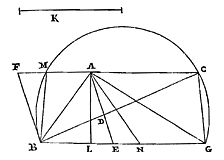

Laat de diagonaal AB getrokken worden, en de zijde BE verlengd; en aan de kwadraten van K en AB wordt gelijk gemaakt het kwadraat van AG. En op BG wordt een segment van een omtrek geplaatst dat een hoek inneemt die gelijk is aan hoek BFA. Dit zal het verlengde van zijde FA snijden, zoals straks aangetoond zal worden. Naar het snijpunt C dus wordt getrokken BC. Ik zeg dat het hiervan afgesneden deel DC gelijk is aan de gegeven lijn K.
Dat nu de beschreven omtrek het verlengde van zijde FA zal snijden, is als volgt aan te tonen. Laat getrokken worden AN zo, dat hoek BAN gelijk is aan hoek BFA of BEA. Driehoek BAN is dus gelijkvormig met driehoek BEA, en derhalve ook gelijkbenig. En daarom, als op BN een omtrek wordt beschreven die hoek BFA inneemt, zal deze de zijde FA raken in het punt A.

⁴¹) Historie van dit probleem: p. 107-108 [M. Ghetaldi, Apollonius redivivus, 1607, I, p. 17; P. Herigone, Cursus mathematicus, I (1634), 912-914]. Brief aan van Schooten, T. I, p. 247. Zie ook p. 26-31 (9 febr. 1652). [...]

[ 203 ]

Maar BG is groter dan BN; want kwadraat AG is groter dan kwadraat AN of AB, daar het gelijk is aan de kwadraten van K en AB. Daarom zal AG buiten de gelijkbenige driehoek BAN vallen. Dus is duidelijk dat een omtrek op BG beschreven, en die een hoek inneemt gelijk aan BFA of BAN, de lijn FAC snijdt. Laat het andere snijpunt M zijn en getrokken worden BM en GC, en uit A valt op BE de loodlijn AL.

Omdat dan kwadraat AG gelijk is aan de kwadraten van K en AB; en ook hetzelfde kwadraat gelijk aan de kwadraten AB en BG min tweemaal rechthoek GBL*), dat wil zeggen min rechthoek GBN; daarom zal K kwadraat gelijk zijn aan kwadraat BG min rechthoek GBN, dat is aan rechthoek BGN.
Nu geldt: zoals rechthoek BGN tot rechth. BE.GN is, zo is BG tot BE. Dus zoals BG tot BE, zo is ook kwadraat K tot rechthoek GN.BE, dat is rechthoek GBE min rechthoek NBE. En aan rechthoek GBE is gelijk rechth. CBD, aangezien GB tot BC is, zoals DB tot BE, wegens de gelijkvormige driehoeken GBC en DBE; ze hebben immers de hoek bij B gemeenschappelijk, en hoek BCG is gelijk aan BED. Evenzo is rechthoek NBE gelijk aan kwadraat AB omdat wegens gelijkvormige driehoeken geldt: zoals NB tot BA is, zo is AB tot BE. Dus zal GB tot BE zijn als kwadraat K tot rechthoek CBD min kwadraat AB.
Verder is aan rechthoek CBD min kwadr. AB gelijk rechthoek DA.AC; wat als volgt wordt aangetoond. Omdat namelijk de vierhoek CGBM in een cirkel ligt, zijn de hoeken CGB en BMC samen gelijk aan twee rechte hoeken. Maar ook de hoeken EDB en ADB. En hiervan is EDB gelijk aan hoek CGB wegens gelijkvormigheid van de driehoeken GBC en DBE. Dus zal hoek BMC ook gelijk zijn aan hoek ADB. Dan hebben de driehoeken ABM en ABD de hoeken M en D gelijk aan elkaar. Maar ook de hoeken bij A, en de zijde AB gemeenschappelijk. Dus zijn de genoemde driehoeken gelijkvormig en gelijk. En daarom is AM gelijk aan AD, en MB gelijk aan BD, en hoek MBA gelijk aan ABD. In driehoek MBC wordt hoek B dus in twee gelijke delen verdeeld door de rechte BA, en daarom is rechth. MBC min kwadraat BA gelijk aan rechthoek MAC [^]. Maar aan rechthoek CBM is gelijk rechthoek CBD; en aan rechthoek MAC is gelijk rechth. DAC. Dus rechth. CBD min kwadraat BA is gelijk aan rechthoek CAD, zoals gezegd is. Dus geldt: GB is tot BE zoals kwadr. K tot rechthoek DAC.
En zoals BG tot BE is, zo is rechth. GBE, dat is rechth. CBD, tot kwadraat BE. Dus zoals kwadraat K tot rechth. DAC is, zo is rechth. CBD tot kwadraat BE. Nu is de verhouding van rechthoek CBD tot kwadr. BE samengesteld uit de verhouding van DB tot BE, dat is DC tot CA, en uit de verhouding van CB tot BE of BF, dat is CD tot DA. Dus heeft ook kwadr. K tot rechth. DAC die verhouding die wordt samengesteld uit de verhouding van DC tot CA en DC tot DA, dat is die van kwadraat DC tot rechth. DAC. Daarom is kwadr. K gelijk aan kwadraat DC; en DC aan K in lengte. Wat te bewijzen was.

[ *) Omdat: AG² = AL² + LG² = AB² – BL² + LG² en: LG² = BG² – BL² – 2 BL.LG .]

[ 205 ]

Probl. VII.
Bij een gegeven ruit met twee aangrenzende zijden verlengd, in de binnenhoek een rechte aanpassen van gegeven grootte die door de overstaande hoek gaat. Deze mag echter niet kleiner zijn gegeven dan tweemaal de diagonaal die de overige twee hoekpunten van de ruit verbindt.⁴²)

Gegeven een ruit AB, met de zijden AF en AE verlengd; Verder is gegeven de rechte K waaraan gelijk gesteld moet worden CD, die door hoekpunt B gaat. Laat de diagonaal AB getrokken worden, en loodrecht daarop de lijn SBR, die zeker gelijk zal zijn aan tweemaal de diagonaal FE. Dan mag K niet kleiner zijn dan SR. Als hij echter gelijk is, is gedaan wat werd voorgesteld.

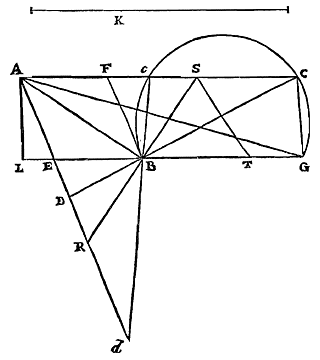
Maar laat gesteld worden dat K groter gegeven is dan SR. Nu zal in deze tekening de constructie, voorzover die is voorgesteld, dezelfde zijn als bij het voorgaande Probleem. Doch het bewijs is enigszins verschillend. Ten eerste namelijk wordt dit anders aangetoond, dat de omtrek op BG beschreven het verlengde van AF snijdt. Laat AL loodrecht staan op EB, en laat ST zo getrokken worden dat de hoek BST gelijk is aan de hoek EAF of BFS. Dus is driehoek BST gelijkvormig met driehoek BFS (want ze hebben ook de hoeken bij B gelijk), en derhalve is driehoek BST ook gelijkbenig.
De lijn AS blijkt dus gelijk te zijn aan LB met de helft van BT. Daarom zal tweemaal AS gelijk zijn aan tweemaal LB en de hele BT. Maar tweemaal AS is viermaal AF of EB. Dus viermaal EB is gelijk aan tweemaal LB en BT. En als de gemeenschappelijke hoogte BT wordt genomen, zal de rechthoek op viermaal EB en BT gelijk zijn aan tweemaal rechthoek LBT en kwadraat BT. En als aan beide kanten wordt bijgedaan kwadraat BL, zal rechthoek EBT viermaal met kwadraat LB gelijk zijn aan rechthoek LBT tweemaal met de kwadraten BT en BL, dat is kwadraat LT.
En omdat wegens gelijkvormige driehoeken TB tot BS is, zoals BS tot BF of BE, zal rechthoek EBT gelijk zijn aan kwadraat BS; en viermaal genomen aan kwadraat RS. Dus kwadr. SR met kwadraat LB is gelijk aan kwadraat LT. En kwadraat K (dat groter is dan kwadr. RS) samen met hetzelfde kwadraat LB is gelijk aan kwadraat LG, zoals uit de constructie duidelijk is, omdat namelijk kwadr. AG gelijk gesteld is aan de kwadraten van K en AB. Dus groter is kwadr. LG dan LT en LG groter dan LT, en BG dan BT.

⁴²) Historie van dit probleem: p. 109 [M. Ghetaldi, Apollonius redivivus, 1607, I, p. 19 en De resolutione et compositione mathematica (1630), p. 333; P. Herigone, Cursus mathematicus, I (1634), 913]. Brief aan van Schooten, T. I, p. 248. Zie ook p. 32-37 (11 febr. 1652). [...]

[ 207 ]

Daarom zal de omtrek op BG beschreven die hoek EAF inneemt, de rechte AS snijden; want als een dergelijke omtrek op BT wordt beschreven zal deze haar raken in punt S, aangezien hoek BST gelijk is aan EAF en driehoek BST gelijkbenig.

Verder, dat CD gelijk is aan K zal als volgt worden bewezen. Omdat kwadraat AG gelijk is aan de kwadraten van K en AB; en hetzelfde kwadraat AG gelijk aan de kwadraten AB en BG met tweemaal rechthoek GBL; daarom zal kwadraat K gelijk zijn aan kwadraat BG met tweemaal rechthoek GBL. Zoals nu BG tot BE is, zo is kwadraat BG met tweemaal rechthoek GBL tot rechthoek GBE met tweemaal rechthoek EBL; vereenvoudigd hebben ze immers die verhouding. Dus ook kwadraat K is tot rechthoek GBE met tweemaal rechthoek EBL, als BG tot BE.
Nu is aan rechthoek GBE gelijk de rechthoek CBD, aangezien CB tot BG is, zoals EB tot BD, wegens gelijkvormige driehoeken CBG en EBD; ze hebben immers de hoeken bij B gelijk en hoek BCG gelijk aan hoek BED. Evenzo is aan tweemaal rechthoek EBL gelijk het kwadraat AB, omdat wegens gelijkvormige driehoeken geldt: zoals SA, dat is tweemaal BE, tot AB is, zo is AB tot BL.
Dus zoals BG tot BE is, zo zal kwadraat K zijn tot rechthoek CBD met kwadraat AB. Maar aan deze twee is gelijk de rechthoek CAD, aangezien in driehoek CAD hoek A doormidden gedeeld wordt door de lijn AB [^]. Dus zoals BG tot BE is, zo is kwadr. K tot rechthoek CAD. En hieruit concluderen we verder, op dezelfde manier als in het voorgaande geval, dat lijn DC gelijk is aan K, door te herhalen⁴⁴): En zoals GB tot BE is, enz.

⁴⁴) Zie p. 203, laatste stukje.

Elk van beide voorgaande Anders.⁴⁵)
Gegeven een ruit ADBC waarvan de zijde DB verlengd is. En gegeven de lijn G. Er moet een rechte ANF zo worden getrokken, dat het afgesneden deel NF gelijk is aan G.

⁴⁵) Ongeveer hetzelfde met datum 16 aug. 1652 in stuk No. XIII, p. 57-59, en in de brief aan van Schooten van 10 dec. 1653, in T. I, p. 256. [...]

[ 209 ]

Laat getrokken worden de diagonaal AB, en aan de kwadraten van G en AB gelijk worden gemaakt kwadraat AH, en getrokken worden HE evenwijdig aan BA. En AE wordt gelijk gesteld aan G, en dezelfde wordt verlengd tot F. Ik zeg dat NF gelijk is aan G.

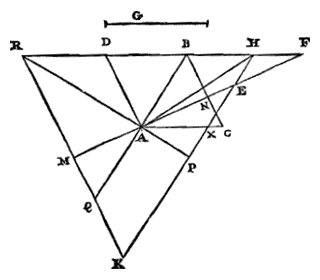
Dat nu tegen HE gelegd kan worden AE gelijk aan G, is duidelijk uit het volgende. Het kwadraat van AH is immers groter dan de kwadraten van AX en XH, daar hoek AXH stomp is. Maar hetzelfde kwadraat AH wordt gelijk gesteld aan de kwadraten AB of HX en G. Dus is kwadraat G of AE groter dan kwadraat AX. Waaruit blijkt dat snijpunt E valt tussen de punten H en X.
Laat verlengd worden BD en eraan gelijk gesteld DR. En RK zij evenwijdig aan DA of BC, en de verlengden van FA, BA en HE ontmoeten deze in de punten M, Q en K; en RA wordt getrokken, en verlengd tot P.

Aangezien dus DR gelijk is aan DB, en RQK evenwijdig aan DA, zal ook MA gelijk zijn aan AN, en QA gelijk aan AB; verder is hoek BAR recht, daar hij in een halve cirkel ligt, want deze drie DB, DA en DR zijn gelijk. En evenwijdig zijn BQ en HEK, dus zijn ook de hoeken bij P recht, en HP zal gelijk zijn aan PK. Dus is kwadraat AH gelijk aan kwadraat AE samen met rechthoek HEK {* 12.2 Elem.⁴⁶)}. Maar hetzelfde kwadraat AH is ook gelijk aan de kwadraten van G of AE, en van AB. Dus zal kwadr. AB gelijk zijn aan rechthoek KEH. En om die reden is KE tot AB als AB tot EH. Maar zoals KE tot AB of QA is, zo is EM tot MA; en zoals AB tot EH is, zo is AF tot FE. Dus EM tot MA is als AF tot FE. En derhalve EA tot AM als EA tot EF. Dan is EF gelijk aan AM, en daarom ook aan AN. En deswege ook FN aan AE, dat is aan de gegeven G. Wat te bewijzen was.

⁴⁶) Zie noot 15, p. 29 [Clavius, p. 192].
[ AH² = AE² + HE² + 2.HE.EP en HE + 2 EP = HP + EP = KP + EP = EK .]

Laat opnieuw gegeven zijn een ruit ADBC, met verlengde zijden BD en BC; en gegeven de lijn G. Er moet een rechte NF worden getrokken die door hoekpunt A gaat, en die gelijk is aan G.

Laat getrokken worden de diagonaal BA, en loodrecht daarop RAL. Als dus G kleiner dan RL wordt gegeven, kan het probleem niet worden geconstrueerd, zoals hierboven ook is gezegd⁴⁷). Als hij echter

⁴⁷) Zie de formulering van het probleem, p. 205.

[ 211 ]

gelijk is, is al gedaan wat gevraagd werd. Laat G dus groter zijn dan RL. In de bijgevoegde tekening zal de constructie, zoals voorgesteld, en het bewijs hetzelfde zijn als in het voorgaande geval.

Doch dit moet hier anders aangetoond worden, dat tegen lijn HE gelegd kan worden AE gelijk aan G. Laat RS gelijk zijn aan RB, en AS verbonden. Aangezien dan in driehoek BAS vanaf de top naar het midden van de basis getrokken is AR, zullen de kwadraten van BR en RA samen genomen, dat is kwadraat BA met tweemaal kwadraat AR, de helft zijn van de kwadraten BA en AS {* per 122. lib. 7. Pappi⁴⁸)}. Dus kwadraat AB tweemaal met viermaal kwadraat AR, dat is met kwadraat RL, zal gelijk zijn aan de kwadraten BA en AS. Daarom, als van beide kanten wordt afgetrokken kwadraat BA, zal kwadraat AS gelijk zijn aan de kwadraten BA en RL, en derhalve kleiner dan kwadr. AH; want dit is gelijk aan de kwadraten AB en G.
Dan is AS kleiner dan AH. Maar hij is groter dan AR. Dus punt S valt tussen R en H; hoek ARH is immers stomp. Dus is RH groter dan RS of RB. En daar wegens gelijkvormige driehoeken RH tot HP is zoals RB tot BA, zal ook HP groter zijn dan BA; en kwadraat HP groter dan kwadraat AB. Maar kwadraat HP met kwadraat PA is gelijk aan kwadraat AH, dat is aan de kwadraten BA en G. Dus daar kwadraat HP groter is dan kwadraat AB, zal omgekeerd kwadr. PA kleiner zijn dan kwadr. G. Dan blijkt dat als om het middelpunt A een omtrek wordt beschreven met straal AE gelijk aan G, deze de lijn HE zal snijden.

⁴⁸) Prop. CXXII van Liber VII in Mathematicae collectiones, ed. Commandino p. 234v: "Gegeven een driehoek ABC, en getrokken een rechte AD die BC doormidden deelt [in D]. Ik zeg dat de kwadraten van BA en AC het dubbele zijn van de kwadraten van AD en DC" (Hultsch, T. II [1877], p. 856-857).

Probl. VIII.

Bij de Conchoïde-lijn te vinden de grenzen van tegengestelde kromming.⁴⁹)
We kennen de Conchoïde die Nicomedes heeft bedacht; waarmee hij ook een hoek in drie gelijke delen heeft verdeeld⁵⁰), en twee middelevenredigen heeft gevonden⁵¹). Laat deze zijn CQD⁵²),

⁴⁹) Historie van dit probleem: p. 110. [Brief aan van Schooten, 23 okt. 1653; beter vond Huygens later de oplossing van H. van Heuraet, in Geometria (1659), p. 258; zie ook T. IX, p. 200: Huygens aan H. Coets, 1687.]
⁵⁰) Zie noot 8, p. 86 [Pappus, lib. 4, prop 32, p. 62r,v]. ⁵¹) Zie stuk No. II, p. 13-15.
⁵²) In de figuur staat de letter D op zijn kop en verschilt de O weinig van een C.

[ 213 ]

met pool G, en richtlijn AB met behulp waarvan hij is beschreven, die GQ loodrecht zal snijden. De eigenschap van deze lijn is dus, dat als vanuit punt G daarnaar een willekeurige rechte wordt getrokken, het deel ervan tussen de conchoïde en de rechte AB onderschept gelijk is aan AQ.

Daar nu blijkt dat een of ander deel van de Conchoïde zoals in de tekening CQD hol is naar de pool G, terwijl het overige van de lijn echter, ook bij doortrekken aan beide kanten tot in het oneindige, andersom is gekromd, is gevraagd op welke manier die punten kunnen worden bepaald waar de tegengestelde buiging een aanvang neemt. En wij hebben hiervoor inderdaad de volgende constructie gevonden.

Laat bij de twee AG en AQ de derde evenredige zijn AE, aan te nemen in de richting van G. En GF wordt gelijk gesteld aan GE. Verder moet GR loodrecht op GQ staan, en gelijk zijn aan tweemaal GA. En de parabool RO wordt beschreven, waarvan de top R is, de as RG en het latus rectum gelijk aan AG. Verder wordt met F als middelpunt en FR als straal een omtrek beschreven, die de parabool snijdt in O; en getrokken wordt OC, evenwijdig aan AB, die de conchoïde ontmoet in de punten C en D. Deze zullen de gevraagde punten zijn bij de begrenzing van de tegengestelde buiging⁵³).

Dit is dan de Algemene constructie. Maar wanneer het kwadraat van AQ niet groter is dan tweemaal het kwadraat van AG, kunnen we het voorgestelde ook door driedeling van een boog tot stand brengen⁵⁴). En wel verschillend, naar gelang AQ groter of kleiner dan AG is. Als hij namelijk kleiner is, moet de omtrek beschreven worden om middelpunt A en met straal AG, en daarbij moet GK gelijk worden genomen aan tweemaal GE, gevonden zoals eerder. En aan de rechte GH, die ligt onder een derde deel van de omtrek KHG, wordt gelijk genomen GM, en door M wordt zoals hiervoor DC getrokken, evenwijdig aan AB.
Wanneer echter AQ groter is dan AG zal er, als het overige op dezelfde manier is samengesteld, slechts dit verschil zijn dat boog KP, die samen met boog GK de halve omtrek vult, in drie gelijke delen moet worden verdeeld, en één van de delen is PH, en de koorde GH wordt gelijk aan GM genomen.

⁵³) Deze constructie dateert van 25 sept. 1653, zie stuk XX, p. 83-85.
⁵⁴) De twee volgende constructies staan in hetzelfde stuk van 25 sept. 1653 op p. 85 en 86.

[ 215 ]

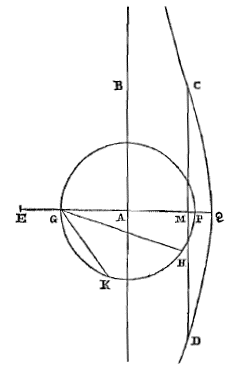
Verder is het Probleem vlak⁵⁵) wanneer AG gelijk is aan AQ. Dan namelijk moet GM gelijk zijn aan een zijde van een gelijkzijdige driehoek in de cirkel ingeschreven. Evenzo wanneer het kwadraat van AQ tweemaal het kwadraat van AG is; dan wordt GM namelijk tweemaal GA.

Maar ook in talloze andere gevallen zal het vlak zijn, waarvan wel die gemakkelijk onderscheiden zullen kunnen worden, welke tot een driedeling van een hoek herleid worden.

F I N I S.

E R R A T A. ⁵⁶)
Pag. 1. lin. 2. post portioni, interpone semicirculo minori. Item tribus hisce locis, Pag. 1. lin. 7. Pag. 3. lin. 3 à fine. Pag. 4. lin. 1. post portio, lege semicirculo minor. Pag. 30. in fig. mutetur P. in B. Pag. 43. lin. penult. lege 31415926533. Pag. 44. lin. 5. pro 3144. lege 3145.

⁵⁵) Deze opmerking ontbreekt in stuk XX, maar is wel te vinden in de brief aan van Schooten van 23 okt. 1653 (T. I, p. 246). [...] Zie ook p. 232, noot 4.
⁵⁶) Met deze errata [1654: p. 72] is rekening gehouden in de tekst; zie noot 1 op p. 120, 121, 123, fig. op p. 161, p. 179. [Gemiste fout: p. 23 (hier p. 153), "HKMN; Dico circulum BN", ... BD.]

Home | Christiaan Huygens | XII | < Grootte van de cirkel (top)