D.   CONCEPT-BRIEF AAN BASNAGE DE BEAUVAL. 1)   Ik zend u zoals ik had beloofd mijn opmerking over Muziek. Ze betreft het voornaamste fundament van deze wetenschap, te weten de bepaling van de Tonen die men waarneemt bij het Zingen en bij het vervaardigen van Instrumenten die voor harmonie gebruikt worden. Zij die hierbij de Theorie enigszins hebben bestudeerd, weten dat het Octaaf verdeeld is in tonen en halve tonen, die niet toevallig of willekeurig zijn gevormd, maar die zo goed als noodzakelijk voortvloeien uit de consonanten; wat er de oorzaak van is dat over de hele wereld deze Tonen of zangtrappen*) niet anders dan dezelfde zouden kunnen zijn, dat wil zeggen van de meest natuurlijke zang, die men de diatonische noemt. Zij weten ook dat, sinds men is begonnen deze zelfde Tonen met wiskundige exactheid te willen bepalen, men enige verscheidenheid heeft gevonden in de verdeling van het octaaf gemaakt in verschillende tijden en door verschillende personen. Want die van de oudheid, die als consonant slechts het octaaf, de kwint en de kwart lieten meetellen, en die geen compositie met verschillende stemmen in praktijk brachten, letten er bij het verdelen van hun octaaf of dubbel octaaf alleen op, dat de intervallen van de tonen hun op bepaalde plaatsen die consonanten in al hun volmaaktheid zouden leveren. Maar in de moderne Muziek, waarin men heeft gevonden dat veelheid van consonanten nodig is en dat alle harmonie van concerten ervan afhangt; heeft men erkend dat men op onze meest volmaakte instrumenten zoals Orgels en Klavecimbels geen van de samenstellingen van Tonen der Ouden kon volgen, ofwel dat het nodig was bij deze   1)  F. 10 r en v van de portefeuille 'Musica' [HUG 27]. Vergelijk, op p. 169 e.v. van T. X, de definitieve tekst van de 'Brief betreffende de Harmonische Cyclus'.  [Zie Rasch 1986, p. 61-69 voor een vergelijking.]   [ *)  Fr.: 'degrez du chant', zie WNT: 'Zang', Zangtrap (Ban), en 'Trap', II, 6 (Stevin en Ban).]

[ 154 ]

instrumenten extra snaren en toetsen toe te voegen, behalve de tussentoetsen of chromatische tonen die men er al met veel reden op had aangebracht 2). omdat men zonder deze toegevoegde snaren verscheidene noodzakelijke consonanten miste, of men had ze zo onvolmaakt dat het oor ze niet kon verdragen. maar aangezien dit aantal extra-toetsen teveel verwarring en moeilijkheid meebracht, heeft men tenslotte gelukkig gevonden wat men noemt de Temperatuur, met behulp waarvan men, door van sommige consonanten iets af te nemen en bij andere iets toe te voegen zonder dat dit evenwel het oor mishaagt, het stelsel heeft gevormd dat men tegenwoordig gebruikt en dat rijk is aan akkoorden; en dat alles levert wat nodig is voor Harmonie van verscheidene Stemmen. Na deze uitvinding, waarover de beste schrijvers zoals Zarlino en Salinas spreken als een van de mooiste en nuttigste zaken die inzake Muziek te vinden zijn, heeft men alle Stelsels der Ouden, en de aanvullingen van snaren van de modernen, links laten liggen; vooral sinds de schrijvers die ik zojuist heb genoemd de beste temperatuur hebben onderzocht en vastgesteld volgens regel en verhouding, waarvan ze onderling de roem betwisten; want ondervinding en noodzaak hadden haar al eerder min of meer ingevoerd; echter zonder dat men er de juiste maat of methode van wist.   Bij deze zelfde schrijvers leert men overigens, dat het voor het in praktijk brengen van deze Temperatuur bij het stemmen van instrumenten nodig is, de consonant kwint te verminderen met een klein bedrag dat een kwart uitmaakt van wat men noemt Komma; wat zo weinig is dat deze vermindering voor het oor nauwelijks waarneembaar is, en in 't geheel niet onaangenaam aandoet; het hele komma is de verhouding tussen de tonen van de hele snaar tegen zichzelf verkort met 1/80 deel. 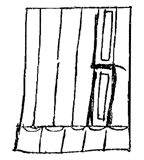Als alle kwinten zo verminderd zijn, volgt eruit dat de kwarten worden   2)  Men kent het bestaan van instrumenten met gesplitste toetsen (b.v. voor dis en as) al in de tweede helft van de 15e eeuw. Ze heetten: enharmonische instrumenten. Anderzijds waren er constructies die toelieten langs mechanische weg de tonen van de boventoetsen te wijzigen. Voor bijzonderheden kan men raadplegen de dissertatie van 1935 van W. Dupont (vergelijk noot 9 van p. 157 en noot 14 van p. 158). De figuur van Huygens, ontleend aan f. 1 van de portef. 'Musica', stelt voor een gesplitste toets. In 1663 bezocht Huygens in Londen iemand die Senti heette die een bepaalde som vroeg "voor een clavecingel die 2 halve toonen gesneden soude hebben, en met het uyttrecken van 't clavier een toon hoogher gaen" (Journaal van de reis naar Londen, p. 176 van H. L. Brugmans Le séjour de Christian Huygens à Paris etc. (1935) [T. XXII, p. 602].

[ 155 ]

vermeerderd met dit zelfde bedrag van een kwart komma, dat de kleine tertsen nog worden verminderd, en de grote sexten vermeerderd, met dit zelfde bedrag. En dat tenslotte de grote Tertsen volmaakt blijven wat van groot belang is. Tenslotte, al deze kleine veranderingen aan de consonanten, waarvan slechts de grote tertsen en de octaven zijn uitgezonderd, verhinderen niet dat alle harmonie wordt gehoord alsof er niets aan scheelde 3).   3)  In de marge:  "dat de stem de temperatuur volgt. — Salinas spreekt over de verdeling 31".  Vergelijk p. 112 hiervoor. E. 1)   HARMONISCHE CYCLUS DOOR VERDELING VAN HET OCTAAF IN 31 DIËZEN 2), GELIJKE INTERVALLEN.   Deze studie wordt voorafgegaan (eveneens f. 16 van de portef. 'Musica') door het Stuk, het programma kan men zeggen, dat we publiceren als Aanhangsel op p. 168 hierna.   § 1.  Zij die de Muziektheorie enigszins bestudeerd hebben (en alleen door hen zal ik begrepen kunnen worden) weten wat de Temperatuur is die dient om de toetsinstrumenten te stemmen die de volmaaktste zijn die we hebben. Zarlino en Salinas spreken erover als een van de mooie en noodzakelijkste dingen, die men in de muziek kon vinden en betwisten elkaar de eer haar te hebben onderzocht en volgens verhouding aan regels onderworpen, want de ondervinding en de noodzaak hadden al de verzwakking van de 5den ingebracht die het voornaamste punt is, maar zonder precieze maat, zonder te weten met hoeveel. Het is ook deze Temperatuur die terecht alle stelsels en verdelingen van het monochord der ouden heeft doen veronachtzamen, als voor het merendeel absurd en onpraktisch; en die   1)  Portefeuille 'Musica' f. 16-19.   2)  Huygens geeft aan het 31 keer herhaalde interval de naam 'diëze' (Gr. diesis), die in het natuurlijke harmonische stelsel het interval aanduidt waarmee een octaaf de som van drie grote tertsen overtreft (grote diëze) ofwel dat waarmee de som van 4 kleine tertsen het octaaf overtreft (kleine diëze). In het pythagoreïsche stelsel wordt hetzelfde woord soms gebruikt om aan te geven het limma (Gr. 'leimma', 256:243). Elk van deze diëzen heeft zijn eigen waarde: die van de grote diëze is 62,6 Cent, van de kleine 40,1 Cent, van het limma 90,23 cent, van die van Huygens 38,71 cent.   In het algemeen wordt het woord 'diesis' door musicologen gebruikt om een klein interval aan te duiden. De manier waarop Huygens deze term toepast komt in principe overeen met die van Aristoxenos, die zijn kleinste interval (¼ toon) 'kleinste enharmonische diesis' noemt (Harm. Elem. [1652], ed. Meibomius, p. 21). Men zou kunnen spreken van een interval-atoom.   Vergelijk het 'interval-atoom' van de Tabula van Meibomius [Dialogus (1655), p. 70] genoemd op p. 6 hiervoor.

[ 156 ]

ons systeem rijker aan akkoorden maakt en meer volgens de natuur van het zingen, dan die van hen waren 3).   Overigens leert men bij die schrijvers 4) dat om haar in praktijk te brengen de kwinten en kleine 6den worden verminderd met een kwart komma, wat een klein interval is, voor het oor nauwelijks waarneembaar, daar het hele komma de verhouding is tussen het geluid van de hele snaar tegen zichzelf verkort met een 81e deel, en dat de 4den en de grote sexten er dientengevolge vermeerderd worden gevonden met ditzelfde kwart komma en dat zo behalve de octaven en grote tertsen die volmaakt blijven, alle akkoorden zodanig worden gewijzigd 5) dat het oor er in het geheel niet door wordt gekwetst, maar ermee tevreden is alsof ze volmaakt waren, wat bekend is naar ik veronderstel, te weten dat de volmaakte kwint te horen is tussen het geluid van de hele snaar en dat van zijn 2/3, ofwel dat de verhouding die deze consonant voorbrengt van 3 tot 2 is, die van de kwart van 4 tot 3; van de grote terts van 5 tot 4, van de kleine terts van 6 tot 5. van de grote sext van 5 tot 3, van de kleine sext van 8 tot 5.   Wat ik nu heb opgemerkt is, dat als men het Octaaf verdeelt in 31 gelijke delen, wat gedaan wordt door 30 middelevenredige lengten te vinden tussen de hele snaar, die men als Harmonische liniaal neemt, en de helft ervan, dat men dan in de tonen die voortkomen bij het laten klinken van al deze lengten apart, een systeem zal vinden, zo dichtbij dat wat voortkomt uit de genoemde Temperatuur, zowel voor de diatonische als voor de chromatische en enharmonische tonen, dat het geheel onmogelijk is dat het meest onderscheidende oor er enig verschil in vindt. En dat toch dit zelfde nieuwe systeem van een heel andere aard zal zijn dan het andere, en nieuwe voordelen zal brengen zowel voor de theorie als voor de praktijk.   De toon zal 5 van deze gelijke delen bevatten, die men diëzen kan noemen, de grote halve toon 3, de kleine halve toon 2, de kleine terts 8, de grote terts 10, de kwart 13, de kwint 18; de kleine sext 21; de grote sext 23; de drietoon 15 en de valse kwint dientengevolge 16 6).   § 2.  Maar alvorens het geringe verschil te laten zien van deze verdeling met die welke ontstaat uit de bovengenoemde Temperatuur, wil ik hier tegemoetkomen aan wat degenen me zouden kunnen tegenwerpen die de boeken van Salinas of van Pater Mersenne hebben gelezen, te weten dat er heel uitdrukkelijk wordt gesproken over deze zelfde verdeling van het octaaf in 31 gelijke delen. Wat   3)  Andere lezing [i.p.v. ceux la]: les leurs.   4)  Zie p. 49 hiervoor, Stuk B. 'Verdeling van het Monochord I'.  [Engl. in Rasch 1986.]   5)  Andere lezing [i.p.v. modifiez]: ordonnez.   6)  Zie het Voorbericht. De drietoon of vermeerderde kwart is een interval samengesteld uit een grote toon, een kleine toon en een tweede grote toon, bijvoorbeeld c - fis-1. De corresponderende verhouding is 45:32 of ongeveer 7:5. De 'valse kwint' is het complement van de drietoon ten opzichte van het octaaf.

[ 157 ]

waar is en ik beken het gaarne. Maar aangezien Salinas van deze uitvinding slechts melding maakt om haar volstrekt te veroordelen, en P. Mersenne haar eveneens verwerpt, zal men mij wel kunnen geloven als ik zeg dat ik het niet van daar heb genomen 7). Maar als dat zo zou zijn, zou ik denken genoeg te hebben gedaan door deze verdeling onderzocht te hebben langs meetkundige weg en haar verdedigd te hebben tegen het onjuiste oordeel uitgesproken door deze twee bekende schrijvers; ik denk dat men mij erkentelijk zou zijn.   Salinas maakt een heel Hoofdstuk waarvan het opschrift is: Over de verkeerde inrichting van een instrument waarvan de vervaardiging in Italië meer dan veertig jaar geleden is begonnen, waarin gevonden wordt dat elke toon in vijf delen is verdeeld 8). Hij zegt dat dit instrument archicymbalum 9) werd genoemd, dat het van een onbekende ontwerper was 10); dat bepaalde bekende musici er veel waardering voor hadden, en in het bijzonder het feit dat het alle intervallen had en alle consonanten (naar ze geloven, zegt hij) naar boven en naar beneden, en dat men er na een bepaalde kringloop terugkwam op hetzelfde geluid, of gelijkwaardig, waar men van was uitgegaan; daarbij ook aantekenend hoeveel van die 31 gelijke delen van het octaaf elke consonant bevatte, evenals ik zojuist heb gedaan. Maar hij voegt er aan toe dat hij heeft geprobeerd zo'n instrument te stemmen, maar dat het een onaangenaam geluid heeft gegeven en dat de oren van allen die het hoorden zo erg kwetste, dat hij eruit concludeert dat een dergelijke stemming zich verwijdert van elke harmonische verhouding, of men nu de zuivere akkoorden beschouwt of de getempereerde 11).   Behalve zijn proef haalt hij nog dit argument aan, ontleend aan de manier waarop men voor dit archicymbalum het interval van de toon in 5 gelijke delen verdeelde, die was: op dit interval vanaf zijn 2 uiteinden twee grote halve tonen nemen, en dan vanwaar deze eindigden twee kleine halve tonen terug. Hij zegt dat hiermee de toon niet in 5 gelijke delen wordt verdeeld. Maar over welke toon wil hij het hebben aangezien het ging over hun toon van 5/31 octaaf, waarvan hij de grootte niet heeft gekend, en misschien zelfs ook niet diegenen die de uitvinders waren, want daarvoor heeft men logaritmen nodig die toen onbekend waren 12).   7)  Zie over deze passage het Voorbericht.       8)  Cap. 27 van Lib. III van De Musica.   9)  We kennen niet de bouw van dit instrument dat Salinas al gezien lijkt te hebben omstreeks 1537 ('citra 40 annos', schreef hij in 1577). Wel is bekend dat er later in de 16e eeuw meer zijn geweest. Vicentino bouwde er een dat hij beschreef in L'antica musica ridotta alla moderna prattica van 1555 (vergelijk noot 9 van p. 144)  [2e ex.].   Arnolt Schlick vermeldt eveneens zulke instrumenten: zie W. Dupont, Geschichte der musikalischen Temperatur, 1935, p. 51.  [A. Schlick, Spiegel der Orgelmacher und Organisten (1511), h. 8, p. 40.]   10)  "... ab eius autore, quisquis ille fuit, Archicymbalum appellatum".       11)  L. c. p. 166.   12)  In de marge:   hoe wist hij de waarde van hun toon. als hij logaritmen had gekend. van de toon die 5/31 van een octaaf uitmaakt. zie Salinas b. 3 h. 15 of 27. H. 15 van boek 3 is getiteld 'Dat er drie inrichtingen van de temperatuur zijn gevonden op de Muziekinstrumenten die we gebruiken; en over de eerste daarvan'. Zie over h. 27 noot 6 van p. 142 hiervoor.

[ 158 ]

Zonder deze was het bijna niet mogelijk 30 gemiddelden te vinden tussen 2 gegeven getallen, zodat Zarlino 13) deze verdeling niet heeft kunnen onderzoeken, en de uitvinders van het archicymbalum ook niet te weten konden komen of het gestemd was volgens wat ze beweerden. Om kort te gaan, deze nieuwe temperatuur die hij zo sterk afwijst kan de meest voortreffelijke van alle worden genoemd, omdat ze alle voordelen heeft die men eraan toekende, naar hij zegt, en ook nog andere waarover ik vervolgens zal spreken, en omdat de harmonie ervan niet onderscheiden kan worden van die welke de gewone Temperatuur geeft die iedereen gebruikt.   § 3.  Om het te laten zien zeg ik ten eerste dat de kwinten van deze verdeling die van de Temperatuur slechts zullen overtreffen met 1/110 Komma 14), een verschil dat door het oor in het geheel niet waargenomen zou kunnen worden, aangezien dat van ¼ Komma in zo geringe mate wordt waargenomen dat dit niet onaangenaam aandoet. En opgemerkt moet worden dat 't met deze 1/110 Komma is, dat de kwinten van de verdeling de volmaakte 5den meer benaderen dan die van de Temperatuur doen; de kwarten worden dientengevolge met slechts 1/110 Komma door die van de Temperatuur te boven gegaan, en ze neigen des te meer naar volmaaktheid van deze Consonant.   De kleine tertsen worden door die van de Temperatuur te boven gegaan met 3/110 of ongeveer   13)  Hiermee wordt waarschijnlijk Salinas bedoeld.   14)  Zie de Tabel van het Voorbericht. Het verschil is 0,20 cent. Het komma bevat 21,5 cent. 1/110 komma = 0,196 cent.   N.a.v. de plaatsen van de 'Cycle harmonique' of 'Novus Cyclus Harmonicus' (Stuk F) [Ned.], waar dezelfde bewering staat, merkt Riemann op, in een noot van p. 359 van zijn Geschichte der Musiktheorie (we hebben het al gezegd in noot 10 van p. 7 hiervoor): "Huyghens ... wirft Salinas und Mersenne vor, dass sie aus Unkenntnis der Logarithmen, die Vorzüglichkeit der 31-stufigen Temperatur nicht hätten erkennen können; nicht um 1/4 des syntonischen Kommas zu klein, sondern um 1/110 desselben zu gross seien die Quinten dieser Temperatur. Nach meiner grossen Tabelle der Tonwerte in Logarithmen auf Basis 2 ... sind aber doch die Quinten um 1/4 Komma zu klein - ich überlasse die Nachprüfung Mathematikern von Fach!". Dupont komt in zijn Geschichte der musikalischen Temperatur (noot 9 hiervoor) uit op dezelfde conclusie met een analoge redenering. Welnu, deze opmerkingen zijn het resultaat van een misverstand. Huygens zegt duidelijk dat zijn kwinten met 1/110 komma de kwinten overtreffen van de gewone temperatuur, d.w.z. van het middentonstelsel. Inderdaad wil zijn hele betoog laten zien dat zijn stelsel maar onmerkbaar verschilt van het middentoonstelsel. Maar de aangehaalde schrijvers laten hem ten onrechte zeggen dat zijn kwint slechts 1/110 komma verschilt van de natuurlijke kwint en bestrijden dan deze vermeende uitspraak.   Laten we in het voorbijgaan opmerken dat Huygens heel goed wist dat Salinas, overleden in 1590, geen logaritmen kon kennen: zie de laatste regels van p. 157.

[ 159 ]

1/37 Komma 15). En de grote sexten gaan de grote sexten van de Temperatuur evenveel te boven; allebei verwijderen ze zich inderdaad van de volmaakte verhouding. Maar men ziet dat dit verschil nog niet waarneembaar zou kunnen zijn.   De grote tertsen tenslotte gaan die van de temperatuur, die volmaakt zijn, te boven met 4/110 of 1/28 Komma 16), wat een zo klein verschil is, dat men ze niet anders dan voor volmaakt zal kunnen houden aangezien het op een snaar van 5 voet geen 1/3 lijn scheelt. De grote halve tonen zoals E, F benaderen er hun ware verhouding iets meer dan in de temperatuur, want daar deze ware verhouding is van 16 tot 15, te weten het verschil tussen volmaakte kwart en grote terts, overtreft de halve toon van de Temperatuur haar met ¼ komma, en de onze met ¼ min 1/22 komma 17) wat deze halve toon alleen maar iets zou kunnen verzachten en goed zou zijn in cadensen 18).   Overigens kan men zeggen dat het slechts voordelig is op de 5den en op de 4den enige volmaaktheid te winnen door op de tertsen iets meer te verliezen, omdat hoe volmaakter consonanten zijn, dat wil zeggen hoe vaker hun trillingen zich verenigen, des te minder het oor hun verandering verdraagt. Zo kan men bij unisono en bij het octaaf niet de minste verandering verdragen. En de kwint is hierin gevoeliger dan de kwart en deze gevoeliger dan tertsen en sexten. Maar, zoals ik al heb aangetoond, alle verschillen van deze 2 Temperaturen zijn onmerkbaar, en er volgt uit dat als een Orgelregister of een klavecimbel gestemd is volgens de gewone Temperatuur, men kan zeggen dat het dit ook zal zijn volgens de nieuwe, voorzover het oor kan onderscheiden. Maar als men daarover toch helemaal voldaan wil zijn, en tegelijk de verdeling van het octaaf in 31 gelijke delen wil hebben, moet men slechts een monochord verdelen volgens de getallen die men ziet in de Tabel die ik geef 19), en met zijn snaar gelijkgestemd met de c van het klavecimbel of orgel, eveneens de andere snaren of pijpen stemmen met de geluiden van de achtereenvolgens verkorte snaar van het Monochord.   En als men vraagt, welk voordeel men haalt uit deze Verdeling aangezien ze tonen geeft die zo lijken op die van de Temperatuur, zeg ik dat er meer dan één zijn. Want   15)  Het verschil is 0,60 cent. 1/110 komma = 0,59 cent.   16)  Het verschil is 0,79 cent. 4/110 komma = 0,78 cent.   17)  In het natuurlijke harmonische stelsel is de grote halve toon 112 cent, in het middentoonstelsel is deze 117,13 en bij Huygens 116,13 cent. Het verschil van de afwijkingen is dus 1 cent of ongeveer 1/22 komma.   18)  Te weten in alle cadensen waarin de bovenstem een halve toon stijgt.   19)  Zie Stuk F hierna, d.w.z. de (Nieuwe) Harmonische Cyclus, T. X, p. 173.  [<]

[ 160 ]

ten eerste leert ze ons dat we, zonder iets te verliezen van het goede effect van de Temperatuur, maar veeleer er iets aan toevoegend, een systeem hebben waarin elke snaar zowel van de tonen als van de halve tonen en diëzen alle consonanten en intervallen omhoog en omlaag blijkt te hebben, en overal op dezelfde manier.   dat in dit systeem de grote halve toon drie vijfde delen van de toon bevat, en de kleine halve toon de andere twee vijfde.   dat het tenslotte een volmaakte Harmonische Cyclus omvat, doordat men ineens stijgend of dalend met het interval kwint, of welk ander dan ook, na een bepaalde omloop terugkeert op de snaar waar men begonnen was 20).   § 4.  Ik zeg bovendien dat men op deze fundamenten een orgelregister of een Klavecimbel kan bouwen, dat zal dienen om te transponeren omhoog of omlaag met zo'n interval als men wil, zoals met de 4de, terts, toon, halve toon, enz. tot aan een diëze of vijfde toon. Wat op gewone instrumenten van deze soort onmogelijk is; en hier wordt het zonder moeite gedaan en zonder de voor transpositie vereiste handigheid te hebben. En opdat degenen die een dergelijk instrument willen laten bouwen weten hoe het aan te pakken zal ik hier de instructie geven.   De buizen of snaren moeten zodanig worden opgesteld dat er 31 in elk octaaf zijn exclusief de laatste snaar, wat gemakkelijk is bij orgels en ook nog bij Klavecimbels, aangezien men er gewoonlijk al 24 snaren zet op die welke twee gelijkgestemde registers hebben en soms nog 6 of 8 andere voor 3 of 4 extra tussentoetsen 21). De stokken die deze buizen of snaren laten afgaan zullen precies van gelijke breedte worden gemaakt, die een vijfde deel van de breedte van een toets moet zijn, en ze zullen dicht bij elkaar gerangschikt worden en alle op dezelfde hoogte, zonder enig verschil. Daarop zal men een beweegbaar klavier plaatsen met gewone toetsen die aan een kant vastgemaakt zullen zijn aan een platte lat die kan schuiven in een andere lat die vastzit zonder er uit te kunnen gaan, wat gemakkelijk is. Van de beweegbare lat zal men aan elke kant 3 of 4 stukken afzagen, elk van de breedte van een toets, wat zal maken dat de toetsen   20)  Aan deze eigenschap dankt de korte verhandeling van Huygens haar titel (Cycle Harmonique). Ze komt onmiddellijk voort uit het feit dat elk interval een geheel veelvoud is van de diëze. Als het beschouwde interval van n diëzen is, leidt een stijging over een reeks van 31 van deze intervallen tot het ne octaaf van de grondtoon.   21)  Zo was het b.v. voor het Gravicembalo in 1548 gebouwd voor Zarlino door Domenico de Pesaro: tussen b en c en evenzo tussen e en f was een witte toets ingevoegd; tussen de andere witte toetsen steeds twee gekleurde boventoetsen [fig.]. Enkele malen wordt melding gemaakt van een splitsing in tweeën van de zwarte toets tussen d en e om de noten dis en es te onderscheiden, en zelfs van die tussen g en a om as en gis te onderscheiden. Vergelijk Dupont l. c. p. 50 e.v.  Een 'clavemusicum omnitonum' van 1606, met 31 toetsen voor elk octaaf, is bewaard gebleven (Dupont, p. 53).   De Nederlandse lezer kan ook raadplegen het werk van Mevr. Bertha van Beynum - von Essen, Bouw en Geschiedenis van het Klavier (Rotterdam, Brusse, 1932) [2e druk 1948].

[ 161 ]

die vastzitten aan deze stukken overgebracht kunnen worden van de ene kant van de onbeweeglijke lat naar de andere, opdat de beweegbare zoveel kan opschuiven of teruggaan als nodig is volgens de merktekens die men erop zal schrijven. Ik heb eertijds zulke beweegbare klavieren voor klavecimbels laten maken toen ik in Parijs was, om ze op gewone klavieren van Klavecimbels te plaatsen, en zelfs voor die welke hun gewone klavier hadden waarbij het nodig was dat het klavier dat ik er opzette tegelijk met de hoogten van de toetsen en van de tussentoetsen gelijk was, opdat de toetsen zonder belemmering konden glijden. En deze uitvinding werd goedgekeurd en nagemaakt door grote meesters, die er gemak en genoegen in vonden 22).   Over de uitvinding die ik hier behandel moet nog gezegd worden dat men onderaan elke toets en tussentoets van het beweegbare klavier kleine punten moet vastmaken, zodanig opgesteld dat ze geplaatst zijn om direct te drukken op de stokken die eronder zijn en die overeenkomen met de tonen van die toetsen, waarvoor zorg en precisie nodig is. Maar als ze goed zijn afgesteld in de ene ligging zullen ze goed zijn in alle andere wegens de gelijke breedte van de stokken.   Er is ook dit gemak dat men zonder snaren toe te voegen extra tussentoetsen op het klavier kan hebben voor enharmonische tonen die voornamelijk dienen om akkoorden aan te vullen waarmee men te maken heeft als bepaalde tonen worden gespeeld. Want deze toegevoegde toetsen zullen even goed als de andere in alle transposities hun juiste snaren vinden, zoals zal blijken in de volgende Tabel 23) waar de meest nodige van deze toe te voegen tussentoetsen zijn aangegeven.   § 5.  Ik zal hier nog een opmerking vermelden bij het voordeel van deze nieuwe temperatuur die is, dat het interval van de drietoon er overal in is bevat met de verhouding van 7 tot 5, slechts 1/12 komma tekortkomend, en dientengevolge dat van de valse kwint evenveel boven de verhouding van 10 tot 7; terwijl deze verschillen in de gewone temperatuur 1/7 komma zijn 24). Nu zeg ik dat deze intervallen van 7 tot 5 en van 10 tot 7 iets harmonieus hebben als ze met aandacht worden beschouwd (althans   22)  In juli en augustus 1669 (T. VI, p. 473 en 484) in brieven aan zijn broer Lodewijk, vermeldt Huygens zijn "uitvinding voor het klavecimbel" of "uitvinding van mijn beweegbaar klavier", waarvan hij zegt een exacte en vrij lange beschrijving gestuurd te hebben aan hun vader. Deze bezitten we niet, want de brieven gewisseld tussen Huygens en zijn vader tijdens het verblijf van de eerste in Frankrijk ontbreken; vergelijk noot 3 van p. 7 van T. XVIII.   23)  Zie de Tabel waarmee ons Voorbericht eindigt (p. 146).   24)  Het interval 7:5 bedraagt 582,52 cent. Voor de juiste waarde 45:32 van de drietoon vindt men 590,22 cent. 15 diëzen verschillen inderdaad 1,87 cent of 1/12 komma van het genoemde aantal 582,52 cent.

[ 162 ]

met mijn oor bevind ik het zo) en dat men ze onder de consonanten 25) zou kunnen rekenen, wat de meester-componsten er ook van kunnen zeggen, die ze anders rangschikken onder de valse verhoudingen 26). Daarmee kan het net zo zijn als met de grote en kleine Tertsen bij de ouden die ze nooit hebben willen erkennen als consonanten, zoals men tegenwoordig nog beweert dat ze maar onvolmaakt zijn en dat de volmaakte zijn het octaaf, de kwint en de kwart, wat een heel slecht gefundeerd onderscheid is 27). Maar voor het bewijzen deze nieuwe tegenspraak die ik zojuist naar voren heb gebracht aangaande de drietoon en de valse kwint, zal het nodig zijn iets te zeggen aangaande de oorsprong 28) van Consonanten in het algemeen.   § 6.  Men weet dat wat 2 snaren 29) goed doet samenklinken de slagen of trillingen zijn die ze in de lucht veroorzaken, die vaak en op regelmatige wijze tot vereniging komen, en dat hoe veelvuldiger de verenigingen zijn, des te meer wordt de consonant als volmaakt beoordeeld, of op zijn minst van uitstekende waarde. Zo verenigen de slagen zich bij het octaaf elke keer dat de lage snaar 1 trilling heeft gemaakt en de andere 2, bij de kwint bij elke 2 trillingen van de ene en 3 van de andere, bij de kwart 3 en 4, bij de grote terts 4 en 5, bij de kleine terts 5 en 6. Men beweert dat alle consonanten zijn beperkt tot het getal 6 30), want hoewel in de   25)  Vergelijk de laatste alinea van p. 37 hiervoor.   26)  In de marge:  Mersenne vindt geen reden. 8 tot 5, waarom dit het oor behaagt. Dient om te stemmen. Versiert gezang. Zeer vaak gebruikt interval dat meer dan men denkt dient voor het maken van mooie liederen. Welke plaats men er ook aan geeft, ze zullen er niet minder mooi om zijn. Wordt de grote sext niet bijna altijd gered door het octaaf. Men intoneert het gemakkelijk. Dat van 7 tot 4 is er maar 2 keer. Dat maakt hem minder te verdragen. 7 tot 6 en 7 tot 3 komen hier niet voor. — Ik luister niet naar degenen die een autoriteit aanhalen.   27)  De opmerking over Mersenne slaat ongetwijfeld op zijn beschouwingen over het aantal consonanten in boek 1 'Van de Consonanten', Prop. 33: "Waarom er maar zeven of acht eenvoudige consonanten zijn".   Dit onderscheid wordt o.a. gemaakt door Zarlino, Istitutioni Harmoniche Parte III cap. 6 "Divisione delle Consonanze nelle Perfette e nelle Imperfette". Het berust op het feit dat de getallen die de verhoudingen aangeven van alle 'perfecte consonanten' worden omvat door de reeks 1, 2, 3, 4, terwijl om alle consonanten zonder uitzondering uit te drukken de reeks 1, 2, 3, 4, 5, 6 nodig is, de 'senarius', vergelijk noot 30 hierna.   28)  Andere lezing [i.p.v. "l'origine"]: la nature.   29)  In de marge:  Hetzelfde is het geval bij orgelpijpen.   30)  Huygens zinspeelt hier op de theorie van de 'senarius' ontwikkeld door Zarlino in zijn Istitutioni Harmoniche, Parte I, cap. 13-16, en door Salinas in zijn De Musica, Lib. II, cap. 12, 24, 25. Volgens deze theorie zouden de verhoudingen van de consonante intervallen alle omvat zijn in de getallenreeks 1, 2, 3, 4, 5, 6.

[ 163 ]

kleine sext de slagen zich pas verenigen bij elke 5 trilingen van de lage snaar en 8 van de hoge, ziet men dat deze 8 vier dubbele trillingen maken tegen de 5 van de andere snaar 31), en dat zo deze consonant binnen het getal 6 geacht kan worden te zijn; en dat ze nauwelijks in zachtheid hoeft onder te doen voor die van de grote terts; en hetzelfde is het geval met de 3 tegen 8, en de 3 tegen 10, die de Elfde en de Dertiende maken.   Omdat nu 5 slagen tegen 6 consonantie maken, waarom beweert men dan dat 6 tegen 7 dit helemaal niet doen, noch 5 of 4 of 3 of 2 tegen 7.   Pater Mersenne bekent 32), na lange tijd gezocht te hebben naar een of andere reden daarvoor, dat hij er geen zou kunnen vinden die goed is. En ik geloof dat er inderdaad geen is, omdat men iets verkeerds veronderstelt, want aangezien veelvuldige vereniging van slagen een consonant maakt, komt deze vereniging vrij vaak voor als tegen 5 of 4 of 3 of 2 slagen van de lage snaar er 7 slagen van de hoge worden gemaakt, maar wat sommige van deze consonanten onaangenaam maakt is, dat hoewel het interval van elk zich bevindt in de tonen van ons systeem, deze intervallen nooit of zeer zelden worden gebruikt in de opeenvolging van onze zang, wat tegelijk maakt dat men na deze consonant te hebben getroffen niet kan vinden waar men vervolgens heen kan gaan. Wat deze consonant ongetwijfeld heel erbarmelijk moet maken, aangezien zelfs de voortreffelijkste van alle, als men die slaat op snaren die helemaal verwijderd zijn van de Toon of Toonaarden die men speelt, eerst geen consonant schijnt, en het oor buitengewoon kwetst, zoals wanneer men na de cadens te hebben gemaakt in D, de kwint C G aanslaat.   Maar de consonanten van 5 slagen tegen 7 bevinden zich op verscheidene plaatsen op onze klavieren en evenzo die van 10 of 5 dubbele slagen tegen 7 (aangezien het zoals gezegd drietonen en verminderde kwinten zijn, waarvan er 6 van elk zijn) en ze maken heel mooie intervallen in de zang; ze hebben ook naburige consonanten die er aangenaam op volgen; dus er ontbreekt niets aan van wat de andere consonanten hebben en ze moeten hun plaats krijgen na de andere, die het voordeel hebben dat ze uit eenvoudigere verhoudingen bestaan.   En als men wil argumenteren 33) dat ze vals zijn omdat men ze redt, de ene met sexten, de andere met tertsen, kan men antwoorden dat de 4 er meestal ook behoefte aan heeft gered te worden, dat de grote sext eveneens bijna altijd wordt gered door het octaaf. Weliswaar zijn deze sexten en tertsen de beste akkoorden om te volgen op die drietonen en verminderde kwinten, maar daaruit kan men niet concluderen dat het valse intervallen zijn.   31)  In de marge:  En dat deze snaar van 8 trillingen slechts de replica in het octaaf is van die welke de grote terts maakte met de snaar van 5 trillingen.   32)  Zie de propositie van Mersenne (p. 88 van Harmonie universelle) aangehaald in noot 26.   33)  Andere lezing [i.p.v. "argumenter"]: prouver, inférer.

[ 164 ]

Ik heb gezegd dat de intervallen van 6, 4, 3, 2, tegen 7, zich ook bevinden in de tonen van ons systeem. Want inderdaad: de snaren die de overbodige seconden van F en G maken, van B en C, en van M en F verenigen hun slagen bij elke 6 trillingen van de ene tegen 7 trillingen van de andere, zo dichtbij dat er maar 1/5 komma valt aan te merken op deze verhouding.   Dientengevolge overschrijden de verminderde septiemen van C B, van G F en van F M de verhouding van 7 tot 12 met slechts 1/5 komma.   Behalve dat moet het interval van 3 tot 7 even goed klinken als ...