S T E L L I N G 1 1:
Gegeven een driehoek loodrecht op de horizon, de basis horizontaal, en op elk der andere zijden een rollende bol, in evenwicht met elkaar. Zoals de rechterzijde van de driehoek tot de linker, zo is het gewichtseffect van de bol op de linkerzijde, tot het gewichtseffect van de bol op de rechterzijde.
W E S E N D E een driehouc wiens plat {Planum.} rechthouckich op den sichteinder {Horizontem.} is, met sijn grondt daer af evewidich, ende op elck der ander sijden een rollende cloot met malcanderen evewichtich:
Ghelijck des driehoucx rechter sijde tot de slincker, also t'staltwicht des cloots op de slincker sijde, tottet staltwicht des cloots op de rechter sijde.
Gegeven:
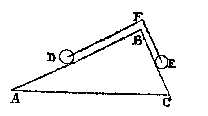
Driehoek ABC staat loodrecht op de horizon. Basis AC is horizontaal.
AB is dubbel zo groot als BC.
Op AB ligt een bol D, op BC een bol E,
met gelijk gewicht en even groot.
Te bewijzen:
Zoals AB 2 tot BC 1, zo is het gewichtseffect van bol E tot het gewichtseffect van bol D.T G H E G H E V E N. Laet ABC een driehouck wesen diens plat sy rechthouckich op den sichteinder, ende den grondt AC evewydich vanden sichteinder, ende op de sijde AB, die dobbel sy an BC, ligghe een cloot D, ende op de sijde BC een cloot E, evewichtich ende evegroot met den cloot D.
T' B E G H E E R D E. Wy moeten bewysen dat ghelijck de sijde AB 2, tot BC I, alsoo t'staltwicht des cloots E, tottet staltwicht des cloots D.
Voorbereiding:
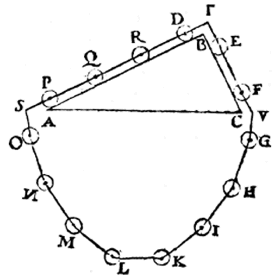
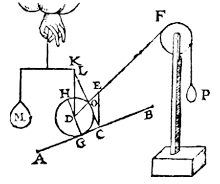
Maak rondom de driehoek ABC een krans van veertien bollen, even groot, met gelijk gewicht, en even ver van elkaar.Ze zijn aaneengesnoerd en kunnen draaien om hun middelpunt. Op BC passen twee bollen, op BA vier.
S, T en V zijn vaste punten waarover het snoer kan glijden: als je aan de krans trekt, rollen de bollen op AB en BC.
T' B E R E Y T S E L. Laet ons maecken rondtom den driehouck ABC eenen crans van veerthien clooten, evegroot, evewichtich, ende evewijt van malcanderen, als E, F, G, H, I, K, L, M, N, O, P, Q, R, D, al ghesnoert an een lini, streckende door haer middelpunten {Centra.}, also dat sy op die middelpunten drayen mueghen;
Datter oock twee clooten passen op de sijde BC, ende vier op BA, dat is ghelijck lini tot lini, also clooten tot clooten; laet oock an S, T, V, drie vastpunten staen, over welcke de lini ofte t'snoer der clooten slieren mach, also dat de twee deelen des snoers die boven den driehouck staen, evewydich {Parallela.} sijn vande sijden AB, BC; Inder voughen dat alsmen den crans an d'een ofte d'ander sijde neertrect, soo rollen de clooten op de linien AB, BC.
Bewijs:
Als het gewichtseffect der vier bollen op AB niet gelijk is aan dat van de twee op BC, is het ene groter dan het andere.Neem aan dat van de vier op AB.
Maar de vier eronder zijn in evenwicht met de vier onder BC. Dan zal de krans links naar beneden gaan en rechts omhoog.
T' B E W Y S. Soo t'staltwicht der vier clooten D, R, Q, P, niet even en waer met het staltwicht der twee clooten E, F, t'een of t'ander sal swaerder sijn, latet wesen (soot mueghelick waer) der vier D, R, Q. P;
Maer de vier clooten O, N, M, L, sijn evewichtich met de vier clooten G, H, I, K, de sijde dan der acht clooten D, R, Q, P, O, N, M, L, is swaerder na de ghestalt dan de sijde der ses clooten E, F, G, H, I, K: maer want het swaerste altijdt het lichtste overweeght, de acht clooten sullen neerwaert rollen, ende d'ander ses rijsen:
Laat dan de bol D van de linksom draaiende krans gevallen zijn tot waar nu bol O is, en bol K gestegen tot waar nu bol F is.
Dan heeft de krans weer dezelfde opstelling, dus er blijft beweging.
Maar dit zou een eeuwige beweging zijn, en dat kan niet (perpetuum mobile).
Latet soo wesen, ende D sy ghevallen daer nu O is, ende E, F, G, H, sullen sijn daer nu P, Q, R, D, ende I, K, daer nu E, F, sijn.
Maer dit soo wesende, den crans der clooten sal alsulcken ghestalt hebben als sy te vooren dede, ende sullen om de selve redenen de acht clooten ter slincker sijde wederom staltwichtigher sijn dan de ses clooten ter rechter, waer duer de acht clooten wederom neer sullen rollen, ende d'ander ses rijsen, welcke valling ter eender, ende rijsing ter ander, om dat de reden altijdt de selve is, altijdt ghedueren sal, ende de clooten sullen uyt haer selven een eeuwich roersel maken, t'welck valsch is.
Het linkerdeel D t/m L is dus in evenwicht met het rechterdeel E t/m K.
En als je links en rechts evenveel van die gelijke bollen weglaat, blijft er evenwicht.
Als je de bollen onder AC weglaat blijft er evenwicht.
Dus de vier op AB zijn in evenwicht met de twee op BC.
Dan moet het gewichtseffect van bol E tweemaal dat van bol D zijn.
Conclusie: zols AB 2 tot BC 1, zo is het gewichtseffect van bol E tot het gewichtseffect van bol D.
Het deel dan des crans D, R, Q, P, O, N, M, L, is evestaltwichtich met het deel E, F, G, H, I, K:
Maer van sulke evewichtighe ghetrocken evewichtighe, de resten sijn evewichtich, laet ons dan van dat deel trecken de vier clooten O, N, M, L, ende van dit de vier clooten G, H, I, K, (welcke even sijn ande voornoemde O, N, M, L,) de resten D, R, Q, P, ende E, F, sullen evestaltwichtich sijn,
Maer wesende dese twee evestaltwichtich met die vier, E sal tweemael staltswaerder sijn als D.
Ghelijck dan de lini BA 2, tot de lini BC I, also t'staltwicht des cloots E, tottet staltwicht des cloots D.
[ Zie ook Wikipedia: Clootcransbewijs.]
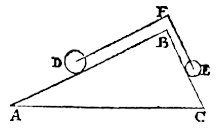
Gevolg 1
ABC is weer zo'n driehoek, AB = 2 BC.Op AB ligt een bol D, op BC een bol E met het halve gewicht van D. Bij F is een vast punt waarover DFE kan glijden.
Er is weer evenwicht, dus AB : BC = D : E.
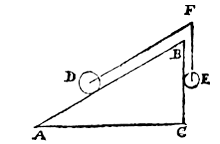
Gevolg 2
Nu is BC vertikaal, AB = 2 BC.Weer is er evenwicht, en AB : BC = D : E.
A E T ABC een driehouck sijn als vooren, wiens sijde AB dobbel sy an BC, ende laet op AB ligghen een cloot D, ende op de sijde BC een cloot E evewichtich anden helft van D, ende an F sy een vastpunt daer over de lini DFE. (te weten uyt het middelpunt {Centro.} des cloots D over F tot int middelpunt des cloots E) slieren mach, alsoo dat DF evewydich blijve van AB, ende FE van BC. Dit also sijnde, anghesien de vier clooten P, Q, R, D, hier vooren, evestaltwichtich waren met de twee clooten E, F, so sal desen cloot D, evestaltwichtich sijn teghen de cloot E: want ghelijck die P, Q, R, D, tot E, F, also dese D tot E: Daerom ghelijck de lini AB, tot BC, alsoo den cloot D tot den cloot E.
A E T ons nu d'een sijde des driehouckx als BC (ande welcke AB dobbel is) rechthouckich stellen op AC als hier neven [boven]; Ende den cloot D die dobbel is an E, sal noch met E evestaltwichtich sijn, want ghelijck AB tot BC, also den cloot D tot den cloot E.
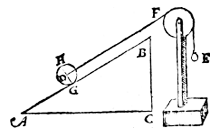
Gevolg 3
Bij F zetten we nu een katrol*). E is geen bol meer, maar houdt hetzelde gewicht.Er blijft evenwicht, dus AB : BC = D : E.
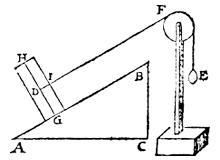
Gevolg 4
Nu een balkje in plaats van bol D, van gelijk gewicht, met de as GH loodrecht op AB.DF blijft evenwijdig met AB.
Nog steeds is AB : BC = D : E.
A E T ons nu inde plaets van t'punt F, stellen een caterol als hier neven [boven], also dat de scheefheflini van D naer F evewydich blijve van AB, ende inde plaets vanden cloot E sy eenich wicht van form soot valt, maer evewichtich anden cloot E: t'selve is noch evestaltwichtich met D, Daerom ghelijck AB tot BC, alsoo noch den cloot D tottet ghewicht E.
N G H E S I E N den cloot des 3en vervolgs naect de lini AB, in t'punt G, als vastpunt, soo sal den as GH rechthouckich sijn op AB {18.v.3.B E.};Daerom laet ons weren den cloot, ende stellen in die plaets den pilaer D evewichtich met den cloot, alsoo dat den as GH (diens vastpunt G) rechthouckich sy op AB, ende de scheefheflini tusschen DF noch evewydich van AB, ende sniende de sijde des pilaers in I, Als hier nevens [boven].
Ende is openbaer dat ghelijck AB tot BC, (dat is dobbel als vooren) also den pilaer D tottet t'ghewicht E.
[ *) Hoe een goede katrol gemaakt wordt voor dit soort proeven staat in Weeghdaet, p. 17.]
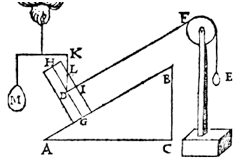Gevolg 5
Nu trekken we uit het midden D van het balkje de vertikale lijn DK, die de zijde snijdt in L.
Dan is AB : BC = LD : DI.
Daarom is LD : DI = D : E.
M weegt op tegen het balkje (zonder AB en E), dus LD : DI = M : E.
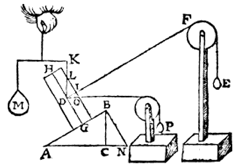
Gevolg 6
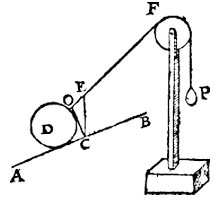
Verleng AC tot N; trek BN, en DO, die de kant van het balkje snijdt in O, met hoek IDO = hoek CBN.
Nu nog een katrol erbij, met P.
Als P het balkje in die stand houdt (zonder M en E) geldt: M = P.
A E T ons trecken de hanghende lini uyt het middelpunt {Centro.} des pilaers D als DK, sniende de sijde des pilaers in L, t'welck soo sijnde, den driehouck LDI is ghelijck an den driehouck ABC, want de houcken ACB ende LID sijn recht, ende LD is evewydich van BC ende DI van AB: Daerom ghelijck AB tot BC, alsoo LD tot DI; Maer ghelijck AB tot BC, alsoo den Pilaer tot t'ghewicht E door het 4e vervolg, daerom ghelijck LD tot DI, also den pilaer tot E.Laet ons nu ande lini KD voughen t rechthefwicht M met den pilaer evestaltwichtig, t'selve ghewicht M sal met den pilaer evewichtich sijn door het 14e voorstel: Daerom ghelijck LD tot DI, also M tot E.
A E T ons trecken BN, sniende de voortghetrocken AC in N: Insghelijcx DO, sniende de voortghetrocken LI dat is de sijde des pilaers in O, ende also dat den houck IDO, even sy anden houck CBN. Laet ons oock voughen an DO t'scheefhefwicht P, dat den pilaer (de ghewichten M, E gheweert sijnde) in die standt haude. [...]Ende ghelijck DL tot DO, alsoo t'staltwicht van DL, tottet staltwicht van DO, dat is, also M tot P. Inder voughen dat dese everedenheydt {Proportio.} niet alleen en bestaet inde voorbeelden, alwaer de heflini als DI rechthouckich is op den as, maer op allen houcken.
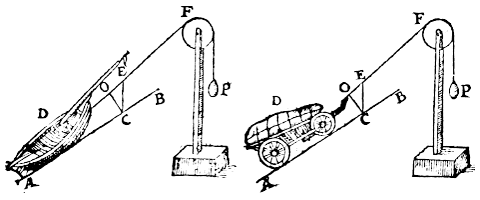
Ook voor een bol zoals hier geldt
(met CL loodrecht op AB):
LD : DO = M : P.
M = D, dus LD : DO = D : P.
Trek CE vertikaal, dan geldt:
LD : DO = CE : EO = D : P.
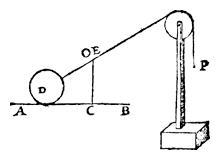
Voor de duidelijkheid:
CE : EO = D : P.
' V O O R G A E N D E mach oock verstaen worden van een cloot ligghende op een lini AB als hier nevens [boven], alwaer wy segghen als vooren, gelijck LD tot DO, alsoo M tot P (welverstaende dat CL rechthouckich ghetrocken is op AB, dat is evewydich met den as GH des cloots D) maer t'ghewicht M is even an den cloot D, daerom segghen wy ghelijck LD tot DO, also t'ghewicht des cloots, tot P. Maer want LD ende DO binnen t'lichaem des cloots niet bequamelick en connen beschreven worden, so laet ons trecken de hangende CE, ende sullen dan hebben buyten t'lichaem een driehouck CEO, ghelijck anden driehouck LDO, welcker lijckstandighe {Homologa.} sijden sijn LD met CE, ende DO met EO, daerom ghelijck LD tot DO, alsoo CE tot EO, ende vervolghens ghelijck CE tot EO, alsoo t'ghewicht des cloots, tot P.
A E T ons nu tot meerder claerheydt dit alleen stellen sonder d'ander linien als hier neven [boven], alwaer wy segghen ghelijck CE tot EO, also t'ghewicht des cloots D, tot P. 
Waaruit ook blijkt: 
N D E dit niet alleen van clooten maer van ander lichamen slierende, ofte rollende, op punten ofte linien als hier onder [boven] (daerwy eyghentlicker af handelen sullen inde 
A E R uyt oock blijckt, dat wesende de lini AB evewydich vanden sichteinder {Horizonte.} als hier nevens [boven], dat CE ende CO dan in een selfde lini sullen vallen, waer duer tusschen E en O gheen langde en sal sijn, ende vervolghens CE en sal tot EO gheen reden hebben, daermen by verstaen sal dat een swaerheydt inde plaets van P hoe cleen sy mocht wesen, en sal niet evestaltwichtich connen sijn teghen t'lichaem D, maer salt (wisconstelick {Mathematicè.} verstaende) voorttrecken hoe swaer het sy: