| [ < 466 ] | [ v ] |
A D D I T I O N.
uelque temps aprés que j'eus achevé d'escrire ce qui precede, ayant receu & examiné le journal du voiage, qui, par ordre de Messieurs les Directeurs de la Compagnie des Indes Orientales, a esté fait, avec nos Horloges à pendule, | 153 | jusqu'au Cap de Bonne Esperance; & du dépuis ayant encore lû le tres sçavant ouvrage de Mr. Newton, dont le titre est Philosophiae Naturalis principia Mathematica 22); l'un & l'autre me fournit de la matiere pour étendre d'avantage ce Discours. Et premierement, quant aux differentes longueurs des Pendules dans divers Climats, dont il a aussi traité, je crois avoir, par le moien de ces Horloges, non seulement une confirmation évidente de cet effect du mouvement de la Terre, mais aussi de la mesure de ces longueurs, qui s'accorde tres bien avec le calcul que je viens d'en donner. Car ayant corrigé & rectifié, suivant ce calcul, les Longitudes qu'on avoit mesurées par les Horloges, au retour du Cap de B. Espe. jusqu'au Texel en Hollande, (car en allant elles n'avoient point servi) j'ay trouvé que la route du vaisseau en estoit beaucoup mieux 22) Nous avons cité dans la note 19 les propositions de Newton qui traitent des matières contenues dans la présente Addition [Prop. XIX, XX; Franç.]. |
| [ 467 ] | [ v ] |
|
marquée sur la Carte, qu'elle n'estoit sans cette correction; & si bien, qu'en arrivant à ce Port, il n'y avoit pas 5 ou 6 lieues d'erreur dans la Longitude ainsi rectifiée. Supposant que celle dudit Cap avoit esté bien prise par les P. P. Jesuites, lors qu'ils y passerent en l'année 1685, en allant à Siam*); & qu'elle est de 18 degrez plus à l'Est que celle de Paris; ce que je sçay encore d'ailleurs ne s'éloigner guere de la verité 23). Le detail de toute cette affaire est deduit au long dans le Raport que j'ay fait, touchant ce voiage des Pendules, aux dits Messieurs les Directeurs. Sur lequel raport, apres l'avoir fait examiner par des personnes intelligentes, il leur a plû d'ordonner qu'on fist une seconde epreuve; pour s'assurer par plusieurs experiences de la bonté de cette invention. L'on verra quel sera le succés de cet autre voiage, & particulierement en ce qui est de la variation des Pendules. estant certain que, pour la bien connoitre, ces Horloges donnent un moyen plus seur, par leur acceleration & retardement, que n'est celuy de mesurer actuellement la longueur du pendule à Secondes en differens païs. Cependant, | 154 | parce que dans l'essay, dont je viens de parler, l'experience s'est si bien accordée avec ce que j'avois trouvé par raisonnement, je m'y fie assez pour vouloir continuer cette speculation, en cherchant premierement, quelle est donc la forme de la Terre, puisque, comme il a esté dit, elle n'est pas Spherique. Il est bon pour cela de la considerer comme toute couverte d'eau, ou comme si toute sa masse n'estoit autre chose. Et alors il paroit, par ce qui a esté expliqué cy dessus, que la surface doit estre telle, que, dans quelque endroit que ce soit, le fil, qui soutient un plomb, l'aille rencontrer à angles droits; ayant égard à la pesanteur ensemble, & à la force centrifuge, qui detourne le fil de la direction vers le centre. Parce que si le fil ne rencontroit pas la surface à angles droits, elle ne pourroit pas demeurer en l'assiette où elle est. |

|
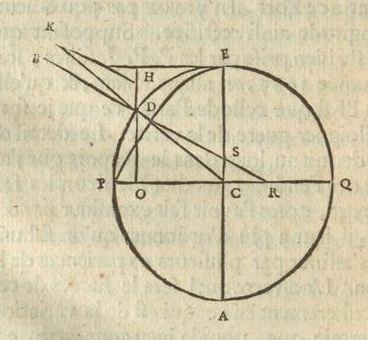
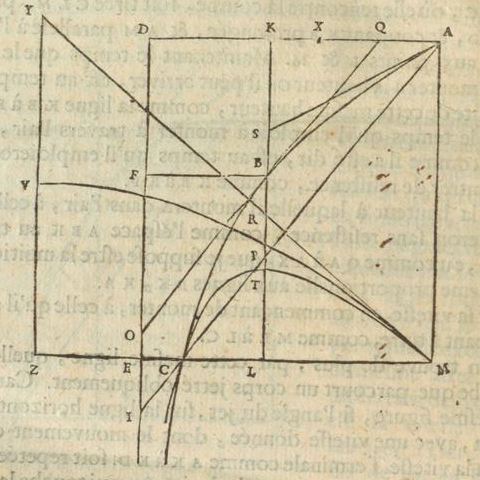
Supposé donc les mesmes choses, que dans la derniere figure [<] du discours precedent, & aussi ce qui en a esté expliqué; mais faisant la forme de la Terre un peu diminuée & applatie vers les Poles, en sorte que l'axe PQ soit plus court que le diametre EA; soit menée BDSR parallele à KH, coupant EA, PQ en S & R. Puisque le fil KH, qui soutient le plomb, ou plutost sa parallele BD, doit rencontrer
*) [ Cf. Histoire de l'Académie royale des sciences, 1729 (T. 7.2), 611-3, 'Observation pour la Longitude du Cap de Bonne-Esperance' (2-4 juin 1685).] 23) Comme nous l'avons dit aussi à la p. 652 du T. XVIII, il n'est pourtant pas exact que le Cap de Bonne Espérance aurait une longitude orientale de 18° par rapport à Paris. Les cartes modernes donnent 16° 10' pour cette longitude. |
| [ 468 ] | [ v ] |
|
la surface de la mer à angles droits; & puisque ce fil pend en sorte, que KD est à DH, ou DC à | 155 |
CS, comme la pesanteur absoluë à la force centrifuge en D; laquelle raison est composée de celle de la pesanteur absoluë, à la force centrifuge en E, qui est comme de 289 à 1, & celle de cette force à la force centrifuge en D, qui est comme EC à DO; il paroit que la nature de la Ligne courbe EDP est determinée par la proprieté de sa perpendiculaire, comme DR; c'est-à-dire qu'en menant une telle perpendiculaire, tousjours la raison de DC à CS doit estre composée d'une raison donnée, & celle de EC à DO. Ou bien, comme on en peut inferer facilement, que la raison de DO à CS, ou de OR à RC doit estre composée de la dite raison donnée, & de celle de EC à CD. Or il est difficile de trouver ainsi des lignes courbes par la proprieté donnée de leurs perpendiculaires, ou, ce qui est la mesme chose, par la proprieté de leur Tangentes 24). Mais il y a un moyen assez aisé pour cette courbe icy, qui est fondé sur l'equilibre de certains canaux, dont Mr. Newton a donné la premiere idée.
Le canal qu'il suppose est representé dans nostre figure par ECP, faisant un angle droit au centre de la Terre. Il faut le concevoir comme ayant quelque peu de creux, & rempli d'eau. Ce qui estant, il est certain que les deux jambes, EC, CP, se doivent tenir en équilibre, si l'on suppose que la Terre, estant toute composée d'eau, prend une figure, dont les diametres soient EA & PQ: parce qu'autrement, cette eau du canal, ne demeureroit pas non plus dans son assiette en la concevant sans canal, contre ce qu'on suppose. d'où il est aisé de trouver la raison de EA à PQ. Car en posant EC
Pour trouver en suite quelle est la ligne courbe EDP, je m'imagine le canal plein d'eau ECD, & menant DO perpendiculaire sur l'axe PC, je fais CO 24) Huygens s'était surtout occupé en 1687, de concert avec Fatio de Duillier, du "problème renversé des tangentes", mais seulement pour un certain genre de courbes: voyez les p. 491 - 502 du T. XX. Il devait reprendre cette recherche en 1691 en se laissant de nouveau guider, peut-on dire, par le jeune mathématicien suisse (T. XX, p. 506 - 541). |
| [ 469 ] | [ v ] |
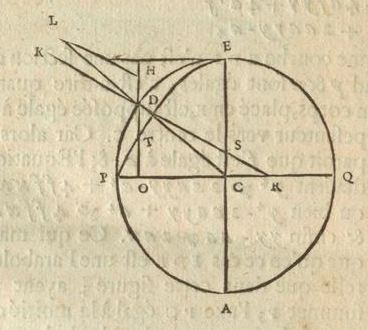
 les autres lignes estant nommées comme devant. Il est certain que l'eau de EC & celle de DC se doivent derechef contrebalancer. Et mesme, cela doit arriver de quelque maniere qu'on conçoive que le canal soit fait, pourvû qu'il aboutisse de part & d'autre à la surface; comme, par ex. s'il alloit par DOCE, ou DOP, ou DCP. Maintenant, la force centrifuge de toute l'eau en CD, est égale à celle de l'eau qui rempliroit le canal OD, supposé de mesme largeur; ce qui se voit facilement par la Mechanique des plans inclinez. Mais comme EC
les autres lignes estant nommées comme devant. Il est certain que l'eau de EC & celle de DC se doivent derechef contrebalancer. Et mesme, cela doit arriver de quelque maniere qu'on conçoive que le canal soit fait, pourvû qu'il aboutisse de part & d'autre à la surface; comme, par ex. s'il alloit par DOCE, ou DOP, ou DCP. Maintenant, la force centrifuge de toute l'eau en CD, est égale à celle de l'eau qui rempliroit le canal OD, supposé de mesme largeur; ce qui se voit facilement par la Mechanique des plans inclinez. Mais comme EC
Laquelle Equation, en supposant ap/n – 4 afyy + 4 a3f + 2 aayy – a4 25) Qui fait voir que la ligne courbe EDP n'est pas une section de Cone, si ce n'est quand p & n sont égales; c'est-à-dire quand la force centrifuge d'un corps, placé en E, est supposée égale à sa pesanteur vers le centre C. Car alors il paroit que f est égale à a; & l'Equation devient y4
25) C'est l'équation trouvée en novembre ou décembre 1687 d'après la p. 401 qui précède. |
| [ 470 ] | [ v ] |
 Parabole 26), telle que dans cette figure; ayant le sommet P; l'axe PC égal à la moitié de CE; & le parametre double de la mesme CE.
Parabole 26), telle que dans cette figure; ayant le sommet P; l'axe PC égal à la moitié de CE; & le parametre double de la mesme CE. De sorte que si la Terre, ayant le diametre EA de la grandeur qu'il est, tournoit, sur son axe PQ, 17 fois plus viste qu'elle ne fait, (car alors la force centrifuge en E seroit égale à la pesanteur vers le centre, par la demonstration qui est dans | 158 | ce Discours) elle auroit la figure du corps que font ces deux demies Paraboles opposées, PEC, QEC, en tournant autour de l'axe PQ. Et on voit que c'est là la plus grande force centrifuge qu'on puisse supposer; par ce que, si on la faisoit plus grande que la pesanteur, les corps placez en E s'envoleroient en l'air.
Hors de ce cas, si dans l'Equation trouvée l'on fait yy |
|
Et mettant d pour ff/a – f, viendra z |
|
D'où je connois que, CO estant x, si la perpendiculaire OT est appellée z; le point T sera dans une Hyperbole dont l'axe adjouté à CE sera 4 d. Et que comme 4 ff à aa, ainsi sera l'axe au parametre; qui sera donc aad/ff, c'est-à-dire a – na/p, en restituant les valeurs de d & de f. Et parce que yy estoit égale à az, il s'ensuit que DO Or cette ligne satisfait aussi à ce que j'ay dit estre requis; sçavoir que menant DR qui luy soit à angles droits, 26) Comparez la p. 393 qui précède. 27) Equation également trouvée plus haut (p. 402). |
| [ 471 ] | [ v ] |
|
la raison | 159 | OR à RC sera composée de la raison de p à n, & de EC à CD, comme cela se peut prouver par le calcul d'Algebre 28). J'ay supposé dans tout ce raisonnement que la pesanteur est la mesme au dedans de la Terre qu'à sa surface; ce qui me paroit fort vraisemblable, non obstant la raison qu'on peut avoir d'en douter, dont je parleray aprés. Mais quand il en seroit autrement 29), cela ne changeroit presque rien à ce qui a esté trouvé de la figure de la Terre: mais bien alors quand la force centrifuge fait une partie considerable de la pesanteur, ou qu'elle luy est égale, comme dans le cas de la figure Parabolique, qui alors deviendroit tout autre. Au reste quand la force centrifuge en E est tres petite à raison de la pesanteur, comme elle est icy sur la Terre, l'Hyperbole ETP, à cause du grand éloignement de son centre, approche fort de la Parabole, & par consequent EDP ne differe guere de l'Ellipse; ni guere aussi du cercle, parce que EC alors ne surpasse CP que de fort peu; comme il a esté trouvé peu devant, que cet exces n'est que 1/578 de EC, demidiametre de la Terre. Monsieur Newton trouve 1/231 de EC, & que ainsi la figure de la Terre differe bien plus de la spherique; se servant en cela d'une toute autre supputation. que je n'examineray pas icy, parce qu'aussi bien je ne suis pas d'accord d'un Principe qu'il suppose dans ce calcul & ailleurs; qui est, que toutes les petites parties, qu'on peut imaginer dans deux ou plusieurs differents corps, s'attirent ou tendent à s'approcher mutuellement. Ce que je ne sçaurois admettre, parce que je crois voir clairement, que la cause d'une telle attraction n'est point explicable par aucun principe de Mechanique, ni des regles du mouvement. comme je ne suis pas persuadé non plus de la necessité de l'attraction mutuelle des corps entiers; ayant fait voir que, quand il n'y auroit point de Terre, les corps ne laisseroient pas, par ce qu'on appelle leur pesanteur, de tendre vers un centre. 28) L'équation de la courbe [ ... ]. Evidemment, on peut aussi commencer le calcul en se servant de la méthode de Huuygens (T. XX, p. 243 et suiv.) pour trouver la soustangente. 29) Huygens veut probablement dire: quand la pesanteur, au dedans de la terre, ne serait pas tout-à-fait constante. |
| [ 472 ] | [ v ] |
|
| 160 | Je n'ay donc rien contre la Vis Centripeta, comme Mr. Newton l'appelle, par la quelle il fait peser les Planetes vers le Soleil, & la Lune vers la Terre, mais j'en demeure d'accord sans difficulté: parce que non seulement on sçait par experience qu'il y a une telle maniere d'attraction ou d'impulsion dans la nature, mais qu'aussi elle s'explique par les loix du mouvement, comme on a vû dans ce que j'ay écrit cy dessus de la pesanteur. Car rien n'empêche que la cause, de cette Vis Centripeta vers le Soleil, ne soit semblable à celle qui pousse les corps, qu'on appelle pesants, à descendre vers la Terre. Il y avoit long temps que je m'estois imaginé, que la figure spherique du Soleil pouvoit estre produite de mesme que celle qui, selon moy, produit la sphericité de la Terre 30); mais je n'avois point etendu l'action de la pesanteur à de si grandes distances, comme du Soleil aux Planetes, ni de la Terre à la Lune; parce que les Tourbillons de Mr. Des Cartes, qui m'avoient autrefois paru fort vraisemblables, & que j'avois encore dans l'esprit, venoient à la traverse. Je n'avois pas pensé non plus à cette diminution reglée de la pesanteur, sçavoir qu'elle estoit en raison reciproque des quarrez des distances du centre: qui est une nouvelle & fort remarquable proprieté de la pesanteur, dont il vaut bien la peine de chercher la raison. Mais voyant maintenant par les demonstrations de Mr. Newton, qu'en supposant une telle pesanteur vers le Soleil, & qui diminue suivant la dite proportion, elle contrebalance si bien les forces centrifuges des Planetes, & produit justement l'effet du mouvement Elliptique, que Kepler avoit deviné, & verifié par les observations, je ne puis guere douter que ces Hypotheses touchant la pesanteur ne soient vrayes, ni que le Systeme de Mr. Newton, autant qu'il est fondé la dessus, ne le soit de mesme. Qui doit paroitre d'autant plus probable, qu'on y trouve la solution de plusieurs difficultez, qui faisoient de la peine dans les Tourbillons | 161 | supposez de Des Cartes. On voit maintenant comment les excentricitez des Planetes peuvent demeurer constamment les mesmes: pourquoy les plans de leurs Orbes ne s'unissent point, mais gardent leurs differentes inclinaisons à l'égard du plan de l'Ecliptique, & pourquoy les plans de tous ces Orbes passent necessairement par le Soleil 31). Comment les mouvemens des Planetes peuvent s'accelerer & se ralentir par les degrez qu'on y observe; qui malaisement pouvoient estre tels, si elles nageoient dans un Tourbillon autour du Soleil 32).
30) Il semble qu'ici Huygens attribue la forme sphérique — ou presque sphérique — de la terre aux mouvements tourbillonnaires de la matière extérieure aussi bien qu'intérieure. Ailleurs il ne parle que de cette dernière (voyez les p. 497 - 498 qui suivent). 31) Voyez sur cette dernière question la note 10 de la p. 350 qui précède. 32) Dans les "Pensees meslees", au § 16, donc en 1686 (ou peut-être en 1687 puisque la phrase a été ajoutée après coup) Huygens ne se montrait pas encore convaincu de l'imppossibilité ou du moins de la grande difficulté, pour employer un terme moins fort, qu'il y aurait à vouloir expliquer par certaines propriétés des tourbillons les accélérations et ralentissements kepleriens des planètes. |
| [ 473 ] | [ v ] |
|
On y voit enfin comment les Cometes peuvent traverser nostre Systeme. Car depuis qu'on sçait qu'elles entrent souvent dans la region des Planetes, on avoit de la peine à concevoir comment elles pouvoient quelquefois aller d'un mouvement contraire à celuy du Tourbillon, qui avoit assez de force pour emporter les Planetes 33). Mais, par la doctrine de Mr. Newton, ce scrupule est encore osté; puisque rien n'y empêche que les Cometes ne parcourent des chemins Elliptiques autour du Soleil, comme les Planetes; mais des chemins plus étendus, & de figure plus differente de la circulaire; & qu'ainsi ces corps n'aient leurs retours periodiques, comme quelques Philosophes & Astronomes anciens & modernes se l'estoient imaginé. Il y a seulement cette difficulté, que Mr. Newton, en rejettant les Tourbillons de Des Cartes, veut que les espaces celestes ne contienent qu'une matiere fort rare, afin que les Planetes & les Cometes rencontrent d'autant moins d'obstacle en leur cours. Laquelle rareté estant posée, il ne semble pas possible d'expliquer ni l'action de la Pesanteur, ni celle de la Lumiere, du moins par les voies dont je me suis servi. Pour examiner donc ce point, je dis que la matiere etherée peut estre censée rare de deux manieres, sçavoir ou que ses particules soient distantes entre elles, avec beaucoup de vuide entre deux; ou quelles se touchent, mais que le tissu de chacune soit rare, & | 162 | entre-meslé de beaucoup de petits espaces vuides. Pour ce qui est du vuide, je l'admets sans difficulté, & mesme je le crois necessaire pour le mouvement des petits corpuscules entre eux. n'estant point du sentiment de Mr. Des Cartes, qui veut que la seule étendue fasse l'essence du corps; mais y adjoutant encore la dureté parfaite, qui le rende inpenetrable, & incapable d'estre rompu ni écorné. Cependant à considerer la rareté de la premiere maniere, je ne vois pas comment alors on pourroit rendre raison de la Pesanteur: & quant à la Lumiere, il me semble entierement impossible, avec de tels vuides, d'expliquer sa prodigieuse vitesse, qui doit estre six cent mille fois plus grande que celle du Son, suivant la demonstration de Mr. Romer, que j'ay raportée au Traité de la Lumiere [p. 7]. C'est pourquoy je tiens qu'une telle rareté ne sçauroit convenir aux espaces celestes. Il y a plus d'apparence de la concevoir de l'autre façon; parce que les particules s'y peuvent toucher, comme je les ay supposées au dit Traité [14], & toutefois, à cause de la legereté de leur tissu, resister fort peu au mouvement des Planetes. Car que sçait on jusqu'où la nature peut aller à composer des corps durs, avec peu de matiere; sur tout, si des particules tres menues & deliées, ou mesme creuses 34), peuvent estre infiniment fortes. 33) Comparez la note 1 de la p. 288 du T. XIX [<]. Il est vrai que malgré cette "peine à concevoir" Huygens avait encore tâché en 1686 (§ 16 de la p. 353 qui précède) de rendre plausible le mouvement assez libre d'une comète au travers d'un vortex deferens. 34) Il n'est pas question ici de particules parfaitement creuses renfermant, pour ainsi dire, des chambres sans fenêtres; comparez ce que Huygens disait quelques années plus tôt (p. 381 qui précède) sur l'impossibilité de l'existence de particules creuses ainsi conçues, et consultez aussi le troisième alinéa de la p. 458 qui précède. |
| [ 474 ] | [ v ] |
|
Mais je crois que, sans considerer la rareté, la grande agitation de la matiere etherée, peut contribuer beaucoup à sa penetrabilité. Car si le petit mouvement des particules de l'eau la rend liquide, & de beaucoup moindre resistence, à l'égard des corps qui nagent dedans, que n'est le sable ou quelque poudre tres fine; ne faut il pas qu'une matiere plus subtile, & infiniment plus agitée, soit aussi d'autant plus aisée à penetrer? Quoyqu'il en soit, nous voions que la nature ne manque pas d'industrie, pour faire qu'il y ait des espaces, dans lesquels les corps se meuvent avec tres peu de resistence; car cela paroit | 163 | par ce que nos mains sentent dans l'air, & encore plus par les experiences qu'on fait dans les vaisseaux de verre, dont on a tiré tout l'air; òu la plume la plus legere, descend avec la mesme vitesse qu'une balle de plomb. Que si on vouloit soutenir que cela procede de la grand rareté de la matiere qui reste dans ce vuide d'air; j'alleguerois au contraire qu'on y aperçoit l'effet d'une matiere qui pese fort considerablement 35), comme on a vû dans l'experience cy dessus raportée. Quant au raisonnement de Mr. Newton dans la Prop. 6. [Fr.] du Livre 3. pour prouver l'extreme rareté de l'ether: sçavoir que les pesanteurs des corps sont comme les quantitez de la matiere qu'ils contienent; & que, cela estant, si les espaces de l'air ou de l'éther estoient aussi pleins de matiere que l'or & l'argent, ces metaux n'y descendroient pas; parce qu'un corps solide, n'ayant pas une plus grande pesanteur specifique qu'un fluide, n'y sçauroit enfoncer. je dis que je suis d'accord que les pesanteurs des corps suivent les quantitez de leur matiere; & je l'ay mesme demontré dans ce present Discours. Mais j'ay aussi fait voir, qu'à ces corps que nous appellons pesants, la pesanteur peut bien estre imprimée par la force centrifuge d'une matiere, qui ne pese point elle mesme vers le centre de la Terre, à cause de son mouvement circulaire & tres rapide; mais qui tend à s'en éloigner. Cette matiere donc peut fort bien remplir tout l'espace autour de la Terre, que d'autres corpuscules n'occupent point, sans que cela empesche la descente des corps qu'on appelle pesants; estant au contraire la seule cause qui les y oblige. Ce seroit autre chose si on supposoit que la pesanteur fust une qualité inherente de la matiere corporelle. Mais c'est à quoy je ne crois pas que Mr. Newton consente, parce qu'une telle hypothese nous eloigneroit fort des principes Mathematiques ou Mechaniques. Il me dira peutestre, que, quand on m'auroit accordé | 164 | que la matiere etherée consiste en des particules qui se touchent, pour transmettre la lumiere; on ne verroit pas 35) Nous avons déjà observé plus haut (p. 380) que Huygens n'ose pas toujours identifier avec l'éther luminifère la matière fort pesante qu'il croyait avoir découverte par l'expérience du fluide qui ne veut pas descendre (T. XIX, p. 214 - 215), comme il le fait dans ses considérations sur les aimants (T. XIX, p. 560 et 585 ). |
| [ 475 ] | [ v ] |
|
pourtant qu'elle observeroit cette regle de ne s'étendre qu'en ligne droite, comme elle fait; parce que cela est contre sa Propos. 42. [Fr.] du 2 Livre. qui dit que le mouvement, qui se repand dans une matiere fluide, ne s'etend pas seulement tout droit depuis son origine, apres avoir passé par quelque ouverture, mais qu'il s'ecarte aussi à costé. A quoy je repons par avance, que ce que j'ay allegué, pour prouver que la lumiere (horsmis en la reflexion ou en la refraction) ne s'etend que directement, ne laisse pas de subsister non obstant la dite Proposition. Parce que je ne nie pas que, quand le Soleil luit à travers une fenestre, il ne se repande du mouvement à costé de l'espace eclairé; mais je dis que ces ondes detournées sont trop foibles pour produire de la lumiere. Et quoyqu'il veuille que l'emanation du Son prouve que ces epanchemens à costé sont sensibles, je tiens pour assuré qu'elle prouve plustost le contraire. Par ce que si le Son, ayant passé par une ouverture, s'etendoit aussi à costé, comme veut Mr. Newton, il ne garderoit pas si exactement, dans l'Echo, l'égalité des angles d'incidence & de reflexion; en sorte que quand on est placè en un lieu, d'où il ne peut point tomber de perpendiculaire sur le plan reflechissant d'un mur un peu eloigné, on n'entend point repondre l'Echo au bruit qu'on fait en ce lieu, comme je l'ay experimenté tres souvent. Je ne doute pas aussi, que l'experience qu'il apporte du Son, qu'on entendroit non obstant une maison interposée, ne se trouvast tout autre, pourvû que cette maison fust placée au milieu de quelque grande eau, ou en sorte qu'il n'y eust rien autour, qui pust renvoier quelque parcelle du Son par reflexion. Et pour ce qu'il dit, qu'en quelque endroit qu'on soit dans une chambre, dont la fenestre est ouverte, on y entend le Son de dehors, non pas par la reflexion des murailles, mais venant | 165 | directement de la fenétre; on voit combien il est facile de s'y abuser, à cause de la multitude des reflexions reïterées, qui se font comme dans un instant; de sorte que le Son, qui s'entend comme venant immediatement de la fenétre ouverte, en peut venir, ou des endroits fort proches, aprés une double reflexion. J'avouë donc, que pour ce qui est des ondulations ou cercles qui se font à la surface de l'eau, la chose se passe à peu pres comme l'assure Mr. Newton: c'est à dire qu'une onde, aprés avoir passé l'ouverture, se dilate en suite d'un costé & d'autre, & toutefois plus foiblement là que dans le milieu. Mais pour le Son, je dis que ces emanations par les costez, sont presque insensibles à l'oreille: & qu'en ce qui est de la lumiere, elles ne font point d'effet du tout sur les yeux 36). J'ay crû devoir aller au devant de ces objections que pouvoit suggerer le Livre de Mr. Newton, sçachant la grande estime qu'on fait de cet ouvrage, & avec raison; puis qu'on ne sçauroit rien voir de plus sçavant en ces matieres, ni qui temoigne une 36) Dans sa lettre d'avril 1694 à de Beyrie (T. X. p. 605) Fatio de Duillier écrit à propos de ce passage: "Mr. Newton se rend à ce raisonnement de Mr. Hugens". |
| [ 476 ] | [ v ] |
|
plus grande penetration d'esprit. Il me reste encore deux choses à remarquer dans son Systeme, qui me semblent fort belles, & qui me donneront occasion de faire quelques reflexion. Aprés quoy j'adjouteray ce que j'ay trouvé parmi mes papiers touchant le mouvement des corps à travers l'air, ou autre milieu qui resiste; duquel mouvement il traite au long dans le livre 2. On a vû comment dans le Systeme de Mr. Newton les pesanteurs, tant des Planetes vers le Soleil, que des Satellites vers leurs Planetes, sont supposées en raison double reciproque de leurs distances du centre de leurs Orbes. Ce qui se confirme admirablement par ce qu'il demontre touchant la Lune; sçavoir que sa force centrifuge, que luy donne son mouvement, égale precisement sa pesanteur vers la Terre, & qu'ainsi ces deux forces contraires la tienent suspendue là où elle est. Car la | 166 | distance d'icy à la Lune estant de 60 demidiametres de la Terre, & partant la pesanteur, dans sa region, 1/3600 de celle que nous sentons; il faloit que la force centrifuge d'un corps, qui se mouvroit comme la Lune, égalast de mesme 1/3600 du poids qu'il auroit à la surface de la Terre. Ce qui se trouve effectivement ainsi, & le calcul s'en peut faire aisément, puis qu'on sçait desja que la force centrifuge sous l'Equateur est 1/289 de nostre pesanteur icy bas. Mais puisque cet exemple de la Lune prouve si bien la diminution du poids, suivant la raison reciproque des quarrez des distances du centre de la Terre; on pourroit douter s'il n'y auroit pas aux Pendules une autre inégalité, outre celle qui estoit causée par le mouvement journalier. Car si la Terre n'est pas spherique, mais assez pres spheroïde, & qu'un point sous l'Equateur est plus eloigné du centre, que n'est un point sous le Pole, dans la raison de 578 à 577, comme il a esté dit cy-devant; les pesanteurs estant en ces endroits en raison contraire des quarrez de ces distances, il faudroit aussi que le pendule sous l'Equateur fust plus court, que celuy dessous le Pole, dans cette mesme raison contraire 36.). C'est à dire que ces pendules seroient comme 288 à 289; ou que le pendule sous l'Equateur seroit plus court de 1/289 de ce qu'il seroit sous le Pole. Qui est justement la mesme difference, qui provenoit cy dessus du mouvement journalier, ou de la force centrifuge. De sorte qu'une Horloge, avec la mesme longueur de pendule, iroit plus lentement sous l'Equateur que sous le Pole, du double de ce qu'elle retardoit par le mouvement de la Terre; & ainsi cette difference journaliere sous l'Equateur seroit de pres de 5 minutes. Et sous les autres paralleles, on la trouveroit par tout plus que double de ce qu'elle y estoit auparavant. Mais je doute fort que l'experience confirme cette grande variation 37), puisque j'ay vû que, dans le voiage 36.) Telle n'est pas précisement l'opinion de Newton, comme nous l'avons remarqué aussi vers la fin de l'Avertissement [440]. 37) Voyez, outre l'Avertissement, notre remarque dans la Partie H de la p. 422 qui précède, où nous avons cité ce passage du Discours. |
| [ 477 ] | [ v ] |
|
dont j'ay fait mention, la seule premiere équation suffit, & que la plus que double mettroit, vers | 167 | le milieu du chemin, trop de difference entre la route du vaisseau, calculée sur le Pendule, & celle qu'il tenoit par l'Estime des Pilotes. Et pour rendre raison pourquoy la seconde variation n'auroit point lieu, je dis qu'il ne seroit pas étrange si la pesanteur, prés de la surface de la Terre, ne suivoit pas precisement, ainsi que dans les regions plus élevées, la diminution que font les differentes distances du centre 38); parce qu'il se peut que le mouvement de la matiere qui cause la pesanteur, soit aucunement alteré dans la proximité de la Terre. comme il l'est apparemment au dedans: puisque sans cela il faudroit dire que la pesanteur, en allant vers le centre, augmenteroit â l'infini; ce qui n'est point vraisemblable. Au contraire, selon Mr. Newton, la pesanteur au dedans de la Terre diminue suivant que les corps approchent du centre; mais il se sert à le prouver de son principe, dont j'ay dit que je ne suis pas d'accord. Ce qui me reste à remarquer touchant son Systeme, & qui m'a fort plû, c'est qu'il trouve moyen, en supposant la distance d'icy au Soleil connue, de definir quelle est la pesanteur que sentiroient les habitans de Saturne & de Jupiter, comparée à la nostre icy sur la Terre, & quelle encore est sa mesure à la surface du Soleil 39). Choses qui d'abord semblent bien éloignées de nostre connoissance; & qui pourtant sont des consequences des principes que j'ay raportez peu devant. Cette determination a lieu dans les Planetes qui ont un ou plusieurs Satellites, parce que les temps periodiques de ceux cy, & leur distances des Planetes qu'ils accompagnent, doivent entrer dans le calcul. Par lequel Mr. Newton trouve les pesanteurs aux surfaces du Soleil, de Jupiter, de Saturne, & de la Terre, dans la raison de ces nombres, 10000, 804½, 536, 805½. Il est vray qu'il y a quelque incertitude à cause de la distance du Soleil, qui n'est pas assez bien connuë, & qui a esté prise dans ce calcul d'environ 5000 diametres de la Terre, au | 168 | lieu que, suivant la dimension de Mr. Cassini, elle est environ de 10000, qui approche assez de ce que j'avois autrefois trouvé, par des raisons vraisemblables, dans mon Systeme de Saturne, sçavoir 12000 40). Je differe aussi de quelque chose en ce qui est des diametres des Planetes. De sorte que, par ma supputation, la pesanteur dans Jupiter, à celle que nous avons icy sur la Terre, se trouve comme 13 à 10, au lieu que Mr. Newton les fait égales, ou insensiblement differentes. Mais la pesanteur dans le Soleil, qui, par les nombres qu'on vient de voir, estoit environ 12 fois plus grande que la nostre sur la Terre, je la trouve 26 fois plus grande. D'où s'ensuit 41), en expliquant la pesanteur de la façon que j'ay fait, que la matiere fluide, 38) Comparez ce que nous avons dit dans la Partie A de la p. 416 qui précède. 39) Voyez sur ces calculs les p. 408-412 qui précèdent. 40) Comparez ce que nous avons dit à la p. 348 qui précède. [Systema Saturnium, p. 80 (Fr.).] 41) Voyez la p. 411 qui précède. |
| [ 478 ] | [ v ] |
|
aupres du soleil, doit avoir une vitesse 49 fois plus grande que celle que nous avons trouvée pres de la Terre; qui estoit desià 17 fois plus grande que la vitesse d'un point sous l'Equateur. Voila donc une terrible rapidité; qui m'a fait penser si elle ne pouroit pas bien estre la cause de la lumiere eclatante du Soleil, supposé que la lumiere soit produite comme je l'explique dans ce que j'en ay écrit; sçavoir de ce que les particules Solaires, nageant dans une matiere plus subtile & extremement agitée, frappent contre les particules de l'Ether qui les environnent. Car si l'agitation d'une telle matiere, avec le mouvement qu'elle a icy sur la Terre, peut causer la clarté de la flamme d'une chandelle, ou du Camphre allumé, combien plus grande fera t'elle cette clarté par un mouvement 49 fois plus prompt & plus violent? J'ay vu avec plaisir ce que Mr. Newton écrit touchant les chûtes & les jets des corps pesants dans l'air, ou dans quelqu'autre milieu qui resiste au mouvement; m'estant appliqué autrefois 42) à la mesme recherche. Et puisque cette matiere appartient en partie à celle de la Pesanteur, je crois pouvoir raporter icy ce que j'en decouvris alors. Ce que je ne feray pourtant qu'en abregé | 169 | & sans y joindre les demonstrations; ayant negligé de les achever, parce que cette speculation ne m'a pas semblé assez utile, ni de consequence, à proportion de la difficulté qui s'y rencontre. J'examinay premierement ces mouvemens, en supposant que les forces de la Resistance sont comme les Vitesses des corps, ce qui alors me paroissoit fort vraisemblable. Mais ayant obtenu ce que je cherchois, j'appris presque en mesme temps, par les experiences que nous fîmes à Paris dans l'Academie des Sciences, que la resistance de l'air, & de l'eau, estoit comme les quarrez des vitesses 43). Et la raison est assez aisée à concevoir; parce qu'un corps, allant par exemple avec double vitesse, est rencontré par deux fois autant de particules de l'air ou de l'eau, & avec double celerité. Ainsi je vis ma nouvelle Theorie renversée, ou du moins inutile. Apres quoy je voulus aussi chercher ce qui arrive lors qu'on suppose ce veritable fondement des Resistances; où je vis que la chose estoit beaucoup plus difficile, & sur tout en ce qui regarde la ligne courbe que parcourent les corps jettez obliquement. Dans la premiere supposition, où les resistances sont comme les vitesses, je remarquay que, pour trouver les espaces passez en de certains temps, lors que les corps tombent ou montent perpendiculairement, & pour connoitre les vitesses au bout de ces temps, il y avoit une ligne courbe, que j'avois examinée long temps auparavant, qui estoit la Logarithmique ou la Logistique, car je ne vois pas qu'on luy ait encore donné de nom, quoyque 42) Déjà, et surtout, en 1668; voyez la p. 381 qui précède. 43) Voyez ces expériences aux p. 120-127 du T. XIX. |
| [ 479 ] | [ v ] |
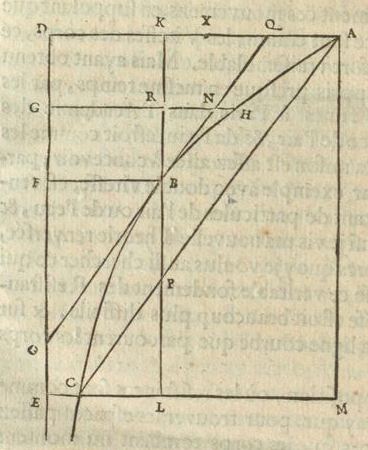
| d'autres l'aient encore considerée cy devant 44). Cette ligne infinie estant ABC, elle a une ligne droite pour Asymptote, comme DE; dans la quelle si on prend des parties égales quelquonques qui se suivent, comme DG, GF, & que l'on tire des points D, G, F, des perpendiculaires jusqu'à la courbe, sçavoir | 170 | DA, GH, FB, ces lignes seront proportionelles continuës. |
|
D'où l'on voit qu'il est aisé de trouver autant de points qu'on veut dans cette courbe; de la quelle je raporteray par apres quelques proprietez qui meritent d'estre considerées. Pour expliquer ce qui est des chûtes des corps, je repete icy premierement ce que j'ay écrit à la fin du Traité du Centre d'Agitation 45): sçavoir qu'un corps, en tombant à travers l'air, augmente continuellement sa vitesse, mais toutefois en sorte qu'il n'en peut jamais exceder, ni mesme atteindre, un certain degré; qui est la vitesse qu'il faudroit à l'air à soufler de bas en haut, pour tenir le corps suspendu sans pouvoir descendre; car alors, la force de l'air contre ce corps, égale sa pesanteur. J'appelle cette vitesse, dans chaque corps, la vitesse Terminale.
44) [...] Leibniz annonce dans une lettre du 8 mars 1673 une dissertation du P. Pardies (mort peu après) sur la linea logarithmica, dont il (P.) avait déjà dit quelques mots dans ses "Elementa Geometriae". Collins fait répondre à Leibniz par Oldenburg, le 6 avril 1673, que cette courbe est déjà bien connue en Angleterre. [... Huygens ..] s'était occupé de la courbe depuis 1661 (T. XIV [429-]) [...]. Huygens ne songe certainement pas à Torricelli (voyez la p. 554 du T. XX); mai voyez ce qu'il dit plus loin (p. 179) sur les considérations auxquelles l' "Opus Geometricum" de 1647 de Gregoire de St. Vincent donna lieu, et aussi ce que nous avons dit sur Kepler à la p. 294 du T. XX. 45) P. 359 du T. XVIII. Huygens parle de la Quatrième Partie de l' "Horologium oscillatorium" de 1673 [p. 156]. |
| [ 480 ] | [ v ] |
|
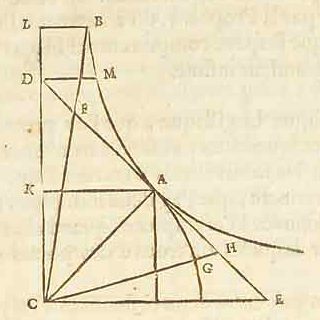
Si donc un corps pesant est jetté perpendiculairement en haut, avec une vitesse dont la raison à la vitesse Terminale soit donnée, par exemple comme de la partie AK à KD dans l'ordonnée AD, perpendiculaire à l'asymptote DE; soit menée KB parallele à cette asymptote, & qu'au point B la courbe soit touchée par la droite BO, qui rencontre DE en O, & DA en Q. Laquelle tangente se trouve en prenant FO, depuis l'ordonnée | 171 | BF, égale à une certaine longueur, qui pour toutes les tangentes est la mesme, & que je definiray dans la suite. Puis soit AC parallele à cette tangente, coupant KB prolongée en P; & du point C, où elle rencontre la courbe, soit tirée CLM, parallele à AD, & coupant KB prolongée, & AM parallele à l'asymptote, aux points L & M. Maintenant le temps que le corps met à monter à la hauteur où il peut arriver, est au temps de sa descente de cette mesme hauteur, comme la ligne KB à BL 46).
Et la hauteur à laquelle il montera dans l'air, à celle où il monteroit sans resistence, comme l'espace ABK au triangle APK 48), ou comme QA à AX, que je suppose estre la moitié d'une troisieme proportionelle aux lignes DK, KA 49). Et sa vitesse, en commençant de monter, à celle qu'il a en retombant à terre, comme ML à LC 50). On trouve de plus, par cette mesme ligne, quelle est la courbe que parcourt un corps jetté obliquement. Car, dans la mesme figure, si l'angle du jet, sur la ligne horizontale, est LMR, avec une vitesse donnée, dont le mouvement en 46) Ceci correspond à la l. 4 d'en bas de la p. 117 du T. XIX: "Tempus autem ascensus ad tempus descensus erit ut CD ad DI". Nous avons dit dans la note 4 de la p. 116 de ce Tome que le calcul des p. 116 - 117 (§ 10) date probablement de 1668. D'ailleurs la même chose se trouve déjà au § 6 (l. 5 - 6 de la p. 111 du T. XIX), ainsi qu'au § 7 (l. 8 de la p. 113 du même Tome) qui sont certainement de 1668. 47) Ceci correspond aux l. 9 - 6 d'en bas de la p. 102 (§ 1) du T. XIX datant de 1668: "Et quam rationem habebit CN ad CE, eam habebit tempus ascensus corporis N [auquel l'air ne résiste pas] ad tempus totius ascensus corporis R". Il est vrai qu'ici il avait été supposé que la vitesse initiale des deux corps montants était la "vitesse terminale", ce qui se traduisait dans la figure par l'égalité des longueurs qui dans la présente Fig. 133 sont désignées par AK et KD. 48) Ceci correspond aux dernières lignes de la p. 103 du T. XIX; même remarque sur les vitesses. 49) On a: espace ABK = AQ x latus rectum (T. XIX, § 5, p. 110, l. 9 - 7 d'en bas). Il faut donc encore démontrer [...]. 50) Ceci correspond au rapport VH : ZX de la l. 8 de la p. 113 (§ 7) de 1668 du T. XIX. |
| [ 481 ] | [ v ] |
|
haut soit à la vitesse Terminale comme AK à KD: soit repetée la construction precedente, & que la droite AS, qui touche la courbe ABC en A, rencontre KB en S. Puis comme SP à PB ainsi soit RL à LT, & sur la base MC soit dressée une figure proportionelle au segment ABCP, en sorte que les paralleles & également distantes de l'asymptote DE, dans l'une & l'autre figure, aient par tout la mesme raison de BP à TL. Ce sera la courbe MTC qui marquera la figure requise du jet 51). Et parce que la hauteur de l'élevation avec resistence, estoit à la hauteur du jet libre, comme QA à AX; si l'on fait que TL ait cette mesme raison à une autre ligne VZ; ce sera la hauteur | 172 | de la Parabole MV que fait ce jet libre, commencé en M |
|
avec la mesme force, & dans la mesme direction MR, qu'avoit l'autre jet. De sorte que si dans l'angle LMR on ajuste YZ perpendiculaire à MC, & égale à la double VZ, on aura le sommet de cette parabole en V au milieu de YZ, & sa demie base ou demie amplitude MZ. Il est à noter que, quel que soit l'angle d'elevation LMR, pourvu que la vitesse verticale demeure la mesme, on trouve icy la mesme amplitude MC. Mais il faut estre averti que ce sont seulement les figures des jets qu'on trouve de cette façon, & 51) C'est la construction des p. 116 - 119 (§§ 10 et 11) du T. XIX. |
| [ 482 ] | [ v ] |
|
non pas les hauteurs & les amplitudes de divers jets comparez ensemble. Car ils doivent tous estre de mesme hauteur, quand la celerité | 173 | verticale est la mesme. C'est pourquoy alors chaque figure de jet, ainsi trouvée, doit estre reduite à une figure proportionelle d'égale hauteur, si on veut sçavoir comment les amplitudes, & les hauteurs des divers jets, sont les unes aux autres. J'adjoute encore icy, que la ligne Logarithmique ne sert pas seulement à trouver les courbes des jets, mais qu'elle est cette courbe elle mesme en un cas, sçavoir quand on jette un corps obliquement en bas, en sorte que ce qu'il y a de descente perpendiculaire, égale la vitesse Terminale 52). Car alors ce corps suivra precisement la courbure d'une telle ligne, en s'approchant tousjours de l'asymptote, sans la pouvoir atteindre. Et ce qui determine l'espece de la ligne, c'est que sa Soutangente, (je nommeray ainsi la ligne FO, qui pour toutes les tangentes est la mesme) sera double de la hauteur à laquelle la vitesse Terminale peut faire monter le corps, sans resistance du milieu 53). Ce sont là les choses que je trouvay en supposant la resistance estre comme la vitesse, mais toute cette Theorie estant, comme j'ay dit, fondée sur un principe, que la nature ne suit point en ce qui est des resistances de l'air & de l'eau, je la negligeay entierement; & ce n'est qu'à l'occasion du Traité de Mr. Newton que je l'ay reprise, pour voir si ce que nous avions cherché par des voies fort differentes, s'accordoit ensemble comme il faloit. Ce qui se trouve ainsi: car la construction pour la ligne du jet, qu'il donne dans la Propos. 4 [Fr.] du 2 Livre, quoyque tout autre que la miene & plus difficile, produit pourtant la mesme courbe, comme cela se peut prouver par demonstration 54). En examinant ce qui arrive dans la vraye 55) hypothese de la Resistance, ce qui est en raison double de la Vitesse, j'avois seulement determiné ce cas particulier, d'un corps 52) La composante verticale v de la vitesse [...]. 53) Le latus rectum [...]. 54) Voyez l'Appendice I qui suit [489], ainsi que la note 35 de la p. 499. 55) Voyez nos observations sur cette expression aux p. 85 - 86 du T. XIX. |
| [ 483 ] | [ v ] |
| jetté en haut avec la vitesse Terminale; sçavoir que le temps de toute son élevation en l'air, est au temps qu'il emploieroit à monter jusqu'où | 174 | il peut sans resistance, comme le Cercle au Quarré qui luy est circonscrit. Et que la hauteur du premier jet est à la hauteur de l'autre, comme l'espace entre une Hyperbole & son asymptote, terminé par deux paralleles à l'autre asymptote qui soient en raison de 2 à 1, au rectangle où parallelogramme de la mesme Hyperbole. C'est-à-dire, comme, dans la figure suivante, l'espace AMDK au quarré AC 56). Je n'avois point recherché les autres cas, qui sont compris universellement dans la Prop. 9 [Fr.], du 2 Livre de Mr. Newton, qui est tresbelle: & ce qui m'en empêcha, ce fut que je ne trouvois point, par la voie que je suivois, la mesure des descentes des corps, si non en supposant la quadrature de certaine Ligne courbe, que je ne sçavois pas qu'elle dependoit de la quadrature de l'Hyperbole. Je reduisis la dimension de l'espace de cette courbe, à une Progression infinie, a + 1/3 a3 + 1/5 a5 + 1/7 a7 &c. Ne sçachant pas que la mesme progression donnoit aussi la mesure du secteur Hyperbolique: ce que j'ay vu depuis, en comparant la demonstration de Mr. Newton avec ce que j'avois trouvé 57). |
|
Mais par ce que cette Progression, pour la mesure de l'Hyperbole, n'a pas encore esté remarquée que je sçache, je veux expliquer icy comment elle y sert. Soit AB une Hyperbole, dont les asymptotes DC, CE fassent un angle droit. le demi axe soit CA, perpendiculaire à DAE qui touche l'Hyperbole; & que ACB soit un Secteur, la ligne CB coupant AD en F. Si on prend maintenant AC ou AD pour l'unité, & que AF soit nommée a, qui est une fraction moindre que l'unité, quand AF, AD sont commensurables; je dis que, comme la somme de la Progression infinie a + 1/3 a3 + 1/5 a5 + 1/7 a7, &c. à 1, ainsi sera le Secteur ACB au triangle ACD. Ou si on mene les perpendiculaires AK, BL sur l'asymptote, on peut dire la mesme chose de l'espace ABLK, qui est égal à ce Secteur, comme on voit aisement par l'égalité des triangles CAK, CBL. De sorte que cette Progression | 175 | pour l'Hyperbole, respond à celle qu'à donné Mr. Leibnits pour le Cercle 58). par laquelle, si le Secteur du Cercle est ACG, ayant pour rayon AC, & que CG coupe AE en H; AH estant nommée
56) Voyez ces résultats aux p. 147 (note 11) et 151 (note 14) du T. XIX. 57) Sur ce sujet on peut consulter e.a. la note 2 de la p. 471 du T. XIX. [note 12, p. 147] 58) Voyez la note 3 de la p. 472 du T. XX ou la note 13 de la p. 535 du T. IX. |
| [ 484 ] | [ v ] |
|
a, & AE égale à 1; la somme de la Progression a – 1/3 a3 + 1/5 a5 – 1/7 a7 &c. est à 1, comme le Secteur ACG au triangle ACE, ou comme l'arc AG à la droite AE. Pour ce qui est de la ligne du jet oblique; s'il suffisoit, dans cette maniere de resistance, de connoitre le mouvement horizontal & le vertical d'un corps, pour en composer le mouvement oblique, ainsi que dans la premiere hyothese, il y auroit moyen de determiner des points par où cette ligne doit passer: & la mesme ligne Logarithmique y seroit utile, estant tournée en sorte que son asymptote fust parallele à l'horizon; & elle mesme seroit derechef la courbe du jet, dans le cas ou j'ay dit qu'elle servoit auparavant. Mais cette composition de mouvement n'ayant point lieu icy; parce que la diminution du mouvement retardé, dans le diagonale d'un rectangle, n'est pas proportionelle aux diminutions par les costez; il est extremement difficile, si non du tout impossible, de resoudre ce Probleme 59). Le mouvement horizontal estant consideré à part, comme d'une boule qui rouleroit sur un plancher uni, a cela de remarquable icy, qu'il doit aller loin à l'infini, non-obstant la resistance | 176 | du milieu, au lieu que, quand la resistance est comme la vitesse, il est borné, & n'atteint jamais un certain terme. Et cette infinité se prouve aisement par la Propos. 5. [Fr.] du 2 Livre du Traité de Mr. Newton, parce que l'espace compris entre l'Hyperbole & ses asymptotes est de grandeur infinie 60).
Es proprietez de la ligne Logistique, que j'ay promis de raporter, & dont quelques unes ont servi à trouver ce que j'ay remarqué touchant les mouvemens à travers l'air, sont les suivantes; outre la premiere, que j'ay desia indiquée, de la proportionalité des ordonnées à l'asymptote, quand elles sont également distantes, par laquelle on trouve des points dans cette ligne.
2. Que les mesmes choses estant posées, & AO 59) Huygens remarqua en 1689 (ou plus tôt) l'impossibilité de la composition du mouvement dans le cas consideré après avoir lu les "Principia" de Newton: voyez les p. 423 - 426 qui précèdent. Voyez aussi sur ce sujet la p. 498 de l'Appendice II qui suit. 60) Voyez la Partie F de la p. 420 qui précède. 61) Voyez l'avant-dernier alinéa datant de 1661, de la p. 402 [462] du T. XIV. |
| [ 485 ] | [ v ] |
|
estant la tangente au point A, laquelle coupe CE, QK, en I & G; les espaces AVE, ADK sont entre eux comme les droites VI, DG 62). 3. Que l'espace compris entre deux ordonnées, est à l'espace infini, qui, depuis la moindre de ces ordonnées, s'étend entre la Logistique & son asymptote, comme la difference | 177 | des mesmes ordonnées est à la moindre. Quand je dis que l'espace infini a une certaine raison à un espace fini, cela signifie qu'il aproche si prés de la grandeur d'un espace donné, qui a cette proportion à l'espace fini, que la difference peut devenir moindre qu'aucun espace donné. Dans la figure precedente l'espace ABQD est à l'espace infini, qui depuis DQ s'étend entre la courbe & l'asymptote, comme KD à DQ 63). 4. Que la Soutangente, comme BO dans la mesme figure, est tousjours d'une mesme longueur, à quelque point de la Logistique que la tangente apartiene 64). 5. Que cette longueur se trouve par approximation, & qu'elle est à la partie de l'asymptote, comprise entre les ordonnées de la raison double, comme 434294481903251804 à 301029995663981195; ou, bien pres, comme 13 à 9 65).
| 178 | 7. Que l'espace infini entre une ordonnée, la Logistique, & son asymptote, du costé que ces deux dernieres vont en s'approchant, est double du triangle que font l'ordonnée, la tangente menée du mesme point que l'ordonnée, & la soutangente. Ainsi, dans la mesme figure, l'espace infini, depuis l'ordonnée BF, est double du triangle BFO 67).
62) T. XIX, p. 110, l. 7 - 8, datant de 1668. 63) Ce théorème 3 résulte immédiatement du théorème 1. 64) La longueur de la soustangente ou "latus rectum" est constante d'après le deuxième alinéa de la p. 463 du T. XIV. 65) Voyez la p. 464 du T. XIV. Nous avons corrigé 3010399... en 3010299... Le rapport 13 à 9 aussi à la p. 108 du T. XIX. 66) T. XIX, p. 110, l. 6 d'en bas. 67) T. XIV, p. 466, quatrième alinéa. |
| [ 486 ] | [ v ] |
|
8. Que l'espace, compris entre deux ordonnées, est égal au rectangle de la soutangente & de la difference des mesmes ordonnées. Ainsi, dans la mesme figure, l'espace ADFB est égal au rectangle de la soutangente FO & de KA 68). 9. Que le solide que fait l'espace infini depuis une ordonnée, en tournant autour de l'asymptote, est sesquialtere du Cone, dont la hauteur est egale à la soutangente, & le demidiametre de la base égal à la mesme ordonnée. Ainsi le solide que fait l'espace infini BFOC, en tournant autour de FO, est sesquialtere du cone que fait le triangle BFO, en tournant autour de la mesme FO 69). 10. Que le solide produit par le mesme espace infini, en tournant autour de l'ordonnée BF, depuis laquelle il commence, est sextuple du cone que fait le triangle BFO, par sa conversion sur BF 70). De laquelle mesure des solides s'ensuit; 11. Que le centre de gravité de l'espace infini, depuis une ordonnée, est distant de cette ordonnée, de la longueur de la soutangente 71).
13. J'avois aussi trouvé que le centre de gravité du premier des dits solides infinis, est distant de sa base, de la moitié de la soutangente 72). 14. Et que le centre de gravité de l'autre solide est distant de sa base infinie, d'une huitieme de son axe 73). 15. On sçait assez que cette ligne Logistique sert à la Quadrature | 179 | de l'Hyperbole, depuis les demonstrations du P. Greg. de St. Vincent, touchant les espaces Hyperboliques compris entre deux ordonnées sur une des asymptotes 74). Et que s'il y a deux tels espaces, dont les ordonnées de l'un soient comme AD à HG dans la derniere figure, & les ordonnées de l'autre comme BF à CE; ces 68) T. XIV, p. 466, cinquième alinéa. 69) T. XIV, p. 467, deuxième alinéa. 70) Huygens a démontré en 1661 (T. XIV, p. 467 - 470) que le centre de gravité de l' "espace infini" BFOC se trouve à une distance ¼ BF de OF et à une distance l de BF, l étant le latus rectum. Suivant le théorème de Guldin le rapport du solide obtenu par la rotation de l'espace considéré autour de BF à celui obtenu par la rotation du même espace autour de OF est donc 4 l/BF. D'autre part le rapport des volumes des cônes obtenus par la rotation du triangle BFO autour des axes BF et OF respectivement est l/BF. Le théorème 10 résulte donc du théorème 9: au lieu de "sesquialtere du cone" on trouve maintenant "sextuple du cone". 71) On voit aux pages citées du T. XIV (note précédente) que le théorème 9 y est en effet antérieur au théorème 12, tandis que le théorème 10 y est en réalité postérieur au théorème 11. 72) En 1661 Huygens avait énoncé ce théorème sans y ajouter la démonstration (T. XIV, p. 471, avant-dernier alinéa). Sa démonstration de 1689 des trouve aux p. 472 - 473 du même Tome. 73) Dernier alinéa de la p. 471 du T. XIV. Nous y avons donné la démonstration dans une note. 74) Voyez ce que nous avons dit sur Gregoire de St. Vincent aux p. 432 - 434 du T. XIV, ainsi qu'au T. XX [voyez p. 574]. |
| [ 487 ] | [ v ] |
|
espaces seront entre eux comme les lignes DG à FE. Mais on n'a point remarqué, que je sçache, que ces mesmes espaces Hyperboliques sont au Parallelogramme de l'Hyperbole (j'appelle ainsi le parallelogramme dont les costez sont les deux ordonnées sur les asymptotes, tirées d'un mesme point de la Section) comme chacune des lignes DG, FE, à la soutangente FO. De sorte que, si le Parallelogramme de l'Hyperbole est supposé de 0,4342944819 parties, chaque espace Hyperbolique, compris entre deux ordonnées à une des asymptotes, sera à ce parallelogramme, comme le Logarithme de la proportion des mesmes ordonnées, c'est-à-dire comme la difference des Logarithmes, des nombres qui expriment la proportion des ordonnées, au nombre 0,4342944819; en prenant des Logarithmes de 10 characteres outre la characteristique 75).
75) [...] la soustangente ou latus rectum de la courbe logarithmique étant désignée par log e; voyez la p. 464 du T. XIV. [...] 0,4342944819 = log e [...] Comparez sur ce sujet les p. 434 - 435 et 474 - 477 du T. XIV. Ce calcul de Huygens est de 1661. |
| [ 488 ] | [ v ] |
|
| 180 | Et d'icy il est aisé de verifier la Quadrature de l'Hyperbole que j'ay donnée dans le Traité de l'Evolution des Lignes Courbes, qui est dans mon Horologium Oscillatorium 76).
76) P. 218 - 221 du T. XVIII [Ned.; 1673, p. 77 - 79], où 0,3622156887 = – log log e, comme nous avons déjà dit au T. XIV. [ Cf. Guido Grandi, Geometrica demonstratio theorematum Hugenianorum circa logisticam (1701), réimprimé dans Christiani Hugenii ... Opera reliqua (1728), voyez T. XIV, p. 473n.] |