No 1017. Christiaan Huygens aan [P. Petit]. [25 mei 1662]. Aanhangsel bij No. 1016. Het concept en een kopie zijn in Leiden, coll. Huygens. A Monsieur Petit, Sur l'Aequation des jours.   Als de zon, in plaats van over de Ecliptica te gaan, altijd de evenaar volgde, en als hij hierop met een gelijkmatige beweging zou voortgaan, deze in dezelfde tijd doorlopend als hij nu de Ecliptica doet (dat wil zeggen in de tijd van een tropisch jaar), is het zeker dat alle dagen van de ene middag tot de andere noodzakelijker­wijze gelijk zouden zijn, en dat elk ervan zou zijn: een hele omloop van de evenaar en nog een deel van de evenaar dat de zon daarop dagelijks vooruit zou gaan, wat zou zijn 59' 8" 20"' — aangezien zijn gemiddelde beweging op de Ecliptica zoveel bedraagt — zodat de tijd van een middelbare dag, en de juiste maat van 24 uur, die is waarin de 360 graden van de evenaar met 59' 8" 20"' voorbijgaan. 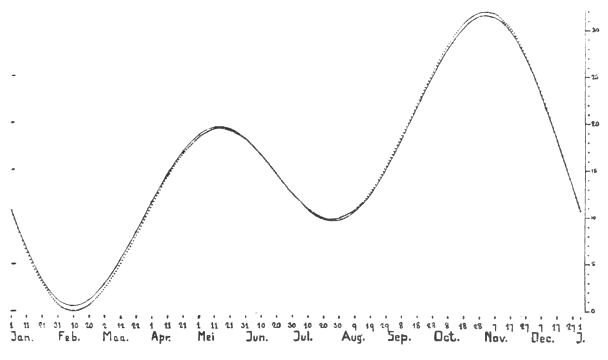Dan zou men helemaal geen tijdvereffening nodig hebben en als het uurwerk eenmaal was afgesteld op de lengte van zulke gemiddelde of middelbare dagen zou het voortdurend overeenstemmen met zonnewijzers. Maar de beweging van de zon is op de Ecliptica, die schuin staat ten opzichte van de evenaar, en deze beweging is bovendien ongelijkmatig door de excentriciteit van de grote baan, en het is door deze twee oorzaken dat men er bijna altijd een verschil in vindt en dat men de juistheid van uurwerken niet door middel van zonnewijzers zou kunnen onderzoeken zonder de genoemde vereffening te gebruiken, waarvoor ik u een tabel 1) heb gegeven met de methode 2) om deze te gebruiken. Maar om u te laten zien wat de grondslag is van de berekening van deze tabel en hoe men deze gemakkelijk opstelt door middel van Efemeriden: laten we bijvoorbeeld nemen dat op 10 april 1660 als de zon op de meridiaan van Parijs staat, op hetzelfde ogenblik het uurwerk, afgesteld op de bovengenoemde middelbare tijd, ook 12 uur aanwijst; en dat ik wil weten of het 10 dagen later, te weten op 20 april, nog 12 uur is op het uurwerk wanneer het dit volgens de zon is, of wat het verschil zal zijn.   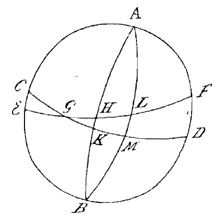Laat van de bol ACBD de polen zijn A en B, de evenaar CD, de ecliptica EF, het teken Aries [Lentepunt] in G. En laat H de plaats van de zon zijn op het middaguur van 10 april. H is dan volgens de Efemeriden van Eichstadt op 21° 20' 45" van [Aries]*), waarvan de rechte klimming   1)  Zie het stuk No. 979.     2)  Zie het stuk No. 978 [Ned.].   [ *)  Zie Ephemeridum novarum et motuum coelestium ab anno M.DC.LI. Ad M.DC.LXV. pars tertia, Amst. 1644, p. 270 (onderste regel): 10 april nieuwe stijl en p. 272: 20 april N.St.]

[ 139 ]

GK is 19° 42', en het punt K is tegelijkertijd met H op de meridiaan. De 20e zal de zon op het middaguur, volgens dezelfde Efemeriden, aangekomen zijn bij 1° 5' 15" van [Taurus], dat is L, en zijn rechte klimming GM zal zijn 28° 56'. En het zal middag zijn wanneer het punt L van de ecliptica en tegelijk het punt M van de evenaar op de meridiaan van Parijs liggen, zodat de duur van de ware zonnedagen [jours apparents] tussen het middaguur van 10 april en het middaguur van de 20e van dezelfde maand bedraagt: 10 hele omwentelingen van de evenaar en nog de boog KM. Als nu de boog KM, die te vinden is door de rechte klimming GK af te trekken van GM, zou zijn 10 maal 59' 8" 20"' of 9. 51' 11" 3), dan zou het zijn alsof de zon op de evenaar was voortgegaan en met zijn gemiddelde beweging, en bijgevolg zou de tijd tussen de twee genoemde middaguren gelijk zijn aan 10 dagen van de gemiddelde tijd, volgens wat ik in het begin gezegd heb. Maar de boog KM is hier maar 9° 14', zodat het verschil 37' is. En bijgevolg zal de plaats van de zon M op de meridiaan van Parijs zijn aangekomen voordat het uurwerk het middaguur aanwijst, en het tijdverschil zal zoveel zijn als voor de genoemde [37'] nodig is om langs de meridiaan te gaan, dat wil zeggen 2 minuten en 28 seconden, want volgens de verhoudingsregel geldt: aangezien de 360 graden en 59' 8" 20"' van de evenaar (met weglating van die 59' 8" 20"' omdat ze niet in aanmerking komen) voorbijgaan in 24 uur, zullen de 37' 0 voorbijgaan in 2' 28" 5. Deze minuten en seconden zijn dus de vereffening die moet worden afgetrokken van de ware zonnetijd [temps apparent] om de gemiddelde tijd van 20 april 1660 te krijgen, wanneer men het middaguur van de 10e dag van dezelfde april heeft gesteld als Epoche of gemeenschappelijk begin van beide tijden. En volgens deze methode kan men voor dezelfde epoche de vereffening berekenen die past bij alle dagen van het jaar, om daarmee een tabel op te stellen.   Nu moet men weten dat de getallen van deze tabel, die als epoche hebben de bovengenoemde 10e april, anders zouden zijn dan die van de tabel die u van mij hebt, die 10 februari als Epoche heeft, maar de vereffeningen die men uit beide zou halen zouden inderdaad geheel dezelfde zijn. Zoals wanneer ik met deze laatste wil onderzoeken hoeveel het uurwerk van de zon moet verschillen op het middaguur van 20 april, als het daarmee in overeenstemming is gebracht op het middaguur van 10 april, dan moet volgens de regel, die ik met de tabel heb gegeven, van het getal dat hoort bij 20 april (dat is 16' 34") afgetrokken worden het getal dat hoort bij 10 april (dat is 14' 6"), waarvan overblijft 2' 28", de tijd dat het middaguur van de ware zon zal voorlopen op dat van het uurwerk, omdat het getal van 20 april groter is dan dat van de 10e. Waarbij u ziet dat het dezelfde vereffening is als die we hierboven hebben gevonden. Het doet er niet toe op welke Epoche de getallen van de Tabel betrekking hebben, aangezien er noodzakelijk dezelfde vereffeningen uit voortkomen.   3)  Lees: 9° 51' 23".

[ 140 ]

Ik heb evenwel in de mijne 10 februari als Epoche genomen (ik zou ook 1 november kunnen nemen) omdat het met een andere dag als begin nodig was geweest in de tabel onderscheid te maken tussen positieve en negatieve vereffeningen, wat het gebruik ervan minder makkelijk had gemaakt. Hij zal gedurende vrij veel jaren zonder noemenswaardige fout kunnen dienen, omdat de verandering van het apogeum van de zon, die als enige hem ongeldig kan maken, zeer langzaam is, te weten ongeveer 1 graad in 60 jaar. Overigens is deze manier van vereffenen niet anders dan die welke Ptolemaeus ons heeft geleerd en na hem Copernicus en verscheidene anderen, om een tijdsduur van de ware zonnetijd te vergelijken met de gelijkmatige tijd [temps egal], en het is zeker de enige en betrouwbare manier.   Sommigen hebben echter bedacht, zoals onze vriend de heer Boulliau in zijn Astronomia Philolaica 4), dat er een vereffening nodig was om het moment van de ware zonnetijd te herleiden tot de gemiddelde tijd, en zonder acht te slaan op de Epoche willen zij dat bij elke dag van het jaar een bepaalde vereffening past, en zij zouden het daarom vreemd vinden dat de ene tabel andere getallen zou hebben dan de andere. Maar hun zogenaamde vereffening is zonder enige grondslag en betekent niets, want van welk moment men ook wil kan men beginnen de gelijkmatige tijd en de ware zonnetijd te rekenen als vanaf een gemeenschappelijk begin, en ze kunnen pas na enige tijd van elkaar verschillen. Zo hebben we net gezien dat de 10 dagen van de ware zonnetijd vanaf het middaguur van 10 april tot het middaguur van 20 april korter zijn dan 10 dagen van de gelijkmatige of middelbare tijd; maar wie zou op het middaguur van de ware zonnetijd van 10 april vragen hoe lang het nog duurt tot het middaguur van de gemiddelde tijd, of hoe lang het al geleden is, ik zou zeggen dat de vraag belachelijk is, tenzij hij acht slaat op een of andere epoche daarvoor, waar men veronderstelt dat de tijdrekening van gemiddelde en ware zonnetijd is begonnen. En al naar gelang men deze epoche stelt zal het middaguur van de gemiddelde tijd komen na of voorlopen op het middaguur van de ware zonnetijd, of precies op hetzelfde tijdstip vallen.   Alvorens te eindigen zal ik u hier nog de opmerkingen zeggen die men kan maken als men er in de vereffeningstabel op let, hoe de getallen erin toenemen en afnemen. Ten eerste, dat de gemiddelde of middelbare lengte van de ware zonnedagen vier keer per jaar voorkomt, te weten omtrent 10 februari, 15 mei, 25 juli en 1 november, wat blijkt omdat als men een van die dagen als epoche neemt, er de volgende 2 of 3 dagen geen of en heel kleine vereffening te maken is. Hierin hebben sommigen zich echter vergist, gelovend dat deze gemiddelde waarde van dagen slechts twee keer per jaar voorkomt.   Vanaf 10 februari tot 15 mei zijn de ware zonnedagen elk korter dan de middelbare, en de kortste is omtrent de laatste dag van maart.   Daarentegen zijn vanaf 15 mei tot 25 juli de ware zonnedagen elk langer dan de middelbare dagen en het langst omtrent 20 juni.   4)  Het werk aangehaald in brief No. 156, noot 7 [T. I, p. 230].   [ Onderstaande figuur is toegevoegd.]

[ 141 ]

Vanaf 25 juli tot 1 november zijn weer de ware zonnedagen korter dan de middelbare, en het kortst omtrent 18 september.   En daarentegen overtreffen de ware zonnedagen de middelbare van 1 november tot 10 februari, en de langste zijn omtrent 24 december, die ook de langste van het hele jaar zijn, 31 seconden langer dan een middelbare dag.   Zo zal een uurwerk dat op het middaguur van 10 februari is gelijkgezet met de zon, op 1 november aanwijzen 11 uur 28' 5" wanneer de zon al op de meridiaan is; wat laat zien dat de ware zonnedagen van deze periode niet gelijk zijn aan evenveel middelbare dagen, maar dat ze 31' 55" korter zijn. Maar als het uurwerk op 1 november met de zon is gelijkgezet, zal het op 10 februari aanwijzen 31' 55" na het middaguur wanneer de zon het middaguur aangeeft; waaruit volgt dat de ware zonnedagen van 1 november tot 10 februari 31' 55" langer zijn dan evenveel middelbare dagen.   Ik zou hierbij nog kunnen opmerken de fout van Ptolemaeus, Copernicus en anderen die hen volgen, die, kijkend naar die twee tijdstippen tussen welke het verschil van de ware en middelbare zonnedagen het grootst is, en overwegend dat de ware zonnedagen van de laatste periode de middelbare evenveel overtreffen als de ware zonnedagen van de eerste periode erdoor worden overtroffen (want bij beide is het verschil 31' 55"), hieruit concluderen dat dus de ware zonnedagen van de laatste periode de ware zonnedagen van de eerste periode overtreffen met tweemaal 31' 55", dat maakt een uur en 3' 50". Wat mijns inziens geheel buiten de rede is, en ik kan niet bedenken op welke manier zij de dagen van de laatste periode kunnen vergelijken met die van de eerste, waarvan er veel minder zijn. De gevolgtrekking die ze eruit maken is ook heel onjuist, te weten dat men met verwaarlozing van de tijdvereffening zich soms zou kunnen misrekenen bij de beweging van de maan met meer dan een halve graad, daar in de genoemde tijd van een uur en 3' 50" de gemiddelde beweging ervan ongeveer 34' is.   Ik zeg dat zij zich hierin met de helft vergissen, aangezien de tijdvereffening slechts gaat tot 31' 55", zodat er in de plaats van de maan slechts een fout kan zijn van ongeveer 17', welke in elk geval belangrijk genoeg is om het gebruik van de vereffening noodzakelijk te maken.   Alvorens te eindigen 5) zal ik u zeggen dat mijn tabel die u hebt niet voor altijd kan dienen, maar alleen voor zo'n 100 jaar vanaf nu zonder opmerkenswaardige fout, en dat men dientengevolge hiermee ook niet een periode van ware zonnetijd van verscheidene eeuwen kan herleiden tot middelbare tijd, zoals vereist wordt bij de berekening van de maanbeweging wanneer men veronderstelt dat de Epoche ver in het verleden is.   De oorzaak zit in de verandering van het aphelium van de zon, dat langzamerhand voortgaat op de Ecliptica, hoewel met een zeer trage beweging van ongeveer een graad in 60 jaar. In deze lange perioden moet dus gebruik gemaakt worden van de regel die Ptolemaeus heeft gegeven, die heel goed is en geen andere grondslag heeft dan die van de berekening van onze tabel.   5)  Het concept dat volgt staat op een apart blad.

[ 142 ]

Ik zal hier niet zeggen hoe deze toegepast moet worden. U zult gemakkelijk begrijpen hoe u deze moet gebruiken bij de berekening van de Maan, want u hoeft alleen de periode van ware zonnetijd tussen de Epoche en het gegeven moment te herleiden tot middelbare tijd.