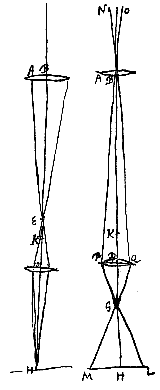
Plat oppervlak
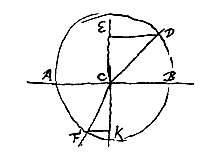 3 Inleiding: Breking van lichtstralen volgens waarnemers en onderzoekers in Oudheid, Middeleeuwen, en recenter. Een beginstuk is van ca. 1662, met Snellius als ontdekker van de brekingswet. Er is een snelle methode om de brekingsindex te bepalen.
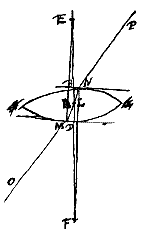
3 Inleiding: Breking van lichtstralen volgens waarnemers en onderzoekers in Oudheid, Middeleeuwen, en recenter. Een beginstuk is van ca. 1662, met Snellius als ontdekker van de brekingswet. Er is een snelle methode om de brekingsindex te bepalen.Hiernaast: de constante ED / FK, in onze notatie: sin i / sin r = n.
13 Voorstel 1: Gegeven een oppervlak van een doorschijnend lichaam, een straal, en de gebroken straal. De verlengden geven de situatie als de lucht en het dichtere medium van plaats wisselen.
15 Voorstel 2: De brekingsindex als verhouding van twee zijden van één driehoek, bij breking naar de normaal toe.
17 Voorstel 3: Idem, bij breking van de normaal af.
17 Opmerking: In het vervolg is de convergentie (of divergentie) niet perfect naar (of vanuit) één punt.
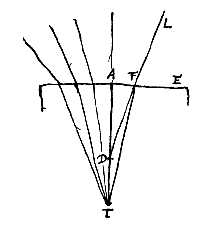 19 Voorstel 4: Gegeven een plat oppervlak van een doorschijnend lichaam, en een punt hierin waar naartoe stralen van buiten convergeren. Te vinden het convergentiepunt van de gebroken stralen.
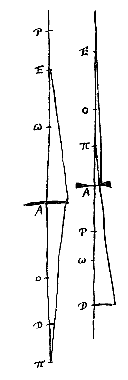
19 Voorstel 4: Gegeven een plat oppervlak van een doorschijnend lichaam, en een punt hierin waar naartoe stralen van buiten convergeren. Te vinden het convergentiepunt van de gebroken stralen.
Hiernaast: T, met TA / AD = n.
23 Voorstel 5: Idem, met een punt erbuiten vanwaar stralen divergerend invallen. Te vinden het divergentiepunt van de gebroken stralen.
25 Voorstel 6: Idem, met een punt hierin vanwaar stralen divergerend invallen. Te vinden het divergentiepunt van de gebroken stralen.
27 Voorstel 7: Idem, met een punt erbuiten waarnaar stralen binnen het lichaam convergeren. Te vinden het convergentiepunt van de gebroken stralen.
Boloppervlak
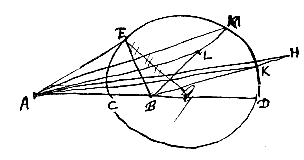
31 Hulpstelling:
Op AB ligt C, en op het verlengde D, zó dat
AD : DB = AC : CB. Nu zal gelden:
AE : EB = AC : CB, als E op de cirkel met middellijn CD ligt.
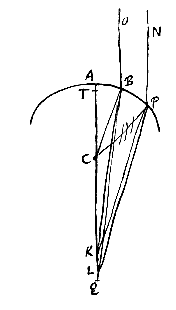
33 Voorstel 8: Gegeven een bol sferisch oppervlak van een doorschijnend lichaam, waarop van buiten evenwijdige stralen invallen. Te vinden het convergentiepunt van de gebroken stralen.
Hiernaast: onderste punt Q, met AQ / QC = n, als AC de kromtestraal is.
37 Voorstel 9: Idem, als evenwijdige stralen van binnen invallen.
39 Voorstel 10: Gegeven een hol sferisch oppervlak van een doorschijnend lichaam, waarop van buiten evenwijdige stralen invallen. Te vinden het divergentiepunt van de gebroken stralen.
41 Voorstel 11: Idem, als evenwijdige stralen van binnen invallen.
41 Definitie: Stralen corresponderen met een punt waarop ze gericht zijn, of vanwaar ze komen of schijnen te komen.
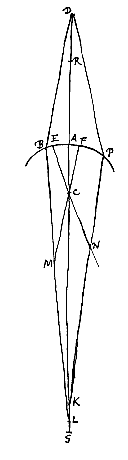 41 Voorstel 12: Gegeven een sferisch oppervlak van een doorschijnend lichaam, bol of hol, en een punt waarmee stralen corresponderen die naar dat oppervlak gaan. Het punt waarmee de gebroken stralen corresponderen is te vinden met een evenredigheid van afstanden op de as.
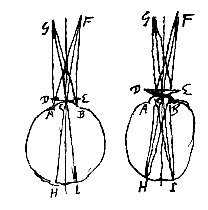
41 Voorstel 12: Gegeven een sferisch oppervlak van een doorschijnend lichaam, bol of hol, en een punt waarmee stralen corresponderen die naar dat oppervlak gaan. Het punt waarmee de gebroken stralen corresponderen is te vinden met een evenredigheid van afstanden op de as.
Hiernaast: oppervlak BAP, middelpunt C, bovenste punt D, onderste S, brandpunt R tussen D en A, evenredigheid DR : DA = DC : DS.
In onze notatie: (v – f1) : v = (v + r) : (v + b), met: v = DA, b = AS, f1 = AR, r = AC.
43 12.1: Bol oppervlak, stralen uit een punt, van buiten naar het oppervlak.
49 12.2: Idem, stralen naar een punt.
(Vondst van Huygens genoemd in van Schootens Commentaren op de Meetkunde van Descartes.)
67 12.3: Bol oppervlak, stralen uit een punt, van binnen naar het oppervlak.
71 12.4: Idem, stralen naar een punt.
73 12.5: Hol oppervlak, stralen uit een punt, van buiten naar het oppervlak.
75 12.6: Idem, stralen naar een punt.
77 12.7: Hol oppervlak, stralen uit een punt, van binnen naar het oppervlak.
77 12.8: Idem, stralen naar een punt.
Lenzen
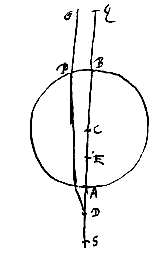 79 Voorstel 13: Gegeven een bol van doorschijnend materiaal. Te vinden het convergentiepunt van evenwijdige stralen.
79 Voorstel 13: Gegeven een bol van doorschijnend materiaal. Te vinden het convergentiepunt van evenwijdige stralen. 81 Voorstel 14: Idem, voor een platbolle lens.
83 Voorstel 15: Idem, voor een platholle lens, het divergentiepunt.
85 Voorstel 16: Idem, voor een willekeurige bolle lens, het convergentiepunt.
89 Voorstel 17: Idem, voor een willekeurige holle lens, het divergentiepunt.
(89: Eerste vermelding van het woord 'brandpuntsafstand' en daarmee van 'focus'.)
95 Voorstel 18: Een lens te vinden waarvan één bol oppervlak gegeven is, en die het convergentiepunt voor evenwijdige stralen op een gegeven afstand heeft.
97 Voorstel 19: Gegeven een lens met ongelijke bolle oppervlakken, of met de vorm van een maansikkel. Te vinden een andere gelijkwaardige lens die platbol of symmetrisch is.
99 Voorstel 20: Gegeven een bolle of holle lens, aan beide kanten sferisch of aan één kant plat. En op de as een punt, waarvandaan of waarheen stralen gericht zijn die naar de lens gaan. Het convergentie- of divergentiepunt na de tweevoudige breking is te vinden met een evenredigheid.