[ 361 ]

I  1). De menselijke stem. 1658. Dec. De verscheidenheid van tonen gebeurt door meer of minder vernauwing van het strottenhoofd. Klinkers.   a.  met open keel, maar het strottenhoofd wel tot een spleet samengetrokken, en door ontsnappende lucht. e.  ..... Enz. . . . . . . . . . . . . . . . . Dit stuk, meer van fysiologische dan van fysische aard, zal worden gepubliceerd bij de Varia [XXII, p. 195].   1)  Manuscript A, p. 65 [HUG 10, 33r]. II  2). Snaarlengten en trillingsgetallen.   § 1.  De oorsprong van het zingen komt van de samenklanken, ik bedoel zowel van het zingen van een enkele stem of instrument als van het meerstemmige gezang dat men tegenwoordig uitoefent. Want het genoegen dat men vindt in in het horen van samenklanken bestaat niet alleen met betrekking tot twee geluiden die tegelijkertijd samenklinken, maar is er evenzeer bij het horen van die tonen na elkaar. En zoals dissonantie onaangenaam is voor het gehoor als twee geluiden tegelijk worden gehoord, zo is ze het ook als deze zelfde geluiden achtereenvolgens worden voortgebracht, hoewel de grofheid niet helemaal zo groot is. . . . . . . . . . . . . . . . . . . . . . . . . . *)   2)  Portefeuille 27 (Musica), f. 56 e.v. Zonder datum.   [ *)  Weggelaten gedeelten in T. XX, p. 30.]

[ 362 ]

Nu moeten de eerste muzikale geluiden geweest zijn die welke het meest opvallend samenklinken, zoals het octaaf, de kwint en de kwart, als volgt: V F S V 2  1). En dit is inderdaad te zien aan het feit dat de eerste lieren slechts deze snaren hadden, en dat de gehele Oudheid slechts deze eerste samenklanken heeft erkend. . . . . . . . . . . . . . . . . . . . . . . . . . .   Aangezien de intervallen bij het zingen hun oorsprong hebben in de samenklanken, is het nodig ze voor al het andere te beschouwen, waarna we zullen zeggen hoe de genoemde intervallen eruit zijn voortgebracht. Het genoegen dat men had bij het horen van twee geluiden, hetzij van stemmen, snaren, herdersfluiten of iets anders, die samen een aangename vermenging maakten, gaf aanleiding te onderzoeken wat het verband was tussen zulke geluiden, waarin ze verschilden van andere die niet zo goed samengingen, en hoe men die samenklinkende geluiden volgens bepaalde regels kon vinden, steeds als men dat wilde.   Ik wil wel geloven dat het Pythagoras was die als eerste bedacht dit onderzoek te doen, want hij had een manier van denken, geneigd tot onderzoek van natuurlijke zaken en was heel talentvol; het is echter niet zo dat de hamers van de smid hem ertoe hebben aangezet 2), want stukken ijzer van de vorm die daartoe dient klinken geenszins helder. Het is mogelijk dat hij stukken aantrof van een of ander metaal met een betere vorm om te klinken dan hamers en dat hij opmerkte dat van gelijkvormige de grootste lager klonken. En hij kon met hun verschillende gewichten de verhouding bepalen van de samenklanken, omdat het waar is dat van twee gelijkvormige stukken metaal datgene dat tweemaal het gewicht heeft van het andere een octaaf lager klinkt; en als het anderhalf keer in gewicht is geeft het een kwint lager, en zo ook met de andere 3).   1)  Diatonische schaal: V R M F S L C V2 [Ut/Do, Re, Mi, Fa, Sol, La, Si, do].   2)  Het verhaal over de hamers is te vinden in h. 6 [... Gr.] van 'Harmonikon Encheiridion' van Nicomachus Gerasenus (in Musici scriptores graeci, ed. Carolus Janus, Lipsiae, Teubner, 1895). Nicomachus zegt uitdrukkelijk dat alle hamers van ijzer waren. Huygens las het ongetwijfeld in Antiquae Musicae Auctores septem [p. 10-11], gepubliceerd door M. Meibomius in 1652. Hetzelfde verhaal wordt verteld door Boëthius in De Institutione musica libri V [1867, p. 197], dat Huygens eveneens kende (portefeuille Musica); maar Boëtius heeft het niet over ijzeren hamers. Een vertaling van wat hij vertelt (boek I, h. 10-11) is te vinden op p. 840 van de Histoire des Sciences. Antiquité door Pierre Brunet en Aldo Mieli (Biblioth. scientif. Payot, Parijs 1935).   3)  We begrijpen niet hoe Huygens zo heeft kunnen spreken. Het gaat naar het lijkt niet om een eenvoudige vergissing. Na de zin die eindigt met "klinken geenszins helder" had hij namelijk eerst geschreven: "en de verhouding van hun gewichten ten opzichte van hun tonen zou niet geweest zijn zoals de schrijvers van dit verhaal zeggen [cursivering van ons]. Het is dus waarschijnlijker dat hij eerst de samenklanken heeft onderzocht door middel van gespannen snaren, verdeeld in bepaalde aantallen delen". Maar hij streepte deze zinnen door om er een blijkbaar onjuiste bewering voor in de plaats te zetten.   Het is inderdaad zeker dat niet het dubbele, maar het achtvoudige gewicht van een gelijkvormig voorwerp van hetzelfde metaal het octaaf geeft.   En dit was heel goed bekend. Mersenne zegt in zijn Harmonicorum libri (Harmonicorum instrumentorum libri IV, lib. 4 de campanis, Prop. VII) [Fr.] dat de lineaire afmetingen van een klok verdubbeld moeten worden "opdat ... een klok ... wordt verkregen die met de eerste een octaaf maakt". In "Harmoniae lib. IV (p. 364 van Cogitata physicomathematica, 1644) zegt hij uitdrukkelijk: "Behalve dit beviel mij in dat boek [manuscript van Joannes Faber] vooral dat hij op zeer veel waarnemingen vertrouwt, waaruit hij terecht concludeert dat 4 hamers in die verhouding die ze aan Pythagoras toeschrijven helemaal niet een verdeling van het octaaf in een kwart en een kwint maken, en dat het dus onwaar is dat hij de harmonische verhoudingen hieraan zou hebben ontleend".   Huygens vermeldt in een stuk van 1672 [T. XIII, laatste alinea van p. 804] "de regel van de smelters, die de middellijn van klokken verdubbelen waarvan ze willen dat de ene het octaaf van de andere heeft".

[ 363 ]

Enige oude schrijvers over muziek vertellen dat hij daarna volgens de gevonden verhoudingen gewichten vastmaakte aan koorden om ze te spannen, en dat hij vond dat tweemaal het gewicht het koord naar het octaaf erboven spande, en anderhalf maal naar de kwint, wat niet waar is. En als deze schrijvers zich de moeite hadden gegeven de proef te doen zouden ze hebben gevonden dat het gewicht van de eerste viermaal zo groot moet zijn om het koord een octaaf te laten stijgen, dat het als 9 staat tot 4 moet zijn om de kwint te maken, en dat in het algemeen de verhouding van de gewichten het kwadraat moet zijn van die welke de samenklanken bepaalt met de delen van een gespannen snaar 4). Als Pythagoras dus ook de samenklanken heeft onderzocht met door verschillende gewichten gespannen koorden, heeft hij het gevonden zoals ik zojuist heb gezegd, maar het is niet hieruit dat hij de verhoudingen van de samenklanken heeft vastgesteld, maar met de verdeling van de snaar of van de 'Canon', zoals ze dit vanouds noemden.   Het is nu niet nodig dat ik lang blijf stilstaan om alle samenklanken uit te leggen die met dit middel zijn te vinden en welke verhoudingen ze hebben, daar ze zo algemeen bekend zijn. Men weet dat het octaaf bestaat uit de dubbele verhouding, dat wil zeggen als er twee snaren zijn, in alles gelijk en met dezelfde spanning, waarvan de ene tweemaal zo lang is als de andere, heet de samenklank die ze maken een octaaf. Dat de kwint wordt gemaakt wanneer de ene zich tot de andere verhoudt als 3 tot 2, de kwart wanneer ze zijn als 4 tot 3, de grote terts wanneer ze zijn als 5 tot 4, de kleine terts wanneer de verhouding is van 6 tot 5, de grote sext wanneer deze is van 5 tot 3, de sext wanneer ze is van 8 tot 5.   Dit zijn alle samenklanken die men telt in de omvang van een octaaf, alle met een kleinere verhouding dan van 2 tot 1. Maar behalve deze samenklanken zijn er nog veel andere, die men replica's van de eerste noemt, en de oorsprong hiervan is: wanneer twee van zulke snaren zoals we hebben gezegd samen de een of andere van de   4)  In T. XVIII, p. 486 zijn de empirische wetten van Mersenne genoemd over trillingen van snaren. Prop. VIII van boek II van Harmonicorum libri is: "Om een gegeven snaar die een gegeven geluid maakt naar een hoger geluid te laten stijgen, moet hij worden gespannen door krachten, die tenminste een verhouding hebben van het kwadraat van het interval, dat moet worden bereikt". Galilei zegt in zijn Discorsi van 1638 eveneens (p. 100): "Dat als er [aan een snaar] eerst werd getrokken door een gewicht van een pond, het passend zal zijn er vier aan vast te binden voor verhoging naar het octaaf"  [Engl. 1730].

[ 364 ]

al genoemde samenklanken maken, dat men dan vindt dat elke snaar waarvan de lengte het dubbele is, of de helft — of anderszins een veelvoud van 2 of deelbaar door 2 ten opzichte van één van de samenklanken — ook consonant is met de andere of zelfs met het veelvoud of quotient met 2 van die andere. Zo is de verhouding van snaren die een grote terts maken die van 5 tot 4, en dan zal die van 10 tot 4 ook een samenklank maken, die de tiende heet, en die een van de replica's is van de grote terts, en met andere getallen is de verhouding ervan die van 5 tot 2.   En zo maken snaren van 3 tot 2 de kwint, en zal er ook een samenklank zijn van 6 tot 2 of van 3 tot 1, die men de twaalfde noemt, en het is een replica van de kwint. En de reden waarom dit voorkomt is dezelfde die de zoetheid van de andere samenklanken maakt.   § 2.  Wanneer men de trillingen van snaren onderzoekt, wat naar ik meen Galilei voor het eerst heeft gedaan 1), vindt men dat hun heen en weer gaan frequenter is naarmate ze korter zijn en dat het trillingsgetal precies in omgekeerde verhouding is met hun lengte. Ik wil het steeds hebben over snaren die gelijk zijn in alles en met dezelfde spanning, zoals wanneer men er gelijke gewichten aan hangt. Zo maakt die welke de helft in lengte is van een andere 2 trillingen in de tijd dat de andere er maar één maakt. Die welke tweederde is maakt 3 trillingen in de tijd dat de andere er 2 maakt, en evenzo met de andere samenklanken. En omdat dit maakt dat die welke hun lengte hebben als van getal tot getal samen tegen de lucht zullen slaan met geregelde tussenpozen, terwijl ze er onderling onsamenhangende slagen in zullen vermengen, maar op dezelfde manier bij elke herhaling; daarom is het dit geordend stoten tegen de lucht, dat bij de werking in ons oor het genoegen van de samenklanken voortbrengt. Het is echter niet zo dat het bewustzijn ook maar enigszins die slagen kan tellen of afzonderlijk waarnemen, of hun onderlinge meetbaarheid beschouwen, want er komt geen redenering aan te pas, maar het vindt ze aangenaam evenals de reuk de zoetheid van parfums ruikt, en de andere zintuigen behagen scheppen in andere objecten die ze kunnen beroeren. En ik denk dat het vergeefs zou zijn de oorzaak van deze genoegens verder weg te zoeken.   1)  Zie de volgende noot. Hoewel men er naar het schijnt vòòr Galilei niet in is geslaagd trillingsgetallen bij bepaalde tonen direct te meten, begreep men heel goed dat de toonhoogte afhangt van deze getallen. "Mersenne formuleert het eerste deel van de wet die zijn naam draagt precies — al in 1623 (Quaestiones celeberrimae in Genesim, col. 1559-1561) — als hij zegt dat de snaarlengte omgekeerd evenredig is met het trillingsgetal, en zo wijst hij het middel aan om bepaalde eigenschappen van snaartonen aan te brengen bij snaren van andere instrumenten. Laten we er echter op wijzen dat een streng bewijs van deze wet al in 1616 [1614] was ontdekt door Isaac Beeckman, die dit in 1618 had meegedeeld aan zijn vriend Descartes" (p. 136, noot 1 van T. I van de Correspondance du P. Marin Mersenne door Mme P. Tannery en C. de Waard). Dit bewijs — streng zo men wil — is verschenen in T. II van 1936 van deze Correspondentie (p. 234-236).

[ 365 ]

Wat ik heb gezegd, dat trillingsgetallen van snaren in dezelfde verhouding zijn, daarvan zou men kunnen denken dat het beweerd is zonder bewijs, aangezien de snelheid van een snaar die een of andere toon laat horen zo groot is dat het heen en weer gaan niet te tellen is. Maar in de eerste plaats is er de proef die Galilei gebruikte, die zegt dat hij heeft waargenomen, bij het schrapen van een mes over koper, dat terwijl dit schrapen een verscheidenheid aan tonen produceerde, het ook zichtbare tekenen naliet van de trillingen van het mes, die tweemaal zo dicht bij elkaar waren als het geluid een octaaf hoger was geweest. Waarbij is te veronderstellen dat de beweging van de hand bij dit schrapen steeds even snel was 2). Maar het bewijs kan men krijgen met de snaren zelf, door ze heel lang en weinig gespannen te nemen, en ook al geven ze geen geluid, het is voldoende om te zien dat de hele snaar zijn trillingen tweemaal zo langzaam maakt als de helft ervan, omdat men dan niet kan betwijfelen dat hetzelfde gebeurt bij klinkende snaren. In plaats van een heel lange snaar kan men ook korte nemen, maar langs de hele lengte gelijkmatig verzwaard op de manier waarop parelkettingen of gebedssnoeren zijn geregen; die moeten loodrecht gespannen worden met een gewicht aan het eind. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .   2)  Tegen het eind van de eerste dialoog van Discorsi e dimostrazioni [p. 101] van 1638 zegt de ene spreker dat "tellen van de trillingen van een snaar ... geheel onmogelijk is", wat een ander de gelegenheid geeft om de proef van het schrapen te vertellen, "de uitvinding is toevallig geweest" [Engl. 1730].

[ 366 ]

III. Theorie van harmonische trillingen en proeven met snaartrillingen.   Zie p. 489-494 van T. XVIII, datum 1673. IV  1). Proef om de "vermengde trillingen" van een snaar te zien.   Zoals men snaren van goud op kleine spinetten zet om bassen te hebben die laag gaan, of men niet hetzelfde zou kunnen doen door een beetje lood in het midden van de snaar vast te maken.   Ditzelfde gewicht vastmaken op tweederde om te zien hoe de snaar zal klinken.   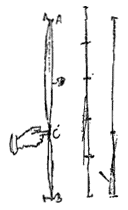Als men, na een snaar AB op het monochord te hebben gespannen, de vinger in C bij tweederde tegen de snaar brengt, en deze met de andere hand zacht laat klinken met het korte deel CB en meteen erna de vinger bij C weghaalt, zal de snaar alleen de 5e of liever de 12e laten horen van de toon bij de hele lengte AB.   Evenzo, als BC 2/5 of 3/5 of 4/5 van de hele snaar is zal men, door deze evenzo te laten klinken als tevoren, de 3e of de 10e horen. En het is waarschijnlijk dat deze trillingen ook nog gemaakt worden, hoewel zwak, als men de hele snaar over de gehele lengte laat klinken,   1)  Manuscript E, p. 54 [HUG 9, 29v], van 1675; de data 25 februari en 8 december 1675 staan resp. op p. 39 en 58.

[ 367 ]

en omdat er zoveel manieren zijn die deze 10e maken, is dit de reden waarom men hem altijd hoort bij het geluid van de over de gehele lengte klinkende snaar. En dat de 12e zich zo ook laat horen, maar zwakker omdat er maar twee verdelingen van de snaar zijn, zoals C en D, die deze 12e voortbrengen.   Om met het oog de vermengde trillingen van snaren te zien zou men een heel lange moeten verzwaren met eraan geregen bolletjes lood, met knopen ertussen, want de trillingen zouden heel langzaam worden ook al was de snaar strak gespannen.   Zonder op deze manier de trillingen te zien is het moeilijk te bevatten hoe het deel BC twemaal kan trillen terwijl het andere CA maar eenmaal trilt.

[ 368 ]

  [Fig. 118]  

Parallellepipedums van metaal op deze manier op schragen gezet [Fig. 118] geven een helderder geluid dan bij elke andere positie 2), en als er zandkorrels op worden gestrooid bij K en M en het parallellepipedum wordt aangeslagen zodat het klinkt, wordt duidelijk gezien dat het zand lichtjes opspringt en naar die plaatsen K en M wordt gebracht. Hiervan kan de reden worden gegeven.   De proef kan worden gedaan met een lange en dunne staaf, zo geschraagd dat de trillingen duidelijk zijn te onderscheiden en te tellen. Je zult zien dat er in M en K geen sprongen worden gemaakt.   P. S.  Ik heb onlangs gezien dat degenen die van dergelijke parallellepipedums cimbalen maken, de punten M en K (waar ze worden geschraagd) aan beide kanten op een afstand tot het uiteinde nemen van 2/9 van de gehele lengte. Uit deze berekening van ons is x groter dan 2/10 3). Dus het ligt er aardig dichtbij 4).   Een vraag: waarom moet bij de staven ED en AC, van gelijke dikte en materiaal, zodanig dat ED een octaaf hoger klinkt dan AC, de verhouding van ED tot AC zijn als van 1 tot √2, of als van de zijde van een vierkant tot de diagonaal? 5)   1)  Manuscript G [HUG 7], f. 12v en 13r, van 1688 of 1689: vergelijk p. 74 [75] hiervoor, met het begin van dit stuk, over een kwestie uit de statica.   2)  Zie echter noot 4 hierna.   3)  Zie de berekening van p. 75 hiervoor, waarbij x (CK in fig. 118) = a (√2 - 1) = 0,207 (2 a), waarin 2 a de lengte van de staaf is.   4)  Volgens p. 283 van Vol. 1 van The theory of sound van J.W. Strutt, baron Rayleigh (2e ed. 1894) liggen de trillingsknopen theoretisch op afstanden van 0,224 (2 a) van de uiteinden. 2/9 komt dichter bij 0,224 dan 2/10 of 0,207 (noot 3).   5)  Om de juistheid van deze experimentele uitkomst te bewijzen zou het nodig zijn geweest de trillingstheorie op te stellen van een staaf met gewicht (en uniforme doorsnede) die met het ene uiteinde vast zit in een muur, wat Galilei en Huygens niet konden doen: vergelijk noot 5 van p. 71 hiervoor.

[ 369 ]

Is het misschien zo dat de trilingen gelijke tijden hebben wanneer de lengte van staaf AB tot die van CD staat als gewicht D tot B, als het gewicht van de staven buiten beschouwing blijft en op nul gesteld wordt 6).   6)  Huygens kan hebben verondersteld, of met een proef gevonden, dat elke ingeklemde staaf altijd een zelfde toon geeft, zodat het gaat om harmonische trillingen. Nu is bij eenzelfde uitwijking de veerkracht, die het gewicht naar de evenwichtsstand drijft, waarschijnlijk n maal zo klein wanneer de gewichtloze staaf n maal zo lang is, en als de massa van het gewicht eveneens n maal zo klein is, dan is het redelijk te veronderstellen dat de trillingen van de twee staven dezelfde periode hebben.   [ Op p. 377 wordt een fluittoon vergeleken met "de toon van mijn koperen meetlat".]   [ Interessante informatie (inclusief het springende zand dat Huygens in het begin noemt) staat in: Quirinus van Blankenburg, Elementa musica (1739), p. 136-7:]   6.  Ik heb by den grooten Klokkegieter Hemony ... in 't jaar 1676 t'Amsterdam een Staafspel gezien waar van ieder staaf, op zyn kant gelegd zynde, een octaaf hooger klonk als op zyn plat: dit kwam van dat de dikte tegen de breedte stond als 1 tegen 2: zynde half zo dik als zy breed waren.   7.  Naar deze staven stelde hy zyn klokken; waar van wy hier zullen aantekenen, dat ... een klok zelden zo net gegoten word of hy zal aan d'een zy wel een weinig dunder zyn als aan d'andere: by gevolg dan vals. Om dit gebrek weg te nemen moet hy gedraait worden tot dat hy zuiver is, 't welk men aan de klank die hy in 't draayen geeft kan hooren. ...   8.  Het is een bekende zaak dat de glazen zullen antwoorden als men hen in hun taal aanspreekt ... zal ook een staaf terstond klinken als hy van een sterk geluid op zynen toon wordt aangetast. Hier door zyn zy 't model van de stelling der klokken ... zo haast als de klok op zyn toon is zal de staaf antwoorden.   9.  ... stukken yzer ... leggen op twee wolle koorden op zodanige tussenwydtens als zy zelver zullen aanwyzen: 't welk vermakelyk is om te zien; want als men een staaf daar een weinig droog zand op gestrooid is doet klinken, zo zal 't zelve, door die beweging, zig al springende op twee plaatsen verzamelen, daar 't dan zal blyven stil leggen, ten teken dat men aldaar mag een gat boren of een ander middel gebruiken om de staaf mee vast te maken, zonder aan 't geluid eenig hinder toe te brengen. [ Huygens kende van Blankenburg sinds 1681.] [>]

[ 370 ]

VI  1). Over geluid in het algemeen; tonen; voortplanting.   [Fig. 121]         § 1.  Dat geluid ontstaat door waarneming van de beweging van lucht door het oor.   Dat de toon komt van een regelmatige trilling van de lucht [Fig. 121] 2).   Dat deze trilling een bepaalde snelheid op zijn minst moet hebben.   Dat de sterkte van het geluid afhangt van de hoeveelheid lucht die bewogen wordt en dat daardoor een snaar die gespannen is op een klavecimbel of op een luit meer geluid geeft, dan gespannen op een muur, omdat de hele klankbodem van het klavecimbel of van de luit meetrillen met de snaar en alle lucht die is opgesloten en die er omheen zit.   Hoe deze klankbodems op verschillende manieren tegelijk kunnen trillen terwijl ze meer snaren samen laten klinken.   Dat er in het luchtledige geen geluid is 3).   Dat lucht veerkrachtig is en opeenvolgende bewegingen maakt door geluid 4).   Over geleiding van geluid door buizen en gewelven.   Over terugkaatsing van geluid.   Over de voortplantingssnelheid van geluid; deze snelheid vergelijken met die welke nodig is om het geluid te maken.   Over de donder.   1)  Manuscript E, p. 9-10 [HUG 9, 5r], van 1674. De datum 30 dec. 1673 staat in Man. D [HUG 2], p. 440 en Man. E, p. 26 heeft 19 dec. 1674.   2)  Vergelijk het eind van stuk VIII hierna [orgelpijp, p. 374]. [ In de tekening lijkt lucht geblazen te worden door een opening linksboven, tegen het 'labium' van een blokfluit of orgelpijp.]   3)  Zie p. 200, 208 en 239-240 hiervoor.   4)  Dit was al in de Oudheid onderkend. Volgens Alexander van Aphrodisias, De sensu, XXIII [Gr. 1901], leerde de filosoof Strato, opvolger van Theophrastus (zelf opvolger van Aristoteles) dat geluid ontstaat "door het bewegen [van de lucht] op gelijke wijze zich samentrekkend en uitstrekkend" Strato heeft het, om zo te zeggen, over longitudinale trillingen. [ De Griekse uitdrukking staat in 'Porphyriou eis ta armonika Ptolemaiou upomnèma', zie J. Wallis, Operum Mathematicorum volumen tertium (1699), p. 246 (Lat.: "quod moveatur similiter, contractus, & extensus"), Porphyrios Kommentar zur Harmonielehre des Ptolemaios, ed. I. Düring (Gr. en D.), 1932.]

[ 371 ]

Dat geluid wordt doorgegeven door water, hoewel zwak 5); dat water elastisch moet zijn.   § 2.  Over de verschillende manieren om muzikale geluiden voort te brengen.   Hoe snaren geluid geven, en fluiten, klokken, instrumenten met een tongetje, de keel, een buis met een gat dat is afgesloten door een verend plaatje.   Dat het octaaf wordt gemaakt met dubbel zoveel trillingen, de kwint door anderhalfmaal zoveel, enz.   Over de gelijkheid van de trillingen van een snaar.   Dat het viervoudig gewicht nodig is om hem met een octaaf te verhogen 6).   Dat een snaar na te zijn losgelaten weer omhoog komt.   Dat klokken in water een 10e lager klinken dan in lucht, pater Mersenne verzekert het 7). . . . . . . . . . . . . . . . . . . . . . . . . .   5)  Zie p. 240 hiervoor (proef van 20 dec. 1674). Huygens had misschien al wat eerder een dergelijke proef gedaan. Zie § 133, 134 van de 'Centuria secunda' van Sylva sylvarum of Historia naturalis van Bacon. Maar het was duidelijk al lang bekend: om te weten dat water geluid doorlaat waren geen laboratoriumproeven nodig. Zie h. VI van 'De sensu' van Aristoteles [Engl., ook: 'On the soul', part 8].   6)  Zie noot 4 van p. 363 hiervoor.   7)  Prop. XXX, p. 67 van 'Traitez de la nature des sons' (in Harmonie universelle van 1636): "hoeveel het geluid lager is in water dan in lucht". Mersenne zegt in het algemeen dat voor "het instrument dat in lucht en in water klinkt" het geluid "dat het heeft in water een grote tiende lager is", eraan toevoegend: "zoals alle proeven duidelijk aantonen, als men ze doet met een klok, enz.".

[ 372 ]

VII  1). Geluidssnelheid in lucht.   Voor de snelheid van het geluid.   § 1.  8 Okt. 1669.  Te Viry*).   Het huis dat de Echo maakte was van de plaats waar geschreeuwd werd verwijderd 1042 Rijnlandse voet wat 1005 Parijse voet is, zodat het geluid bij heen- en teruggaan een afstand aflegde van 2010 voet. En de tijd die het daarvoor gebruikte was 2 slingeringen van een slinger van 2 voet 7½ duim wat neerkomt op 1", 52"'. Dus daar het geluid in een tijd van 1", 52"' aflegt 2010 voet, zal het in 1" afleggen 1076 voet of ongeveer 180 toises 2).     § 2.  Om nauwkeurig te meten zou het nodig zijn dat het voorwerp dat het geluid maakt zelf de slinger zou loskoppelen, die maar een halve slingering zou maken en tegen een plank zou botsen, en de slinger zou beetje bij beetje verkort moeten worden totdat de Echo van de slag en de klop van de slinger tegen de plank op hetzelfde tijdstip in het oor kwamen.   § 3.  3000 bracci (een mijl) in 5 second. 3). Braccio van Florence.   1)  Het stuk (§§ 1-4) is ontleend aan f. 26v van de portefeuille 'Physica varia' [HUG 31].   [ *)  Logerend bij de broers Perrault. Er is een brief uit Viry aan broer Constantijn van 8 okt. 1669.]   2)  Met de nauwkeurige waarde voor de tijd (1 en 52/60 seconde) komt er 179,5 parijse toises.   3)  In 'Terza Esperienza' (p. 244) van de Saggi, Florence 1667 [Engl. p. 138]. De schrijvers noemen eerder de Stoïci [vergelijking met watergolven] en herinneren aan de ondervindingen van Gassendi, die zei dat de snelheid voor sterke en zwakke geluiden gelijk is. [P. Gassendi, Opera (1658) T. I, 418: kanon en musket.] [ Deze mijl van 3000 bracci was 5/3 km, volgens het regeltje: tussen bliksem en donder zit 3 s voor elke km.]

[ 373 ]

Een braccio is ongeveer 22 Rijnlandse duim.   600 bracci in een seconde zijn 183 toises in een seconde 4).   § 4.  Pater Mersenne geeft op pag. 44 van l'Utilitè de l'Harmonie 230 toises voor direct geluid in de tijd van een seconde en maar 162 toises aan het geluid van de Echo 5). Waaruit zou volgen dat het ongeveer 21 derden [zestigsten van een seconde] gebruikte bij het gaan en 39"' bij het terugkeren. Wat niet geloofwaardig lijkt.   § 5 6).  Maar het geluid gaat met 180 zesvoeten in 1" tijd.   180 Parijse toises = 351 m, terwijl 183 Rijnlandse vademen = 345 m.   Volgens de Historia van 1701 (p. 161) [1698, p. 158] van du Hamel vonden Cassini, Picard en Römer op 23 juni 1677 met behulp van een kanon 183 Parijse toises [1280 hexaped., 7 sec.], wat niet veel verschilt van de iets juistere waarde van Huygens. Maar die van de Florentijnen is nog beter. In het stuk IX dat volgt geeft Huygens te verstaan dat de snelheid zou kunnen veranderen met de temperatuur [aestate - in de zomer, en hyeme - in de winter].   4)  Het gaat hier om de Rijnlandse vadem [eveneens 6 voet]: met de braccio gelijk aan 22 Rijnlandse duim komt er 183 1/3 Rijnlandse vadem (of 177 Parijse toises).   5)  Harmonie universelle, 1636 [Seconde partie, 1637]. Mersenne (evenals Gassendi die geluidsatomen aanneemt) denkt niet aan een trillende beweging van lucht: naar aanleiding van de echo (p. 50 van de verhandeling 'De la nature des sons') vraagt hij zich af "of het dezelfde lucht is die terugkomt". [Vgl. Beeckman, 'idem numero': luchtdeeltjes uit de mond van de spreker gaan de oren van de toehoorder in.]   In de Cogitata physicomathematica van 1644 geeft Mersenne voor de snelheid van direct geluid dezelfde veel te grote waarde van 230 Parijse toises [per seconde], die hij zegt uit proeven te hebben gevonden — zowel in de 'Ballistica' (Prop. XXXV [XXXIX, p. 138]) als in 'Harmonicae lib. I' (Prop. V [p. 274]).   6)  Manuscript I, f. 123 r [HUG 8, 61r], van eind 1694 of begin 1695. De waarde 180 toises is die van 1669 (§ 1).   [ Wikipédia: in 1738 werd met kanonschoten de snelheid van het geluid gemeten over een afstand van 28,5 km (de tijd was 1' 25"); zie Nollet, Natuurkundige lessen, 3-2 (1761), p. 358 — Leçons de physique expérimentale, 3 (1745), p. 421;  Mém. de l'Ac. des Sc. 1738, p. 128;  Phil. Trans. jan. 1708: William Derham, 'Experimenta & observationes de soni motu'. De proef is ook gedaan in 1822, zie Handboek der natuurkunde, 1871, p. 201 (met afbeelding). Simon Stevin had al pogingen gedaan om de geluidssnelheid te bepalen m.b.v. kanongebulder, zie Is. Beeckman, Journal II, 427.]

[ 374 ]

VIII  1). Opeenvolgende echo's van traptreden. Tonen van orgelpijpen.   24 Nov. [1680].  Te Chantilly geweest .... Cascade van de rivier, 9 voet hoog, 15 voet breed, aan het eind van het kanaal op de zeshoek. Echo van de waterfontein beneden tegen de treden van de grote trap van het terras, maakt een toon als van een trompet in de verte, wat komt van de opeenvolgende echo's van de traptreden die 17 duim breed zijn. Het lijkt me dat er 45 treden zijn of zo .... 3 Dec.  Teruggegaan naar Chantilly, de trap was vol sneeuw die de treden bedekte tot de helft van hun hoogte. Het geluid was er helemaal niet meer te horen.   Een buis van 17 duim maakt als je erin blaast dezelfde toon als de echo van de trap, wat mijn opvatting bewijst, omdat die 17 duim de breedte van de treden is. ........   Hetzelfde in een stuk van 1693 in Manuscript I [HUG 8, 43r-v] (brief aan de la Hire?) dat gepubliceerd is op p. 570-571*) van T. X. Om te rechtvaardigen wat hij zegt over de buis van 17 duim voegt Huygens eraan toe: dat de lengte van een orgelpijp de toon bepaalt, die hij door zijn lengte heeft, omdat de stootjes van de lucht eveneens aankomen met de kleine tijdsintervallen die zijn golvingen gebruiken om tweemaal de lengte van de pijp af te leggen, te weten wanneer hij aan het eind gesloten is 2).   Kennis van de 'golflengte' in het geval van buizen stelde Huygens in staat de trillingsfrequentie van een gegeven toon te berekenen, aangenomen dat de geluidssnelheid bekend is. Vergelijk het eind van stuk IX.   1)  Het stuk is ontleend aan p. 251 van Manuscript E [HUG 9, 125r].   [ Christiaan was eerder in Chantilly geweest met broer Lodewijk, zie diens dagboek bij 29 juli 1655.  Een foto van de grote trap ('le Grand Degré') is hier te zien (2 keer te vergroten), het aantal treden lijkt te kloppen.]   [ *)  Zie M. Minnaert, De natuurkunde van 't vrije veld, deel II (1939), § 30: vertaling, en waarneming te Chantilly zonder ruisende fontein. En: Frans A. Bilsen, 'Huygens on pitch perception', in Journaal van het NAG, 178 (2006) 1-8.]   2)  Vergelijk Prop. XI ('De verschillen van open en gesloten en alle andere pijpen te vinden') van boek III ('Over orgels ...') van Harmonicorum instrumentorum libri van Mersenne. Maar we zien niet dat Mersenne zoals Huygens (zie het stuk IX dat volgt) de relatie begreep tussen de snelheid van het geluid, het aantal trillingen per tijdseenheid van een toon, en de golflengte ervan. Hij zegt over open en gesloten pijpen alleen: "Als [de pijp] wordt afgesloten klinkt hij een octaaf lager, omdat er hetzelfde gebeurt als wanneer hij tweemaal zo lang was, aangezien de lucht de weg tweemaal aflegt [vgl. p. 373, noot 5, eind 1e alinea], of tweemaal zo langzaam beweegt". [ Fr. p. 319; "de wind die men in de gesloten pijpen stuwt doet de weg tweemaal"; zie ook p. 359: "twee keer zoveel weg ... kaatst terug tegen de volgende wind, waarvan hij de snelheid tegenwerkt", en p. 396: moeilijk te verklaren.]

[ 375 ]

IX  1). Experimentele bepaling van de trillingsfrequentie bij een toon. De golflengte.   Wanneer het rad AB eenmaal wordt omgedraaid en bovendien een deel van de omtrek dat gelijk is aan 3 3/10 duim, wordt het rad CD twaalf maal omgedraaid. En dit eenmaal, dan roteert het asje FE 53 maal.   Van een slinger met lengte een voet min 1/60 voet kwam de slingering heen en weer steeds overeen met één omwenteling van rad AB.   En toen gaf het asje FE een geluid als de D of Re van mijn klavecimbel, die een toon hoger is dan de toon van een grote klok in de zogeheten St. Jacobskerk 2) op onze Haagse markt, waarvan de toon namelijk samenklinkt met de C van het klavecimbel of de Ut.   De middellijn van rad AB is 1 voet en 11 8/10 duim, of AB is 2 voet min 2/120 of 1/60.   Dus 3) wanneer rad AB eenmaal omdraait, worden er 11 1/2 omwentelingen van rad CD gemaakt, en 609 omwentelingen van asje FE. Dientengevolge zullen er elke seconde 547 omwentelingen van asje FE gemaakt worden.   1)  Het stuk is ontleend aan een apart blad (portefeuille 'Musica') [HUG 27, 23r] dat ook opmerkingen heeft over Wallis' vertaling van de Harmonika van Ptolemaeus (genoemd op p. 355, n. 7). Het is zeer waarschijnlijk van na 1682. Het gaat zoals men ziet om een proef die 's winters gedaan is in den Haag.   2)  De Grote of Sint-Jacobskerk die nog steeds bestaat [en waarvan een klok te horen is bij Wikipedia].   3)  De berekeningen zijn weggelaten. [ Vgl. XX, p. 105: een tekening die een sirene kan voorstellen, een ander apparaat waarmee geluidsfrequenties te bepalen zijn — maar dit is nogal onzeker, zie XXII, p. 199-.]

[ 376 ]

180 vadem (1080 voet) — ik neem aan Rijnlandse — gaat het geluid in 1". 's Zomers in Frankrijk 4). 1080 547 bijna 2 voet   D.w.z. als het asje bij elke omwenteling een trilling maakte, zond het een toon uit met een golflengte van bijna 2 voet. Weliswaar gebruikt Huygens de uitdrukking 'golflengte' niet, maar hij heeft er blijkbaar een heel helder idee van, wat niet het geval is bij Mersenne: zie p. 374, noot 2.   Een pijp van een voet echter, en dus ook van twee voet 5), Rijnlands, klinkt nauwelijks zo hoog als de Ut van het klavecimbel, 's winters in Holland.   Er zit misschien een zekere fout in hetzij de meting van de geluidssnelheid, hetzij de omtrekken van de raderen en van het asje EF. Waarbij misschien ook de draad wat slipte, en de beweging van het asje niet geheel volgde, zodat er anders meer dan 547 omwentelingen waren geweest, waardoor ook de uitkomst van de deling iets minder was geweest dan 2 voet 6).   4)  Huygens had kennelijk niet zijn notities bij de hand over de proef van 1669 (stuk VII). Hij vergist zich waar hij zegt een snelheid van 180 rijnlandse vadem te hebben gevonden. De hier aangenomen waarde is evenwel juister: 339 m/s.   5)  De beschouwde pijpen waren blijkbaar open; de kleine gaf zijn grondtoon, de grote het octaaf van zijn grondtoon. [ Een open pijp is ongeveer half zo lang als de golflengte van zijn grondtoon (een gedekte pijp een kwart).  1 Rijnlandse voet = 0,314 m. Een wijdere pijp geeft een lagere toon: volgens Mersenne (^) daalt de toon van een halfvoetspijp een kleine terts bij verdubbeling van de diameter. De frequentie volgt uit een formule van A. Cavaillé-Coll, in Comptes rendus, 1860, p. 179 (met 'vibration' wordt bedoeld halve trillingstijd):  pijplengte = v/2f - 5d/3. Een pijplengte van 0,314 m en een diameter van 3 cm geeft bij 0 °C (v = 332 m/s):  f = 456 Hz. Met d = 6 cm komt er f = 401 Hz (meer dan een hele toon lager). Met d = 3 cm bij 20 °C (v = 343 m/s):  f = 471 Hz (minder dan een halve toon hoger). De temperatuur is dus van minder belang dan de diameter.]   6)  Het getal 547 is berekend met de aanname dat het asje FE 53 keer ronddraait als het rad CD één keer ronddraait. Maar het lijkt Huygens mogelijk dat bij deze proef de draad het asje niet precies meesleepte, terwijl bij de snellere beweging van het apparaat (waarbij het asje een toon geeft) het meeslepen vollediger is, zodat het getal 53 om deze reden vervangen zou moeten worden door een wat groter getal. Het getal 547 is inderdaad waarschijnlijk lager dan het ware getal, aangezien volgens een moderne tabel de noot C of Ut4 517 trillingen per seconde heeft en de erbij horende noot D of Re 581. [ Deze C van 517 Hz hoort bij een A van 435 Hz; nu is de standaard-A 440 Hz en de C 523 Hz.  Zie ook 'History of pitch standards' en een tabel uit 1880 bij 'Dolmetsch online'; hier ook 'Physics of musical instruments'.] [ De Sint-Jacobskerk laat nu een Bes horen, f = 466 Hz.  Maar dit zal niet de C van Huygens' klavecimbel zijn geweest, want dan was zijn D 524 Hz, bijna een halve toon lager dan de gemeten 547 Hz.]

[ 377 ]

[Fig. 124.]   Of de toon van een fluit [Fig. 124] verandert wanneer de lucht meer of minder samengeperst is, zodat de toon lager is in minder samengeperste lucht. Nee.   Met deze vier gaten [b] dicht is mijn fluit op de toon van mijn koperen meetlat, als de barometer op 16 graden staat. [Fig. 125.]     Of bij blazen in het mondstuk van een holte, gemaakt van twee cilinders van ongelijke dikte [Fig. 125], de toon dezelfde is als in een cilinder die overal even dun zou zijn als die waarin geblazen wordt, en met dezelfde inhoud als die twee ongelijke (ik neem aan dat er alleen een opening is bij het mondstuk). Ja. [Fig. 126.]   Welke toon een pijp maakt die zich opent in de vorm van een kegel [Fig. 126].   1)  Physica varia, f. 11 r. [HUG 31, afbeelding in Yoder 2013]. De datum 1675 staat op de achterkant. [ Dat geluid niet door het luchtledige gaat had Huygens proefondervindelijk bewezen in 1674.] [ In 1686 maakte hij een tabel voor de tonen van zijn fluit, zie XX, p. 104.]