Muziek

Ik luister niet naar wie zich beroept op autoriteit ¹).

  Muziek makend vanaf zijn kinderjaren ¹²), geeft Huygens in verscheidene van zijn brieven, b.v. in die geschreven te Parijs tijdens zijn verblijf van 1655 ¹³), blijk van zijn belangstelling voor deze kunst. Vanaf 1661, datum van de 'Divisio Monochordi' (p. 49 hierna), een maand nadat hij een geschrift van Hemony onder ogen had gehad, zien we hem zich aktief bezig houden met de theorie ¹⁴).
Overigens kunnen enkele van zijn theoretische notities niet van voor 1691 zijn; in dit jaar verscheen het boek van Werckmeister dat hij bespreekt ¹⁵). Het is ook in 1691 dat gedrukt werd zijn studie over de Harmonische Cyclus ¹⁶), veel eerder ondernomen. We herinneren eraan dat deze algemeen bekend staat onder de naam

  Voor andere bijzonderheden, deels chronologische, wordt de lezer verwezen naar de Voorberichten van de verschillende stukken die grotendeels zijn ontleend aan de portefeuille 'Musica' en die eindelijk de figuur van Huygens als musicoloog met enige precisie doen kennen, 250 jaar na zijn dood.

  Opgemerkt dient te worden dat Huygens in dit Stuk er blijk van geeft het bestaan van de harmonische boventonen te kennen — al beschreven door Mersenne ¹) — en dat hij zelfs een zeker verband legt tussen dit verschijnsel en dat van consonantie. Inderdaad, aangezien de boventonen die met de grondtoon een interval vormen van een of meer octaven, maken precies de 'replieken' die voldoen aan het criterium van de boven­bedoelde herleidbaar­heid van de karakteristieke verhoudingen, ze dragen bij tot het voortbrengen van consonantie.

  Huygens gelooft te kunnen conatateren — hier, zoals in verscheidene andere Stukken — dat de Ouden ("een vrij vreemde zaak") in het algemeen ²) slechts als consonant interval hebben erkend het octaaf, de kwint en de kwart, evenals die welke eruit voortkomen door toevoeging van een octaaf; maar niet de tertsen en sexten ("die", voegt hij eraan toe, "hoewel miskend toch gebruikt werden in hun zang van opeenvolgende tonen, evenals in die van tegenwoordig").
Mersenne zei ongeveer hetzelfde in het 'Livre Premier des Consonances', dat deel uitmaakt van Harmonie Universelle; hij schrijft (Prop. 29): "Het schijnt dat de Grieken geenszins deze 2 Tertsen, noch de Sexten, tot de Consonanten hebben gerekend, want allen vanaf Aristoxenos tot aan Ptolemaeus, Aristides, Bryennius*), en verscheidene andere zowel Griekse als Latijnse schrijvers, hebben slechts

Deeltonen van een snaar (Wikipedia)

  Blijkbaar was de tegenstelling tussen de gezichtspunten van de oude Grieken aan de ene kant, en die van onze zestiende en onze zeventiende eeuw aan de andere kant, niet zo scherp als het lijkt in de uitspraken van Huygens. Het is zeker, wat hij ook zegt, dat men het in de oudheid niet absoluut eens was op dit punt: Ptolemaeus verwijt de pythagoreëers de grote terts niet tot de rij intervallen (octaaf enz.) te hebben gerekend, waarvan sprake was in het begin van de vorige alinea.

  Het is naar ons inzicht niet voldoende. om het Griekse denken te karakteriseren,alleen de begrippen consonantie en dissonantie te beschouwen. Ptolemaeus maakt in elk geval een fijner onderscheid ³): hij stelt in de eerste plaats de emmele [harmoniërende] intervallen, d.w.z. die waarvan de twee tonen, achtereenvolgens gehoord, aangenaam zijn voor het gehoor, tegenover de ekmele [niet harmoniërende] die deze eigenschap niet hebben; in de tweede plaats de symfone intervallen, d.w.z. die waarvan de twee tonen schijnen samen te smelten, tegenover de diafone waarbij ze voor het gehoor hun eigenheid bewaren. Van deze vier soorten lijken alleen de niet harmoniërende de naam dissonant te verdienen; dus bij Ptolemaeus maken de tertsen, evenals de grote toon en de kleine toon, er geen deel van uit.

  In een brief aan Mersenne van maart 1622 ⁴) schreef J. Titelouze:

degenen die pythagoreïsche musici waren, hadden en gebruikten slechts de consonanties bevat in het 4 [tetrachord], en de leerlingen van Ptolemaeus bedienden zich van alle die zich konden bevinden in het 6 [hexachord].   Zie over de senarius p. 162 hierna [n.27 en n.30].

  In § 3 van Stuk A neemt Huygens stelling tegen Stevin, die in zijn Hypomnemata mathematica van 1608 (om alleen de Latijnse editie van dit jaar te noemen) het had gedurfd te beweren dat de Grieken zich vergist hadden door de verhouding 3 : 2 te beschouwen als een precieze uitdrukking van de kwint die aangenaam is voor het oor*); wat te verklaren is met het feit dat Stevin beweerde dat alle twaalf halve tonen van de toonladder gekarakteriseerd werden door een enkele verhouding. Het is bekend dat in de praktijk deze 'gelijkzwevende stemming' het op den duur heeft gewonnen bij de bouw van instrumenten; wat niet wil zeggen dat Stevin theoretisch gelijk had. We komen in noot 9 van p. 32 — waar o.a. sprake is van een manuscript van Stevin — terug op deze kwestie, die al is aangeroerd in

  Overigens wordt de invloed van het genoemde manuscript onthuld, denken we, op een al gepubliceerde plaats van het nu gepresenteerde Stuk 1, A (dat een geheel vormt met Stuk II over het geluid, gepubliceerd in 1937 in T. 19, p. 361-365); dit — of liever wat Huygens verkeerd zegt, of deze fout nu te wijten is aan de invloed van Stevin of niet — maakt het ons mogelijk de datum van het Stuk met een zekere waarschijnlijkheid vast te stellen. De laatste alinea van noot 3 van p. 362 van T. 19 liet al zien dat het waarschijnlijk van voor het jaar 1672 is; daarin heeft Huygens het over een "regel van de smelters" ^#), in strijd met wat Huygens dacht te kunnen uitspreken in het Stuk, als hij het heeft over het verhaal van de hamers van Pythagoras.
We hebben in de genoemde noot gezegd niet te begrijpen hoe Huygens in het Stuk, ondanks Mersenne ⁵), met de schrijver vasthoudt aan dit verhaal, "dat het waar is dat van twee gelijkvormige stukken metaal datgene dat het dubbele gewicht heeft van het andere een octaaf lager klinkt". Nu geloven we het te begrijpen: het is omdat Stevin in zijn geschrift dat Huygens kende het verhaal van de hamers vertelt zonder het te bekritiseren ⁶); hij zegt, wat lijkt aan te tonen dat hij inderdaad gelooft aan de werkelijkheid ervan, of althans de mogelijkheid: "Dergelijcke voorder besoeckende op speeltuygens gespannen snaren bevant daerin het selve regel te houden", d.w.z. "Dergelijke effecten vervolgens [d.w.z. na de hamers te hebben gewogen] onderzoekend op gespannen snaren van muziek­instrumenten, bevond hij [Pythagoras] dat daarbij dezelfde regel geldt". Wie zijn nu die 'smelters' die Huygens de ogen hebben geopend? Zonder twijfel de gebroeders Hemony, of liever een van beiden, met wie Huygens een lang gesprek had

  Tot slot halen we uitdrukkelijk op wat al is aangeduid in het begin van dit Voorbericht [p. 25], te weten de propositie van Huygens ⁸), voortaan de verhoudingen die overeenkomen met de verschillende intervallen niet te beschouwen als verhoudingen van lengten van snaren (van dezelfde aard en gelijk gespannen), maar als verhoudingen van trilings­frequenties, daar in de zeventiende eeuw was vastgesteld dat deze verhoudingen onderling omgekeerd evenredig zijn ⁹).
Overigens is het mogelijk dat dit verband al veel eerder is vermoed: als men de werken van de Griekse theoretici leest, wordt men er dikwijls toe gebracht zich af te vragen of het in hun gedachten het kleinste getal van de verhouding is dat overeenkomt met de hoogste toon, of veeleer (ondanks de beschouwing van de snaarlengten) het grootste van de twee getallen.

  Wat dus heeft gemaakt dat de mensen overal op aarde met dezelfde intervallen zingen, dat is geen toeval, noch een zeer vreemde zaak, maar al die intervallen zijn bepaald door de consonanten, en daar de muziek genoegen moest geven en geen verdriet, kon ze niet gezongen worden met andere intervallen dan deze.

  § 2.  Wanneer men zingt V R M F S L C V², ²) zijn er de tonen V M F S L V² die alle een consonant maken met de eerste V. En verscheidene ook onderling. En dat maakt ten eerste dat het voor het oor aangenaam is na elkaar te horen die, welke een consonant maken met de onmiddellijk voorafgaande, zoals V M S V² F L V² S V. Ten tweede houdt het er ook van, ze na elkaar te horen, hoewel ze niet consonant zijn met de onmiddellijk voorafgaande, maar met de voorlaatste of zelfs andere vorige, vooral wanneer ze enige indruk hebben gemaakt.
Zo geeft bij het zingen van V S F M F S L S S V de derde toon F een goed effect omdat deze consonant is met de eerste V. En de 4e toon M tegen de voorgaande S en V; en de volgende F tegen de voorgaande F (want hier is eenstemmigheid in plaats van consonantie) en tegen de V. De tweede S tegen de voorgaande MSV. En de L tegen FMV.

  Nu moeten de eerste muzikale geluiden geweest zijn die, welke samen

²)  Vergelijk noot 1 van p. 362 van T. 19. De tekens van de diatonische ladder V, R, M, F, S, L, C, V² komen dus respectievelijk overeen met C, D, E, F, G, A, B, c, of met DO, RE, MI, FA, SOL, LA, SI, do. [De door Huygens genoemde C is dus onze B.]  Bijgevolg is C = Bes.

  En ziedaar alle tonen van het octaaf waarmee de stem bij het zingen stijgt. Dat deze tonen deze oorsprong hebben, is er deels de oorzaak van geweest dat de ouden niet hebben overwogen dat de grote en kleine terts ens de sexten consonanten waren. Hoewel miskend zijn ze toch gebruikt in hun gezang van opeenvolgende tonen, evenals in dat van tegenwoordig. Het is waar dat het een nogal vreemde zaak is, dat ze niet vonden dat akkoorden met een afstand van deze intervallen van tertsen en sexten een aangenaam geluid maakten evenals de kwinten en de kwarten, en dat terwijl men nu geen akkoord maakt waar geen terts of sext in komt, men in hun tijd niet vond dat ze de naam consonant zouden verdienen. Maar we zullen later over de oorzaak hiervan spreken ⁴).
Wat betreft de oorsprong van de halve tonen, dat wil zeggen de andere tonen die wij soms zingen en die verschillend zijn van de voorgaande, het was noodzakelijk dat de C ⁵) als eerste werd gevonden, doordat men vond dat het stijgen van F tot aan C een slecht effect gaf wanneer de indruk van F in het oor bleef, die helemaal niet consonant is met C, en alleen met de S ⁶), die er zelf niet aan vooraf gegaan kon zijn.

  Maar stijgen via FSLC was nog veel aangenamer, omdat de C consonant is met S en met F,waarmee hij de kwart maakt; die een van hun eerst bekende intervallen was, wat maakt dat makkelijk dat geluid van de C werd gevonden. De andere geluiden die men chromatisch noemt kunnen gevonden zijn met cadensen op de plaatsen waar men een hele toon moest dalen, zoals S^\F^/S, LSL en RVR ^{6 bis}), want de stem is van nature geneigd zich niet zover van een toon te verwijderen waarop ze meteen terug moet komen, zodat men deze tonen vermindert. Maar dat er juist grote halve tonen van gemaakt zijn, daar zijn twee redenen voor, de ene dat de geluiden F^*, S^*, V^* 7) die zijn welke consonant zijn

  Vervolgens heeft men nog toegevoegd de M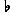, niet zozeer om de grote halve toon te hebben boven de R, als wel om de kleine terts boven de V te hebben en de grote onder de S, wat tegelijk de grote sext geeft tegen V² en de kleine sext tegen S omlaag.

  Men voegt er soms nog andere tonen aan toe en niet zonder reden, waarover we hierna zullen spreken ⁸).

  § 3.  Aangezien de intervallen bij het zingen hun oorsprong hebben van consonanten, is het nodig ...
. . . . . . . . . . . . . . . . . . . . . . . . .
  Zie p. 362-364 van T. 19 (Huygens heeft het er o.a. over het verhaal van de hamers van Pythagoras; zie hierover het Voorbericht [p. 28]), tot aan de alinea die eindigt met "de verhouding ervan met andere getallen is die van 5 tot 2" [T. 19, p. 364]. Op dee bladzijden is sprake van de 'replieken' waarop Huygens doelt aan het eind van de voorgaande paragraaf [p. 30]; zie de volgende alinea.

  En zo maken snaren van 3 tot 2 de kwint, en zal er ook consonantie zijn van 6 tot 2 of van 3 tot 1, die men de twaalfde noemt, en het is een 'repliek' van de kwint. En de reden waarom dit voorkomt is dezelfde die de zoetheid van de andere consonanten maakt, waarover we het zullen hebben.

  Het staat vast door ondervinding, en degenen die maar een beetje oor hebben voor muziek kunnen het niet ontkennen, dat de consonanten volgens de bovengenoemde verhoudingen heel volmaakt zijn en beter dan wanneer men zich verwijdert van deze werkelijke getal­verhoudingen. En degenen die het gewaagd hebben het tegendeel te beweren en dat de kwint niet bestond in de verhouding van 3 tot 2, of die niet een gehoor hadden dat in staat was erover te oordelen, of geloofden een reden ervoor te hebben, die concludeerden verkeerd  [In de marge:]  Stevin. ⁹).
waarover we hierna zullen spreken ¹⁰).

  We merken op dat het door Bierens de Haan gepubliceerde manuscript van Stevins verhandeling deel uitmaakt van een verzameling manuscripten — Vol. 47 genoemd in noot 1 van p. 516 van T. 18 — herkomstig van Constantijn Huygens sr. In een brief aan Mersenne van 1 april 1640 (ed. Worp, T. 3) spreekt deze laatste over "stukken van zijn hand [van Stevin] die nog niet het licht hebben gezien en die in mijn bezit zijn", Christiaan Huygens heeft dus heel goed kennis kunnen nemen van dit geschrift hoewel het geen plaats heeft gekregen in de Wisconstige Ghedachtenissen van Stevin, noch in de Latijnse vertaling van hetzelfde jaar 1608, Hypomnemata Mathematica, waarvoor het bestemd was (genoemd in het overzicht). [Vyfde Stuck, ook op p. 107.]

  Deze hypothese, hoe plausibel ook — we hebben het al laten uitkomen in ons Voorbericht, sprekend over de kwestie van de hamers van Pythagoras [p. 28] — is hier overigens min of meer overbodig, aangezien Stevin zijn systeem al kort had aangegeven in zijn 'Eertclootschrift', dat deel uitmaakt van zowel de Wisconstige Ghedachtenissen [p. 21] als van de Hypomnemata (I Liber Geographiae, p. 19). Deze passage is ook te vinden in de Oeuvres Mathematiques de Simon Stevin augmentées par Albert Girard van 1634 (p. 112 in 'Premier Livre de la Géographie'). Stevin spreekt er van de

groote gemeene oude raserie inde stof der Singconst {Matheriæ Musicae.} vande redens der toonen, waer in de palen der vijfde gestelt sijn van 3 tot 2 ... ... ware halftoonen die wy uyter natuer al evegroot singen ...

Van toen af aan waren deze mening van Stevin en het systeem dat hij eruit afleidde algemeen bekend. Mersenne noemt ze in zijn 'Preface, & Advertissement au Lecteur' van de 'Traitez des Consonances, des Dissonances, des Genres, des Modes & de la Composition', in Harmonie Universelle van 1636; Hij zegt:

Iedereen is vrij een mening te volgen zoals die wil, om de waarschijnlijkste redenen, bij voorbeeld: degenen die liever eraan willen vasthouden dat alle tonen en halve tonen gelijk moeten zijn ... zoals Stevin doet aan het begin van het eerste boek van zijn Geografie, en de Aristoxenianen van Italië met verscheidene anderen*), en niet ongelijk, zoals Ptolemaeus ze stelt, het zal ze niet aan redenen ontbreken; en het zal moeilijk zijn hun te bewijzen dat de Kwint juist in de verhouding van anderhalf is, en de toon in de verhouding van negen-achtste, ofwel dat er een duizendste aan ontbreekt, enz.   *)  Elders brengt Mersenne meer uitdrukkelijk de gedachte van Aristoxenos en de Aristoxenianen naar voren: zie de laatste alinea van deze noot; zie bovendien over het systeem van Aristoxenes noot 5 van p. 78 hierna, evenals noot 16 van p. 113 en noot 69 van p. 121 — waar sprake is van Vincenzo Galilei.

  Ook in 1634, dus iets eerder, in Les Questions theologiques, physiques, morales et mathematiques, sprak Mersenne in zijn antwoord op 'Question XXXIII. A quoy servent les raisons, & les proportions de la Geometrie, etc.' over: "degenen die gelijkheid van tonen volgen, en van halve tonen in de Muziek", die "gedwongen zijn 11 middel­evenredige lijnen te vinden tussen de 2 die het octaaf maken". [Zie Voorbericht, p. 28.]

  Ook Descartes wist van dit systeem. In zijn brieven aan Mersenne van 1634 heeft hij het drie keer over "uw musici, die de verhoudingen van consonanten ontkennen", "die ontkennen dat er verschil is tussen de halve tonen" (Oeuvres de Descartes, ed. Adam et Tannery, T. I, p. 286, 288, 295) en in een brief van 1 november 1635 aan Constantijn Huygens [p. 331] spreekt hij over

toch goede musici die nog niet willen geloven dat de consonanten verklaard moeten worden met rationale getallen, wat als ik me goed herinner de fout van Stevin was, die niettemin bekwaam was in iets anders.

  Het is misschien Isaac Beeckman die de aandacht van Descartes heeft getrokken naar dit onderwerp, hem bekend sinds 1614. In een brief aan Mersenne van 1 oktober 1629 schrijft Beeckman:

Daarom heb ik die mening van onze Stevin over zes tonen in voortdurende evenredigheid, vroeger door mij zeer nauwgezet aangehangen, al vele jaren geleden geheel en al verworpen.

Beeckman had trouwens in 1624 de gelegenheid gehad het hierboven genoemde manuscript van Stevin te raadplegen. We ontlenen deze informatie aan p. 274 en 286 van T. 2 van 1936 van de Correspondance du P. Marin Mersenne, gepubliceerd door Mme Paul Tannery, uitgegeven en geannoteerd door Cornelis de Waard.

  Anders dan Huygens die misschien een fijner gehoor had, keurde Mersenne het systeem van de Aristoxenianen en van Stevin in de praktijk niet af. Hij schrijft (Harmonie Universelle, p. 132, Livre Second. Des Dissonances, Prop 11: 'Expliquer les intervalles Harmoniques consonans & dissonans qui ne peuvent s'exprimer par nombres'):

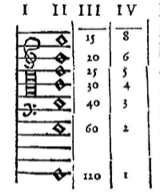
deze verdeling van het octaaf*) kan voldoen voor allerlei soorten Muziek, met Stemmen zowel als Instrumenten; want als men juistheid wil, ziet men deze in de 2e kolom, die het octaaf verdeelt in 7 grote halve tonen, 3 gemiddelde en 2 kleine*) ... het oor kan het verschil ervan zo goed als niet opmerken.   *)  Dat zijn de op zeer weinig na correcte getallen (resp. met gelijke en met ongelijke halve tonen): 100000, 105946, 112246, 118921, 125993, 133481, 141422, 149830, 158741, 168179, 178172, 188771, 200000. 100000, 106666, 112500, 120000, 125000, 133333, 140947, 150000, 160000, 166666, 177777, 187500, 200000.

  Elders in Harmonie Universelle ('Livre Premier des Instrumens', Prop. 14) leert Mersenne ons dat de aangehaalde 13 evenredige getallen voor hem zijn berekend door "Monsieur Beaugrand, tres excellent Geometre". Hij spreekt op deze plaats over de mogelijkheid ze te gebruiken "om de hals van de Luit te verdelen, van de Viool, van de Cistre enz.". Verder, op p. 21 van 'Nouvelles Observations Physiques & Mathematiques', geeft Mersenne (8e Observation) de "11 getallen die de 11 middelevenredigen vertegenwoordigen ... die de heer Gallé heeft berekend", te weten 100000000000, 94387431198, 89090418365 ... 50000000000.
Op p. 384 (Prop. 38 van 'Livre Sixiesme des Orgues' — instrumenten waarover het ook gaat, Prop 45 van p. 408, over "verdelen van het octaaf ... in twaalf gelijke halve tonen" —) schreef Mersenne:

De heer Boulliau, een van de uitnemendste Astronomen van onze eeuw ... heeft mij een Harmonische tabel gegeven die het verdient in deze verhandeling te worden opgenomen, omdat hij de gehele Muziektheorie bevat ... hij bevat de genoemde wortels zo nauwkeurig, dat de breuken die volgen op de hele getallen gaan tot de eerste en tweede onder­verdelingen.

In feite laat de nauwkeurigheid iets te wensen over. Het gaat om 11 meetkundige middel­evenredigen tussen de getallen 2 en 4, geschreven in het sexagesimale stelsel [60-tallig], te weten 2°7′12″, 2°14′52″, 2°22′33″, 2°31′12″, 2°40′5″, 2°49′39″, 2°59′32″, 3°10′5″, 3°21′50″, 3°33′43″, 3°46′20″ [kolom VI in de tabel op p. 385]. Zie over de getallen van Beaugrand, Boulliau, en Gallé: Aanhangsel II, p. 171 hierna [daar ook meer over Jean Gallé].

  Wat betreft de Aristoxenianen, Mersenne spreekt ervan o.a. op p. 67 en 70 van 'Livre Second des Instrumens' (Prop. 7) in deze termen:

... aangezien Aristoxenos en zijn leerlingen de toon hebben verdeeld in 2 gelijke halve tonen ... en verscheidenen deze verdeling gebruiken op de hals van de Luit en van de Viool, wil ik hier de praktijk van deze verdeling tonen ... Degenen die andere manieren wensen om het Octaaf te verdelen, en de hals van de Luit, en van Violen in 12 gelijke halve tonen, kunnen Zarlino bekijken in het 4e boek van zijn Supplement, hoofdstuk 30, waar hij deze verdeling toepast op de hals van de Luit, en Salinas, zijn tijdgenoot, in zijn 3e boek hoofdstuk 31, zodat het bijna 60 jaar geleden is dat de uitvinding van gelijke halve tonen van Aristoxenos vernieuwd is door deze twee Musici.

Zie over Zarlino en Salinas p. 45 hierna. Raadpleeg ook noot 1 van p. 171.

  [ T. 21, Add., p. 187:]  Huygens heeft niet aangehaald: D. Rembrandtsz. van Nierop, Wis-konstige Musyka ..., Amst. 1659 (txt), waarin men dezelfde kritiek op de theorie van Stevin vindt in de deel 4, VII. 'De redens der toonen na Symon Stevin', VIII, 'Aenmerckinge op de redens der toonen van Symon Stevin' [met op p. 67: "hoe dat 'er meer slagen gelijck vallen / hoe dat de mee-klanck volmaeckter of vermaeckelijcker is"].
Het is waar dat we niet kunnen bewijzen dat Huygens dit werkje kende.
[ Onderdeel van Mathematische Calculatie, Amst. 1659 (zie titelpagina), en dit komt voor in de veiling­catalogus van Huygens' boeken, 1695, p. 13, octavo 53.]

  ¹⁰)  Huygens komt kort terug op deze kwestie in het Stuk van p. 168.
[ App. I bij 'Nouveau Cycle', p. 169: "Dat zonder twijfel de verdelingen van 3 tot 2, 4 tot 3, 5 tot 4, 6 tot 5 de beste consonanten geven die er kunnen zijn. Tegen Stevin."]
Een brief aan S. Stevin van Abraham Verheijen, organist te Nijmegen — die gevoegd was bij het in de vorige noot genoemde manuscript en gepubliceerd door Bierens de Haan samen met het manuscript — laat zien dat de schrijver zijn instemming betuigt met de theorie van Stevin. In de vorige noot heeft men gezien dat Beeckman gedurende verscheidene jaren dezelfde mening had.
  We merken op dat Stevin nog niet wist, zoals Huygens, dat de trillings­frequenties omgekeerd evenredig zijn met de lengten van de snaren (van dezelfde aard en gelijk gespannen). Het moment waarop Beeckman ophield Stevins theorie te geloven moet geweest zijn toen hij besefte dat dit zo is (zie noot 1 van p. 364 van T. 19).

  Men bevindt dat sommige consonanten aangenamer zijn dan andere, en dat die het meest behagen die zijn, waarvan de slagen het vaakst tegelijk komen, met uitzondering echter van eenstemmigheid, waarvan alle slagen tegelijk komen en die

  Behalve die wordt de 12, of de 5 boven het octaaf, het aangenaamst bevonden, waarvan de verhouding is van 3 tot 1, zodat bij elke slag van de lucht bij de lage toon, de hoge er 3 maakt, terwijl bij de 5e de drie slagen van de hoge toon tegelijk komen met slechts 2 slagen van de lage toon, en dat maakt dat de 12 aangenamer is dan de 5. Na de 12e is de volgende in zoetheid de 17e of de grote terts boven

  Wanneer je volgens deze stelregel de kwart vergelijkt met de grote terts, zou je zeggen dat de laatste minder aangenaam zou moeten zijn dan de kwart, want elke 3e slag komt tegelijk met een 4e in de kwart; en in de terts komt elke 4e slag tegelijk met een 5e. En toch schijnt de kwart het minst goed van de twee.
Hetzelfde is in het algemeen overal te zien, dat van twee consonanten die, waarvan de eerste of tweede repliek een veelvoud wordt, beter schijnt dan de andere. En de reden lijkt te zijn dat men bij het horen van een toon veronderstelt, en op de een of andere manier lijkt te horen, het hogere octaaf ervan, of zelfs het dubbel-octaaf. En men hoort het werkelijk bij het aanslaan van een snaar, of een grote klok, en zelfs de 12e en de 17e ¹²).
Zodat men, zoals de replieken van deze consonanten een veelvoud van elkaar zijn, waarvan de samenkomsten van slagen veelvuldiger zijn dan de andere, de consonantie zelfs inschat naar het mooi klinken van deze replieken.
Zo komt het dus, aangezien de replieken van de terts de 10e en de 17e zijn, waarvan de ene bij 2 slagen van het lage geluid en de andere er bij elke 5 heeft van het hoge geluid, die daarom beter zijn dan de kwart, waarin het samenkomen slechts gebeurt om de 3 slagen van het lage geluid, en evenzo bij alle replieken ervan; dat men de grote terts zelf beter vindt dan de kwart ¹⁴).

  De voorkeur voor andere consonanten is volgens dezelfde regels te onderzoeken, en het is nuttig deze graden van mooi klinken te kennen, hoewel het waar is dat niet alle smaken geheel overeenstemmen in dit oordeel. Wat wel duidelijk blijkt

  Het is hierbij goed te onderzoeken of er niet andere consonanten zijn dan die we hierboven hebben bepaald en of er enige reden is om het te bevestigen. Want misschien zouden wij dezelfde fout kunnen maken als de ouden.

  De verhoudingen van getallen die de consonanten samenstellen worden geacht te zijn die van een van de getallen 1, 2, 3, 4, 5, 6, tot een ander van deze zelfde rij, daarbij ook inbegrepen het dubbele en de helft van deze getallen of zelfs andere veelvouden en getallen deelbaar door 2, wat niets anders doet dan de consonant toevoegen aan een of meer octaven, ofwel deze er afnemen.
Het getal 7 hoort hier niet bij, noch een ander priemgetal of getal dat is samengesteld uit priemgetallen ¹⁶). En sommigen ¹⁷) schrijven dit toe aan de volmaaktheid van het getal 6, dat ze daarom harmonisch noemen. Toch zal men alles welbeschouwd en zonder vooroordeel vinden dat het getal 7, vergeleken met andere, ook in staat is een consonant voort te brengen ¹⁸), maar dat de voortgebrachte consonanten niet passen bij de al vastgestelde, en dat ze niet zo goed zijn ¹⁹).

Trompet-tonen, 1-8

  Daarvan komt het dat men ook van Ut naar Re gaat als eerste interval, wanneer men naar de kwint bij Sol gaat, of alleen naar de kwart bij Fa, omdat Re - Fa een consonant is, te weten de kleine terts van 6 tot 5. Want het zou tegen de borst stuiten als men in plaats van te zingen Ut Re Mi Fa, een andere toon zou willen invullen in plaats van Re, die niet consonant zou zijn met Fa noch met een van de andere tonen.
Ik zeg noch met een van de andere, omdat men ervoor zou kunnen invullen Ut, en zingen Ut Ut Mi Fa, omdat Ut met Mi de kleine terts maakt. Maar men gaat niet naar deze chromatische toon, zowel om de kleinheid van het interval Ut - Ut als omdat de Ut helemaal niet consonant is met de volgende tonen of met de Re; want deze maakt de kwart tegen de Sol, de kwint tegen de La en de sext tegen de Ci [Si]. Maar Ut alleen de sext tegen La.

  Het is gemakkelijk te bewijzen met dergelijke redenen als de zojuist genoemde, waarom

  Onze toegevoegde halve tonen, die men chromatisch ⁴) kan noemen, zijn eveneens gebaseerd op cononsanten. Want Ut - Mi maakt de kleine terts, Mi - Sol de grote terts, Mi - Ci de kwint, Mi - Ut ² de grote sext, evenzo Re Fa de grote terts, Fa - La de kleine terts, Fa - Ci de kwart, Fa - Re de kleine sext. Verder Mi - Sol de grote terts, Sol - Ci de kleine terts, Sol - Mi de kleine sext.