In vertaling , In het Nederlands , Tekeningen
Œuvres XIXOeuvres Complètes de Christiaan Huygens, T. XIX (dbnl)Mechanica en natuurkunde 1666 - '95 In vertaling

|
In het Nederlands
| 142 | Diepte van de zee | 27 aug. 1690 | |
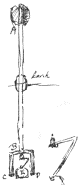 Inventie om de onpeilbare dieptens van de zee te meten en met eenen kennis te krijgen van de grondt, als sand, schelpen, &c.
Inventie om de onpeilbare dieptens van de zee te meten en met eenen kennis te krijgen van de grondt, als sand, schelpen, &c. Men kan maecken dat de stock met de steen daer aen, even soo veel in 't water neerwaerts weeght, als sonder de steen opwaerts, maer dit is niet noodtsaeckelyck ... AB stock van 10 à 12 voet. CBD vorck van hout, tusschen welcke hanght de steen E aen ijseren haeck van figuer als een 7. de eynden C en D onder met keersmeer bestreecken, om te sien wat grondt. Het gewight E de grondt ontmoetende soo sal den haeck los gaen om dat hij nae d'een sij weeght, en omdat de drift van de stock AB neerwaerts noch een weijnigh dueren sal. ... In de figuur: "korck" [kurk]. Robert Hooke had in 1663 zo'n toestel bedacht voor dieptemeting zonder lijn en bovendien een emmer (aan een lijn) om water van elke diepte te kunnen ophalen, zie Th. Birch, The history of the Royal Society (1756) I, 307-308, 'An appendix to the Directions for Seamen, bound for far voyages' in Phil. Trans. feb. 1666 (Num. 9; note in Num. 10: p. 178), het 'Extrait' daarvan in Journal des sçavans, 1666, p. 218 (3 mei) en een reactie van Pierre Petit op p. 247 (24 mei), en tenslotte het commentaar hierop in Phil. Trans., 1666, Numb. 13, p. 228. Het toestel werd in 1667 genoemd door Adr. Auzout in een lijst van instrumenten, mee te nemen op een reis naar Madagascar [^]: "Toestellen om de diepte van de zee te peilen en om water op te halen vanaf de bodem van de zee" en "Men moet vaak de zeeën peilen waar men over gaat met het toestel van M. Hook" (Registres de l'Acad. I, 39 en 49). Uitleg met figuur ook in Simon Witgeest, Het natuurlyk tover-boek, 1684, p. 28 en p. 183. [ Vgl. X, 237, brief van broer Constantijn uit Engeland (26 jan. 1692): Edmond Halley had meer dan een uur in een duikerklok gezeten op een diepte van 60 voet.] | |||
Tekeningen
| 32 | Simpelste machine | 1676 | |
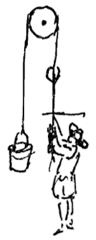
En er kan hier niets anders aan toegevoegd worden dan een gewicht aan het touw, dat evenwicht maakt met de lege emmer, of ook nog iets waardoor de emmer niet terug kan vallen.
| |||
| 122 | Kracht van stromend water | 1669 | |

|
... te meten ... hoeveel gewicht een bepaalde breedte aan water, dat met een bepaalde snelheid stroomt, kan optillen tot een bepaalde hoogte. En omdat het effect van de druk gelijk is, of het water nu tegen een voorwerp komt, of dat het voorwerp met dezelfde snelheid in stilstaand water beweegt ... [beweging is immers relatief!]. [ HUG 2, 78v: originele tekening (met nog een mast op de rechterkant), samen met de hierna volgende. Nog zo'n tekening staat op HUG 26, 107v, in het net en nu zonder mast.]
| |||
126 | Proef op de Seine | 1669 | |
|
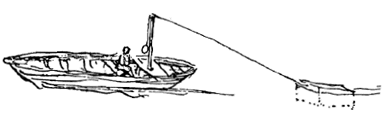
... een blok eikenhout, een voet in het vierkant, 2 voet hoog. Men heeft de boot stilgelegd in het stromende water, en het genoemde stuk hout eraan blootgesteld ... zoveel gewicht als opwoog tegen het trekken van het blok ... Om vervolgens de stroomsnelheid te meten liet men het blok met het water meegaan, en tegelijk liet men een slinger met halve seconden bewegen ...
| ||||
| 436 | Lichtbreking | 1678 | ||
| ||||
| 474 | Lichtgolven | 1690 | ||
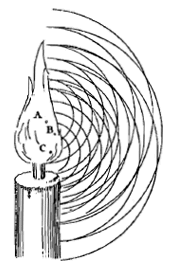
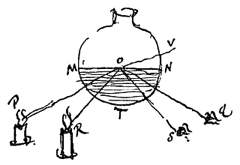
... dat elk plekje van een lichtgevend voorwerp, zoals de Zon, een kaars, of een gloeiende kool, zijn eigen golven voortbrengt, waarvan dit plekje het middelpunt is. Zoals in een kaarsvlam: als de punten A, B en C worden onderscheiden zijn de concentrische cirkels, rondom elk van deze punten beschreven, een weergave van de golven die eruit voortkomen. En men moet er evenzo bedenken rondom elk punt van het oppervlak, en een deel van het binnenste van deze vlam. Maar aangezien de stootjes in het midden van deze golven geen regelmatige opeenvolging hebben, moet men zich ook niet voorstellen dat de golven zelf elkaar met gelijke afstanden opvolgen ... In: Traité de la Lumière (Leiden 1690), p. 15 (mijn vertaling). Verhandeling over het licht, vertaling D. Eringa (Utr. 1990).
| ||||
| 475 | Voortplanting | 1690 | ||
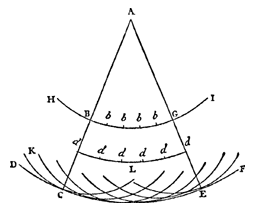
Bij de uitbreiding van deze golven is nog te overwegen, dat elk deeltje van de materie, waarin een golf zich voortplant, zijn beweging niet allen moet doorgeven aan het volgende deeltje, dat ligt op de vanuit het lichtpunt getrokken rechte lijn; maar dat het noodzakelijkerwijze ook enige beweging geeft aan alle andere die eraan raken, en die zich verzetten tegen zijn beweging. Zodat rondom ieder deeltje een golf moet ontstaan waarvan dit deeltje het middelpunt is. ... Dit is het 'Beginsel van Huygens'. | ||||
| | ||||
| 517 | IJslands kristal | 1690 | ||
|
'De l'estrange refraction du cristal d'Islande', Over de vreemde breking van IJslands kristal, is de titel van hoofdstuk 5 van Traité de la Lumière. Het beslaat bijna de helft van het boekje (p. 48-101 van 124) en verklaart voor het eerst de dubbele breking, ontdekt door Eramsus Bartholin. Huygens had de verklaring gevonden op 6 augustus 1677 [<]. Bovendien had hij ontdekt dat de twee componenten van een dubbel gebroken straal zich niet nog eens verdubbelen in een tweede stuk IJslands kristal. Hiervan staat een tekening op p. 89 (Verhandeling over het licht, Utr. 1990, naast p. 195). Zo'n stuk IJslandspaat daarop, uitsnede van foto: |
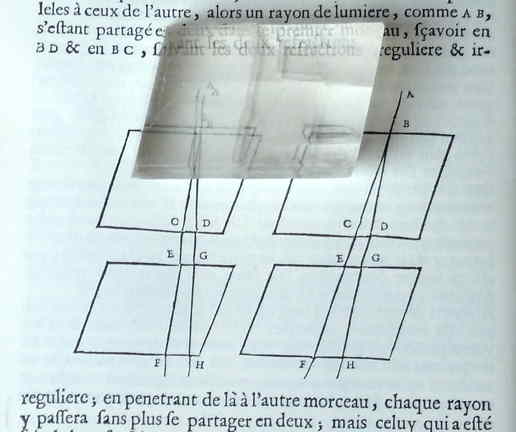
Onleesbare tekst bovenaan:
"... partagé en deux dans le premier morceau, ..."
"... BC, suivant les deux refractions, reguliere ..."
Vertaling (van mij): |
|
... als dan een lichtstraal, zoals AB, zich heeft verdeeld in tweeën in het eerste stuk, te weten in BD en in BC, volgens de twee brekingen, de regelmatige en de on- regelmatige; zal vandaar doordringend in het andere stuk, elke straal er doorgaan zonder zich verder in tweeën te verdelen ... |
|
Vertaling (Dieuwke Eringa, 1990): |
|
... dringt een lichtstraal, zoals AB, vandaar door naar het tweede stuk volgens de beide typen breking, de gewone en de ongewone. Elke straal komt daarin zonder zich opnieuw te splitsen. |
Home | Huygens | uit Oeuvres XIX (top) | Sommaire , Inhoud