|
existant, modo leges positas sequaris & sinus 30 gr. statuatur dimidius ejus qui ad 90 gr. pertinet, res experiunti erit haud difficilis.
Quamobrem ad canonis sinuum concenturiationem parata & facilis est nobis via: Nam si prior ordo per scrupulorum paria instituatur, ut 2, 4, 6, 8, 10, alter loca intermedia explebit 1, 3, 5, 7, 9. atque ita porro; res ex antecedenbus manifesta est, ut 2700 additiones reciprocando, tam acccuratos canones exhibere possis quam tibi erit collibitum: atqui cum radius hic alius sit, quam vulgo usitatus, hos sinus ad millesimas vel divisionis vel multiplicationis via reduces.
Verum enimvero ne adeo vastum pelagus nullo duce, & quasi fortuito ingrediaris, quamvis etiam ita ad portum destinatum occultis legibus necessario proveharis; tamen expediet aliquam adhibere huic operi cynosuram, quo facilius ex his tricymiis*) & undarum agitationibus molestis, navem in portu incolumem constituas. Oportunum itaque erit saltem singulorum graduum, aut etiam quod non improbem semissium, sinus jam ante legittimos ut minimum ad radium quatuor notarum invenisse, atque inde secundum hanc differentiam proportionaliter sinuum quantitatem per bina scrupula ordinare. Hac enim via, secunda additione facile ad radium sex aut septem notarum legittimos sinus exsculpes, & si eandem vicissitudinem secundo iteres, jam ad 10 aut 11 notas facile pervenies; consensum arguet sinus 90 gr. cum sinu 30 gr. comparatus, Sed priusquam hic manum tollam de tabula etiam lateris cujuscunque polygoni inventionem, mihi hac eadem via docendus es: quam utique inter extrema hujus theorematis merita, haud reponendam censeo.
[ *) Gr. 'trikumia': driedubbele golf, stortvloed. Cynosura: dog's tail.]
|

 [ *) In de figuur van p. 8 is de genoemde boog ei veel groter.
[ *) In de figuur van p. 8 is de genoemde boog ei veel groter. 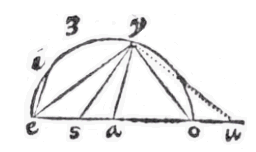
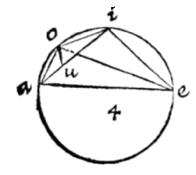

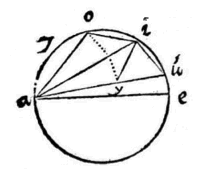
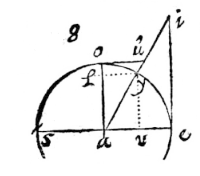
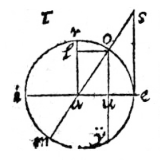
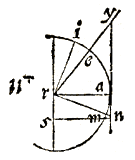 DETUR in hoc diagrammate peripheria ea, ejusque secans ry, tangens ya; dimidium vero complementum arcus ei seu arcus am, ejusque tangens an; dico lineam ry aequari lineae yn: cum enim irm sit quadrans circuli, & angulus rectus ad r, erit ire compl. anguli yrm, & aequale angulo arm ex structura; similiter ducta perpendiculari ad punctum n; angulus rns, aequalis erit angulo ire, seu arn ob parallelismum linearum ra, sn;
DETUR in hoc diagrammate peripheria ea, ejusque secans ry, tangens ya; dimidium vero complementum arcus ei seu arcus am, ejusque tangens an; dico lineam ry aequari lineae yn: cum enim irm sit quadrans circuli, & angulus rectus ad r, erit ire compl. anguli yrm, & aequale angulo arm ex structura; similiter ducta perpendiculari ad punctum n; angulus rns, aequalis erit angulo ire, seu arn ob parallelismum linearum ra, sn; 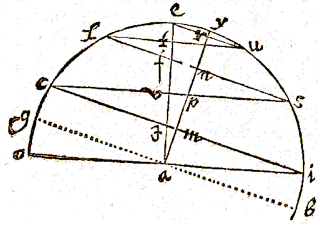

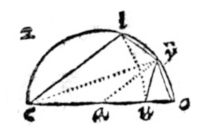
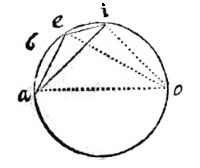
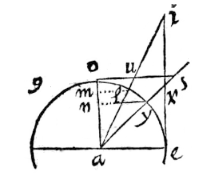
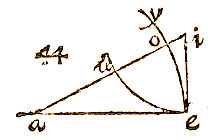
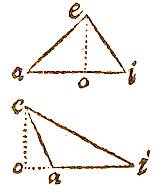
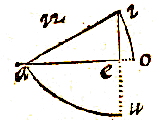 UT hic vides, si centro a intervallo hypotenusae ai describatur peripheria io, tum ei erit sinus anguli acuti iao. si ex acuto i desribatur peripheria au, tum ae fiet sinus anguli aie. res ex sinuum definitione est manifesta.
UT hic vides, si centro a intervallo hypotenusae ai describatur peripheria io, tum ei erit sinus anguli acuti iao. si ex acuto i desribatur peripheria au, tum ae fiet sinus anguli aie. res ex sinuum definitione est manifesta. 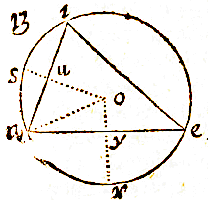 Trianguli latera sinibus oppositorum angulorum sunt proportionalia.
Trianguli latera sinibus oppositorum angulorum sunt proportionalia. 
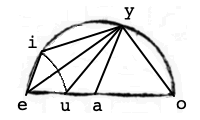
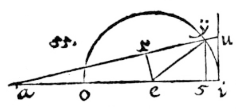
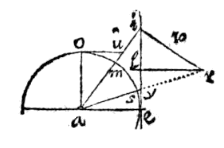
 ET hoc quoque ex primi libri theorematis est perspicuum. Sit aei triangulum rectangulum, ergo si ex angulo a intervallo ae, circulus ey describatur, fiet ei tangens peripheriae eo per
ET hoc quoque ex primi libri theorematis est perspicuum. Sit aei triangulum rectangulum, ergo si ex angulo a intervallo ae, circulus ey describatur, fiet ei tangens peripheriae eo per 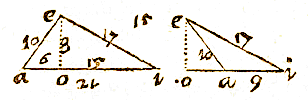
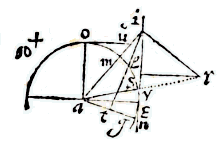
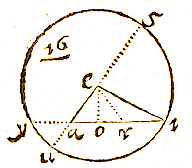 ut hic triangulum esto datum aei: ex angulo a [e], radio cruris majoris ei describatur circulus iys, & continuentur basis ia, & crus minus ae. rectangulum uas, aequatur rectangulo iay, quare ay addita ad ai dabit totam iy, cujus dimidium io, distantia a crure majori. rursum ya ri aequentur, reliquae ar dimidium ao distantia erit a crure minori.
ut hic triangulum esto datum aei: ex angulo a [e], radio cruris majoris ei describatur circulus iys, & continuentur basis ia, & crus minus ae. rectangulum uas, aequatur rectangulo iay, quare ay addita ad ai dabit totam iy, cujus dimidium io, distantia a crure majori. rursum ya ri aequentur, reliquae ar dimidium ao distantia erit a crure minori. 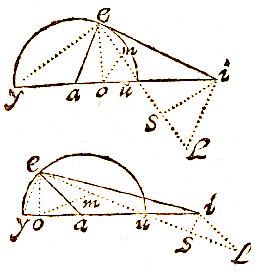 Sit igitur triangulum aei, & anguli a basis ei. perpendicularis à vertice eo, apotome ao, & ay, au sint cruri ae aequales, connexis ye eu angulus yeu in semicirculo rectus erit:
Sit igitur triangulum aei, & anguli a basis ei. perpendicularis à vertice eo, apotome ao, & ay, au sint cruri ae aequales, connexis ye eu angulus yeu in semicirculo rectus erit:  Ut summa sinuum, ad differentiam eorundem, ita tangens dimidiae summae peripheriarum, ad tangentem dimidiae, earundem differentiae.
Ut summa sinuum, ad differentiam eorundem, ita tangens dimidiae summae peripheriarum, ad tangentem dimidiae, earundem differentiae. 
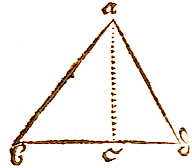 IN triangulo bad, detur basis bd 24 decemp. angulus abd 42 gr. 30 scr. & area ipsius 140 decemp. quaerantur vero latera singula, ba, ad;
IN triangulo bad, detur basis bd 24 decemp. angulus abd 42 gr. 30 scr. & area ipsius 140 decemp. quaerantur vero latera singula, ba, ad; 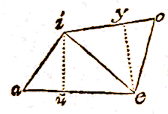 SIt in proposito diagrammate ae 54, eo 32, oi 46, ia 28 decempedarum, angulus iae 67 gr. 30 scr.
SIt in proposito diagrammate ae 54, eo 32, oi 46, ia 28 decempedarum, angulus iae 67 gr. 30 scr. 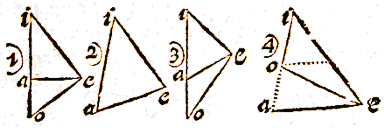
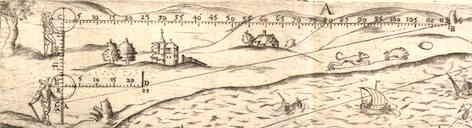
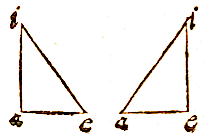
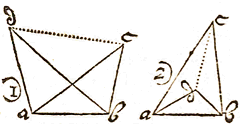 SInt data duo loca in primo diagrammate cd, stationes duae alibi extrà lineam quae illa connectit, in a & b, distantiâ 244 decempedarum, 6 pedum, sic 244.6. observatis angulis dba 36 gr. 15 scr. dab, 124 gr. 20 scr. Item cab 40 gr. 49 scr. & abc 112 gr. 30 scr. Investigabitur linea cd hoc modo:
SInt data duo loca in primo diagrammate cd, stationes duae alibi extrà lineam quae illa connectit, in a & b, distantiâ 244 decempedarum, 6 pedum, sic 244.6. observatis angulis dba 36 gr. 15 scr. dab, 124 gr. 20 scr. Item cab 40 gr. 49 scr. & abc 112 gr. 30 scr. Investigabitur linea cd hoc modo:  Tertiò si stationes dentur ab utraque parte lineae cd, ita ut ba eandem intersecet; tunc quidem si detur accessu in e, utere
Tertiò si stationes dentur ab utraque parte lineae cd, ita ut ba eandem intersecet; tunc quidem si detur accessu in e, utere 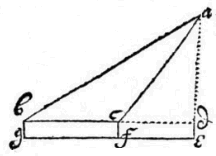
 Verumenimvero si res mensuranda ita sita sit, ut nullo modo basis inter duas stationes, tendere possit in directum perpendiculi, sed eandem transversim assumere liceat ad libitum; tum instrumento ita inclinato (in praesenti diagrammate) ut respondeat plano trianguli abc hoc est ut per dioptras simul intueri possis rei mensurandae cacumen b, & alteram stationem a, dimetire primò angulum aeb, qui hoc casu detur 57 gr. 30 scr. inde simili modo angulum bae, qui sit 69 gr. 42 scr. & tunc datâ basi ae 30 decemp. cum tertio angulo abe 52 gr. 48 scr. dic ut suprà
Verumenimvero si res mensuranda ita sita sit, ut nullo modo basis inter duas stationes, tendere possit in directum perpendiculi, sed eandem transversim assumere liceat ad libitum; tum instrumento ita inclinato (in praesenti diagrammate) ut respondeat plano trianguli abc hoc est ut per dioptras simul intueri possis rei mensurandae cacumen b, & alteram stationem a, dimetire primò angulum aeb, qui hoc casu detur 57 gr. 30 scr. inde simili modo angulum bae, qui sit 69 gr. 42 scr. & tunc datâ basi ae 30 decemp. cum tertio angulo abe 52 gr. 48 scr. dic ut suprà 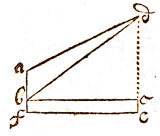 Quapropter in diagrammate sequenti sit alt. mensuranda ed, prima statio in f, instrumentum a. in b, & observato angulo dbc 40 gr. 32 scr. sit secunda statio in a ibique rursus observato angulo quo linea ad, supra planum horiz. assurgit, addo ipsi 90 gradus ut habeam obtusum dab, aut sumo ejus complementum ut habeam exteriorem ad a, qui nunc sit 62 gr. 54 scr. ex obtuso itaque, aut exteriore hoc angulo, & dato dbc, inquiro ang. adb qui hic est 13 gr. 16 scr. [26 scr.]
Quapropter in diagrammate sequenti sit alt. mensuranda ed, prima statio in f, instrumentum a. in b, & observato angulo dbc 40 gr. 32 scr. sit secunda statio in a ibique rursus observato angulo quo linea ad, supra planum horiz. assurgit, addo ipsi 90 gradus ut habeam obtusum dab, aut sumo ejus complementum ut habeam exteriorem ad a, qui nunc sit 62 gr. 54 scr. ex obtuso itaque, aut exteriore hoc angulo, & dato dbc, inquiro ang. adb qui hic est 13 gr. 16 scr. [26 scr.] 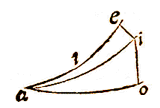
 SIT in apposito diagrammate, k Polus arcticus, aec Æquator, fhi Ecliptica, bed Horizon, hl distantia Solis ab Ariete, puta 60 grad. ejus ascens. recta hm 57 gr. 48 scr. 6 sec. & declin. borea lm 20 gr. 13 scr. 22 sec. altitudo autem Poli Arctici kd 52 gr. 10 scr. 30 sec. quanta est almae Academiae Leydensis: quaeritur he ascensio obliqua loci Solis l;
SIT in apposito diagrammate, k Polus arcticus, aec Æquator, fhi Ecliptica, bed Horizon, hl distantia Solis ab Ariete, puta 60 grad. ejus ascens. recta hm 57 gr. 48 scr. 6 sec. & declin. borea lm 20 gr. 13 scr. 22 sec. altitudo autem Poli Arctici kd 52 gr. 10 scr. 30 sec. quanta est almae Academiae Leydensis: quaeritur he ascensio obliqua loci Solis l;  SIT in apposito diagrammate, Polus arcticus m, antarcticus z, Æquator iqe, Horizon oqh, locus Solis aut stellae s, ejusque parallelus diurnus asp vel usc, Declinatio borea sd vel austrina sr.
SIT in apposito diagrammate, Polus arcticus m, antarcticus z, Æquator iqe, Horizon oqh, locus Solis aut stellae s, ejusque parallelus diurnus asp vel usc, Declinatio borea sd vel austrina sr.  IN adjecto diagrammate, sit e Polus arcticus, o punctum Verticale, agc Æquator, hzi Ecliptica, dgh Horizon, m locus Solis, omp circulus verticalis per locum Solis in Horizontem eductus, & sit exempli gratia arcus be elevatio Poli 52 gr. 10 scr. 30 sec. loci Solis in principio Geminorum, declinatio nm 20 gr. 13 scr. 22 sec. & hora antemeridiana decima, cui cedit arcus an seu ang. aen 30 gr. Quaeritur ang. dop Azimuth Solis à meridie, arcus mp altitudo eius suprà Horizontem, ang. hmo Verticalis & Eclipticae.
IN adjecto diagrammate, sit e Polus arcticus, o punctum Verticale, agc Æquator, hzi Ecliptica, dgh Horizon, m locus Solis, omp circulus verticalis per locum Solis in Horizontem eductus, & sit exempli gratia arcus be elevatio Poli 52 gr. 10 scr. 30 sec. loci Solis in principio Geminorum, declinatio nm 20 gr. 13 scr. 22 sec. & hora antemeridiana decima, cui cedit arcus an seu ang. aen 30 gr. Quaeritur ang. dop Azimuth Solis à meridie, arcus mp altitudo eius suprà Horizontem, ang. hmo Verticalis & Eclipticae. 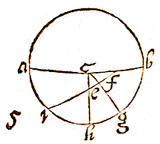 i, Æquator cfg, Verticalis cek, declin. Solis fe, complementum elev. Poli borei ik, depressio Solis sub Horiz. ce.
i, Æquator cfg, Verticalis cek, declin. Solis fe, complementum elev. Poli borei ik, depressio Solis sub Horiz. ce. 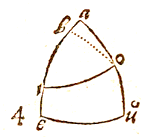

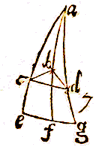 inferior in cornu Capricorni d, Cometa verò c, & per haec loca tres descendant quadrantes adg, abf, ace, tunc connexis cb, bd, cd quaeratur longitudo Cometae in e, & latit. ec his modis
inferior in cornu Capricorni d, Cometa verò c, & per haec loca tres descendant quadrantes adg, abf, ace, tunc connexis cb, bd, cd quaeratur longitudo Cometae in e, & latit. ec his modis 