het voortdurend vermenigvuldigde van de helft met de overige zal zijn 51 935 886 974 519, waarvan de wortel, 7 206 655 vierkante duim, zal zijn het oppervlak van de driehoek, namelijk 720 tienvoet, 66 voet, 55 duim.
Je zou hier ook, met verwaarlozing van duimen in het begin, het oppervlak met minder getallen hebben kunnen vinden, maar die zouden hebben geleid tot een fout in het geringe aantal vierkante voeten.
En daarom zal het hier misschien handig zijn de hoek ioe te vinden, wat in dit geval heel goed te doen is op de tweede manier van prop. 12. Daar immershierboven gegeven is het kwadraat van basis ei, 25427654, waarvan het verschil met de kwadraten van de benen io en oe, 31400060, is 5972346; daarom is tweemaal de rechthoek op de benen io en oe: 29440000.
Dus zal gelden:
zoals tweemaal rechth.
op benen oe, oi,
| tot verschil van
kwadr. benen en basis
| zo is de hele sinus
| | 29440000 | 5972346 | 10000000
|
tot de sinus 2031250, die geeft: 11° 43' 11", en omdat het kwadraat van de basis kleiner is dan de kwadraten van de benen, zal hoek o scherp zijn; en daarom wordt deze zelf gegeven als 78° 16' 59". Dus hier zal in de rechthoekige driehoek eyo, bij gegeven basis eo 32, en de hoek bij o 78° 16' 49", als gevolg van prop. 2, lib. 2, gegeven worden de loodlijn ey:
| zoals de hele sinus,
| tot sinus van hoek o,
| zo is ae, | tot ey
| | 10000000 | 9791527 | 32. 0. 0. | 3133 2886/10000
|
wat vermenigvuligd met de helft van zijde oi, 23, zal geven het oppervlak van driehoek ieo, 720 tienvoet, 65 voet, welke grootte iets verschilt van die hierboven wegens onzekerheid in de berekening.
Verder zal het oppervlak van driehoek iae langs dezelfde weg gegeven worden als 698 tienvoet, 39 voet, 19 duim, of als gevonden is de loodlijn iu, 25 8686/10000, met sinustabellen, en deze vermenigvuldigd is met de helft van basis ae, 27, zal hetzelfde oppervlak zijn 698 tienvoet, 45 voet, 20 duim. En daarom zal het oppervlak van het hele trapezium zijn: of 1419 tienvoet, 5 voet, 74 duim,
|

 [ *) In de figuur van p. 8 is de genoemde boog ei veel groter.
[ *) In de figuur van p. 8 is de genoemde boog ei veel groter. 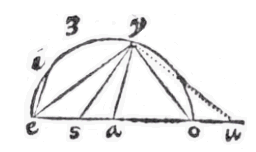

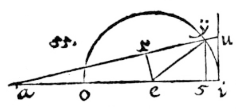
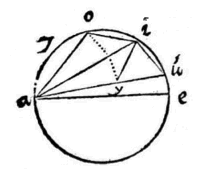
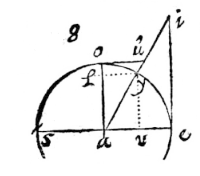
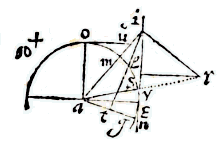
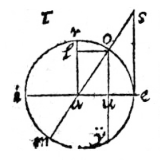
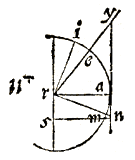 LAAT in deze tekening gegeven zijn de omtrek ea, de secans ry ervan, de tangens ya; en het halve complement van boog ei of boog am, en de tangens daarvan an.
LAAT in deze tekening gegeven zijn de omtrek ea, de secans ry ervan, de tangens ya; en het halve complement van boog ei of boog am, en de tangens daarvan an. 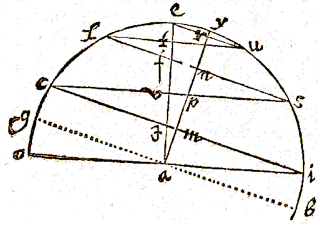

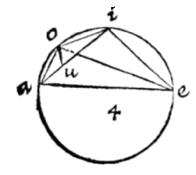
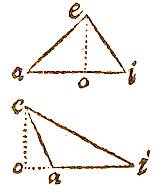
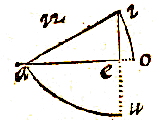 ZOALS je hier ziet, als met middelpunt a en het interval van de hypotenusa ai de omtrek io wordt beschreven, dan zal ei de sinus zijn van de scherpe hoek iao. Als uit de scherpe hoek i de omtrek au beschreven wordt, dan zal ae worden de sinus van de hoek aie. De zaak is duidelijk uit de definitie van de sinus.
ZOALS je hier ziet, als met middelpunt a en het interval van de hypotenusa ai de omtrek io wordt beschreven, dan zal ei de sinus zijn van de scherpe hoek iao. Als uit de scherpe hoek i de omtrek au beschreven wordt, dan zal ae worden de sinus van de hoek aie. De zaak is duidelijk uit de definitie van de sinus. 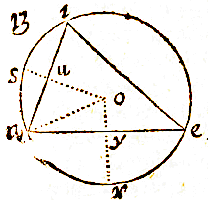 De zijden van een driehoek zijn evenredig met de sinussen van de overstaande hoeken.
De zijden van een driehoek zijn evenredig met de sinussen van de overstaande hoeken. 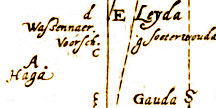
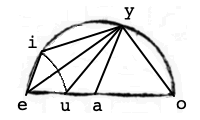
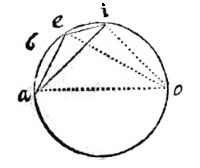
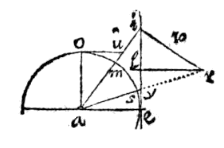
 EN dit is ook te doorzien in een theorema van het eerste boek. Laat aei de rechthoekige driehoek zijn, als dus vanuit de hoek a met interval ae, de cirkel ey wordt beschreven, zal ei de tangens worden van de omtrek eo volgens
EN dit is ook te doorzien in een theorema van het eerste boek. Laat aei de rechthoekige driehoek zijn, als dus vanuit de hoek a met interval ae, de cirkel ey wordt beschreven, zal ei de tangens worden van de omtrek eo volgens 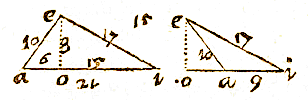
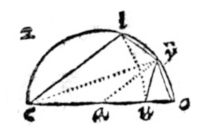
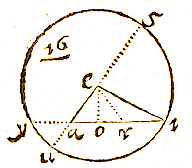 Zoals hier een driehoek aei gegeven kan worden: laat vanuit de hoek e, met als straal het grootste been ei, de cirkel iys beschreven worden, en de basis ia verlengd; en het kleinste been is ae
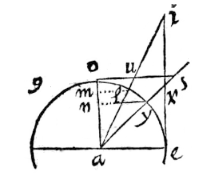
Zoals hier een driehoek aei gegeven kan worden: laat vanuit de hoek e, met als straal het grootste been ei, de cirkel iys beschreven worden, en de basis ia verlengd; en het kleinste been is ae 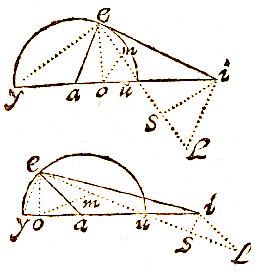 Laat er dus een driehoek aei zijn, van hoek a de basis ei; de loodlijn eo uit de top, het afgesneden segment ao, en laat ay en au gelijk zijn aan been ae; als getrokken worden ye en eu, zal de hoek yeu in een halve cirkel recht zijn.
Laat er dus een driehoek aei zijn, van hoek a de basis ei; de loodlijn eo uit de top, het afgesneden segment ao, en laat ay en au gelijk zijn aan been ae; als getrokken worden ye en eu, zal de hoek yeu in een halve cirkel recht zijn.  Zoals de som van de sinussen is tot het verschil ervan, zo is de tangens van de helft van de som van de omtrekken, tot de tangens van de helft van het verschil ervan.
Zoals de som van de sinussen is tot het verschil ervan, zo is de tangens van de helft van de som van de omtrekken, tot de tangens van de helft van het verschil ervan. 
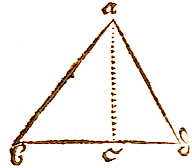 IN de driehoek bad zij gegeven de basis bd, 24 tienvoet, de hoek abd, 42° 30', en het oppervlak ervan, 140 tienvoet. En gevraagd worden de zijden ba en ad afzonderlijk.
IN de driehoek bad zij gegeven de basis bd, 24 tienvoet, de hoek abd, 42° 30', en het oppervlak ervan, 140 tienvoet. En gevraagd worden de zijden ba en ad afzonderlijk. 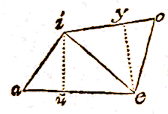 LAat in de voorgestelde tekening ae zijn 54 tienvoet, eo 32, oi 46, ia 28, en hoek iae 67° 30'.
LAat in de voorgestelde tekening ae zijn 54 tienvoet, eo 32, oi 46, ia 28, en hoek iae 67° 30'. 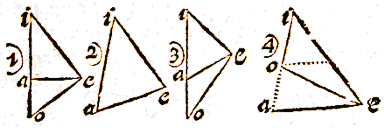
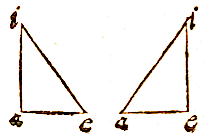
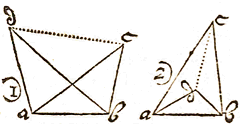 LAat gegeven zijn twee plaatsen in de eerste tekening c en d, en elders twee standplaatsen buiten de lijn die de eerste verbindt, in a en b, met een afstand van 244 tienvoet, 6 voet, zo: 244.6. Als waargenomen zijn de hoeken dba 36° 15' en dab 124° 20;. Evenzo cab 40 ° 49' en abc 112° 30'.
LAat gegeven zijn twee plaatsen in de eerste tekening c en d, en elders twee standplaatsen buiten de lijn die de eerste verbindt, in a en b, met een afstand van 244 tienvoet, 6 voet, zo: 244.6. Als waargenomen zijn de hoeken dba 36° 15' en dab 124° 20;. Evenzo cab 40 ° 49' en abc 112° 30'. 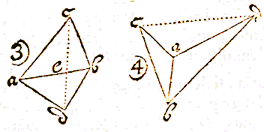 Ten derde, als de standplaatsen gegeven worden aan weerskanten van de lijn cd, zodat ba deze snijdt; dan kun je natuurlijk, als er toegang is tot e,
Ten derde, als de standplaatsen gegeven worden aan weerskanten van de lijn cd, zodat ba deze snijdt; dan kun je natuurlijk, als er toegang is tot e, 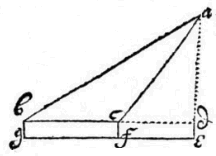
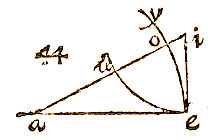
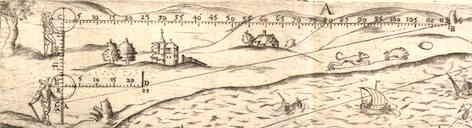
 Echter, als het te meten object zo gelegen is, dat de basis tussen twee standplaatsen op geen enkele manier in de richting van de loodlijn kan liggen, maar deze naar believen dwars kan worden genomen, houd dan het instrument zodanig hellend (in de weergegeven tekening) dat het overeenkomt met de vlakke driehoek abc, dat wil zeggen dat je door de vizieren tegelijk kunt zien de top b van het te meten object, en de andere standplaats a; meet eerst hoek aeb, die in dit geval wordt gegeven als 57° 30', en daarna op dezelfde manier hoek bae, die kan zijn 69° 42'.
Echter, als het te meten object zo gelegen is, dat de basis tussen twee standplaatsen op geen enkele manier in de richting van de loodlijn kan liggen, maar deze naar believen dwars kan worden genomen, houd dan het instrument zodanig hellend (in de weergegeven tekening) dat het overeenkomt met de vlakke driehoek abc, dat wil zeggen dat je door de vizieren tegelijk kunt zien de top b van het te meten object, en de andere standplaats a; meet eerst hoek aeb, die in dit geval wordt gegeven als 57° 30', en daarna op dezelfde manier hoek bae, die kan zijn 69° 42'. 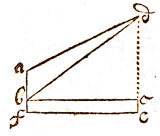 Laat daarom in de volgende tekening de te meten hoogte zijn ed, de eerste standplaats in f, een astronomisch instrument in b, en als hoek dbc is waargenomen als 40° 32', laat dan de tweede standplaats zijn in a en als daar weer is waargenomen de hoek waarmee de lijn ad boven de horizon oprijst, tel ik erbij op 90° om de stompe hoek dab te krijgen, of ik neem het complement ervan om de buitenhoek bij a te krijgen, die nu kan zijn 62° 54'. Dus met de stompe hoek, of met deze buitenhoek, en de gegeven dbc zoek ik hoek adb die hier 13° 16' [26'] is .
Laat daarom in de volgende tekening de te meten hoogte zijn ed, de eerste standplaats in f, een astronomisch instrument in b, en als hoek dbc is waargenomen als 40° 32', laat dan de tweede standplaats zijn in a en als daar weer is waargenomen de hoek waarmee de lijn ad boven de horizon oprijst, tel ik erbij op 90° om de stompe hoek dab te krijgen, of ik neem het complement ervan om de buitenhoek bij a te krijgen, die nu kan zijn 62° 54'. Dus met de stompe hoek, of met deze buitenhoek, en de gegeven dbc zoek ik hoek adb die hier 13° 16' [26'] is . 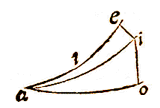
 LAAT in de bijgevoegde tekening, k de Noordpool zijn, aec de Hemelevenaar, fhi de Ecliptica, bed de Horizon, hl de afstand van de Zon tot het
LAAT in de bijgevoegde tekening, k de Noordpool zijn, aec de Hemelevenaar, fhi de Ecliptica, bed de Horizon, hl de afstand van de Zon tot het  LAAT in de tekening hiernaast de Noordpool zijn m, de Zuidpool z, de Hemelevenaar iqe, de Horizon oqh, de plaats van de Zon of een ster s, en de dagelijkse parallel ervan asp of usc, de Declinatie noordelijk sd of zuidelijk sr.
LAAT in de tekening hiernaast de Noordpool zijn m, de Zuidpool z, de Hemelevenaar iqe, de Horizon oqh, de plaats van de Zon of een ster s, en de dagelijkse parallel ervan asp of usc, de Declinatie noordelijk sd of zuidelijk sr.  IN de bijgevoegde tekening zij e de Noordpool, o het zenit, agc de hemelevenaar, hzi de Ecliptica, dgh de Horizon, m de plaats van de Zon, omp de vertikale cirkel op de Horizon getrokken door de plaats van de Zon, en bijvoorbeeld de boog be de Poolshoogte 52° 10' 30"; plaats van de Zon in het begin van Tweelingen, declinatie nm 20° 13' 22", en uur van de dag 10 uur voor de middag, wat geeft voor boog an of hoek aen 30°.
IN de bijgevoegde tekening zij e de Noordpool, o het zenit, agc de hemelevenaar, hzi de Ecliptica, dgh de Horizon, m de plaats van de Zon, omp de vertikale cirkel op de Horizon getrokken door de plaats van de Zon, en bijvoorbeeld de boog be de Poolshoogte 52° 10' 30"; plaats van de Zon in het begin van Tweelingen, declinatie nm 20° 13' 22", en uur van de dag 10 uur voor de middag, wat geeft voor boog an of hoek aen 30°. 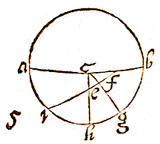 Hemelevenaar cfg, Vertikale cirkel cek, declinatie van de Zon fe, complement van de noordelijke Poolshoogte ik, diepte van de Zon onder de Horizon ce.
Hemelevenaar cfg, Vertikale cirkel cek, declinatie van de Zon fe, complement van de noordelijke Poolshoogte ik, diepte van de Zon onder de Horizon ce. 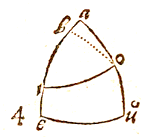

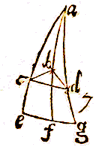 de lagere in de hoorn van Steenbok d en de Komeet c; en laat door deze drie plaatsen neerdalen de kwadranten adg, abf, ace, dan kan na verbinding cb, bd, cd worden gezocht de lengte van de Komeet in e, en de breedte ec op de volgende manieren.
de lagere in de hoorn van Steenbok d en de Komeet c; en laat door deze drie plaatsen neerdalen de kwadranten adg, abf, ace, dan kan na verbinding cb, bd, cd worden gezocht de lengte van de Komeet in e, en de breedte ec op de volgende manieren. 