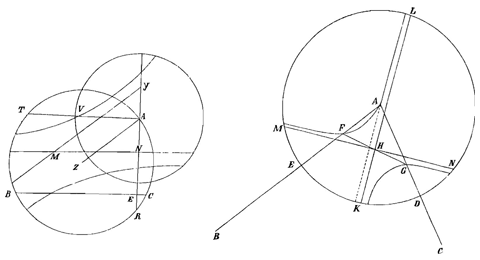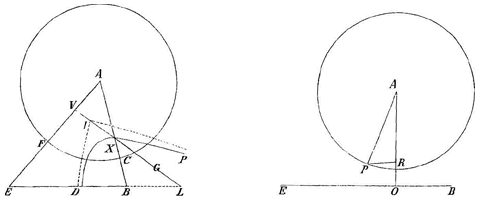Als u bij gelegenheid mij een monster van het glas van Lambeth 5) zou kunnen sturen, zoals u zo goed bent me aan te bieden, zou ik er zeer blij mee zijn, want doordat ik hier geen behoorlijke grondstof kon vinden, heb ik het werk laten stopzetten.
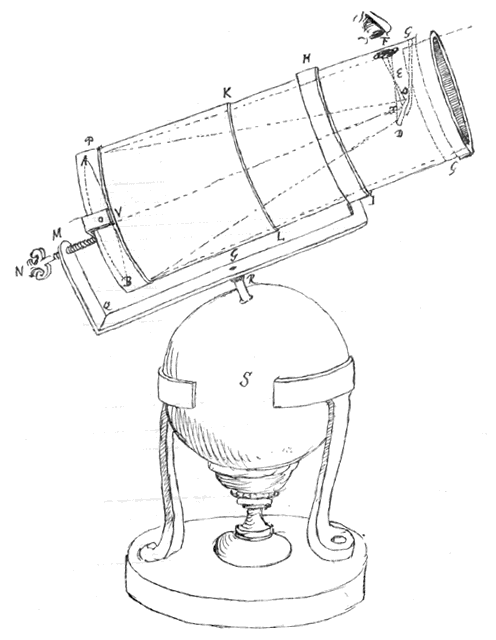
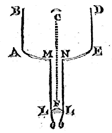
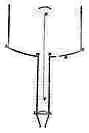
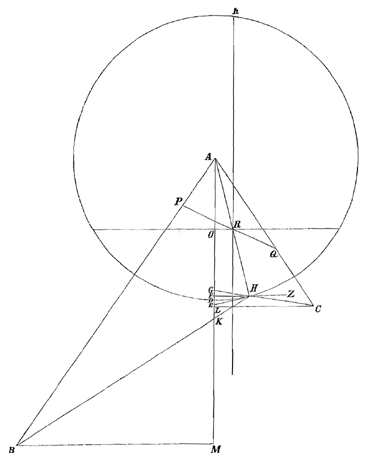
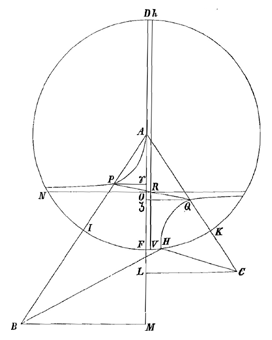
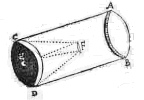
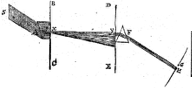
Ik heb het toestel van meneer Wren 6) heel goed bekeken en ik geloof dat men door middel daarvan hyperbolische glazen zou kunnen slijpen, maar dat het lastig zou zijn ze een voldoend nauwkeurige vorm te geven om te dienen als objectieven voor verrekijkers, wetend welke perfectie daarvoor vereist is door de moeilijkheid die men heeft bolvormige glazen te maken, waarvan de vorm zo voordelig is in het werk. Ik weet niet wat hij heeft gevonden door het te proberen, maar ik twijfel eraan of men alleen al een glas goed kan polijsten dat slechts op een lijn tegen de vorm raakt, zoals zijn hyperbool wordt gemaakt. Overigens lijkt me de theorie van die 2 klossen, die elkaar perfectioneren echt heel vernuftig en subtiel.
Het boek van de heer Wallis is nog niet aangekomen 7) naar wat de heer Justel mij 2 dagen geleden heeft gezegd. Hij heeft me de kleine verhandeling van meneer Boyle 8) geleend over absolute rust, met wiens mening ik geen moeite had het eens te zijn, omdat ik al dezelfde had. Alleen zou ik niet geheel durven vertrouwen op wat hij
3) Zie het stuk No. 1745. [<]
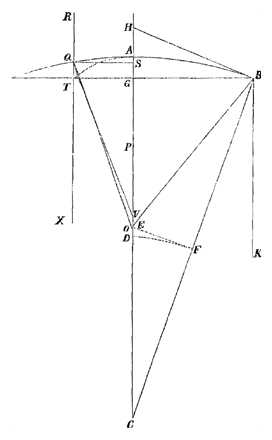
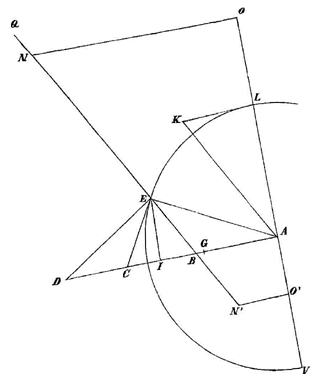
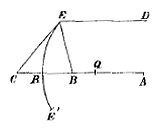
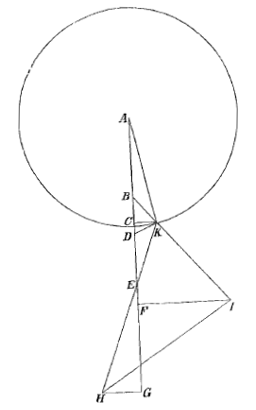
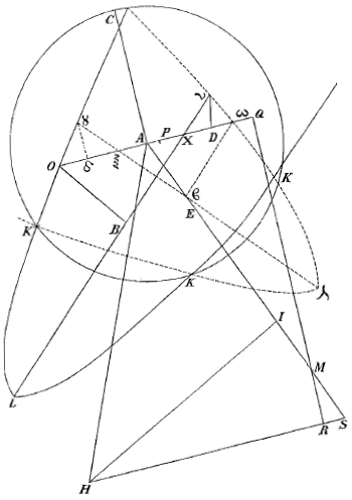
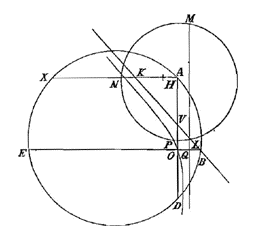
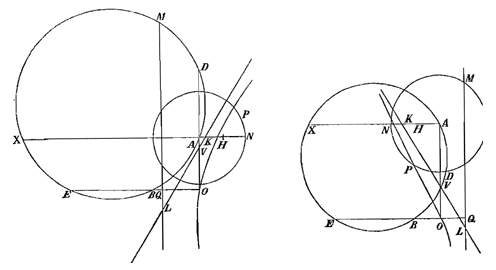
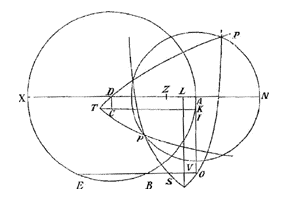
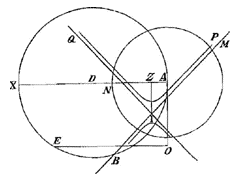
4) In § XII van Lectio IX geeft Barrow een constructie van het weerkaatste beeld van een lichtpunt in een bolle spiegel [fig. 95-6]. Hij begaat de fout de plaats van samenkomst van schuine stralen te zien als de precieze plaats waar een toeschouwer, die zich bevindt in de richting van de teruggekaatste schuine stralen, het beeld zou zetten [zie T. XIII, 777; noot 25 op p. 775 begint met de 'moeilijkheid' aan het eind].
5) Zie No. 1779, n. 5.
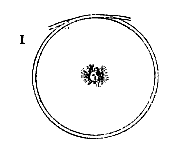
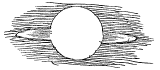
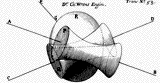 6) Zie Phil. Tr. Numb. 48 (June 21 [fig. 1]) en Numb. 53 (Nov. 15, 1669) [fig. rechts. 'Hyperbolical Cylindroid', ms.].
6) Zie Phil. Tr. Numb. 48 (June 21 [fig. 1]) en Numb. 53 (Nov. 15, 1669) [fig. rechts. 'Hyperbolical Cylindroid', ms.]. 7) Het eerste deel van Mechanica sive de motu. Zie brief No. 1792, noot 4.
8) Certain physiological essayes and other tracts ... The second edition. Wherein some of the tracts are enlarged by experiments, and the work is increased by the addition of a Discourse about the absolute rest in bodies. London, 1669.
[Add. T. X, p. 811:] In dit werk wil Boyle bewijzen dat niets ons verhindert te veronderstellen dat zelfs in de hardste lichamen de deeltjes voortdurend in beweging zijn.
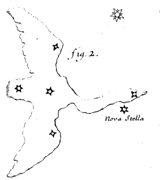


 [ *) In Ms. UB Leiden HUG 5, 50v: waarneming van Saturnus, 6 nov. 1671.]
[ *) In Ms. UB Leiden HUG 5, 50v: waarneming van Saturnus, 6 nov. 1671.]