Overzicht , Inleiding , taal , water , wet van Archimedes , paradox , kracht op wand , mens
Stevins Waterwicht
Het 'Waterwicht' heeft 63 blz, hier verdeeld in stukken van zo'n 10 blz.
Byvough der Weeghconst (1605): Vlietende Topswaerheyt, over evenwicht van een schip.
Zie deel 1 van Principal Works voor een facsimile.
InleidingAnghesien kennelick ghenouch is, E. Heeren, de gheduerighe oefning die dese landen mettet water hebben, meer als ander; waer in oock blijckelick is, wat grooter voordeel hun de oirsaeckelicke kennis der wichtighe ghedaenten des waters doen can; ghemerckt daerbeneven dat onse Weeghconst die duer d'uyterste beghinselen openbaertDe theorie staat weer in dienst van de praktijk: spiegeling en daad zijn allebei nodig. Inzicht in de gewichts-eigenschappen van water geeft voordelen, zoals: kunnen berekenen hoe zwaar je een schip kunt beladen, en: hoe hard water drukt tegen een sluisdeur. TaalWat beweeghlicke oirsaeck Archimedes had, om te schrijven t'ghene hy ons in t'Bouck vande dinghen die int water ghedreghen worden {Lib. de iis quæ vehuntur in aqua.}, naghelaten heeft; daer hy de natuer heerlick begon te treffen, en weet ick niet; maer wel dit, dat hy de myne gheweest is [...]Stevin laat zien dat moeizame formuleringen na "ouersetting" in onze taal veel korter en duidelijker zijn. Hij citeert twee stukken uit Commandino's Latijnse vertaling (1566) van de "Keghelsche boucken" van Apollonius, die "wy dencken int Duytsch te laten uytgaen" (dit is nooit verschenen). Na vertaling zijn ze vier keer zo kort en veel helderder (als je de termen kent). In plaats van spot zien we dan: "diens naem ick met eerbieding gheern ghedenck", en "duer wiens neersticheyt veel saken die int Griecx verborghen laghen, anden dach ghebrocht sijn". De kortere formulering is te danken aan de "helpende oirsaec" die Stevin had in zijn taal. Soo ist mettet Duytsch ghestelt, ende diets hem niet en verstaet, bidt hem, beminde leser, dat hijt leere, lieuer dan als een dwaes van het Duytsch dwaeslick te oirdeelen. Watertottet einde, dat is de Waterwichtdaet, niet voorderlicker, soo worter begheert datmen toelate, yder waters oppervlack plat te wesen, euewydich vanden sichteinder.Andere uitzonderingen zijn te vinden in een droppel erghens op ligghende ofte anhangende, ofte in water daer eenich lichaem me bestreken mocht wesen [...]Water rust op water, anders zou er een "eewich roersel" zijn. Voorstel 1 zegt het zo: T'ghestelde water houdt alle plaets diemen hem binnen water gheeft.Op blz 16 blijkt de "form soot valt" in de tekening een schip te zijn, en dat ligt in een water van t'welck een teerlincksche voet [kubieke voet] weeght 65Zeewater is anders: Laet by voorbeelt een schip ligghen inden Rhijn te Leyen, ende men wil weten hoe veel dattet daerin dieper sincken sal dan in See voor Catwyck. Men sal ondersoucken de reden der stofswaerheyt van dat water tot dit, welcke sy als van 42 tot 43, soo heb ickse in Hoymaent duer d'eruaring beuonden, want nemende twee euegroote lichamen, dat vanden Rhijn wouch 4260 azen maer t'Seewater 4362 azenStevin kon nauwkeurig wegen: zijn verhouding is 1,024 en die vinden we ook in een tabellenboek (bij 20 °C en 3 % zout). Hij gebruikte minder dan een half pond water. De temperatuur kon hij niet opgeven, een 'Warmtekunde' was er nog niet. Maar het was wel een warme zomermaand. WetHet genoemde 'vlackvat' is een denkbeeldig vat sonder lichamelicke grootheyt, ende sonder ghewicht [...]Zie ook: Bepaling 7, en Begheerten 4, 5. De 'lichtheid' kan ook gemeten worden: voor het "staltwicht in t'water" wordt een katrol onder water getekend. Een uitbreiding van de wet staat in de Anhang: so neemt dat een man gantsch onder t'water sy, aldaer by hem hebbende quicsiluer, gout, met een waegh, ende houdende t'water als voor locht: Ick seg dattet gaudt aldaer so veel lichter sal sijn int quicsiluer dan int water, als de swaerheyt des quicsiluers mettet gaudt euegroot ParadoxWaer uyt blijckt dat eenighe drijuende stof in t'water gheleyt, sy en verswaert noch en verlicht (welverstaende als t'water inde selfde hoochde blijft) den grondt niet.Een mooi betoog leidt in Voorstel 10 tot de hydrostatische paradox, die eigenlijk zou moeten heten 'paradox van Stevin' (zie Devreese): dat den bodem des waters [...] duer een grooter water (d'hoochde de selfde blijuende) niet meer beswaert en wort dan duer een cleinderDeze formulering komt uit de Waterwichtdaet, en daar staan heuse natuurkundeproeven 1, want den menighen dat voor onnatuerlick mocht achten, sullen bouen t'voorgaende Wisconstich bewys, daeraf vijf daetlicke voorbeelden beschrijuen, welcke yghelijck versoucken, ende ooghenschijnlick sien mach. 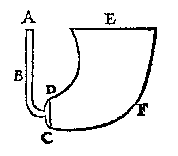 Voorbeeld 2: Een "cleen dun buysken" en een "groot dick vat" (zie figuur); en bij 4 is de conclusie:
Voorbeeld 2: Een "cleen dun buysken" en een "groot dick vat" (zie figuur); en bij 4 is de conclusie:
dat I lb waters [...] meer ghewelts sal connen doen [ ... ] dan hondert duysent ponden [ ... ], t'welckmen der naturen verborghenheyt soude mueghen noemen dat d'oirsaken onbekent waren. Geprang tegen de wand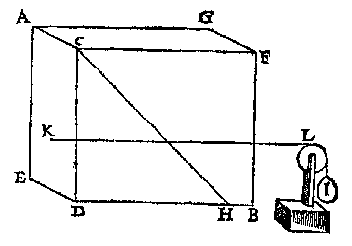 Voorstel 11 gaat over de kracht van het water tegen de wand ("helft des pilaers waters", DH = DC). Het 'begheerde' geeft een vooruitblik naar voorstel 18: waar grijpt de kracht aan?
Voorstel 11 gaat over de kracht van het water tegen de wand ("helft des pilaers waters", DH = DC). Het 'begheerde' geeft een vooruitblik naar voorstel 18: waar grijpt de kracht aan? (de tekening is vereenvoudigd)
Het probleem wordt goed inzichtelijk gemaakt door kantelen (AC wordt MP) en een 'stijflichaem' in plaats van water:
alsulcken gheprang [...], te weten meer pranghende naer NO dan naer MP, om dattet aldaer dicker en swaerder is dan alhierHierna volgt een lang bewijs voor de stelling dat de "macht des gheprangs" gelijk is aan het gewicht aan water van het getekende prisma 2. De methode van de "oneindelicke naerdering" wordt nog verduidelijkt met een rekenvoorbeeld: de wand (bodem) wordt verdeeld in gelijke horizontale stukken; eerst vier, dan "in soo veel deelen alst ons belieft, latet sijn in thienen", en dan voor alle zekerheid: "deelende den bodem duer de ghedacht in 1000 euen deelen". In de Waterwichtdaet blijkt het belang van deze stelling: daer uyt is onder anderen kennelick, wat ghewicht waters datter druct, teghen elcke siide der duer van een sluys, ende dierghelijcke: Oock dattet water ouer d'een siide alleenlick een stroobreet, daer teghen soo stijf prangt als t'water diens breede de Zee van Oceane ouer d'ander siide; Welverstaende als sy euenhooghe siin.Met deze kennis heeft Stevin een nieuw ontwerp gemaakt voor een watermolen. En dit inzicht van het verschil tussen 'macht' en 'geprang' was ook toepasbaar op een ander gebied: dat van de vestingbouwkunde. In de Sterctenbouwing vinden we, na beschouwingen over "overwelfsels van kelders, brugghen, kercken" en over een "bornput", de opmerking: soo der bolwercken ghebruijck inhielde, te moeten wederstaen een persinghe die van buijten over al daer teghen anquaem, soo soude de veelhouckighe, of ronde form tot dien einde wel stercker wesen, maer sulcke persinghe en worter niet op verwacht. Angaende de clooten die van buijten daer op gheschoten worden, dat en is gheen persinghe overalDit is een duidelijk voorbeeld van wat 'spiegeling en daad' vermag: een algemeen theoretisch inzicht biedt oplossingen voor heel diverse praktische problemen. DuikenLaet een mensch 20 voeten diep onder water ligghen, weghende elcke voet waters 65 lb, ende t'gheheel vlack sijns lichaems sy groot 10 [vierkante] voeten. Dit soo wesende, daer sal teghen sijn lijf perssen byde 13000 ponden ghewichts [...]Met een 'syllogisme' bewijst Stevin dat je heel blijft: A. Alle duwing die t'lichaem weedom andoet, verset eenich deel des lichaems uyt siin natuerlicke plaets ;En hij licht toe: Soo eenich deel als vleesch, bloet, vochticheyt, wattet sy, uyt sijn natuerlicke plaets verset wierde, t'soude moeten plaets hebben daert in ghinge, die plaets en is buyten t'lichaem niet, [...] sy en is oock binnen t'lichaem niet, wanttet [omdat het] daer soo vol lichamelickheyts is als daer buyten, waer duer yder dit deel, soo stijf stoot teghen yder dat deel, als yder dat, teghen yder dit, ouermits t'water rondom t'lichaem tot allen sijden met een selue reden staat. 3 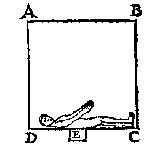 Zou Stevin ook gedacht hebben aan ingeademde lucht?
Zou Stevin ook gedacht hebben aan ingeademde lucht?Nog een gedachtenproef: Maer wildi nu daetlick sien dit de waerachtighe oirsaeck te wesen, so trect den tap E uyt, ende dan en sal teghen sijn rug an E gheen stootsel sijn, als an alle d'ander plaetsen sijns lichaems, daerom oock sal het lichaem daer prangsel lijden, ende dat soo stijf [ ... ] als veroirsaeckt wort duer t'ghewicht des pilaers waters, diens gront het gat E is, ende hoochde, de hoochde des waters bouen hem, waermede t'voornemen opentlick bewesen is. Noten |
 T'vlackvat D vol waters, en is in t'water BC licht noch swaer, want het daer in alle ghestalt houdt diemen hem gheeft, duer het
T'vlackvat D vol waters, en is in t'water BC licht noch swaer, want het daer in alle ghestalt houdt diemen hem gheeft, duer het