Over de experimenten van de illustere Boyle was ik een jaar geleden 3) ingelicht uit Engeland door een weledele heer 4), met mij bevriend, die me onlangs daarover ook mijn mening vroeg, en die vermeldde dat er velen zijn die ze tegenspraken. Maar ik heb een sterk voorbeeld voor de waarheid ervan, omdat ik begrijp dat ze u bevallen. Ondertussen staat het boek 5) hier nog niet te koop, wat de slechte smaak van onze drukkers tekent. Daarom heb ik u gevraagd, u zult het wel goedvinden, via onze heer Vanderveken 6) waar het te koop is, ik heb hem namelijk verzocht het op uw aanwijzing zo snel mogelijk voor mij te kopen.
Mijn studies kwijnen, zoals gewoonlijk; behalve namelijk dat ik die futiliteiten van mij over oneindig veel oplossingen 7) op papier heb gezet, is door mij niets gepresteerd, althans wat ik voor u van betekenis acht. Onlangs heb ik echter een methode voor raaklijnen 8) volgens een of andere bekende manier van ordinaten naar de kant van de as, die ik vele jaren geleden had gevonden, zo makkelijk mogelijk gemaakt, zodanig dat ik, met alleen het bekijken in analytische termen van de vergelijking die de eigenschap van de kromme laat zien, bijna zonder berekening de raaklijn trek. Ik voeg er één bij die met mijn methode gevonden is, aan een kromme die de geleerde van Gutschoven mij lang geleden heeft voorgelegd.
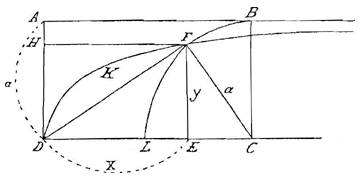
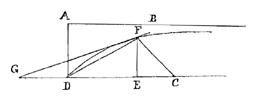 Tussen de evenwijdige lijnen AB en DC, verbonden met de normaal AD, moet men zich een kromme DF voorstellen van een zodanige aard dat, genomen een willekeurig punt F erop, en D met F verbonden, als daarop in F de normaal FC wordt opgericht die DC in C ontmoet, de rechte FC altijd gelijk is aan AD.
Tussen de evenwijdige lijnen AB en DC, verbonden met de normaal AD, moet men zich een kromme DF voorstellen van een zodanige aard dat, genomen een willekeurig punt F erop, en D met F verbonden, als daarop in F de normaal FC wordt opgericht die DC in C ontmoet, de rechte FC altijd gelijk is aan AD.
Uit deze beschrijving blijkt dat AB een Asymptoot van de kromme zal zijn. En een raaklijk in een gegeven punt zoals F wordt gemakkelijk verkregen, wanneer namelijk de normaal FE is neergelaten, en CD verlengd tot G, zodanig dat de drie CE, CD en CG continu evenredig zijn, zal de verbindingslijn GF aan de kromme raken.
En de constructie zal niet veel bewerkelijker zijn bij een andere dergelijke kromme, te weten waarbij de hoek DFC niet recht zou worden verondersteld, maar een willekeurige andere wordt gegeven. Maar deze dingen zijn van weinig belang en
2) Deze brief is niet gevonden.
3) De proeven van Boyle met de luchtpomp waren inderdaad al in 1660 bekend.
4) Waarschijnlijk Sir Richard Towneley, wonend in Towneley, leerling van Boyle, de enige Engelsman die toen met de Sluse in verbinding stond.
5) Waarschijnlijk het boek van brief No. 873, n.4. [Nova experimenta physico-mechanica de vi aeris elastica et ejusdem effectibus, Oxonii 1661 in-12o en Den Haag, 1661, plaat.]
6) Zie brief No. 643, n.4 [Van der Veecken]. 7) Zie brief No. 663.
8) Het is de eerste keer dat deze raaklijnmethode wordt genoemd; ze leidde tot een briefwisseling.

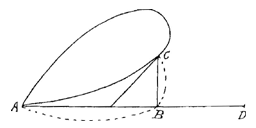
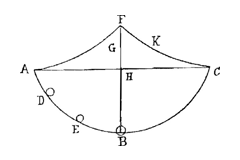 Als over een oppervlak, gebogen volgens de holte van een cycloïde, zoals hier ABC, zodanig dat de as BH een loodrechte stand heeft, als zeg ik een beweeglijk voorwerp daarlangs afdaalt, zal het in dezelfde tijd in het onderste punt B aankomen, uit welk punt van de cycloïde, zoals E of D of A, het ook was losgelaten.
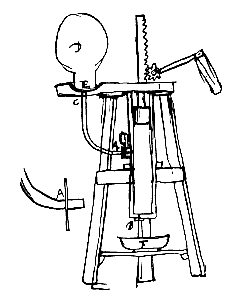
Als over een oppervlak, gebogen volgens de holte van een cycloïde, zoals hier ABC, zodanig dat de as BH een loodrechte stand heeft, als zeg ik een beweeglijk voorwerp daarlangs afdaalt, zal het in dezelfde tijd in het onderste punt B aankomen, uit welk punt van de cycloïde, zoals E of D of A, het ook was losgelaten. 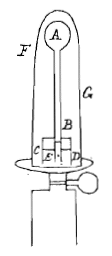 AE is een glazen flesje met langwerpige hals; het is vol met water en met het open uiteinde ondergedompeld in een bakje halfvol water, en hier overheen geplaatst is het grotere glazen vat FG, ongeveer een voet hoog. Wat er dan gebeurt is dat, na uittrekken van de lucht uit het vat FG, het water uit het omgekeerde flesje in het bakje eronder zakt, zo ver dat het water binnen de hals van het flesje bijna op gelijke hoogte blijft staan met dat erbuiten, in elk geval als de luchtpomp goed werkt.
AE is een glazen flesje met langwerpige hals; het is vol met water en met het open uiteinde ondergedompeld in een bakje halfvol water, en hier overheen geplaatst is het grotere glazen vat FG, ongeveer een voet hoog. Wat er dan gebeurt is dat, na uittrekken van de lucht uit het vat FG, het water uit het omgekeerde flesje in het bakje eronder zakt, zo ver dat het water binnen de hals van het flesje bijna op gelijke hoogte blijft staan met dat erbuiten, in elk geval als de luchtpomp goed werkt. 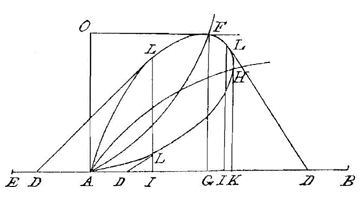
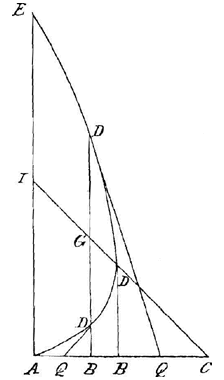 Er zijn er twee bij de rechten EA en AC, waarvan de laatste de helft is van de ander, en daarbij is de kromme ADDE, waarvan de eigenschap is dat bij een willekeurige ordinaat evenwijdig met EA, neem DDB, als AB y wordt genoemd, BD x en AC n, altijd geldt:
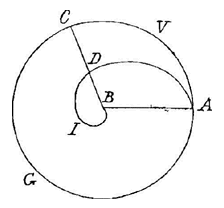
Er zijn er twee bij de rechten EA en AC, waarvan de laatste de helft is van de ander, en daarbij is de kromme ADDE, waarvan de eigenschap is dat bij een willekeurige ordinaat evenwijdig met EA, neem DDB, als AB y wordt genoemd, BD x en AC n, altijd geldt: 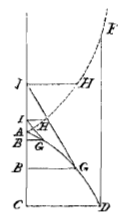 Gegeven zij een of andere kromme AGD, waarvan de as AC is, in de richting van A oneindig verlengd, de ordinaat CD, een willekeurige raaklijn GI die de as ontmoet in I, en vanuit het punt G de ordinaat GB.
Gegeven zij een of andere kromme AGD, waarvan de as AC is, in de richting van A oneindig verlengd, de ordinaat CD, een willekeurige raaklijn GI die de as ontmoet in I, en vanuit het punt G de ordinaat GB.